0 引 言
我国西部浅埋煤层赋存条件优越,但由于其特殊的地质赋存条件,煤层开采后覆岩运动呈现出与常规埋深煤层不同的特征。多年来,国内学者针对浅埋煤层开采条件下覆岩结构及岩层控制开展了大量研究[1]。黄庆享等[1-3]针对浅埋煤层开采提出了覆岩“短砌体梁”和“台阶岩梁”结构,浅埋深大采高工作面“短悬臂梁”和“高位斜台阶岩梁”结构,浅埋煤层群的双关键结构模型等。许家林等[4-5]提出了浅埋煤层覆岩结构分为单一关键层和复合关键层2类,得出关键层结构类型的判别方法,并对浅埋深条件下的压架类型进行了研究;李凤仪[6]提出了受采场周期来压影响的“承压砌块”力学模型;侯忠杰[7]提出了浅埋深组合关键层结构,并对其稳定性进行了详细研究。地下煤层开采后的覆岩结构是覆岩破断和运移的结果,实质是煤层开采后围岩应力重新分布特征的表现,因此针对围岩应力结构的分析可以加深对覆岩结构研究的认识。在浅埋深围岩应力场研究方面,谢广祥等[8]研究了浅埋煤层回采过程中采场围岩力链的演化特征,认为强力链拱是承载采场上方煤岩体重力的主要力系,其失稳断裂是工作面产生强动载现象的原因。任艳芳等[9-11]提出了浅埋深条件下的承压拱结构,认为采高及工作面长度对其稳定性有影响。以上关于浅埋深围岩应力场的研究成果对覆岩结构研究提供了思路,但仍存在一些不足。笔者以浅埋深长壁采场围岩应力结构特征为研究对象,借助三维数值模拟手段,从围岩应力场分布规律入手,对浅埋深条件下围岩应力结构特征进行分析,并对其在覆岩中的力学作用及存在形式进行研究。
1 数值模型建立与参数确定
采用FLAC3D软件模拟浅埋深长壁工作面的回采过程,分析工作面围岩应力结构特征与演化规律。
1.1 数值模型建立
纳林庙煤矿位于鄂尔多斯市准格尔旗羊市塔乡,主采6号煤层,平均厚度6 m;埋深76~104 m,平均88 m;地表覆盖层主要是黄土,平均厚度10 m,基岩层平均厚度78 m,属于典型的浅埋煤层开采。严格按照顶底板柱状图建立数值模型,如图1所示。模型长×宽×高为190 m×300 m×110 m,模型前后左右及底部固定位移。模型内布置有区段巷道和开切眼,首先进行区段巷道与开切眼的开挖模拟,然后进行工作面回采模拟。模拟工作面倾向长度为240 m。
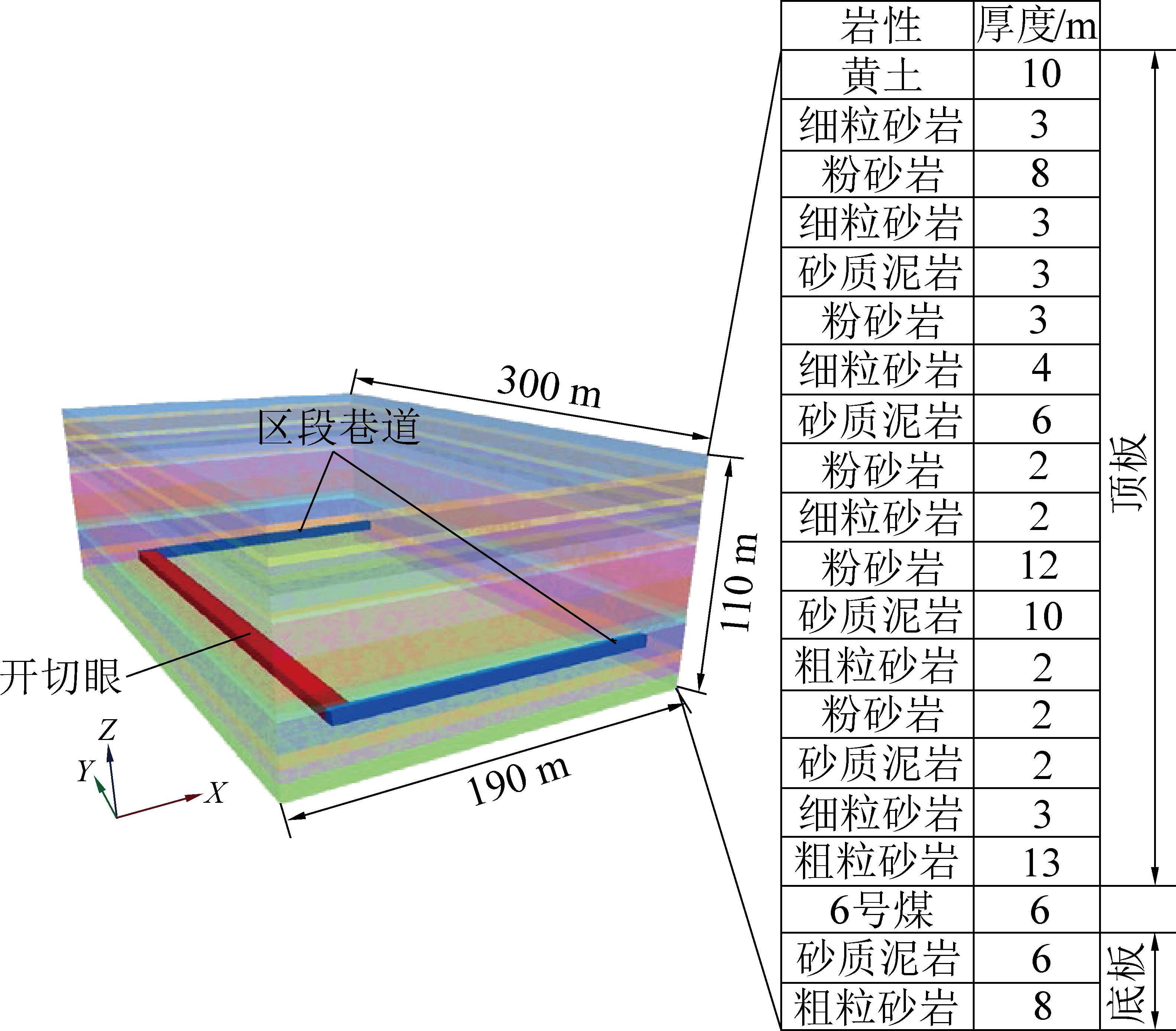
图1 数值模型
Fig.1 Simulation model
1.2 模拟参数确定
1)参数确定方法。数值模型中岩体力学参数确定是进行数值模拟的关键和难题。在采矿工程领域,基于FLAC3D的数值模拟通常采用Mohr-Coulomb强度准则作为本构模型,但由于岩体与岩块力学性质的巨大差别,岩块参数并不能直接应用于岩体[12]。为此,Hoek E和Brown E T通过大量的三轴试验,从其强度拟合曲线上总结提出Hoek-Brown 经验准则[13],如式(1)所示:
σ1=σ3+σc(mbσ3/σc+s0)a
(1)
其中:mb为岩体折减参数;s0(0≤s0≤1)为岩石破碎程度参数;a为与岩体质量有关的参数;σ1和σ3分别为最大主应力和最小主应力;σc为岩石的单轴抗压强度。Hoek-Brown强度准则中的经验参数可通过地质强度指标GSI(Geological Strength Index)确定[14-18]。
2)参数确定过程。对纳林庙煤矿6号煤层顶底板岩层进行现场取样并开展实验室试验,获得各类岩体标准煤岩样的力学指标,见表1。根据纳林庙煤矿钻孔岩心取样成果,结合GSI岩体强度指标体系[19]和表1数据结果,确定岩体的地质强度指标GSI,反映完整岩石软硬程度的参数 mi,岩体的受扰动程度参数D(0≤D≤1) [18]。通过计算得到各类岩体的力学参数,见表2。对比表1与表2可知,采用Hoek-Brown准则确定岩体强度参数的方法考虑了岩体结构面及赋存等相关地质因素,应用更加科学。
表1 标准煤岩样力学参数
Table 1 Mechanical parameters of standard coal and rock samples
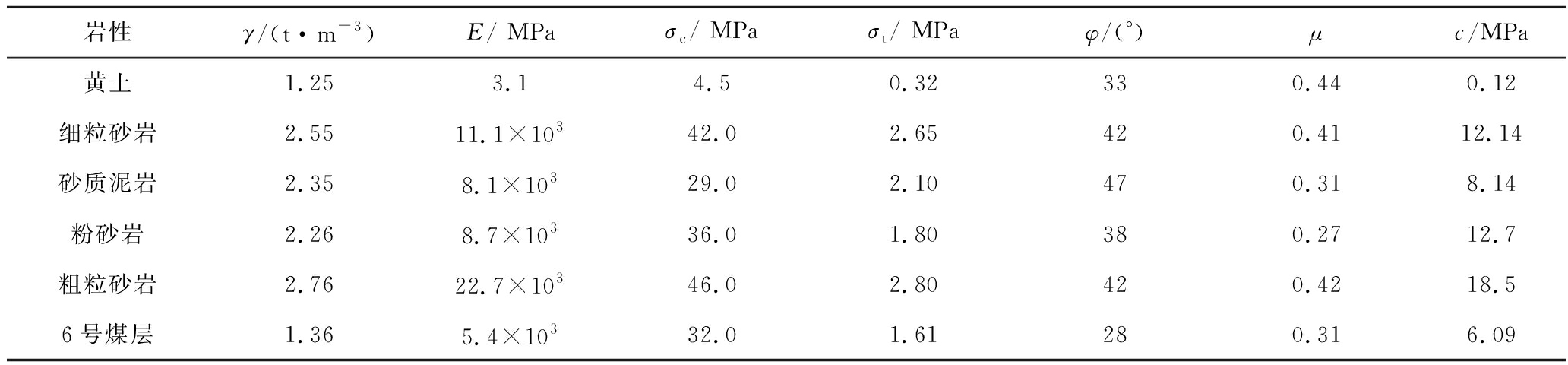
岩性γ/(t·m-3)E/ MPaσc/ MPaσt/ MPaφ/(°)μc/MPa黄土1.253.14.50.32330.440.12细粒砂岩2.5511.1×10342.02.65420.4112.14砂质泥岩2.358.1×10329.02.10470.318.14粉砂岩2.268.7×10336.01.80380.2712.7粗粒砂岩2.7622.7×10346.02.80420.4218.56号煤层1.365.4×10332.01.61280.316.09
注:γ为岩石容重;E为岩石弹性模量;σt为岩石抗拉强度;φ为岩石内摩擦角;μ为岩石泊松比;c为岩石黏聚力。
表2 基于Hoek-Brown强度准则确定的岩体参数
Table 2 Rock parameters determined by Hoek-Brown strength criterion
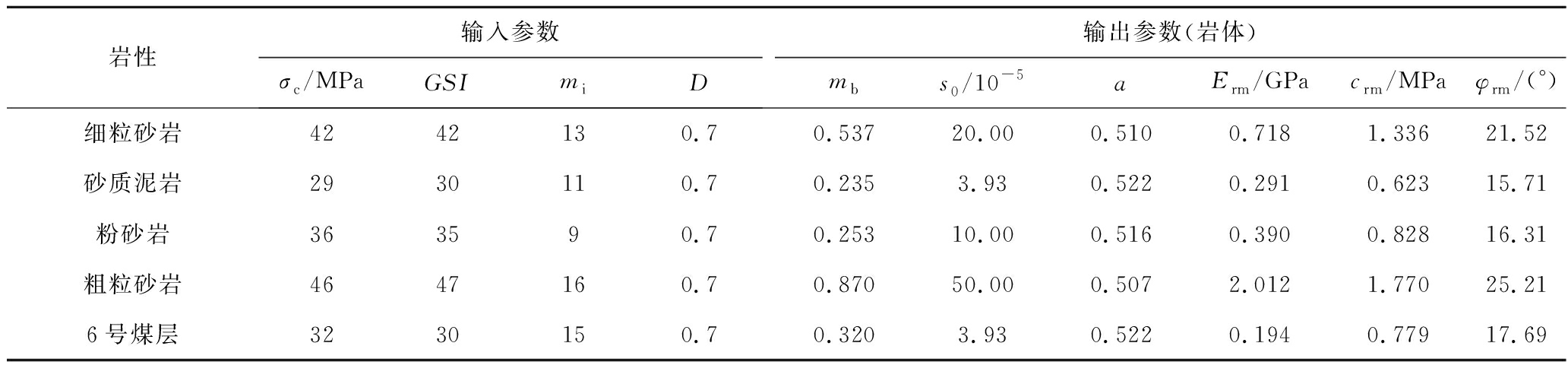
岩性输入参数σc/MPaGSImiD输出参数(岩体)mbs0/10-5aErm/GPacrm/MPaφrm/(°)细粒砂岩4242130.70.53720.000.5100.7181.33621.52砂质泥岩2930110.70.2353.930.5220.2910.62315.71粉砂岩363590.70.25310.000.5160.3900.82816.31粗粒砂岩4647160.70.87050.000.5072.0121.77025.216号煤层3230150.70.3203.930.5220.1940.77917.69
注:Erm为岩体弹性模量;crm为岩体黏聚力;φrm为岩体内摩擦角。
2 围岩应力结构特征分析
2.1 承压拱结构的形成与演化
浅埋煤层开采后造成上覆岩层破坏和围岩应力的重新分布。图2为工作面推进距离为20 m时,围岩最大主应力矢量线沿工作面走向和倾向的分布情况。可以看出,工作面围岩中最大主应力在回采空间周边区域形成了类椭球体应力集中带,在沿工作面走向与倾向方向上,均呈现为拱状应力承载结构——承压拱。
工作面推进20 m时,承压拱结构在沿工作面走向的基本形态参数如图3a所示。分析图3a可知,承压拱内的应力明显高于其他区域。沿工作面走向,承压拱结构上部的厚度为4.4 m,承压拱内壁距离直接顶下边缘5.1 m(结合岩层柱状图,此位置为顶板粗粒砂岩);应力峰值点分别位于煤层上方8 m处与煤层下方9.8 m处,应力分别为2.72、3.30 MPa;承压拱侧向厚度约为6.7 m,应力峰值点位于煤体内3 m处,应力为4.06 MPa。

图2 工作面推进20 m围岩中最大主应力矢量线分布
Fig.2 Vector distribution of maximum principal stress in
surrounding rock when working face advancing 20 m
随着工作面推进,承压拱在高度和宽度方向不断发展变化,当工作面推进至50 m时,基本顶发生初次垮落,如图3b所示。

图3 工作面不同推进长度时承压拱形态演化
Fig.3 Form evolution of pressure bearing arch with
different working face advancing length
随着工作面的推进,顶板岩层逐渐下沉破坏,以工作面前后方煤体为支承的承压拱结构不断发展变化,承压拱的高度、跨距均逐渐增大。同时,承压拱内的应力仍然明显高于其内、外部岩体的应力,依旧是稳定的承载结构。
2.2 承压拱结构的失稳与再形成
当工作面推进至100 m时,工作面上覆岩层的破坏情况和应力分布如图4所示。

图4 工作面推进100 m覆岩状态
Fig.4 Overburden state of working face when advancing 100 m
由图4可知,黄土覆盖层以下的基岩已全部破断,并且顶板岩层中的应力集中带被割裂,不再连续,表明承压拱已失稳破坏。在浅埋煤层中,承压拱的失稳破坏会导致地表覆盖层与基岩层发生同步下沉。
图5为工作面推进120 m时再次形成的承压拱结构。由图5可知,基岩层破断后,在工作面煤壁前方的煤体与采空区压实矸石,采空区压实矸石与开切眼煤壁后方煤体之间会形成新的承压拱结构,二者之间的低应力区域是采空区矸石压实区域。随着工作面继续推进,工作面承压拱在煤壁前方煤体内的支撑基础将被破坏,导致其高度和跨距不断演化,直至其失稳破坏。
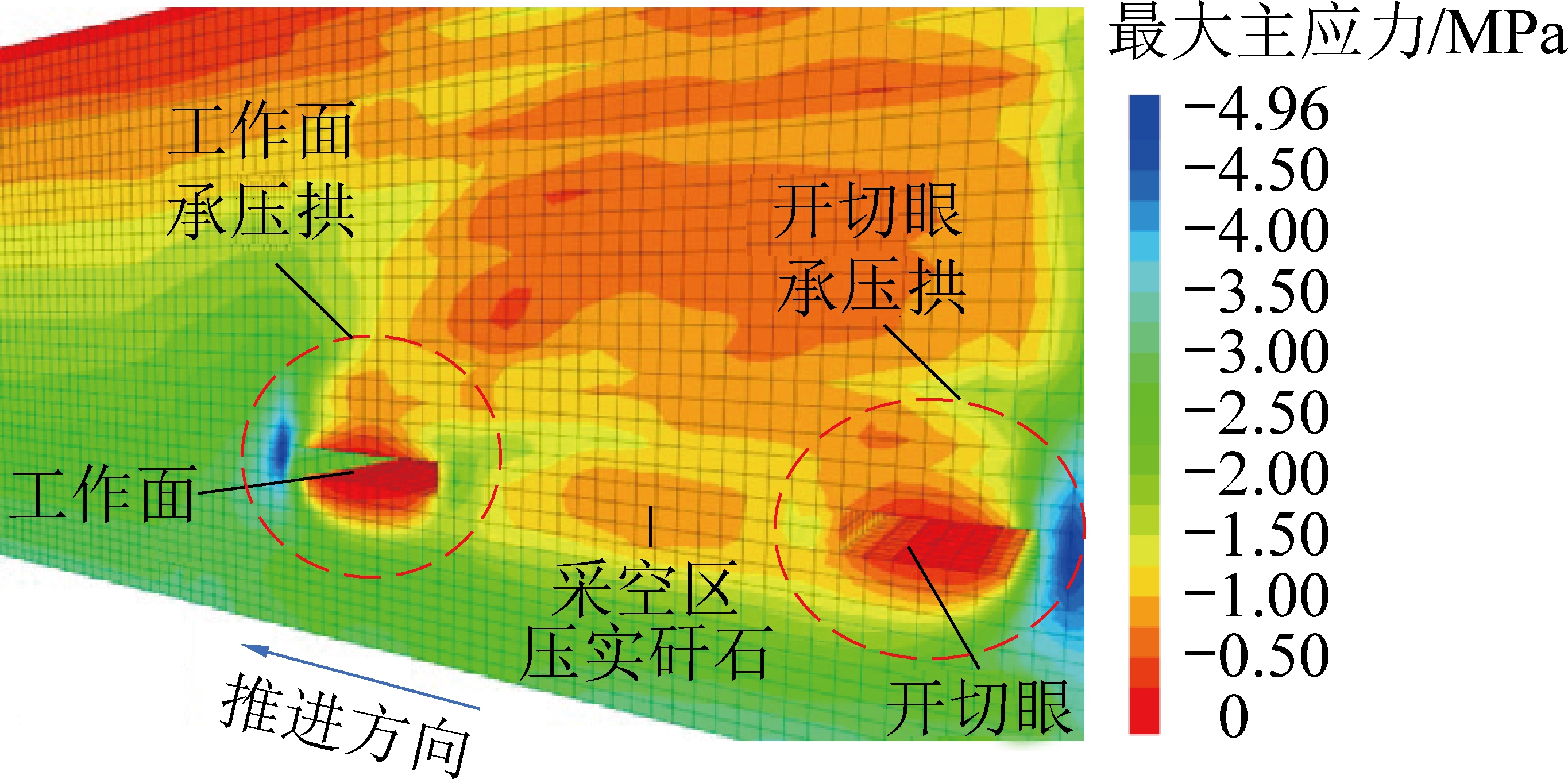
图5 工作面推进120 m承压拱再形成
Fig.5 Reformulation of pressure bearing arch
when working face advancing 120 m
3 承压拱结构的力学分析
3.1 承压拱的形态参数
根据以上分析,承压拱结构剖面上具有拱的特征,其上半部分是影响工作面煤壁及顶板稳定的主要区域,可将该结构简化为以工作面前后方煤岩体为支承的拱状应力承载结构。为便于分析,将浅埋煤层上覆岩层作为平面应变梁,以此建立半无限Winkler弹性地基梁和工作面后方连续梁的挠曲线微分方程[13],简化后的模型如图6所示。

m—煤层上方岩梁层数量;x—第m层岩梁截面沿走
向相对工作面煤壁的距离;y—第m层岩梁截面竖向位移
图6 采场覆岩结构的基础力学模型
Fig.6 Foundation mechanical model of
overburden structure on working face
根据已有成果,承压拱的迹线即各岩层弯矩为零的连接线,因此以承压拱迹线上弯矩M=0作为判据,分析承压拱结构在特定状态下的拱脚位置及其主要结构形态参数。
在工作面煤壁上方顶板第m层岩梁建立笛卡尔坐标系(x,y),如图6所示。工作面的某一推进阶段中,顶板第m层岩梁的弯曲变形微分方程为
EIy‴′+Nmy″+ky=0
(2)
式中:k为Winkler综合地基系数;EI为抗弯刚度;Nm为工作面煤壁位置(x=0)顶板第m层岩梁截面轴力。
1)对于工作面煤壁前方,其边界条件为:x→ 时,y→0,可求得第m层岩梁工作面前方的竖向位移为
时,y→0,可求得第m层岩梁工作面前方的竖向位移为
![]()
![]()
(3)
式中:M0,m为工作面煤壁位置(x=0)顶板第m层岩梁截面弯矩;Q0,m为工作面煤壁位置(x=0)顶板第m层岩梁截面垂直作用力。
顶板第m层岩梁弯矩M为
![]()
![]()
(4)
顶板第m层岩梁剪力Q为
![]()
![]()
(5)
2)对工作面煤壁后方,利用弹性地基岩梁的连续性可以求得顶板第m层岩梁竖向位移及其对应的弯矩和剪力。
工作面煤壁后方顶板第m层岩梁竖向位移y′为
![]()
![]()
(6)
工作面煤壁后方顶板第m层岩梁弯矩M′为
![]()
![]()
(7)
工作面煤壁后方顶板第m层岩梁剪力Q′为
![]()
![]()
(8)
式中:kk为控顶区的Winkler地基系数。
最大弯矩所在的位置即为顶板第m层岩梁断裂的位置,根据工作面前后方顶板第m层岩梁截面计算公式可知,在Q=0的位置处弯矩M取得最大值,推导得到顶板第m层岩梁的断裂位置至工作面煤壁距离x0为
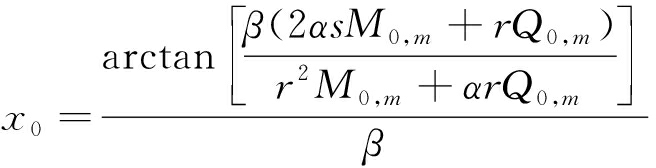
(9)
在浅埋煤层条件下,岩层中的承压拱对工作面的稳定情况起着重要影响,故其极限状态影响着回采工作面的安全。根据已有研究成果可知,承压拱的极限状态是在此拱迹线上弯矩M的值为0,该承压拱仅受到轴向力的作用。
因此,当弯矩M=0时,可得到顶板第m层岩梁至回采工作面煤壁的距离,即承压拱结构在该层岩梁达到极限状态时拱脚至煤壁的距离x1为
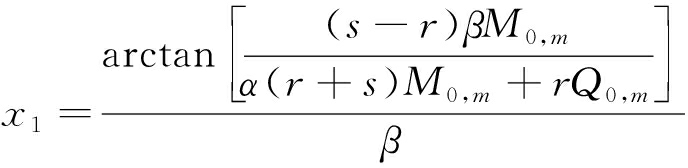
(10)
3.2 承压拱极限拱高和极限跨距
为更方便地说明浅埋深条件下承压拱应力结构的稳定条件,建立的承压拱力学模型如图7所示。
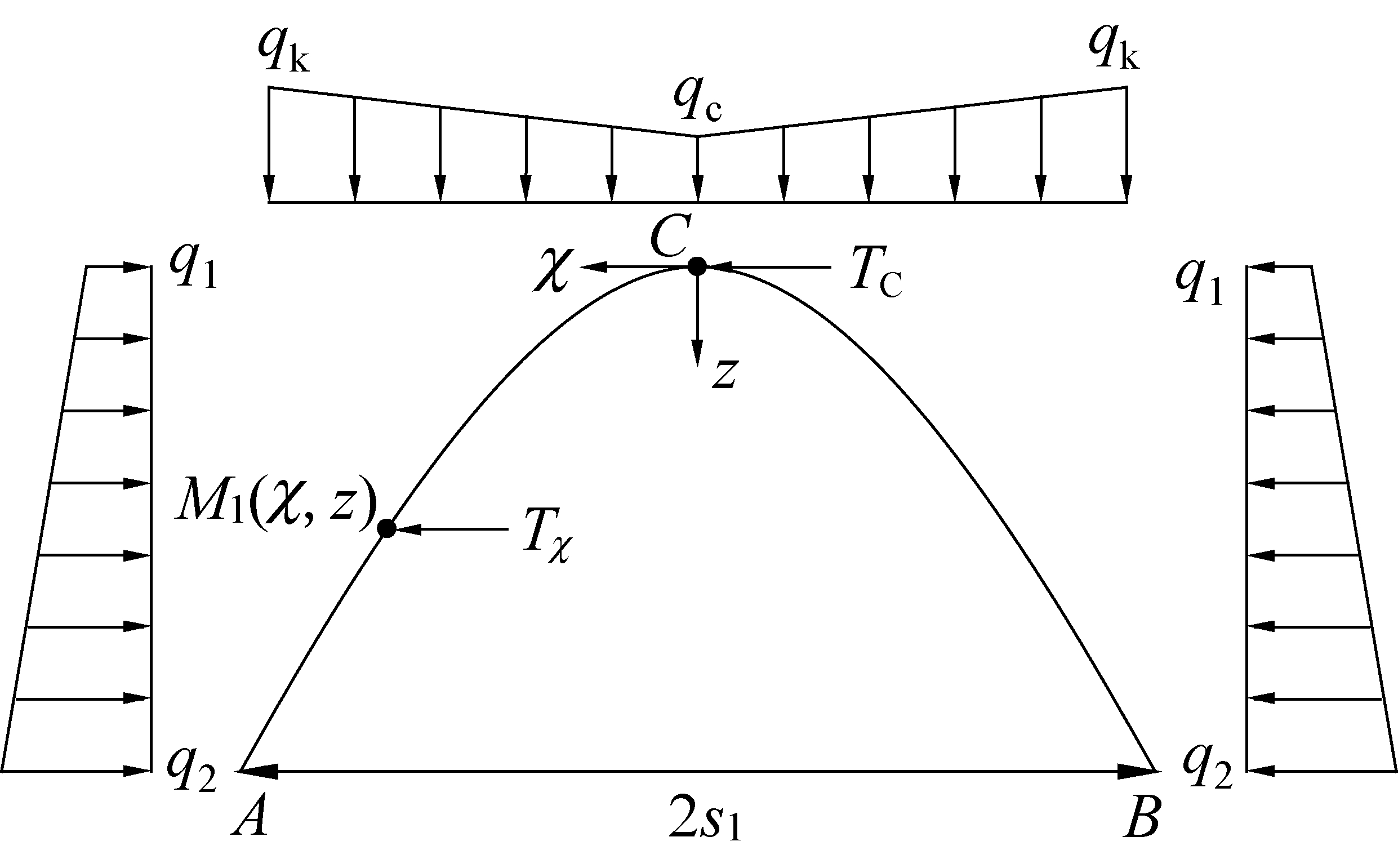
qC—拱顶垂直受力;qk—拱底垂直受力;q1—拱顶
水平受力;q2—拱底水平受力;TC—拱顶C处的轴向力;
s1—承压拱跨距的1/2;
Tχ—任意截面M1(χ,z)处的水平推力
图7 承压拱力学模型
Fig.7 Mechanical model of pressure bearing arch
分析其极限状态下的拱高和跨距,在承压拱拱顶C处建立笛卡尔坐标系(χ,z)。
任意截面M1(χ,z)处的水平推力为
(11)
式中:h为承压拱拱高。
利用极限承压拱在该点处的力矩平衡方程,可以计算出拱顶处的轴向力为
TC=Tχ+s1fq2
(12)
式中:f为煤岩坚固性系数。
推导出承压拱极限拱高计算公式:
(13)
式中:H为承压拱拱顶上覆岩层厚度。
承压拱在不同演化阶段的极限高度和极限跨距对分析浅埋深条件下顶板结构稳定性,研究顶板灾害防治措施具有重要意义。
3.3 承压拱在覆岩中的存在形式
根据承压拱应力状态和承压拱形态参数方程,可得承压拱迹线上任一位置处的力学状态,如图8所示,其后拱脚位于开切眼后方实体煤上。
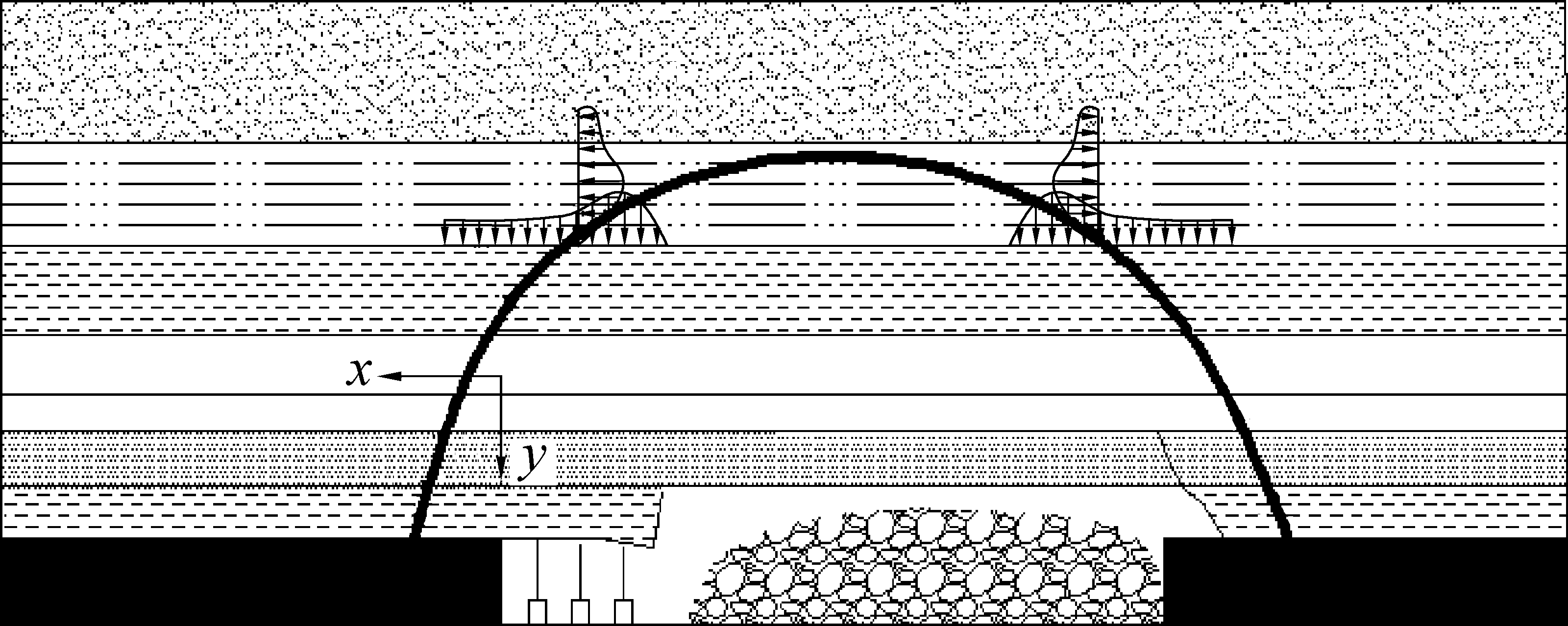
图8 承压拱迹线上的力学状态(初次失稳前)
Fig.8 Stress state on trace of pressure
bearing arch before its first instability
浅埋深条件下,承压拱应力结构发生初次失稳后,其后拱脚前移至采空区压实的矸石上,拱结构形态变化如图9所示。

图9 承压拱迹线上的力学状态(初次失稳后)
Fig.9 Stress state on the trace of pressure
bearing arch after its initial instability
通过分析图9,承压拱应力结构在初次失稳后,随着工作面开采在围岩中继续演化发展,对采场造成影响。结合浅埋深煤层开采后基本顶周期破断及其基岩周期性断裂特征的实践[9],其围岩应力场结构的发展变化规律符合“悬臂梁-铰接岩梁”结构失稳特点[20]。
4 结 论
1)浅埋工作面开采后的采场围岩中形成类椭球体的高应力区域,该应力承载结构形成与失稳是受工作面回采影响的动态演化过程。随着工作面开采,该结构在沿工作面倾向、走向及垂直高度上不断发展变化,直至基岩全部断裂后失稳破坏;初次失稳破坏后,该空间应力承载结构的后方支撑点会迁移至采空区压实矸石上,继续对工作面回采空间提供围岩应力的承载。
2)根据浅埋深工作面围岩应力承载结构的空间形态特征,建立其沿工作面走向的承压拱力学模型,推导出其在覆岩中的形态参数方程和极限状态下的高度及跨距。根据极限承压拱的迹线即各岩层弯矩为零的连接线,得到了承压拱迹线上任一位置处的力学状态。
3)承压拱应力结构在初次失稳后,随着工作面开采在围岩中继续演化发展,对采场造成影响。结合浅埋深煤层开采后,基本顶及其基岩周期性断裂特征的实践,承压拱结构的发展变化规律符合“悬臂梁-铰接岩梁”结构失稳特点。
致谢:在现场数据采集和实验测试分析过程中得到了伊泰集团纳林庙煤矿贺奇良总工程师、中煤科工开采研究院有限公司高晓进硕士和王晓卿硕士的帮助和支持,在此表示衷心的感谢!
[1] 黄庆享,钱鸣高,石平五.浅埋煤层采场老顶周期来压的结构分析[J]. 煤炭学报, 1999, 24(6): 581-585.
HUANG Qingxiang, QIAN Minggao, SHI Pingwu. Structural analysis of main roof stability during periodic weighting in longwaII face[J]. Journal of China Coal Society,1999,24(6):581-585.
[2] 黄庆享,周金龙.浅埋煤层大采高工作面矿压规律及顶板结构研究[J].煤炭学报, 2016, 41(S2): 279-286.
HUANG Qingxiang, ZHOU Jinlong. Roof weighting behavior and roof structure of large mining height longwall face in shallow coal seam[J].Journal of China Coal Society,2016,41(S2):279-286.
[3] 黄庆享,周金龙,马龙涛,等. 近浅埋煤层大采高工作面双关键层结构分析[J].煤炭学报, 2017,42(10): 2504-2510.
HUANG Qingxiang, ZHOU Jinlong, MA Longtao,et al. Double key strata structure analysis of large mining height longwall face in nearly shallow coal seam[J]. Journal of China Coal Society,2017,42(10): 2504-2510.
[4] 许家林,朱卫兵,王晓振,等.浅埋煤层覆岩关键层结构分类[J].煤炭学报,2009,34(7):865-870.
XU Jialin, ZHU Weibing, WANG Xiaozhen, et al. Classification of key strata structure of overlying strata in shallow coal seam[J]. Journal of China Coal Society,2009,34(7):865-870.
[5] 许家林,朱卫兵,鞠金峰.浅埋煤层开采压架类型[J].煤炭学报,2014,39(8):1625-1634.
XU Jialin, ZHU Weibing, JU Jinfeng, et al. Supports crushing types in the longwall mining of shallow seams[J]. Journal of China Coal Society,2014,39(8):1625-1634.
[6] 李凤仪.浅埋煤层长壁开采矿压特点及其安全开采界限研究[D].阜新:辽宁工程技术大学, 2007.
LI Fengyi. Study on ground pressure characteristic of shallow coal seam longwall mining and its safe exploitation demarcation[D]. Fuxin: Liaoning Technical University, 2007.
[7] 侯忠杰.地表厚松散层浅埋煤层组合关键层的稳定性分析[J].煤炭学报,2000,25(2):127-131.
HOU Zhongjie. Analysis of combinatorial key strata stability in shallow coal seam with thick loose bed[J]. Journal of China Coal Society, 2000, 25(2):127-131.
[8] 谢广祥,范 浩,王 磊.浅埋煤层采场围岩力链演化规律及工程应用[J].煤炭学报,2019,44(10):2945-2952.
XIE Guangxiang, FAN Hao, WANG Lei. Evolution law and engineering application of surrounding rock force chain in shallow coal seam working face[J]. Journal of China Coal Society, 2019, 44(10):2945-2952.
[9] 任艳芳,宁 宇,齐庆新.浅埋深长壁工作面覆岩破断特征相似模拟[J].煤炭学报,2013,38(1):61-66.
REN Yanfang, NING Yu, QI Qingxin. Physical analogous simulation on the characteristics of overburden breakage at shallow longwall coal face[J]. Journal of China Coal Society,2013,38(1):61-66.
[10] 任艳芳,齐庆新.浅埋煤层长壁开采围岩应力场特征研究[J].煤炭学报,2011,36(10):1612-1618.
REN Yanfang, QI Qingxin. Study on characteristic of stress field in surrounding rocks of shallow coalface under long wall mining[J].Journal of China Coal Society,2011,36(10):1612-1618.
[11] 任艳芳,宁 宇,徐 刚.浅埋深工作面支架与顶板的动态相互作用研究[J].煤炭学报, 2016, 41(8): 1905-1911.
REN Yanfang, NING Yu, XU Gang. Dynamic interaction between support and roof in shallow coal seam[J].Journal of China Coal Society,2016, 41( 8):1905-1911.
[12] 朱合华,张 琦,章连洋.Hoek-Brown 强度准则研究进展与应用综述[J].岩石力学与工程学报,2013,32(10):1945-1963.
ZHU Hehua, ZHANG Qi, ZHANG Lianyang. Review of research progress and applications of Hoek-Brown strength criterion[J]. Chinese Journal of Rock Mechanics and Engineering,2013,32(10):1945-1963.
[13] Hoek E, Brown E T. Underground excavations in rocks [M]. London: Institution of Mining and Metallurgy,1980:527.
[14] Hoek E, Carranza-torres C, Corkum B. Hoek-Brown failure criterion-2002 edition[C]//Proceedings of the North American Rock Mechanics Society NARMS-TAC 2002. Toronto: University of Toronto Press, 2002:267-273.
[15] Hoek E,Brown E T. Practical estimates of rock mass strength[J]. International Journal of Rock Mechanics and Mining Sciences, 1997, 34(8): 1165-1186.
[16] Hoek E. Strength of rock and rock masses[J]. International Society for Rock Mechanics News Journal, 1994, 2(2): 4-16.
[17] Hoek E, Carranza-Torres C T, Corkum B. Hoek-Brown failure criterion-2002 edition[C]//North American Rock Mechanics Society meeting in Toronto in July 2002.
[18] Hoek E,Diederichs M S.Empirical estimation of rock mass modulus[J]. International Journal of Rock Mechanics and Mining Sciences,2006,43(2):203-215.
[19] 卢书强,许 模.基于GSI系统的岩体变形模量取值及应用[J].岩石力学与工程学报,2009,28(S1):2736-2742.
LU Shuqiang, XU Mo. Determination and application of modulus of deformation of rock masses based on gsi system[J]. Chinese Journal of Rock Mechanics and Engineering,2009,28(S1):2736-2742.
[20] 任艳芳. 浅埋深工作面覆岩“悬臂梁-铰接岩梁”结构的提出与验证[J].煤炭学报, 2019, 44(S1): 1-8.
REN Yanfang. Presentation and verification of “cantilever beam articulated rock beam” composite structure in shallow buried working face [J].Journal of China Coal Society, 2019, 44(S1): 1-8.
