0 引 言
煤炭作为我国能源基石,对国民经济和社会发展做出了巨大贡献[1]。我国煤炭以井工开采为主,煤炭开采后,井下遗留大量采空区,其在内、外荷载的扰动下可能“活化”,致使采空区地表产生残余变形,制约其开发再利用。以往,新建高速公路时常采用避让采空区的方式以保障车辆的运行安全,近年来,随着我国高速公路网的加密(截至2020年底,我国高速公路总里程已突破16×104 km),其建设将不可避免地穿越煤矿采空区,如京福高速、梅汕高速、太旧高速等。但煤矿采空区垮落带与断裂带内的破断岩体已形成采动次生平衡结构,当采空区埋深较浅时,车辆外荷载可能波及至下伏采空区,导致覆岩结构失稳、活化,诱使地表建设场地产生较剧烈的变形破坏,威胁车辆的行驶安全;而当采空区埋藏较深时,由于荷载传递的衰减效果,车辆外荷载无法波及至上述结构时,可保持采空区的稳定状态。由此可见,高速公路下伏采空区深度存在一个安全阈值,当采空区埋深大于安全阈值时新建高速公路是安全可行的;反之,则安全隐患较大。因此,如何确定高速公路下伏采空区安全深度,是进行采空区上方建设高速公路时需解决的科学问题,这与车辆荷载特性密切相关。
当前,常将车辆荷载等效为集中静荷载,再评估该集中荷载对周边附属设施稳定状态的扰动影响[2-4]。刘均利等[5]采用广义极值分布适线法拟合车辆荷载效应区间最大值样本的概率分布,对高速公路车辆荷载效应模型的建立给出了一种可行的方法,可为规范的修订研究提供参考。杨强强等[6]通过现场试验测定黄土路基下不同深度竖向土压力,研究在车辆荷载下压力的传递与扩散规律,为地下管道的设计、施工提供参考和指导。苏鹏等[7]对车辆荷载作用下的简支梁桥进行能量分析和模态参数识别研究,取得了较好的成果,给车辆荷载作用下其他桥梁结构的模态参数识别提供了新的思路。徐健等[8]通过建立综合管廊-路基土-车辆荷载有限元模型,并将数值模型计算与实测结果进行对比分析,得出在车辆荷载下管廊结构的变形规律。曹志刚等[9]通过分析车辆荷载与隧道轴线水平距离的变化对浅埋隧道动应力分布的影响和变化规律,给出不同速度下地表车辆与浅埋隧道的最小安全距离。张玥等[10]研究了车辆荷载在横向和纵向作用位置变化时,对混凝土桥面板剪力滞效应的影响,可为类似工程设计提供借鉴。
以上研究为本文研究提供了宝贵的借鉴指导,但真实的车辆荷载是一种具有动载特性的随机荷载,其在地基土体中传播产生的动力响应无法用静荷载的传播予以描述,使得上述研究成果与实际情况差异较大。因此,笔者将在考虑车辆荷载动载特性的基础上,论证、研究高速公路下伏采空区的安全深度。研究成果对于指导采空区上方高速公路建设与治理对策选取具有一定的参考价值。
1 车辆荷载特性
1.1 车辆荷载的描述
车辆行驶在不平整路上产生振动,进而引发车辆荷载。轴载100 kN的货车以不同车速行驶在IRI=2(国际平整度指数)路面上的车辆荷载如图1所示[11]。由图1可知行驶中的车辆荷载时大时小,呈波动状态。国内外研究表明,将1/4车身简化为双自由度振动模型来描述车辆的振动是合适的,如图2所示[12]。
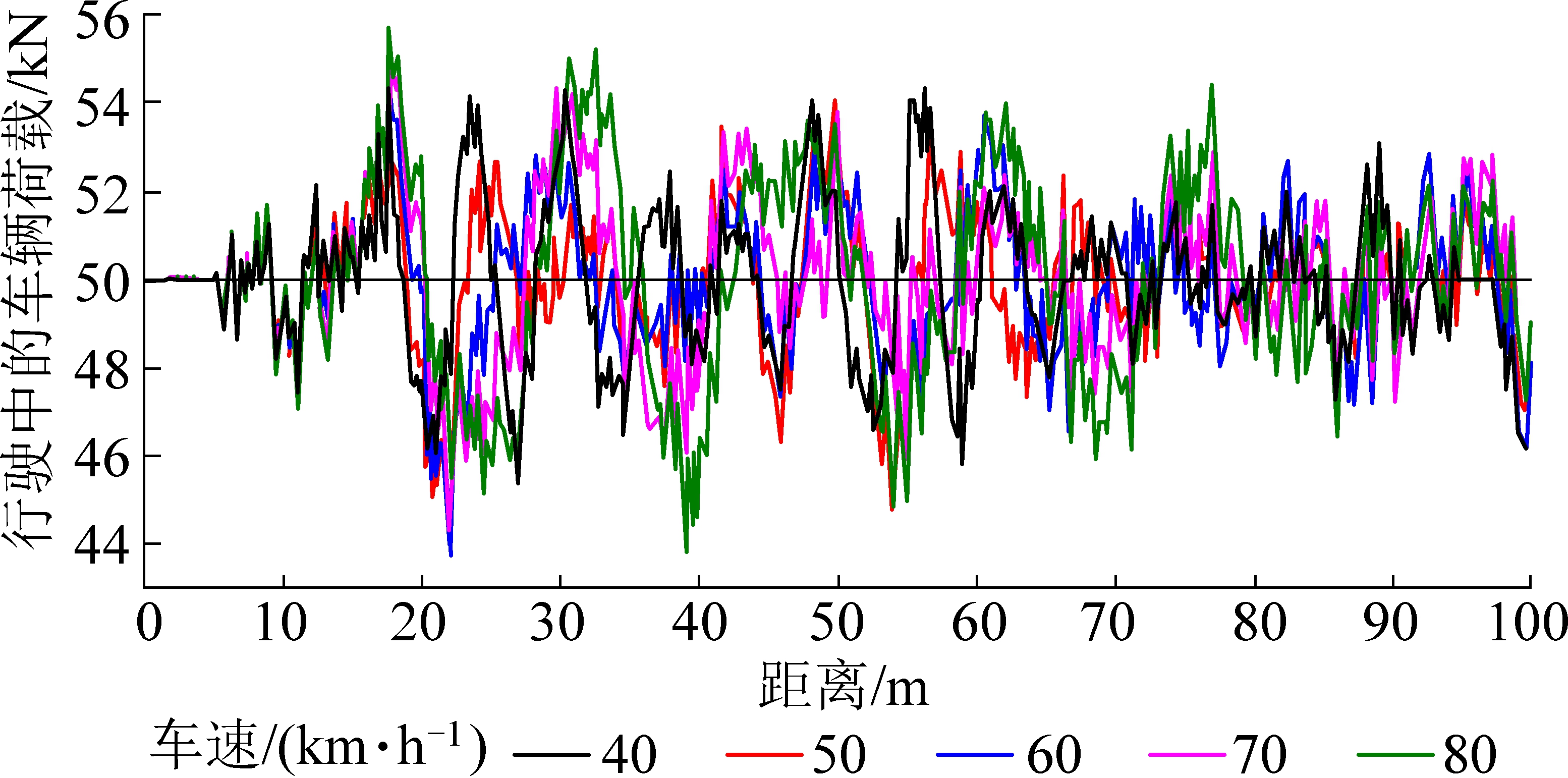
图1 车速不同时路面各点行驶中的车辆荷载[11]
Fig.1 Vehicle load of different speed [11]

m1—汽车非后悬挂部分的质量(轮胎、车轴等);m2—汽车后悬挂部分的质量(车厢、载重等);Y为悬挂部分的位移;y—非悬挂部分的位移;c1—非悬挂部分阻尼;c2—悬挂部分阻尼;a—路面不平整度,即不平顺矢高;k1—非悬挂部分的刚度;k2—悬挂部分的刚度
图2 双自由度车辆振动模型
Fig.2 Vehicle vibration model with two degrees of freedom
图2所示的振动模型微分方程可表示为
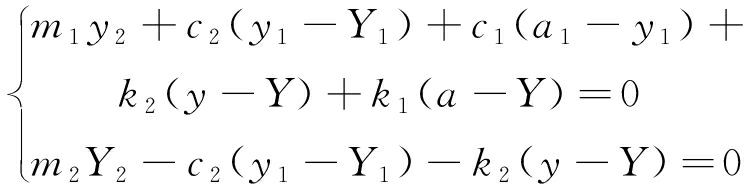
(1)
式中:Y1为悬挂部分的垂直速度;y1为非悬挂部分的垂直速度;Y2为悬挂部分的垂直加速度;y2为非悬挂部分的垂直加速度。
已有研究表明,在稳态振动时,车辆荷载与路面波形具有相同周期。假设路面不平整度为正弦函数,由式(1)可推导出车辆荷载简化表达式为
(2)
式中:P0为车辆静载;M0为簧下质量;v为车辆运行速度;L为几何曲线的波长,可取车身长;t为荷载作用时间。
虽然式(2)的表达形式简单,但其能够反映车体、道路不平整度、车辆行车速度及车辆荷载周期性等影响因素,因此,可以较准确地模拟车辆荷载。
1.2 车辆荷载的作用时间
以路面某点为例,车辆每次通过时都会对该点产生力的效果,即车辆荷载对路面某点是重复加载的。而在车辆经过的空窗期,路面某点的车辆荷载为0。凌建明等[13]给出了车辆运行速度与单次荷载作用时间的关系式,见式(3)。
t=-0.474 6ln v+2.45 2
(3)
以车辆运行速度为100 km/h为例,由式(3)计算得到单次荷载的作用时间约为0.288 s。假设高速公路上相邻车辆均能保持安全距离,由《中华人民共和国道路交通安全法》相关规定可知,车速为100 km/h时的安全车距不小于100 m,以最小安全车距100 m为例,时速100 km/h的车需要3.888 s才可通过,也就是说,车辆荷载的空窗期为3.888 s,其作用时间示意如图3所示。
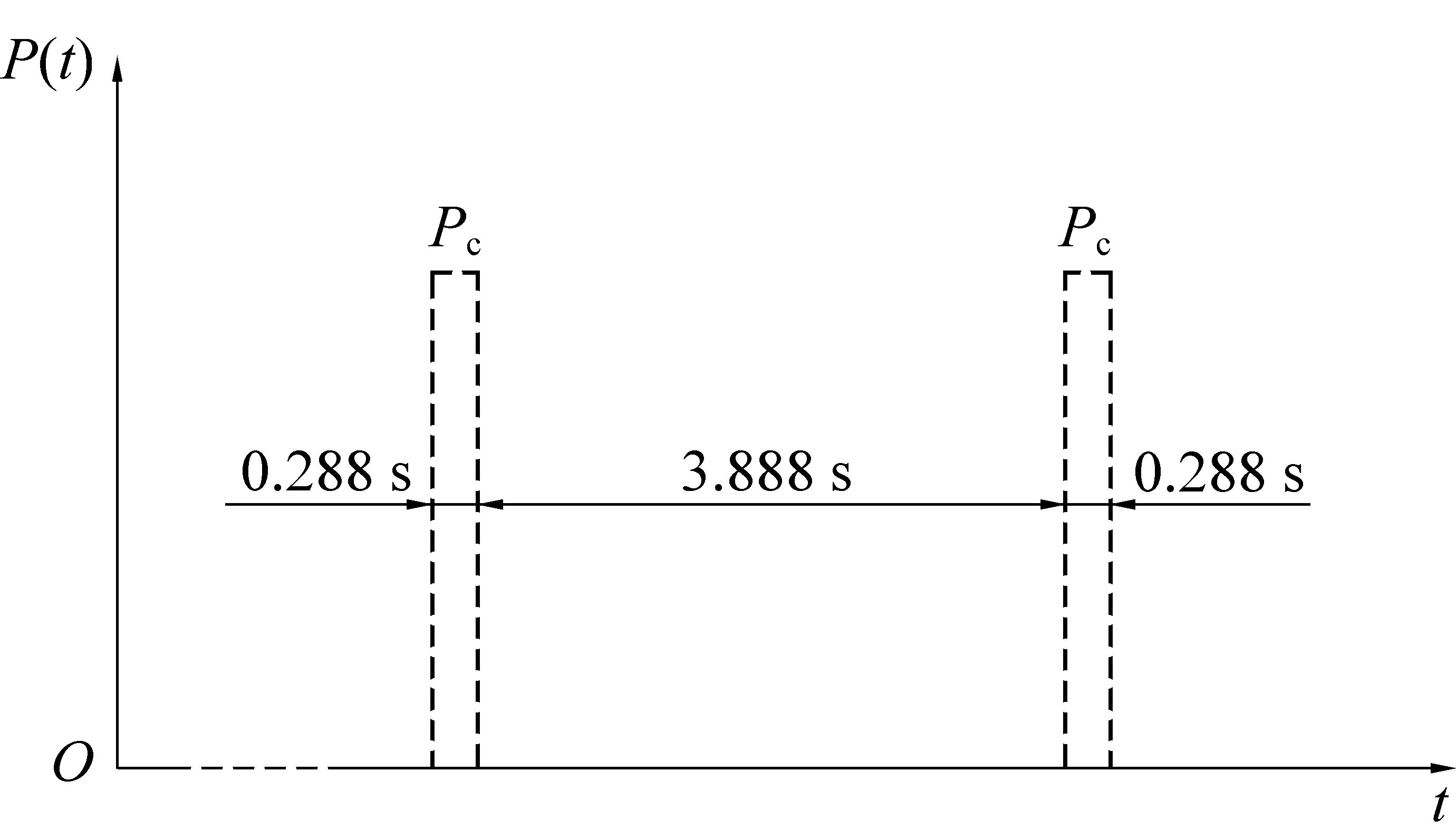
图3 路面某点车辆荷载作用时间示意(100 km/h)
Fig.3 Sketch of vehicle load time at a point on road (100 km/h)
2 车辆荷载扰动深度的数值模拟
采用UDEC模拟研究车辆荷载的扰动深度,该计算分析程序由Cundall提出,可较好地模拟研究动、静荷载作用下连续或非连续介质的力学响应。
1)边界条件。为避免动力波在模型中反射振动无法消散,影响分析结果,采用可以吸收入射波的黏性边界作为此次动力模型的边界条件。
2)阻尼类型。考虑到瑞利阻尼的理论与常规动力分析方法类似,得到的加速度响应规律与实际比较吻合,采用瑞利阻尼,其中心频率的参数Freq可采用系统的自振频率,阻尼比的参数Fcrit一般按经验选取为2%~5%。
3)本构模型。随着车辆荷载的循环次数增加,路基土体逐渐硬化,应变增速逐渐减小,变形模量逐渐增大。也就是说,采用硬化弹塑性模型(HS)能够准确分析车辆荷载作用下的路基变形特征,但其参数难于获取,而文中主要研究车辆荷载的扰动深度,并非路基的变形特性。为方便计算,采用摩尔库伦理想弹塑性屈服准则描述路基及下方岩土体的本构关系,线弹性本构模型描述路面的本构关系。在模拟试验过程中,路基土体的内摩擦角、黏聚力等参数保持不变,由此得到的模拟结果相比硬化模型的略大,是偏安全的,能够满足工程需求。
4)模拟过程。模拟主要分4步进行:①建立初始模型,使其在重力条件下迭代平衡;②开采煤层,形成采空区;③对采空区内破断岩体进行参数折减(一般为原始参数的1/3~1/5[14-15]);④在模型顶端输入车辆荷载,进行迭代计算。
5)扰动深度的判定条件。一般情况下,常采用应力和应变2种标准来判定荷载的扰动深度[16-18]:①对应力标准而言,当土体附加应力为土体自重力的10%时,此深度可视为外荷载的扰动深度;②对应变标准而言,当土体应变ε<0.001%时,可忽略土体的塑性累积变形,此时的深度可视为外荷载的扰动深度。综合比选上述2种标准的适用性,选取应力标准作为荷载扰动深度的判定标准。
3 不同工况条件下车辆荷载的扰动深度
通过建立25组数值模拟试验来表征25种不同工况条件,模拟研究不同路堤高度、路面刚度、车辆载重及行车速度的车辆荷载扰动深度。
3.1 不同路堤高度的荷载扰动深度
此组共设计6种工况数值模拟试验(工况1-6号),分别模拟研究路堤高度为0、2、4、6、8和10 m的车辆荷载扰动深度,试验方案所需力学参数见表1。模拟在这6种工况条件下,路面刚度为1 200 MPa,路堤填料及填筑指标不随路堤高度变化而改变,即路堤材料属性恒定,车辆荷载模型以小轿车为例,车辆荷载的具体参数见表2。模拟结果如图4所示。
表1 路堤高度影响的试验方案力学参数
Table 1 Mechanical parameters of test scheme for embankment height influence
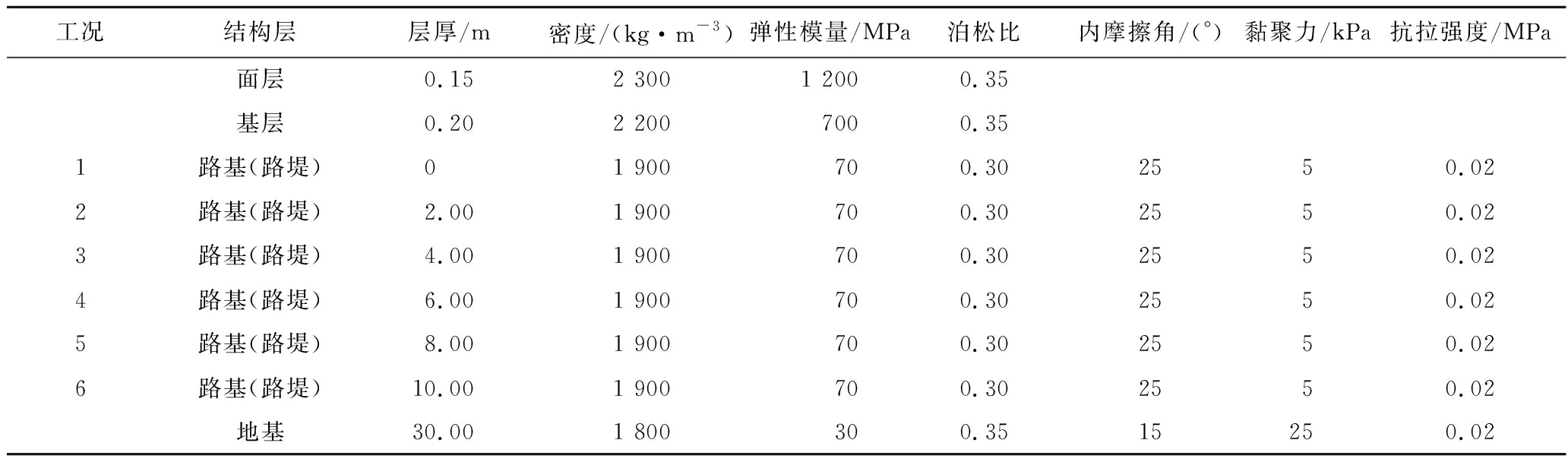
工况结构层层厚/m密度/(kg·m-3)弹性模量/MPa泊松比内摩擦角/(°)黏聚力/kPa抗拉强度/MPa面层0.152 3001 2000.35基层0.202 2007000.351路基(路堤)01 900700.302550.022路基(路堤)2.001 900700.302550.023路基(路堤)4.001 900700.302550.024路基(路堤)6.001 900700.302550.025路基(路堤)8.001 900700.302550.026路基(路堤)10.001 900700.302550.02地基30.001 800300.3515250.02
表2 小轿车荷载参数
Table 2 Load parameters of car

车辆类型车身长度/m簧下质量/kg车辆静轮载/kN车辆运行速度/(km·h-1)几何不平顺矢高/mm小轿车6120201002
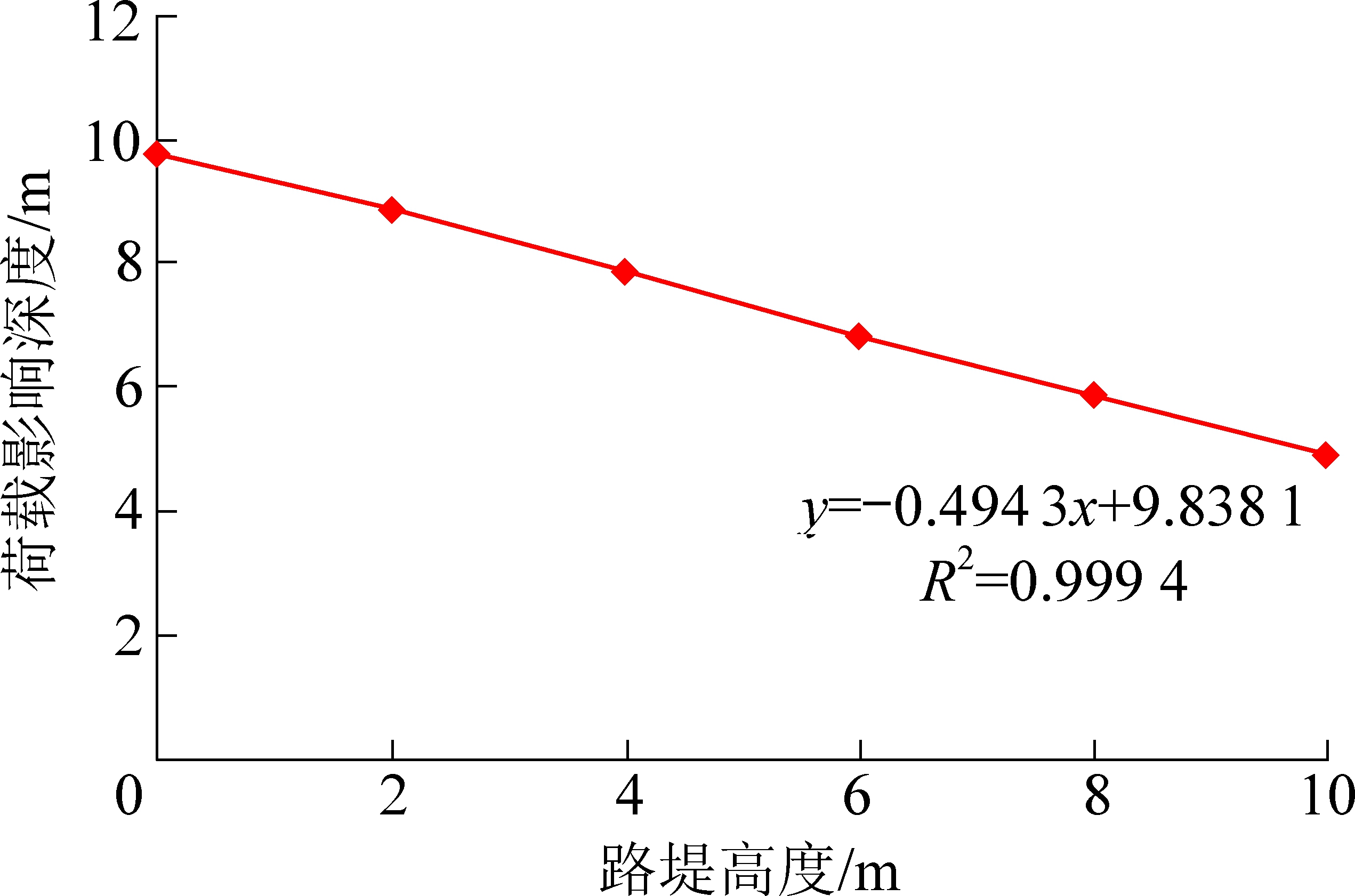
图4 车辆荷载影响深度与路堤高度关系
Fig.4 Relationship between vehicle load disturbance depth and embankment height
由图4可知,路堤高度与车辆荷载影响深度间呈线性相关,随着路堤高度的增加,荷载扰动深度逐渐减小,即车辆经过低路堤路段时的扰动深度更大。因此,在采空区上方修建高速公路时,应尽量避免设计低路堤路段。
3.2 不同路面刚度的荷载扰动深度
根据路面材料的不同可分为刚性路面、半刚性路面和柔性路面。通过更改路面材料弹性模量的方式,研究路面刚度对扰动深度的影响,也设计6组数值模拟试验(工况7-12号),模拟研究路面刚度分别为800、1 600、2 400、3 200、4 000和4 800 MPa,而路堤高度均为2 m,车辆载重均为2 t,车辆速度均为100 km/h的车辆荷载扰动深度。试验所需力学参数见表3。模拟结果如图5所示。
表3 路面刚度影响的试验方案力学参数
Table 3 Mechnaical parameters of test scheme for pavement stiffness influence
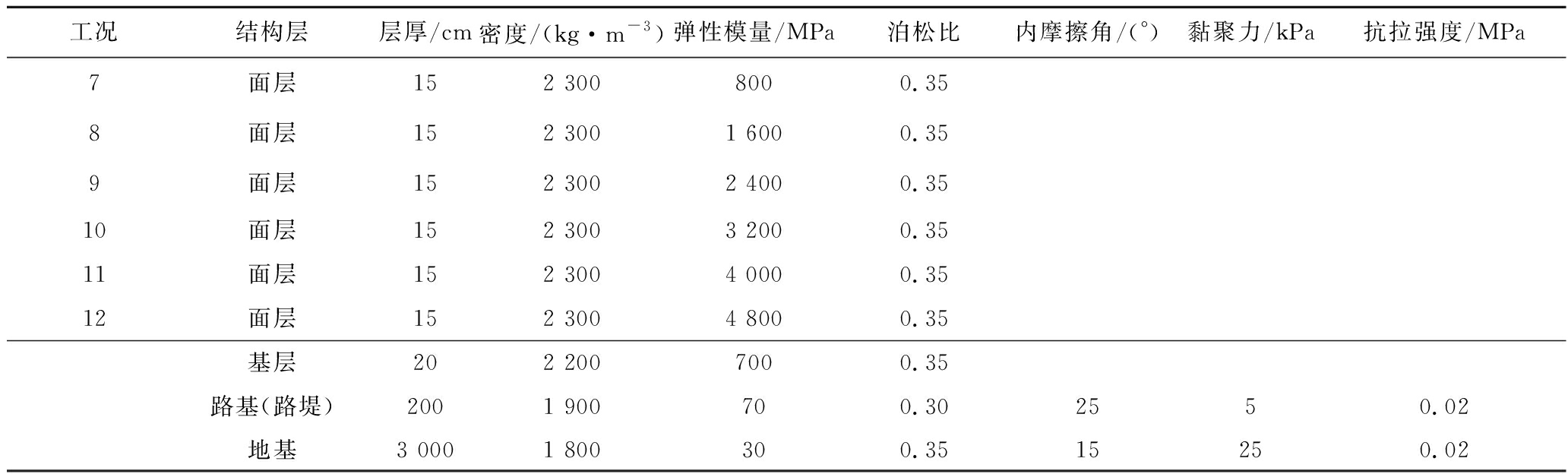
工况结构层层厚/cm密度/(kg·m-3)弹性模量/MPa泊松比内摩擦角/(°)黏聚力/kPa抗拉强度/MPa7面层152 3008000.358面层152 3001 6000.359面层152 3002 4000.3510面层152 3003 2000.3511面层152 3004 0000.3512面层152 3004 8000.35基层202 2007000.35路基(路堤)2001 900700.302550.02地基3 0001 800300.3515250.02
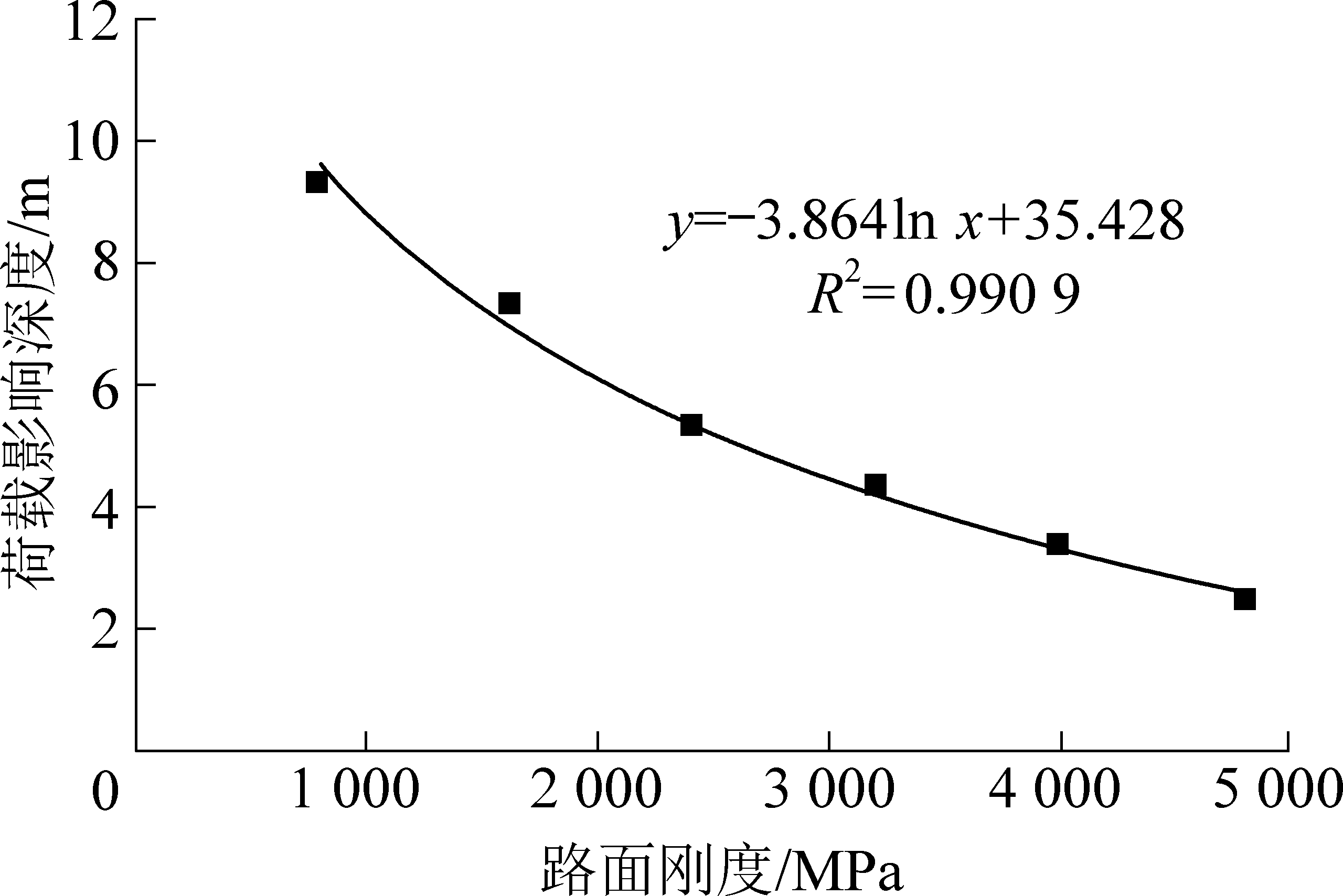
图5 车辆荷载影响深度与路面刚度关系
Fig.5 Relationship between vehicle load disturbance depth and pavement stiffness
由图5可知,随着路面刚度的增大,荷载扰动深度逐渐减小。在路面刚度较小时,随着刚度的增加,荷载扰动深度下降较快,而当路面刚度超过2 400 MPa时,随着刚度的增加,荷载的扰动深度下降较慢。路面刚度与车辆荷载扰动深度之间非线性相关,可采用对数函数拟合二者之间的关系(图5)。
3.3 不同车辆载重的荷载扰动深度
以特大车为例(表4),同理,再设计6组数值模拟试验(工况13-18号),分别模拟研究特大车载重为5、10、20、30、40和50 t时的荷载扰动深度。该6种工况中的路面刚度为1 200 MPa,路堤高度为2 m,车辆运行速度为100 km/h,模型中的其他力学参数见表1。模拟结果如图6所示。
表4 特大车载荷参数
Table 4 Load parameters of oversized vehicle

车辆类型车身长/m簧下质量/kg车辆静轮载/kN车辆运行速度/(km·h-1)几何不平顺矢高/mm特大车121 1801201002
由图6可知,当车辆载重较小时,随着载重的增加,车辆荷载的扰动深度急剧增加,而后随着载重的增加,荷载的扰动深度增加缓慢,当载重达到50 t时,车辆荷载的影响深度为29.7 m。车辆载重与车辆荷载扰动深度之间非线性相关,可采用对数函数拟合二者之间的关系。
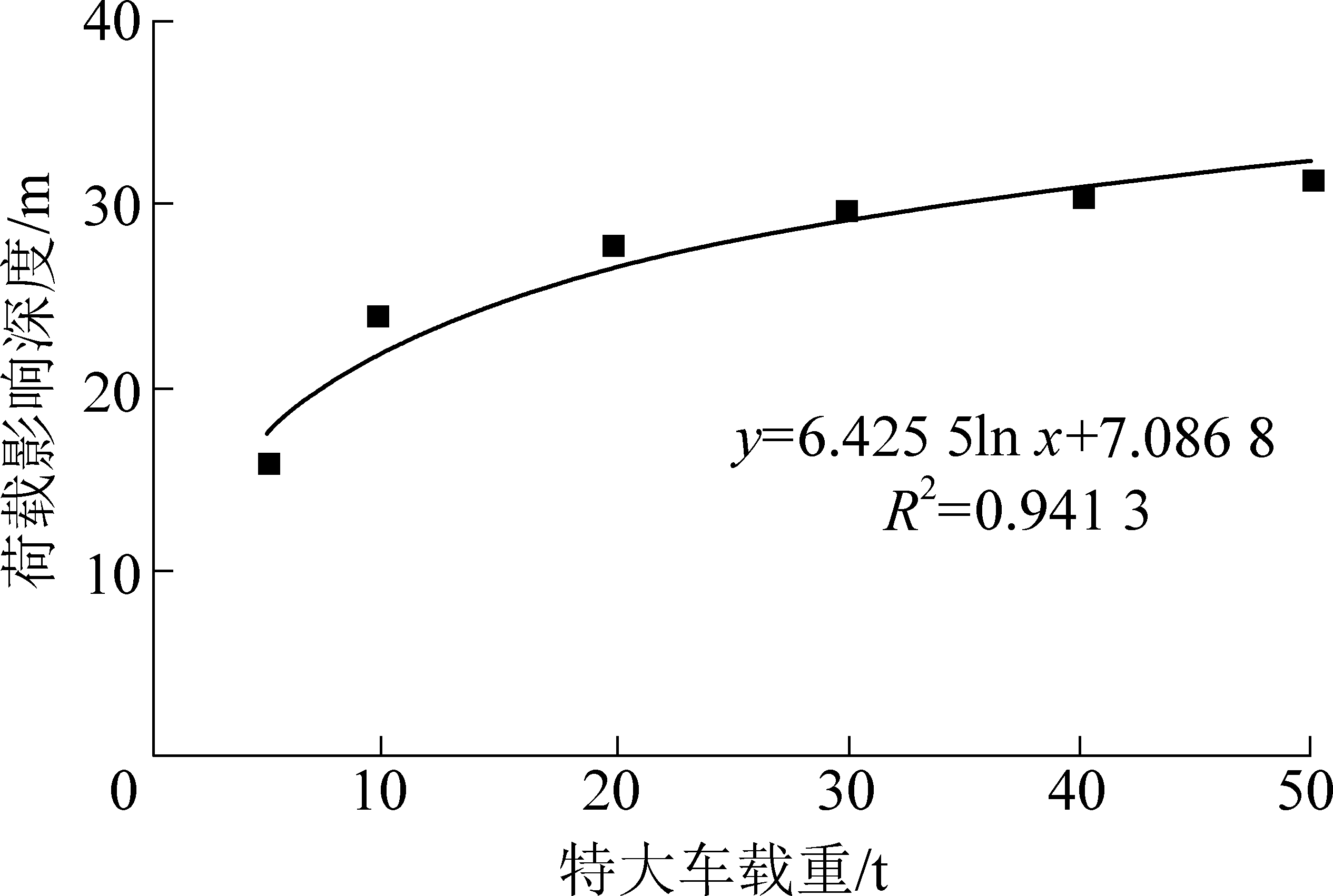
图6 车辆荷载影响深度与车辆载重关系
Fig.6 Relationship between vehicle load disturbance depth and vehicle load
3.4 不同行车速度的荷载扰动深度
以小轿车为例(表2),共设计7组数值模拟试验(工况19—25号),模拟研究车辆运行速度分别为60、70、80、90、100、110和120 km/h时的荷载扰动深度。在这7种工况中的路面刚度均为1 200 MPa,路堤高度为2 m,车辆载重2 t,模型中的其他力学参数参见表1。模拟结果如图7所示。
由图7可知,随着车辆速度的增大,荷载的影响深度逐渐减小,这是由于当车辆运行速度较慢时,车辆荷载对地基的作用时间相对较长导致的。车辆运行速度为60 km/h时,荷载的扰动深度为18.8 m,当车辆运行速度增加到120 km/h时,荷载的扰动深度减小到7.5 m。车辆运行速度与荷载扰动深度之间非线性相关,可采用对数函数拟合二者之间的关系,拟合结果如图7所示。
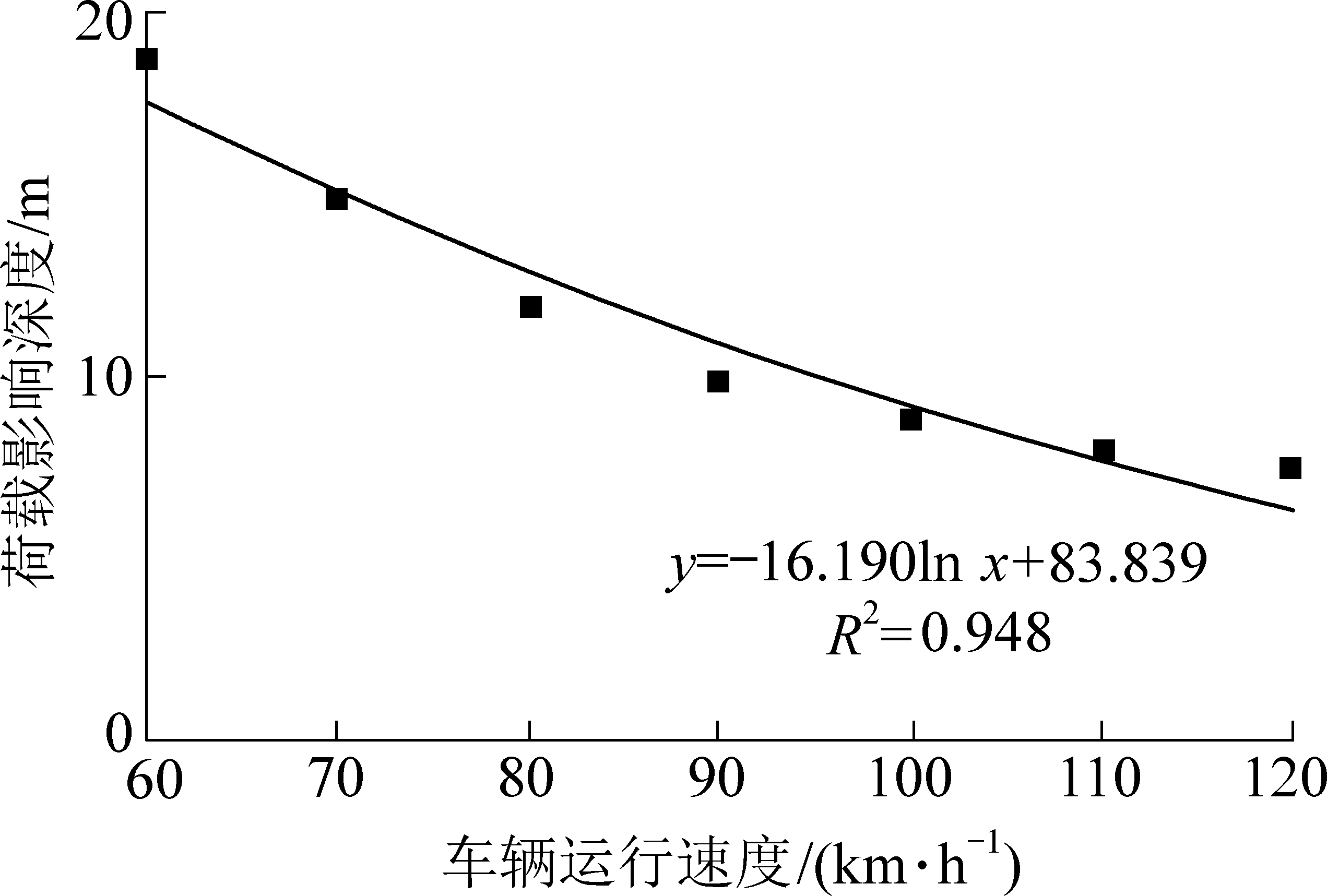
图7 车辆荷载影响深度与车辆速度关系
Fig.7 Relationship between vehicle load disturbance depth and vehicle velocity
此外,还对道路不平整度对车辆荷载扰动深度的影响进行了研究,结果表明道路不平整度对其影响较小,基本可以忽略该因素的影响。
4 高速公路下伏采空区安全深度的确定
4.1 车辆荷载扰动深度经验公式
由前文分析可知,车辆荷载扰动深度与路堤高度、路面刚度、车辆载重及行车速度密切相关,而上述4个因素相互独立,基于叠加原理,可以得到车辆荷载扰动深度的经验公式,如式(4)所示。
hd=a1hl+a2ln Em+a3ln L0+a4ln v+a0
(4)
式中,hl为路堤高度;Em为路面刚度;L0为车辆载重;a1、a2、a3、a4和a0为系数。
基于具体的数值模拟试验结果,采用多元回归分析理论[19]对式(4)中的系数ai进行拟合,拟合度和拟合结果见表5~表6。由表5可知,相关系数为0.994,表明本文选取的4个影响因素与车辆荷载的扰动深度之间相关程度较大,调整后的复测定系数为0.986,说明本文选取的4个因素可靠有效,能够揭示车辆荷载扰动深度的变化关系。由表6中的标准化回归系数可知,对车辆荷载扰动深度影响最大的是车辆载重,其次是车辆运行速度,随后是路面刚度,最后是路堤高度。
表5 回归统计
Table 5 Regression statistics

参量相关系数判定系数复测定系数标准误差观测值数值0.9940.9880.9861.06925
表6 回归参数
Table 6 Regression parameters
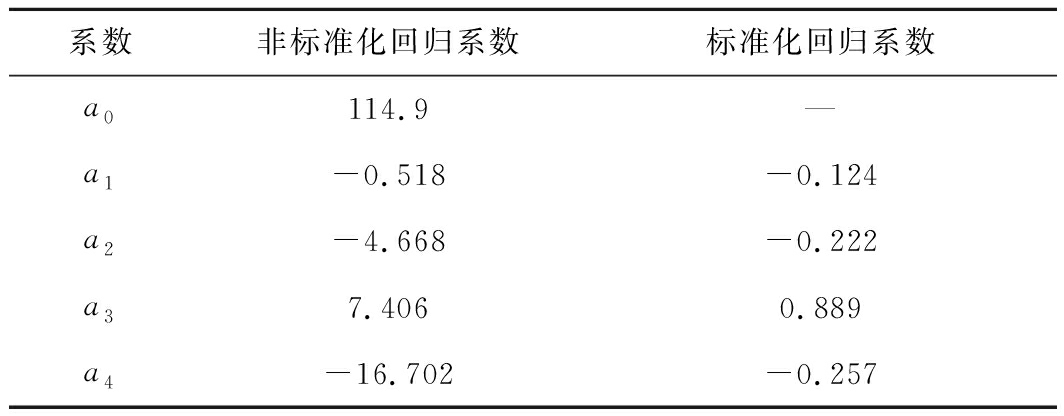
系数非标准化回归系数标准化回归系数a0114.9—a1-0.518-0.124a2-4.668-0.222a37.4060.889a4-16.702-0.257
将表6中的非标准化回归系数代入式(4)即可得到车辆荷载扰动深度经验公式,即式(5)。
将前文第3节中25种工况条件下的经验公式计算值与数值模拟实验值的比较结果如图8所示,假设上述数值模拟实验值为真值。
由图8可知,经验公式计算值的残差介于0~2.8 m,除最后一种工况(相对误差为20%)外,其余工况的经验公式计算结果相对误差均小于10%,进一步计算得出经验公式计算值的均方根误差约为0.95 m,由此可知,该经验公式计算结果与数值模拟实验值偏差较小,能够满足工程需求。
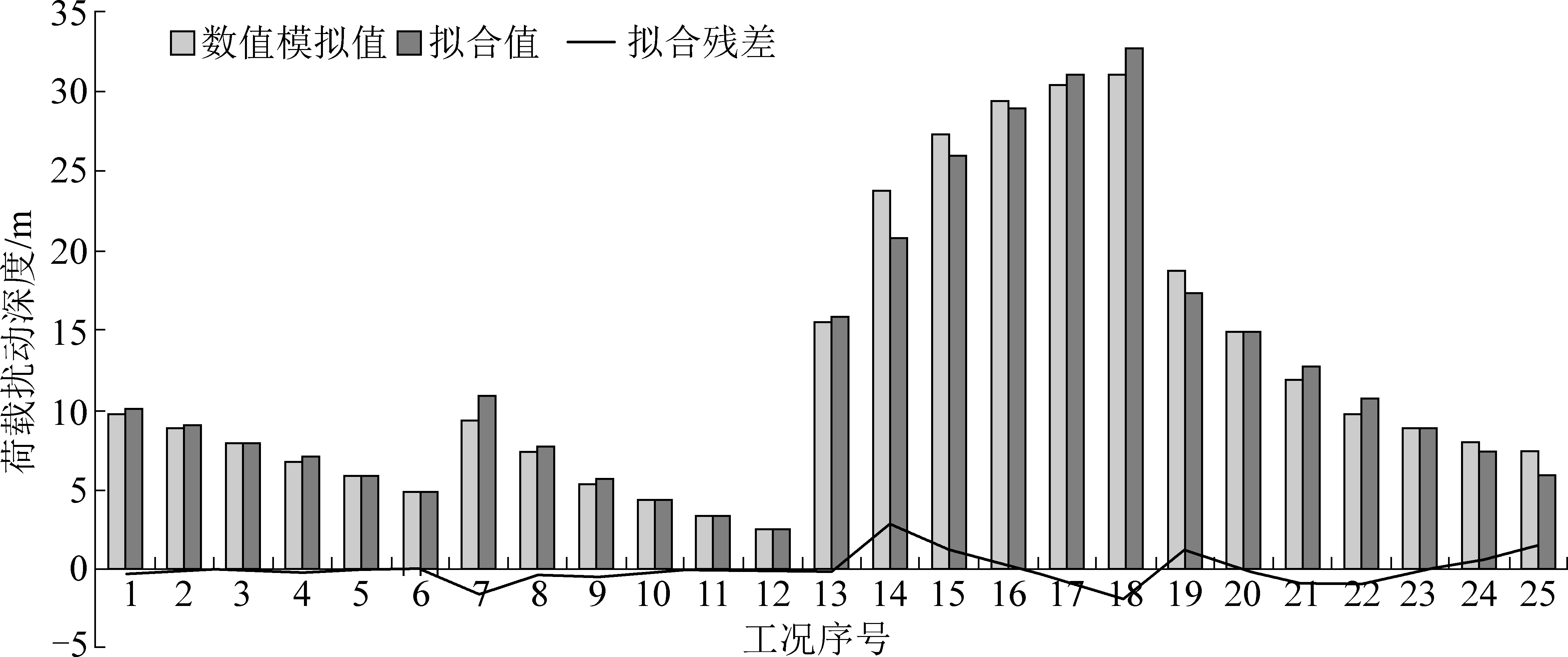
图8 经验公式计算效果
Fig.8 Calculation ability of the empirical formula
hd=-0.518hl-4.668ln Em+
7.406ln L0-16.702ln v+114.9
(5)
4.2 采空区安全深度的计算
采空区内的垮落带和断裂带岩体处于相对稳定状态,受车辆荷载的扰动,垮落带的破断岩体和断裂带的砌体梁结构可能发生变形失稳,诱使其“活化”,进而威胁其上方高速公路车辆的行驶安全。为保障废弃采空区岩体结构的平衡状态,避免其受到车辆外荷载的扰动影响,则废弃采空区的安全深度应大于车辆荷载扰动深度与导水裂隙带高度之和,即
Hs>hd+Hli
(6)
式中:Hs为安全深度;Hli为导水裂隙带高度。
4.3 工程应用
武云高速位于焦作市的修武、武陟县境内,是河南省高速公路“十一五”规划的重点工程,采用四车道高速公路标准进行设计,设计时速为100 km/h,路线全长约36.832 km,其中K30+800~K32+900路段穿越采空区。以武云高速下伏采空区为原型,铺设了相似材料模型,模型的几何相似比Cl=1∶300;时间相似比Ct=1∶17.3;容重相似比Cr=1.6;应力相似比CR=1∶480。相似模拟试验中各岩层的相似材料配比,见表7。
表7 相似材料配比
Table 7 Ratios of similar material

岩层材料占比/%(质量比)河沙∶云母∶胶结料胶结料占比/%(质量比)石膏碳酸钙冲积层94∶4∶20.61.4砂质泥岩93∶4∶31.51.5粉砂岩93∶4∶32.10.9砂泥互层93∶4∶31.51.5细砂岩92∶4∶42.81.2砂质泥岩93∶4∶31.51.5泥岩392∶5∶31.21.8中砂岩93∶4∶31.51.5泥岩191∶6∶30.92.0煤层93∶4∶32.00.9底板岩层89∶3∶85.62.4
除冲积层外,各岩层材料在搅拌过程中加水总量均为材料总质量的10%,冲积层加水总量为材料总质量的15%。为增加冲积层的松散性,并方便煤层后期开挖,实验过程中对冲积层和煤层材料额外增加了锯末,其中冲积层增加锯末总量为该岩层材料总质量的10%,煤层增加锯末总量为该岩层材料总质量的5%。
模拟结果如图9所示,武云高速下伏采空区内导水裂隙带的发育形态为非对称的马鞍形,采空区上山方向导水裂隙带发育较高,约为60 m,下山方向约为47.5 m。

图9 武云高速下伏废弃采空区覆岩破坏情况
Fig.9 Characteristics of overlying strata failure in abandoned goaf under Wuyun Expressway
假设武云高速路堤高度为0,路面刚度为800 MPa,车辆载重为50 t,运行速度为60 km/h,将上述参数代入式(5),可得车辆动荷载扰动深度最大值约为44 m。
结合式(6)可计算,武云高速下伏采空区的安全深度应超过104 m。由现场调研资料可知,武云高速下伏采空区最浅处为158 m,大于安全深度,因此,车辆荷载不会波及至下伏采空区,导致其结构失稳、活化。
5 结 论
1)给出了车辆荷载扰动深度数值模拟研究的方法,包括边界条件设置、阻尼类型选择、本构模型选取、模拟过程及判定条件等,其模拟过程可分为4步:①建立初始模型;②形成采空区;③破断岩体参数折减;④施加车辆荷载。
2)车辆荷载扰动深度随路堤高度、路面刚度及行车速度的增加而减小,随车辆载重的增加而增大;扰动深度与路堤高度呈线性相关,与路面刚度、车辆载重及行车速度呈非线性相关。基于叠加原理得出了车辆荷载扰动深度的经验公式,基于多元回归分析拟合出经验公式中的系数。
3)给出了高速公路下伏采空区安全深度的计算方法:安全深度应大于车辆荷载扰动深度与导水裂隙带发育高度之和。将研究成果应用于武云高速,结果表明武云高速下伏采空区安全深度应超过104 m,小于武云高速下伏采空区最浅埋深158 m,即武云高速车辆荷载不会波及至下伏采空区,导致其结构失稳、活化。
[1] 王国法,刘 峰,孟祥军,等. 煤矿智能化(初级阶段)研究与实践[J]. 煤炭科学技术,2019,47(8):1-36.
WANG Guofa,LIU Feng,MENG Xiangjun,et al. Research and practice on intelligent coal mine construction(primary stage) [J]. Coal Science and Technology,2019,47(8):1-36.
[2] 丁森林,钱德玲,戴启权,等. 车辆荷载影响下深基坑开挖稳定性分析[J]. 合肥工业大学学报(自然科学版),2019,42(5):671-676.
DING Senlin,QIAN Deling,DAI Qiquan,et al. Analysis on the stability of deep foundation pit excavation under vehicle loads [J]. Journal of Hefei University of Technology(Natural Science),2019,42(5):671-676.
[3] 邓鹏宏,王海龙. 车辆荷载作用下露天矿采空区顶板安全厚度研究 [J]. 金属矿山,2016(3):62-66.
DENG Penghong,WANG Hailong. Study on safety thickness of goaf roof under the vehicle load in open-pit iron mine [J]. Metal Mine,2016(3):62-66.
[4] 白旭峰,张 晶,苏晓果. 车辆荷载作用下软土地基上预制综合管廊受力特征分析[J]. 黑龙江大学工程学报,2018,9(4):19-22.
BAI Xufeng,ZHANG Jing,SU Xiaoguo. Analysis of mechanical characteristics of precast concrete utility tunnel on soft soil foundation induced by vehicle loads [J]. Journal of Engineering of Heilongjiang University,2018,9(4):19-22.
[5] 刘均利,余学志,余文成,等. 采用广义极值分布的公路桥梁车辆荷载效应极值预测[J]. 华侨大学学报(自然科学版),2019,40(4):470-475.
LIU Junli,YU Xuezhi,YU Wencheng,et al. The extreme value prediction of load effect of road and bridge vehicles with broad extreme value distribution is predicted [J]. Journal of Huaqiao University (Natural Science),2019,40 (4): 470-475.
[6] 杨强强,丁小军,王 旭,等. 车辆荷载作用下黄土路基竖向土压力传递规律研究[J]. 公路交通科技,2021,38(2):40-47.
YANG Qiangqiang,DING Xiaojun,WANG Xu,et al. Study on vertical earth pressure transfer law of loess subgrade under vehicle load [J]. Journal of Highway and Transportation Research and Development,2021,38(02):40-47.
[7] 苏 鹏,陈彦江,闫维明. 车辆荷载作用下简支梁桥动力特性分析及模态参数识别[J]. 工业建筑,2019,49(5):62-66,153.
SU Peng,CHEN Yanjiang,YAN Weiming. Dynamic characteristics analysis and modal parameter identification of simply supported beam bridge under vehicle load [J]. Industrial Construction,2019,49(5):62-66,153.
[8] 徐 健,谢忠球,吴敬龙. 车辆荷载作用下综合管廊变形特性研究[J]. 建筑结构,2019,49(S1):845-849.
XU Jian,XIE Zhongqiu,WU Jinglong. Research on deformation characteristics of comprehensive pipe gallery under vehicle load [J]. Building Structure,2019,49(S1):845-849.
[9] 曹志刚,唐 浩,袁宗浩,等. 地表交通荷载引起邻近浅埋隧道振动评价研究[J]. 岩石力学与工程学报,2019,38(8):1696-1706.
CAO Zhigang,TANG Hao,YUAN Zonghao,et al. Surface traffic load caused by nearby shallow buried tunnel vibration evaluation study [J]. Chinese Journal of Rock Mechanics and Engineering,2019,38 (08): 1696-1706.
[10] 张 玥,郭劲岑. 车辆荷载作用下钢板组合连续梁桥桥面板应力分析[J]. 应用力学学报,2019,36(3):741-746,768.
ZHANG Yue,GUO Jinxuan. Stress analysis of steel plate combination continuous beam bridge panel under vehicle load [J]. Chinese Journal of Applied Mechanics,2019,36(3):741-746,768.
[11] 江雨岑. 行驶中的车辆荷载波动及其对沥青路面结构设计的影响[D]. 哈尔滨: 哈尔滨工业大学,2015.
[12] 张子月,王云广,张志杰,等. 高速公路动荷载对塌陷区的扰动分析[J]. 中国安全生产科学技术,2015,11(1):106-111.
ZHANG Ziyue,WANG Yuaguang,ZHANG Zhijie,et al. Analysis on disturbance to subsidence area by dynamic load of highway [J]. Journal of Safety Science and Technology,2015,11(1):106-111.
[13] 凌建明,王 伟,邬洪波. 行车荷载作用下湿软路基残余变形的研究[J]. 同济大学学报(自然科学版),2002,30(11):1315-1320.
LING Jianming,WANG Wei,WU Hongbo. Research on residual deformation of saturated clay subgrade under vehicle load [J]. Journal of Tongji University(Natural Science),2002,30(11):1315-1320.
[14] 童立元,邱钰,刘松玉,等. 高速公路与下伏煤矿采空区相互作用规律探讨[J]. 岩石力学与工程学报,2010,29(11):2271-2276.
TONG Liyuan,QIU Yu,LIU Songyu,et al. Discussion of interaction law of expressway and underlying mine goafs [J]. Chinese Journal of Rock Mechanics and Engineering,2010,29(11):2271-2276.
[15] 杨撷民,霍俊杰,李彦荣. 基于MIDAS软件对受采空区影响坡体的稳定性研究[J]. 煤炭科学技术,2019,47(8):89-95.
YANG Xiemin,HUO Junjie,LI Yanrong. Study on stability of slope affected by goaf based on MIDAS software [J]. Coal Science and Technology,2019,47(8): 89-95.
[16] 孙吉书,梅林健,杨 辉. 施工车辆荷载对低路堤软土地基的影响深度分析[J]. 河北工业大学学报,2018,47(4):93-97.
SUN Jishu,MEI Linjian,YANG Hui. Analysis on the influential depth of construction vehicle load in low embankment soft subsoil[J]. Journal of Hebei University of Technology,2018,47(4):93-97.
[17] 任连伟,周桂林,顿志林,等. 采空区建筑地基适宜性及沉降变形计算工程实例分析[J]. 岩土力学,2018,39(8): 2922-2932.
REN Lianwei,ZHOU Guilin,DUN Zhilin,et al. Case study on suitability and settlement of foundation in goaf site[J]. Rock and Soil Mechanics,2018,39(8): 2922-2932.
[18] MAIR R J. Developments in geotechnical engineering research:application to tunnels and deep excavations[J]. Journal of Periodontology,1992,93(1):759-62.
[19] 卢晨刚,张遂安,白铁峰,等. 川南筠连区块煤层三维含气量属性精细建模 [J]. 煤炭科学技术,2019,47(8):219-225.
LU Chengang,ZHANG Suian,BAI Tiefeng,et al. Improved modeling of 3D gas content attributes of CBM in Junlian Region of southern Sichuan [J]. Coal Science and Technology,2019,47(8):219-225.
