0 引 言
地下岩体中充满着裂隙,它对油气资源开发、地下水资源利用、污染物迁移、二氧化碳封存以及核废物地质处置等具有重要意义[1-3],因此,正确评价裂隙岩体的连通性和渗流特征显得尤为重要[4-6]。然而,由于地质作用的多样性,岩体被不同尺度和方向的裂隙切割,形成空间变异性和各向异性强的裂隙介质,构成了复杂的裂隙网络系统[7]。在岩石露头调查中,少数大型裂隙的几何特征较易确定,但大量的裂隙埋藏在岩体内部,很难逐个测量,这对获得全面的露头裂缝信息是一个挑战[8]。然而,利用野外统计与摄影技术相结合建立数字模型,可以准确地获得相应的参数[9]。
一般来说,通过盘状裂隙网络渗流模型分析裂隙连通性和渗流特性的方法有3种:有限元法;离散元法;将DFN转换为与平面裂缝具有近似等效连接性和水力特性的网络管道,也称为“管网模型”[10]。对于管网模型,TSANG[11]指出,渗流裂缝随势梯度方向而变化,通常沿阻力最小的主渗流方向流动。CACAS等[12]在断裂面上使用圆形流动管并提出了管道模型。基于此,NORDQVIST等[13]建立了裂隙岩体中流动和运移的三维裂隙网络模型。随后,CLEMO等[14]进一步发展了CACAS管道模型。一般来说,裂隙岩体中流体的流动是沿优先路径,基于CHAN3D程序,GYLING[15]建立了用于模拟流体流动和溶质运移的通道网络模型,利用简单的稳态水力和几何数据研究了流道的水力特性和水力结构。由于裂隙岩体的非均质性,裂隙长度影响裂隙孔径的大小,BRUDERER-WENG等[16]在非均质和使用管网中的量化流渠化研究其与分散的关系,分别通过改变管径分布的标准化标准偏差和对其空间分布施加指数变异函数,探讨了孔径不均匀性和相关长度的影响,得到了体积流量和压力梯度场的完整描述。XU等[17]结合裂缝网络连通性分析和流动建模的迭代方法,以导出等效管网模型提出了一个等效管网模型,并与现有方法的结果进行了比较,证明了该方法产生真实流动模式的潜力。BAGALKOT[18]采用可变孔径模型,而不是传统的平行板模型,研究了单个耦合裂隙基质系统中放射性核素的输运,指出了传统平行板模型的不足。WANG[19]将PNM与离散单元法(DEM)相结合,模拟裂隙岩体中的渗流,提出了粒子力学方法模拟节理岩体力学行为的建模技术。DESSIRIER等[20]开发了库Pychan3d,以模拟深部地下有通道网络的裂隙岩石中的流动和运输,得出了适用于非结构化渠道网络建模方法。但是目前的研究中采用的管网模型主要为同截面,模型与实际相比简化较大,导致结果可能误差较大。
笔者使用变截面等效管来模拟岩体裂缝的渗透特性,而不是每个通道宽度不同的矩形截面,将复杂的裂隙盘网络等效为管网模型,研究岩体的连通性和水力特性。在离散裂隙模型中,笔者将一定厚度的裂隙盘等效为变直径三维管网模型,并在此基础上提出等效路径渗透系数,反映了实际路径下的渗透特性,更加客观地研究了裂隙岩体的渗透特性。
1 研究背景及等效管网模型的渗流分析
研究地点是甘肃省北山地区的新昌遗址,这是中国HLW知识库建设的第一个地点。本区地质构造以花岗岩为主。由于花岗岩本身的特点和其他地质作用的影响,有裂缝的花岗岩在露头上暴露良好。这些完全裸露的典型露头对研究具有重要意义,同时,该地区也是一个很好的自然试验场。
根据二维图论,管网方法同样适用于三维情况。圆形裂缝的中心和2个圆形裂隙相交形成的横截面被定义为内部节点。圆形裂隙与边界边相交的中心生成外部节点。节点间的渗流通道由等效渗流管模拟,主要有3种建模方法(图1)[21]。

eavg—平均水力宽度;w—界面厚度;rh—水力半径
图1 不同裂隙宽度的渗流建模方法
Fig.1 Seepage modeling method with different fracture width
使用变截面等效管来模拟岩体裂缝的渗透特性,而不是每个通道宽度不同的矩形截面。基于等面积原理,由2个圆形裂缝相交形成的矩形截面相当于圆形截面,圆形裂缝中心的矩形截面也相当于圆形截面(图2),其中:emax为最大水力; r为等效管半径;对于方形等效管,L为其边宽,对于圆形等效管,L等于其直径。
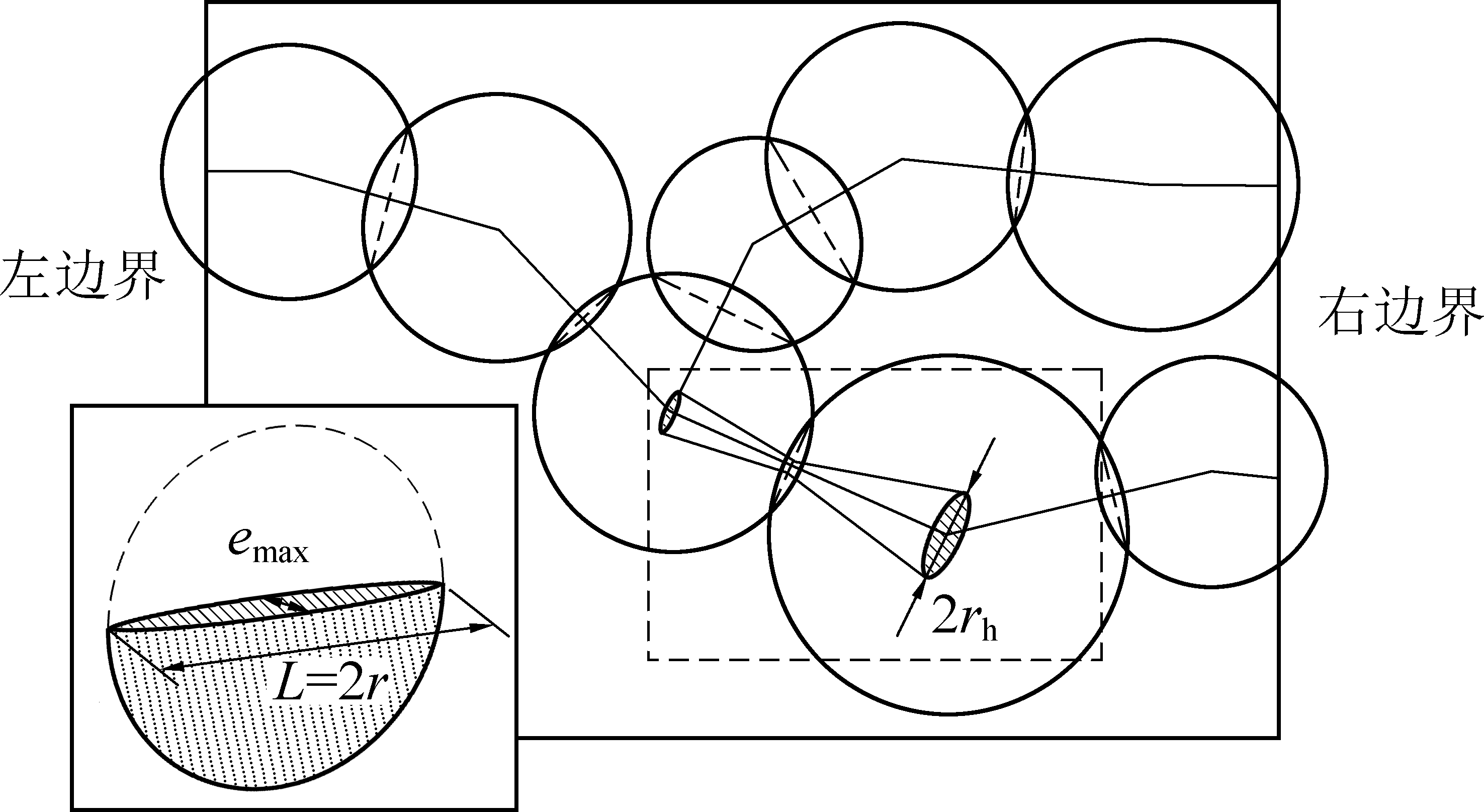
图2 等效管道模型示意
Fig.2 Schematic of equivalent pipeline model
通过上述等效模型,可以生成等效管网模型,如图3所示。

图3 三维等效管网模型
Fig.3 3D equivalent pipe network model
为消除边缘效应,在初始模型(50 m×50 m×50 m)中切割25 m×25 m×25 m大小的模型。在稳态流动条件下,取入口平面(X=12.5 m,X、Y、Z为三维坐标系)的水头为1,出口平面(X=37.5 m)的水头为0,其余边界不透水,可以得到沿X轴方向(左至右方向)的等效管道的水头分布(图4a)和速度分布(图4b)。类似地,还可以获得沿Y轴(前后方向)和沿Z轴(上下方向)的水头分布和速度分布。
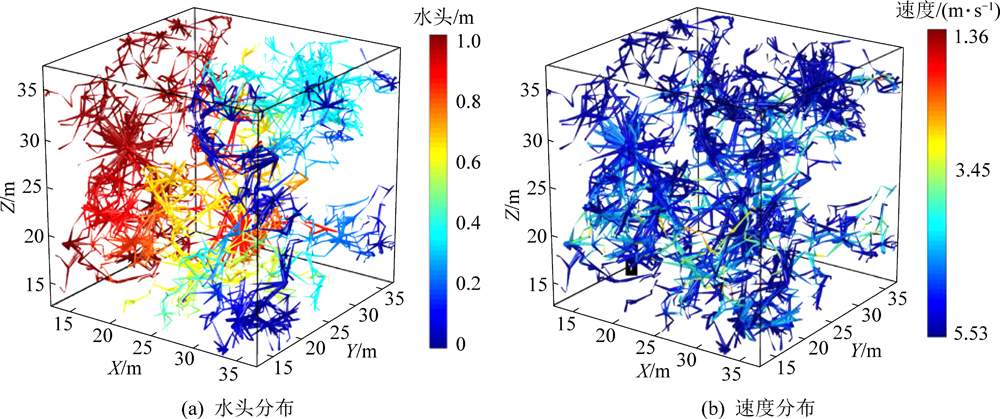
图4 等效管道连通路径网络中的稳态流动
Fig.4 Steady state flow in equivalent pipeline connected path network
假设裂隙中的水体是不可压缩的,等效渗透系数是指渗透断面上单位面积的流量。由于岩土渗透率的差异,裂隙岩体渗流段和渗流路径上的等效渗透系数也有很大差别;根据达西定律,采用反映实际路径渗透特性的等效路径渗透系数,即各连通路径上各渗透段渗透系数的综合值。
对北山核废料库区典型露头的部分裂缝进行切割后发现,切割出的新鲜裂缝,部分具有特定方位的裂缝属于张开型(图5a)。同时,在一定方向上,有些裂缝属于不导水的胶结闭合型(图5b),因此将裂缝分为导水型和堵水型,只有堵水型参与裂缝网络的形成。根据甘肃省新昌地区的场地规律,在测区(露头)进行裂隙监测,其等效渗透系数与岩石基质相同,即10-9m/s。

图5 北山核废料库区实地调查
Fig.5 Field investigation of Beishan nuclear waste area
为了进一步研究裂缝的渗流特征,分别从左边界(X=12.5 m)、沿X轴到右边界末端(X=37.5 m)提取和可视化具有最短渗流时间(图6a)和最短距离(图6b)的连通路径。
其中图6a为最短时间路径,共有108条连通路径,最大渗透系数为1.06×10-6 m/s;图6b为最短距离路径,共有87条连通路径,最大等效渗透系数为3.25×10-7 m/s。此外,图6显示了在初始边界上有更多的路径,当它们接近结束边界时,路径的数量越少,可以直观地得出,连通距离最短的路径不一定是渗透系数最大的路径,也不是时间最短的路径。还可以得出结论,最短时间连接路径具有最大的等效路径渗透系数,这与实际情况相符。
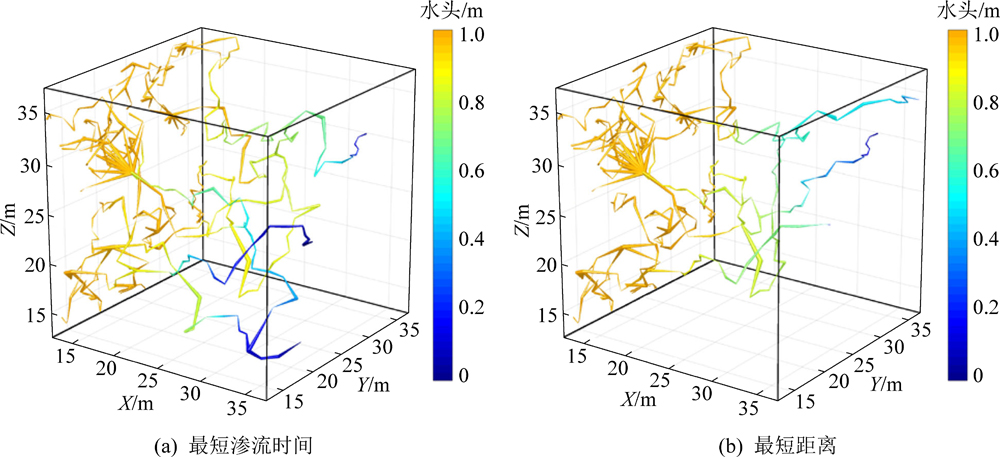
图6 可视化的连通路径
Fig.6 Visual connectivity path
对于图3中的等效管道连接路径网络,搜索589条从左到右的断开连接路径,对这些等效路径渗透系数进一步统计结果表明:当渗流管网未胶结时,90%的等效路径渗透系数大于10-7 m/s,主要在10-4~10-3 m/s,等效路径渗透系数平均值为10-3 m/s(图7a)。此外,当渗流管网中存在胶结时,97%的等效路径渗透系数小于10-7 m/s,主要在10-9 ~10-7 m/s,平均路径渗透系数为10-7 m/s(图7b),模拟结果在露头附近钻孔测试值(BS35和BSQ05[22])的范围内。

图7 等效路径渗透系数累积分布
Fig.7 Cumulative distribution of equivalent path permeability coefficient
计算了不同尺寸的DFN模型在X轴、Y轴和Z轴正方向(分别对应于地理位置的东、北和自上而下)的等效渗透系数(图8)。

图8 等效渗透系数随DFN模型尺寸的变化情况
Fig.8 Change of equivalent permeability coefficient with DFN model size
由图8可知,当模型尺寸较小时,3个方向对应的等效渗透系数相差较大,说明在该尺寸下的计算结果不具备代表整体特征的能力。随着模型尺寸的逐渐增大,等效渗透系数在3个方向上的波动逐渐减小,结果表明,当模型尺寸大于25 m×25 m×25 m时,各方向的渗透系数随尺寸的增大变化不大,因此,裂隙系统的表征单元体积尺寸约为25 m×25 m×25 m,模型在上部和下部具有最大的等效渗透系数,为10-7 m/s,最小的为东向,为10-8 m/s。
2 渗透张量的计算
通过二维平面渗透系数拟合二维椭圆,利用得到的三维空间方向等效渗透系数拟合椭球体。为避免等效渗透系数Ki极小而造成计算误差,将Ki转换为![]() 并保持原来的方向,然后用最小二乘法拟合已知的椭球体,拟合结果如图9所示。
并保持原来的方向,然后用最小二乘法拟合已知的椭球体,拟合结果如图9所示。
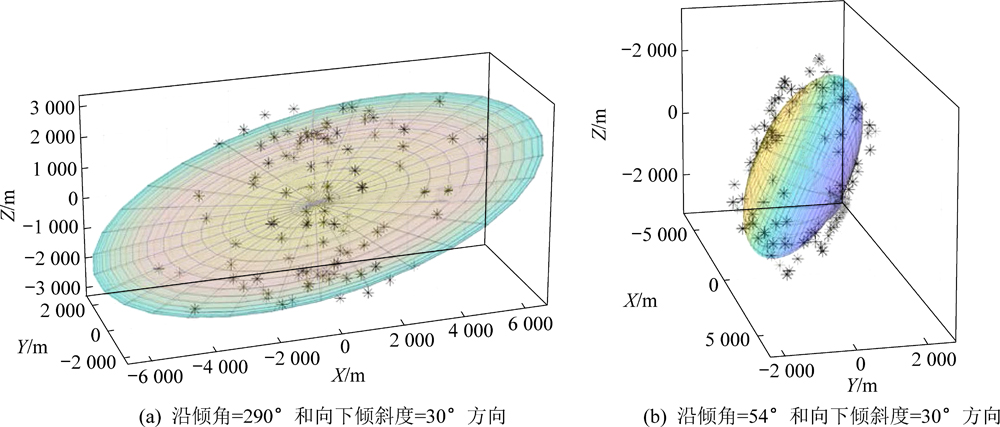
图9 三维空间中的渗透率椭球体
Fig.9 Permeability ellipsoid in 3D space
由图9可得,102个方向的空间渗透系数可以拟合到1个空间椭球体上,结果表明,等效连续体法可应用于选定的研究区(露头),为工程中解决相关问题提供了方法。对于拟合后的椭球体,用最小二乘法求其最小值,用极值原理得到参数A、B、C、D、E、F的线性方程组,其中A~F为定义一个球面所需要的参数(AX2+BY2+CZ2+DXY+EXZ+FYZ=1),各参数为A=0.93×10-7,B=3.22×10-7,C=1.43×10-7,D=2.04×10-7,E=-1.06×10-7,F=-1.43×10-7。
由拟合椭球体得到的勘察区(露头)裂隙岩体渗透率主值及主方向见表1。
表1 拟合椭球体得到的渗透率主值和主方向
Table 1 Principal values and directions of permeability obtained by fitting ellipsoid

方向渗透率主值/10-7(m·s-1)倾向/(°)倾角/(°)X0.252117.4568.72Y1.340331.3732.19Z4.863208.6576.53
由表1可知,求解的渗透率与XU[15]相差不大,误差在允许范围内。通过拟合椭球体,最大渗透率方向(倾角为208.65°)与最小渗透率方向(倾角为117.45°)之差为91.2°,接近90°。
3 结 论
1) 在实地调查中,对露头地表暴露部分裂缝进行一定深度的切割,使新鲜裂缝暴露。发现,某一走向范围内的部分裂缝属于张开型裂缝,另一走向范围内的裂缝属于胶结闭合型裂缝。这一发现为合理分析裂缝及整个地区的渗流特征提供了参考。
2) 为了合理方便地研究复杂裂隙网络中裂隙的渗流特性和岩体整体渗透特性,采用一定厚度的圆盘模拟裂隙面,将其等效为变直径三维管网模型。提出了等效路径渗透系数的概念,以客观地研究裂隙岩体渗流路径的渗透特性。当单个渗流路径连通性好且裂缝中没有杂质时,等效渗流速度可达10-3 m/s,EPC的量级约为10-2 m/s,反之,如果某些裂缝胶结,即使没有水流,等效渗流速度也可低至10-10 m/s,等效路径渗透系数的平均值的量级约为10-7 m/s,说明胶结裂隙对岩体渗透率的影响很大。
3)在离散断裂网络模型的基础上,通过改变模型的大小,判断研究域具有代表整个局部域的代表性基本体,其大小约为25 m×25 m×25 m,得到了该区的空间渗透率张量(包括渗透率主值和主方向),该预测结果在WANG[22]的钻孔数据范围内,表明预测结果可为今后相关工程提供参考。
[1] CHEN S,FENG X,ISAM S. Numerical estimation of rev and permeability tensor for fractured rock masses by composite element method[J]. International Journal for Numerical and Analytical Methods in Geomechanics,2010,32(12):1459-1477.
[2] 严松宏. 地下结构随机地震响应分析及其动力可靠度研究[D].西安:西南交通大学,2003:15-32.
[3] 石智军,姚 克,姚宁平,等,我国煤矿井下坑道钻探技术装备40年发展与展望[J].煤炭科学技术,2020,48(4):1-34.
SHI Zhijun,YAO Ke,YAO Ningping,et al. Development and rospect of underground tunnel drilling technology and equipment in China for 40 years[J]. Coal Science and Technology,2020,48(4):1-34.
[4] 张平松,许时昂,郭立全,等.采场围岩变形与破坏监测技术研究进展及展望[J].煤炭科学技术,2020,48(3):14-48.
ZHANG Pingsong,XU Shiang,GUO Liquan,et al. Research progress and prospect of monitoring technology for deformation and failure of surrounding rock in stope[J]. Coal Science and Technology,2020,48(3):14-48.
[5] GOC R L,DREUZY J R D,DAVY P. An inverse problem methodology to identify flow channels in fractured media using synthetic steady-state head and geometricaldata[J]. Advances in Water Resources,2010,33(7):782-800.
[6] HANEBERG W C. Using close range terrestrial digital photogrammetry for 3-d rock slope modeling and fracture mapping in the unitedstates[J]. Bulletin of Engineering Geology and the Environment,2008,67(4):457-469.
[7] NEUMAN S P. Trends,prospects and challenges in quantifying flow and transport through fracturedrocks[J]. Hydrogeology Journal,2005,13(1):124-147.
[8] GUO L,LI X,ZHOU Y,et al. Generation and verification of three-dimensional network of fractured rock masses stochastic discontinuities based on digitalization[J]. Environmental Earth Sciences,2015,73(11):7075-7088.
[9] KARRA S O,MALLEY D,HYMAN J,et al. Modeling flow and transport in fracture networks using graphs[J]. Physical Review,2018,97(3):33-40.
[10] WANG M,KULATILAKE Phsw,UM J,et al. Estimation of rev size and three-dimensional hydraulic conductivity tensor for a fractured rock mass through a single well packer test and discrete fracture fluid flow modeling[J]. International Journal of Rock Mechanics and Mining Sciences,2002,39(7):887-904.
[11] TSANG Y,TSANG C. Flow channeling in a single fracture as a two-dimensional strongly heterogeneous permeable medium[J]. Water Resources Research,1989,25(9):2076-2080.
[12] CACAS M,LEDOUX E,MARSILY Gd,et al. Modeling fracture flow with a stochastic discrete fracture network:calibration and validation:1. The flow model[J]. Water Resources Research,1990,26(3):479-489.
[13] NORDQVIST A,TSANG Y,TSANG Cf,et al. A variable aperture fracture network model for flow and transport in fractured rocks[J]. Water Resources Research,1992,28(6):1703-1713.
[14] CLEMO T,SMITH L. A hierarchical model for solute transport in fracturedmedia[J]. Water Resources Research,1997,33(8):1763-1784.
[15] GYLLING B. Development and applications of the channel network model for simulations of flow and solute transport in fracturedrock[D]. Stockholm:Royal Institute of Technology,2003:22-40.
[16] BRUDERERWENG C,COWIE P,BERNABÉ Y,et al. Relating flow channelling to tracer dispersion in heterogeneous networks[J]. Advances in Water Resources,2004,27(8):843-855.
[17] XU C,FIDELIBUS C,DOWD P. Realistic pipe models for flow modelling in discrete fracturenetworks[J]. International Discrete Fracture Network,2014,33(10):923-945.
[18] BAGALKOT N,KUMAR Gs. Numerical modeling of two species radionuclide transport in a single fracturematrix system with variable fracture aperture[J]. Geosciences Journal,2016,20(5):627-638.
[19] WANG P,CAI M,REN F,et al. A digital image-based discrete fracture network model and its numerical investigation of direct shear tests[J]. Rock Mechanics and Rock Engineering,2017,50(7):1801-1816.
[20] DESSIRIER B,TSANGCf,NIEMI A. A new scripting library for modeling flow and transport in fractured rock with channel networks[J]. Computers & Geosciences,2018,111(2):181-189.
[21] KULATILAKE P,WU T H. The density of discontinuity traces in sampling windows[J]. International Journal of Rock Mechanics and Mining Sciences,1984,21(6):345-347.
[22] WANG J,CHEN L,SU R,et al. The beishan underground res-earch laboratory for geological disposal of high-level radioactive waste in china: planning,site selection,site characterization and in situ tests[J]. Journal of Rock Mechanics & Geotechnical Engineering,2018,10(3):411-435.
