移动扫码阅读
移动扫码阅读
近年来，瞬变电磁法在我国地质勘探领域取得了很大的发展，尤其在金属矿勘探、煤田地质勘探、水文地质勘探、工程地质勘探等领域取得了广泛的应用[1-3]。那么如何提高探测深度以及在极限探测深度范围内提高探测精度又开始成为亟待突破的问题。一直以来，对于瞬变电磁法，关断时间(以及采样延时)影响及校正的研究较多。于生宝等[4]通过对发射电流关断时间影响瞬变电磁法探测结果的推导，对早期瞬变响应阶跃关断与线性关断的区别进行了分析。杨海燕等[5]对斜阶跃影响校正进行了研究，结果显示，多匝小回线的匝数越多，反演深度可以扩展的范围越大，反演电阻率的精确性可通过减少匝数而提高。
研究普遍认为，发射线框中电流无法迅速关断，形成浅层探测盲区，关断时间持续越长，则形成的浅层探测盲区越大；不仅如此，接近关断时间尾部的信号也会受到关断效应的影响而产生畸变，当然，已有研究可通过校正基本消除该影响。白登海等[6]提出可以通过设备记录的激发场完整衰变曲线，实现对线性和指数关断影响进行精确校正。杨云见等[7]采用经典的马奎特法直接对包含斜阶跃关断时间效应的瞬变电磁资料进行反演，反演结果及计算速度均较为理想。杨海燕等[8]对线性关断和半正弦关断2种关断模式进行了研究，得出，同一关断时间下这两种关断模式对二次场的影响主要表现在“早期”,随采样时间的增加而逐渐减弱。同时,关断时间越长,其影响越向“晚期”延伸；半正弦关断电流对二次场的影响大于线性关断电流。
采样时窗也引起广泛研究，冷胜友等[9]研究认为瞬变电磁法观测时窗的选择与探测效果关系极大：对不同的目标体，选用不同的探测时窗，可取得较好的探测效果；而鲜有对建场时间的研究，或认为非阶跃通电时间对瞬变电磁探测的影响可忽略不计[10]。事实究竟如何，笔者将从瞬变电磁法建场时间的角度对这一问题做详细的论述。通过计算分析，最终建议将瞬变电磁系统固定的建场时间模式，调整为若干个可选档位(或限定区间的人工输入模式)，旨在通过在观测时窗中建立更为精细的激发时间序列，进一步提高瞬变电磁法的探测深度及提高采样效率。当然，影响瞬变电磁法观测效果的因素众多，本文仅从建场时间的角度进行推导。导线通电并在其周围空间建立磁场是“瞬间”的过程，那么建立稳恒磁场又需要多少时间？稳恒磁场建立后何时开始“取样”？众所周知，为了便于对电信号分析，需要进行傅里叶变换[11-12]。
电工学电气学中，常将周期为T(=2π/ω)的双极性矩形波函数用一系列以T为周期的正弦函数Ansin(nωt+φn)组成的级数表示为
(1)
式中:A0为初始振幅；An为振幅；ω为角频率，rad/s；φn为相位，rad。
将双极性矩形波周期函数按式(1)展开的物理意义是很明确的，这就是把一个比较复杂的周期运动看成是许多不同频率的简谐振动的叠加，电工学上称之为谐波分析。其中常数项A0称为f(t)的直流分量A1sin(ωt+φ1)一次谐波(基波)，则A2sin(2ωt+φ2)，A3sin(3ωt+φ3)，……，依次称为二次谐波，三次谐波，……。
为了方便，把正弦函数Ansin(nωt+φn)按三角公式展开为
Ansin φncos nωt+Ancosφnsin nωt
令a0/2=A0，an=Ansinφn，bn=Ancosφn，ω=π/l(即T=2l)，则式(1)右端可改为
(2)
形如式(2)的级数称之为三角级数，其中，a0，an，bn(n=1，2，3，……)都是常数。
令πt/l=x，则式(2)化为
这就将以2l为周期的三角级数f(t)转换成以2π为周期的三角级数f(x)，即
据三角函数系(1，cos x，sin x，cos 2x，sin 2x，…，cos nx，sin nx，…)中任意2个不相同的函数的乘积在[-π，π]区间积分为零的基本原理，仅保留k=n的分式，an和bn表达式计算结果如下:
(n=0，1，2，…)
(n=1，2，…)
先以特定的矩形波为例：设g(t)是周期为T的周期函数，它在[-T，T)上的表达式为
其函数图形如图1所示。
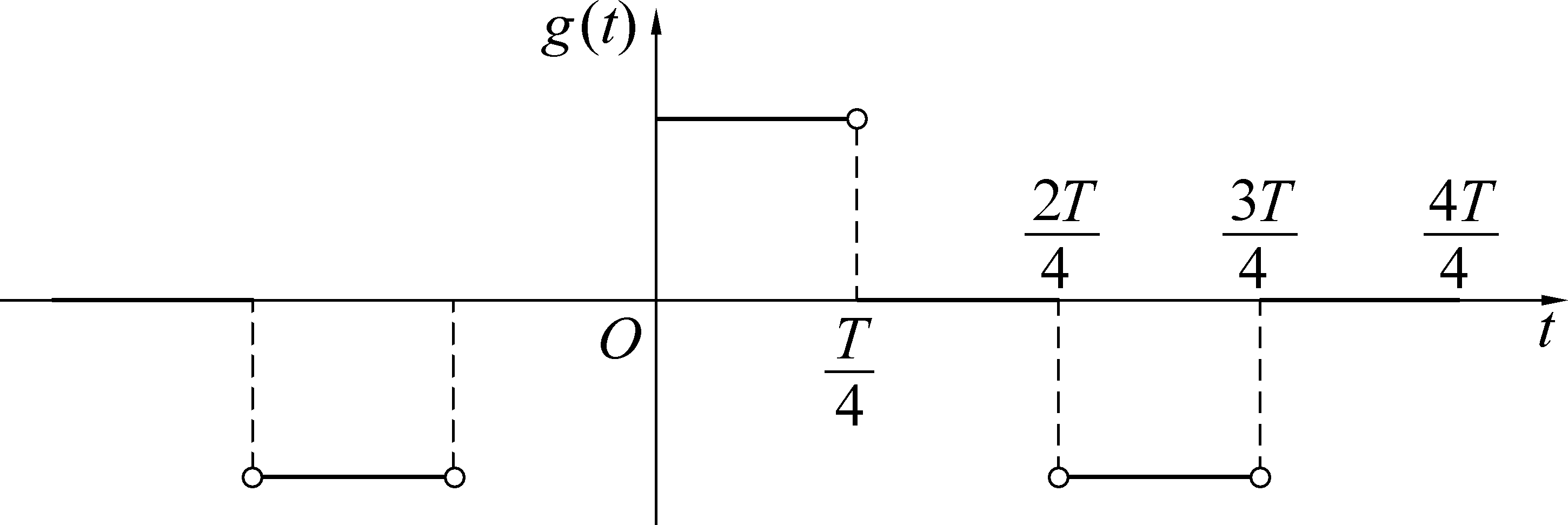
图1 矩形波周期函数
Fig.1 Functional of rectangular periodic wave
经计算得到g(t)的傅立叶级数展开式为
(-∞<t<+∞；t≠0，t=±kT/4,……)
上式表明：矩形波是由一系列不同频率的正弦波叠加而成，这些正弦波的频率依次为基波频率的奇数倍[15-16]。以各型号仪器常用采样频率f=6.25 Hz为例，则T=0.16 s=π/20 s，则T/4=π/80 s。
在正极性(0，T/4)的时域内，对采样起始时间t分别赋值进行计算。分别赋值为
进行计算，g(t)的傅立叶级数展开式简化为
对
进行信号强度采取率计算，得
各项分布如下
853 9+0.007 853 25+0.007 851 96+
0.007 850 03+…+0.000 0196 8)
同理，当
时，计算得f(t)各项分布，将上述计算结果见表1，将不同建场时刻的频谱图绘制成剖面平面图(图2)。
表1 不同建场时刻信号成分极大频率分布
Table 1 Maximum frequency distribution of signal components at different building-field time
f/Hz7992π3992π1992π1312π992π852πt/sπ800π4002π4003π4004π40023π2000
注：由公式f=1/T、T=2π/ω对角频率ω和频率f进行了转换。
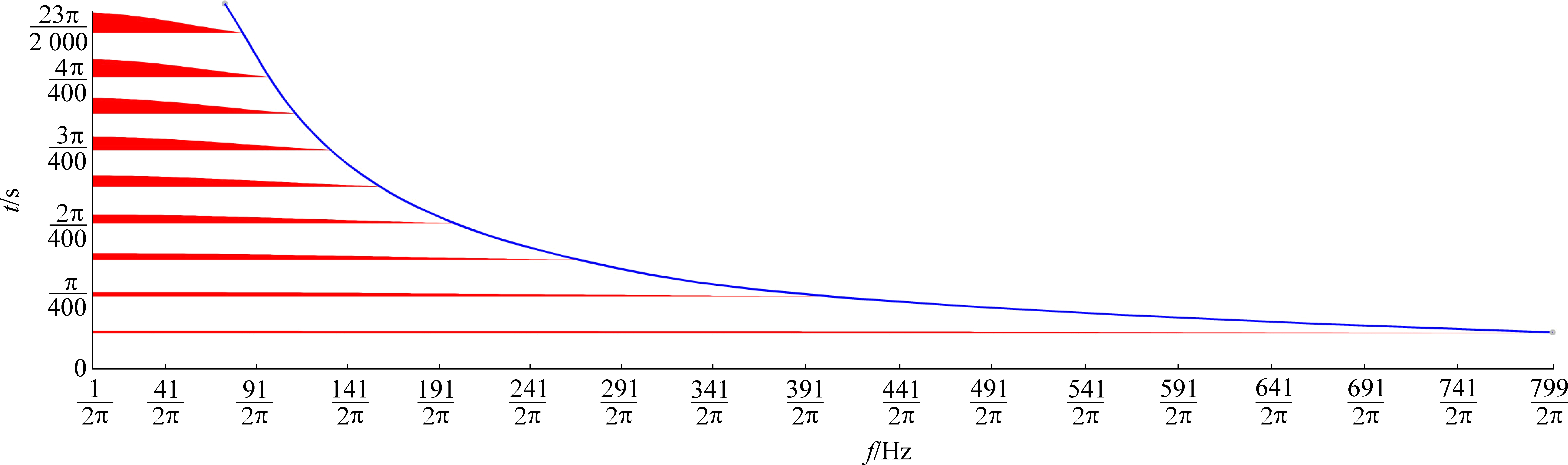
图2 特定建场时刻频谱平剖图
Fig.2 Plane profile of spectrum at certain build-up time
由图2明可知，建场时刻函数与频率极大值呈减函数对应关系，即建场时间越长，频谱中最大频率越小(频带越窄)。对该函数进行推导，令x轴为频率f分布、y轴为建场时刻，可得
(3)
(4)
由图2可以看出，各时刻的信号幅值，在频谱带上，由低频到高频逐渐变小，最大频率为该频率信号幅值接近0且k取整的对应位置处，即式(3)为0，则式中sin(2k-1)t项须为0，则(2k-1)t为最接近π的k取整位置处，可令(2k-1)t=π，可得k=π/(2t)+1/2，进一步得fmax=ω/(2π)=(2k-1)/(2π)=1/(2t)，则最终可得频率极值和建场时间的对应函数关系式为
fmax=1/(2t)=0.5t-1
(5)
显然，式(5)为幂函数，绘制有效建场时段内，频率极值随建场时间的变化曲线，如图3所示。
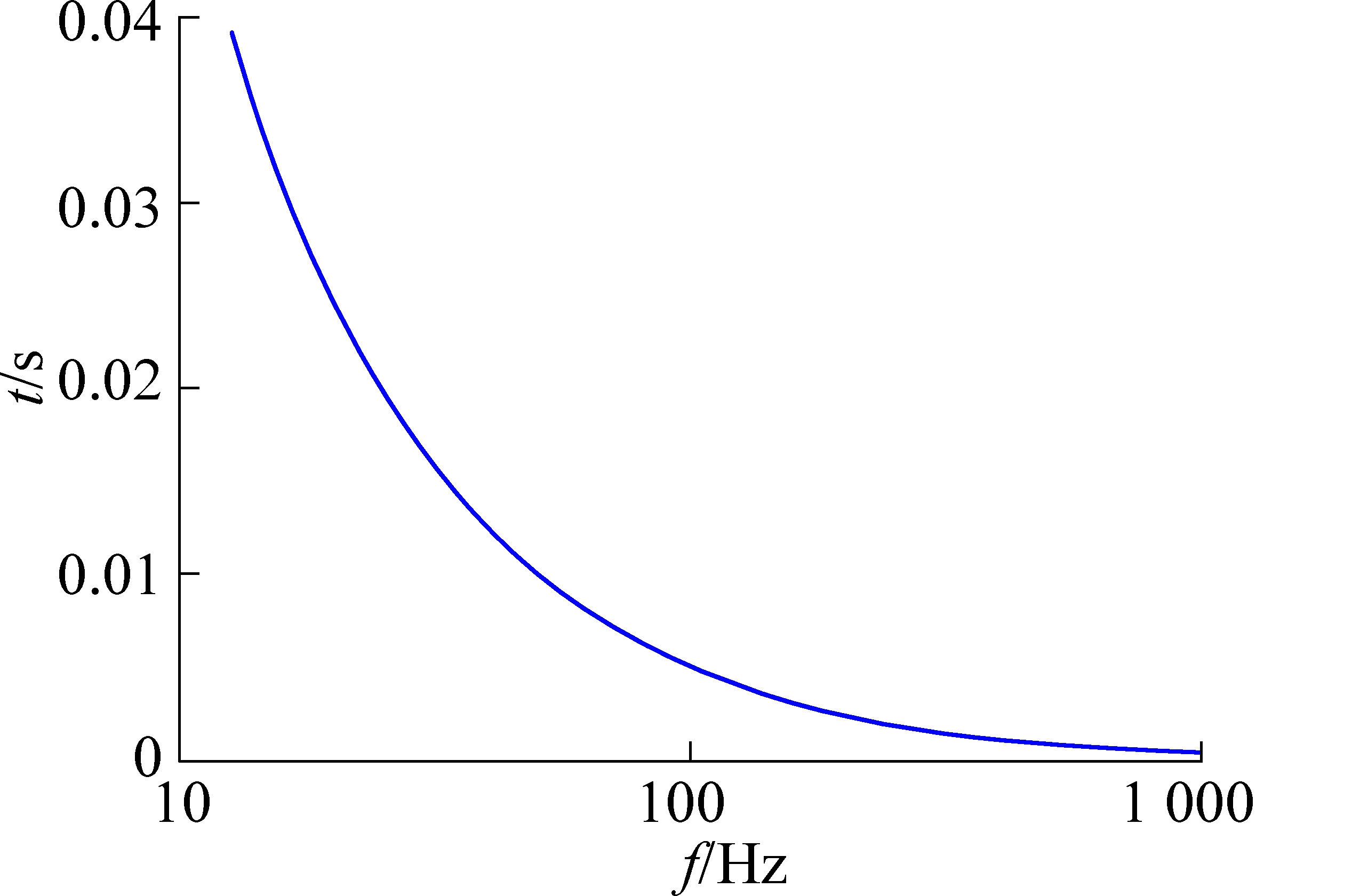
图3 频率极值随建场时间的变化曲线
Fig.3 Function curve of maximum frequency changing with building-field time
进一步推导，在有效建场时域内，特定时刻频谱频率幅值随频率 变化的函数关系，令x轴为频率分布，y轴为信号幅值，列出如下函数关系为
(6)
(7)
式(6)、式(7)联立可得
(8)
在有效建场时段，给定任意时刻，可算出频率幅值随频率的频谱分布曲线，对式(8)以t=π/400 s时刻为例，绘制曲线如图4所示。
图4 t=π/400 s时刻频谱曲线和信号幅值衰减比率曲线
Fig.4 Function curves of frequency spectrum and signal amplitude decay ratio at certain time t=π/400 s
关于 “时段”，即分为最早时刻和最晚时刻，最早时刻计算如下：
趋肤深度
平均电阻率ρ以100 Ω·m计，以频率域测深法中可控源音频大地电磁法的常用最大频率8 192 Hz为例[17]，计算得，其对应的趋肤深度为56 m，该深度已经与常规地面瞬变电磁法浅层盲区覆盖深度[18-20]相近(这里不做精确计算)，所以不必再追求更大频率。由式(5)计算得，该频率对应时刻为61.0 μs。同理，最晚时刻计算如下：以800 m为常规瞬变电磁探测较大深度计，平均平均电阻率ρ同样以100 Ω·m计，计算可得频率为39.5 Hz，进一步由式(5)计算得，该频率对应时刻为12.7 ms。
由上述计算可得，常规瞬变电磁勘探可根据不同的探测深度要求将建场时段选在61.0 μs～12.7 ms，受限于瞬变电磁法浅层盲区，不必为了获取更丰富的频率组分而追求低于61.0 μs的建场时间；同样，受限于常规瞬变电磁勘探深度的能力，亦不必将建场时间选择高于12.7 ms。
1)在(0，T/4)的有效建场时段内，发射线框始终保持恒定的激发场，这个激发场是由若干个不同频率所给出不同幅值的信号叠加而成，不同时刻频谱具备如下规律：建场时间越长，频带越窄，且向低频集中，将无法满足浅层探测；反之，建场时间越短，频带越宽，理论上可以达到无限宽，但受限于仪器发展水平，无法在无穷短的时间内建立稳恒电流。当然也并不追求无穷短的建场时间，因为虽然频带极宽，但各频率对应信号幅值均极小，由浅到深均无法起到激发的作用。通过量化计算，最终将建场时刻锁定在通电后61.0 μs～12.7 ms。
2)有效建场时段的任意时刻，各频率信号幅值随着频率的增高而逐渐减小，前1/3的低频段内，信号幅值衰减到极大值的83%；前2/3的频段内，信号幅值衰减到极大值的47%。
3)将建场从特定采样频率(对称式1∶1“占空比”)中分离出来，建立占空比由1∶1向1∶8过度的若干个非对称式“发射-观测”序列，设想生产非对称式“占空比”采样模式的样机，以实现更合理高效的瞬变电磁数据采集。
[1] 牛之琏.时间域电磁法原理[M].长沙：中南大学出版社,2007：13-15.
[2] 蒋邦远.实用近区磁源瞬变电磁法勘探[M].北京：地质出版社,1998：9-12.
[3] DZT 0187-2016 ,地面瞬磁性源瞬变电磁法技术规程[S].
[4] 于生宝,王 忠,嵇艳鞠,等.瞬变电磁法浅层探测技术[J].电波科学学报,2006,21(2):284-287.
YU Shengbao,WANG Zhong,JI Yanju,et al.Time domain transient electromagnetic shallow prospecting[J].The Chinese Journal of Radio Science,2006,21(2):284-287.
[5] 杨海燕,岳建华,李锋平.斜阶跃电流激励下多匝小回线瞬变电磁场延时特征[J].地球物理学报,2019,62(9):3615-3628.
YANG Haiyan,YUE Jianhua,LI Fengping.The decay characteristics of transient electromagnetic fields stimulated by ramp step current in multi-turn small coil[J].Chinese Journal of Geophysics,2019,62(9):3615-3628.
[6] 白登海,MAXWELL Meju.瞬变电磁法中两种关断电流对响应函数的影响及其应对策略[J].地震地质,2001,23(2):245-251.
BAI Denghai,MAXWELL Meju.The effect of two types of turn-off current on TEM responses and the correction techniques[J].Seismology and Geology,2001,23(2):245-251.
[7] 杨云见 ,王绪本 ,何展翔 .考虑关断时间效应的瞬变电磁一维反演[J].物探与化探,2005,29(3):234-236.
YANG Yunjian,WANG Xuben,HE Zhanxiang.1D inversion of TEM data in consideration of ramp time effect[J].Geophysical &Geochemical Exploration,2005,29(3):234-236.
[8] 杨海燕,岳建华.瞬变电磁法中关断电流的响应计算与校正方法研究[J].地球物理学进展,2008,23(6):1947-1952.
YANG Haiyan,YUE Jianhua.Research on response calculation and correction technique of turn-off current in the transient electromagnetic method[J].Progress in Geophysics,2008,23(6):1947-1952.
[9] 冷胜友,闫 述.煤田水文地质勘探中瞬变电磁法的观测时窗和观测区域[J].煤田地质与勘探，2005,33(S1):184-186.
LENG Shengyou,YAN Shu.Observation time window and area in transient electromagnetic field method for coalfield hydro-geologic exploration[J].Coal Geology &Exploration,2005,33(S1):184-186.
[10] 冯晓兰.可实现TEM发射电流下降沿的线性及稳定性技术[J].地质与勘探,2002,38(S1):126-128.
FENG Xiaolan.Realizing TEM emission current back edge’s linear &stability technology [J].Geology and Exploration,2002,38(S1):126-128.
[11] 陈明生.关于频率电磁测深几个问题的探讨(八)：频率电磁测深与瞬变电磁测深的关系[J].煤田地质与勘探,2015,43 (1):81-85.
CHEN Mingsheng.On the relationship between the frequency electromagnetic sounding with the transient electromagnetic sounding(part 8)[J].Coal Geology &Exploration，2015，43(1)：81-85.
[12] 傅良魁.电法勘探教程[M].北京：地质出版社,1983：6-8.
[13] 李 貅,宋建平,马 宇，等.基于小波分析的TEM信号提取[J].煤田地质与勘探,2005,33 (2):72-75.
LI Xiu,SONG Jianping,MA Yu,et al.The abstract of TEM signal based on the wavelet analysis[J].Coal Geology &Exploration,2005,33(2):72-75.
[14] MCNEIL J D.Geonics Limited Technical Note TN-7：application of transient electromagnetic techniques[R].Mississauga:Electromagentic Geophsical Instrument,1980:13-15.
[15] 王 忠,嵇艳鞠,林 君,等.全程瞬变电磁系统的浅层探测实验研究[J].吉林大学学报(地球科学版),2005,35(S1):95-98.
WANG Zhong,JI Yanju,LIN Jun,et al.Study of the experiments of all-time transient electromagnetic system for shallow survey[J].Journal of Jilin University(Earth Science Edition),2005,35(S1):95-98.
[16] Enterprise Technical Cente.Geoex SIROTEM-Ⅱ system opera-tion manual[R].Post Wakefield:Geex Pty Ltd，1980.
[17] 薛国强.论瞬变电磁测深法的探测深度[J].石油地球物理勘探,2004,39(5):575-578.
XUE Guoqiang.On surveying depth by transient electromagnetic sounding method[J].Oil Geophysical Prospecting,2004,39(5):575-578.
[18] 薛国强,宋建平,阎仕农,等.大回线源瞬变电磁法最小探测深度的分析与估算[J].工程勘察,2004(2):63-65.
XUO Guoqiang,SONG Jianping,YAN Shinng,et al.Study and calculation on the minimum detecting depth with method of large-loop transient electromagnet[J].Geotechnical Investigation &Surveying,2004(2):63-65.
[19] PATRA H P,MALLICK K.Time-varying geo-electric soundings[R].Amsterdam:Elsevier Scientific Publishing Company,1980.
[20] 岳建华,杨海燕,邓居智.层状介质中地下瞬变电磁场全空间效应[J].地球物理学进展,2012,27(4):1385-1392.
YUE Jianhua,YANG Haiyan,DEGN Juzhi.Whole-space effect on underground transient electromagnetic field in layered media[J].Progress in Geophysics,2012,27 (4):1385-1392.