
移动扫码阅读
随着煤炭开采速率的不断提升,矿井水害逐渐成为威胁煤炭安全开采的主要因素之一。统计表明,我国受矿井水害威胁的煤炭资源储量占探明总储量的27%[1]。因此,如何有效治理矿井水害成为现阶段研究的热点和难点问题。矿井水害的主要治理手段有疏干排水、疏堵结合、注浆堵水3种。注浆堵水技术在矿井水害防治工程中被大量运用,该技术对保护水资源和保证矿区持续发展具有重要意义[2-3]。
目前,国内外学者从理论分析、室内试验及数值模拟等方面对注浆堵水工程中浆液扩散规律进行了大量的研究。文献[4]中提到MAAG、RAFFLE等基于达西定律,首先提出了牛顿流体浆液的球形扩散理论与柱形扩散理论,得到了浆液扩散半径、注浆时间及注浆压力之间的关系。随后非牛顿流体的浆液扩散理论得到发展,杨秀竹等[5-6]推导了宾汉体及幂律流体浆液在渗透注浆过程中的扩散半径公式。SAADA[7]、CHUPIN等[8]通过理论分析建立了考虑渗滤效应的多孔介质渗透扩散模型,研究了渗滤效应对浆液扩散范围的影响。隋旺华[9-10]、俞文生等[11]通过理论推导建立了单裂隙动水注浆浆液扩散模型,并结合室内试验与数值计算的方法研究了浆液在单裂隙中的扩散规律。李术才[12-14]、张庆松等[15-17]基于浆液黏度的时变性,通过建立理论模型,并结合室内注浆模拟试验与数值模拟的方法研究了浆液在不同介质中的扩散规律,对隧道开挖工程中指导突涌水灾害治理有一定的实践意义与参考价值。刘泉声[18]、黄耀光等[19]采用注浆的方法对深部巷道围岩进行注浆加固,对浆液扩散机理进行了深入探讨,并将注浆工艺应用到现场注浆工程。刘健等[20]采用数值模拟软件,分别研究了水泥浆液在静水条件和动水条件下在平面裂隙中的扩散规律。目前,对于地下工程中含水层帷幕注浆浆液扩散规律的研究较少。
煤矿开采过程中由于过度抽排地下水,导致地下水位严重下降,破坏生态环境。采用帷幕注浆在地下形成一道帷幕墙,将煤矿开采区与地下水隔离,便可大幅度降低抽排水费用,避免开采区的地下水资源和水环境受到破坏[21]。在上述研究基础上,针对地下含水层帷幕注浆过程中存在的问题,室内开展现场注浆材料的物理性能测试,建立含水层中浆液扩散的数学模型,并通过数值计算与理论计算得到浆液的扩散范围,研究浆液在含水层中的扩散规律,旨在为帷幕墙建造过程中注浆孔距及相关参数的选取提供参考和理论指导。
朱仙庄煤矿井田北侧分布一层由灰岩砾石、角砾组成,钙质胶结的侏罗系底部地层,俗称“五含”。现有的勘探表明,“五含”直接压覆于煤系地层,在采掘活动影响下,“五含”中的水及参与补给的太、奥灰水通过导水通道进入矿井造成水害。朱仙庄矿曾发生过工作面顶板“五含”突水事故,这已严重威胁下伏8煤的安全开采,成为制约矿井安全生产的主要障碍。
据探查统计,“五含”下伏8煤包括6采区、8采区、10采区和12采区,煤炭资源总储量约1 800万t,探明可采储量约1 000万t。8煤是朱仙庄煤矿开采的主采煤层,关系到矿井的总体布局和经济效益。经研究讨论,认为利用现有技术手段对“五含”进行大面积注浆治理或井下直接疏干等措施,施工难度大,成本高,且会产生新的安全威胁,无法彻底根治水害。基于多方因素考虑,最终确定对朱仙庄矿“五含”水害采用帷幕截流治理方案。朱仙庄矿“五含”帷幕截流治理工程帷幕墙展布,如图1所示。工程设计在地表下建造一条防渗帷幕墙,帷幕墙建成后既能较好的保护地下水资源,又能大幅度的降低“五含”水害治理的工程造价,使8煤能安全、环保和经济的开采。

图1 朱仙庄矿“五含”帷幕截流治理工程帷幕墙展布示意
Fig.1 Drawing of curtain wall distribution of ‘fifth aquifer’curtain closure control project in Zhuxianzhuang Coal Mine
但建造帷幕墙需要考虑浆液在含水层中的扩散机制,注浆压力及浆液在含水层中的扩散范围决定着帷幕墙建造的质量。因此,研究含水层中浆液的扩散范围及注浆压力对建造帷幕墙显得尤为重要。
浆液的流动性、结石率、凝结时间及抗压强度等性能需满足朱仙庄煤矿“五含”帷幕墙建设要求。单液水泥浆因具有成本低、结石率高、抗渗性强、稳定性强等优点,在解决各种不同水文地质条件下的堵水加固和防渗问题等方面得到较为广泛的应用。
试验材料为现场注浆使用的32.5R复合硅酸盐水泥。结合现场注浆的要求,试验中单液水泥浆的水灰比设置为0.6、0.8、1.0、2.0、3.0五种,研究不同水灰比条件下的浆液性能。浆液的凝结时间采用标准法维卡仪测定;采用RST流变仪测试不同水灰比条件下浆液黏度;使用标准试验模具制备尺寸为160 mm×40 mm×40 mm试样,按照标准GB/T 17671—1999测试试样不同龄期抗压强度;浆液结石率按照标准JC 313—2009进行,试验仪器如图2所示,部分试验照片如图3所示。

图2 试验测试仪器
Fig.2 Testing instrument

图3 浆液性能试验测试
Fig.3 Testing of slurry performance
采用上述试验仪器完成现场注浆材料的性能测试,具体的试验结果见表1。表1给出了不同水灰比下单液水泥浆物理参数,凝结时间、黏度及密度等因素决定着浆液的可注性,抗压强度与结石率表征浆液的强度特征。现场注浆过程中,可根据表1中水泥浆液性能参数,并按照地层类型的不同选取相应水灰比的浆液以满足现场注浆要求。水灰比1∶1的浆液在现场帷幕注浆工程中经常被采用,文中研究帷幕墙建造过程中浆液在含水层中的扩散范围,数值计算选取水灰比1∶1的浆液进行相关分析。
表1 注浆材料性能参数
Table 1 Performance parameters of grouting materials
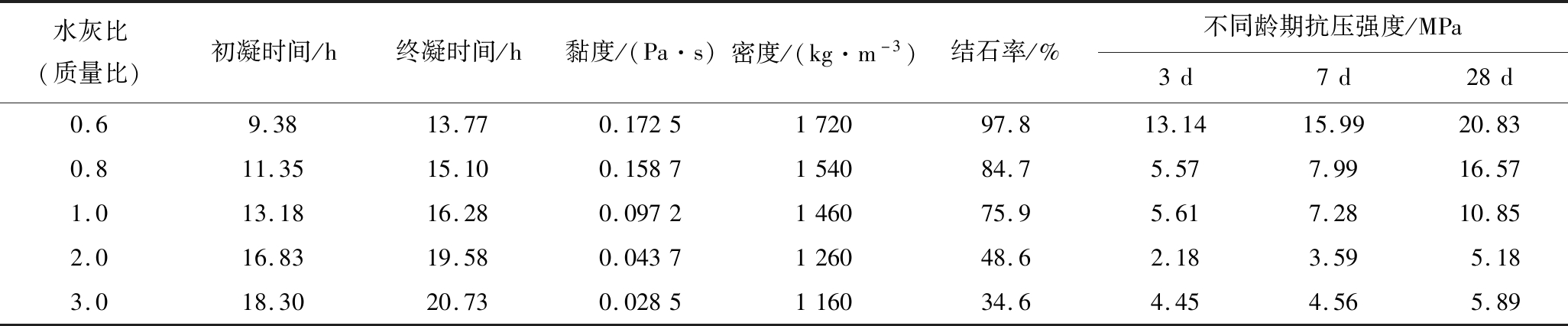
水灰比(质量比)初凝时间/h终凝时间/h黏度/(Pa·s)密度/(kg·m-3)结石率/%不同龄期抗压强度/MPa3d7d28d0.69.3813.770.1725172097.813.1415.9920.830.811.3515.100.1587154084.75.577.9916.571.013.1816.280.0972146075.95.617.2810.852.016.8319.580.0437126048.62.183.595.183.018.3020.730.0285116034.64.454.565.89
含水层中的注浆实质上是浆液驱替地下水的过程。含水层中含有大量的孔裂隙,可将其视为多孔介质,在外力的作用下浆液注入含水层,实际上是浆液与地下水在多孔介质中的流动,且该流动属于两相流的范畴。选取水灰比1∶1的浆液与地下水都属于牛顿流体。因此,浆液和地下水在多孔介质中的流动满足连续性方程和运动方程[22]。
浆液在多孔介质中的连续性方程为
∇·(ρsvs)+∂(φρsss)/∂t=0
(1)
水在多孔介质中的质量守恒方程为
∇·(ρwvw)+∂(φρwsw)/∂t=0
(2)
浆液在多孔介质中的运动方程为
vs=-kksr∇p/μs
(3)
水在多孔介质中的运动方程为
vw=-kkwr∇p/μw
(4)
式中:∇为哈密顿算子;ρs、ρw分别为浆液和地下水的密度;vs、vw分别为浆液和地下水的渗流速度;ss、sw分别为浆液和地下水的体积分数;μs、μw分别为浆液和地下水动力黏度;φ为注浆层位的孔隙率;t为注浆时间;ksr、kwr分别为浆液和地下水的相对渗透率,为体积分数的函数;ks、kw分别为浆液和地下水的有效渗透率或相对渗透率;k为介质渗透率。
浆液和地下水中的每种运动用Darcy定律来表示,当其中任意一种的体积分数为100%时,介质本身所固有的渗透率就取决于其对2种流体的渗透率,即
ksr=ks/k,kwr=kw/k
(5)
由浆液、地下水的连续性方程与运动方程,可得浆液与地下水两相流的控制方程为
∂(φρ)/∂t+∇·(-ρ∇pk/μ)=0
(6)
ρ=swρw+ss ρs
(7)
1/μ=swkwr/μw+ssksr/μs
(8)
s=sw+ss=1
(9)
式中:ρ、μ为浆液和地下水混合密度、黏度;s为浆液和地下水的总体积分数;浆液密度和动力黏度均由前述的浆液性能测试试验得到。
采用COMSOL Multiphysics 有限元软件中的流体力学模块模拟浆液在含水层中的扩散过程,数值计算采用二维模型,将含水层视作多孔介质。根据现场帷幕墙建设的需要,建立30 m×30 m的多孔介质数值模型,布置1个注浆孔位于模型的中心,注浆孔直径为152 mm。模型上下边界为无流动边界,左右边界为定压力边界。初始时刻数值模型多孔介质中内充满水,注浆开始后,浆液以一定注浆压力由注浆孔进入多孔介质。数值模型网格剖分及边界条件如图4所示。

图4 数值模型网格剖分及边界条件
Fig.4 Mesh generation and boundary conditions
为研究注浆压力对扩散规律的影响,分别对不同注浆压力的工况进行分析。其中,根据“五含”特征水文参数渗透系数K=0.326~6.840 m/d,取其平均值,定义多孔介质渗透率为k=4.071×10-12 m2。按照现场注浆压力的范围,模型中的注浆压力p分别取4、5、6 MPa,根据“五含”的埋深情况,模型的静水压力p0取1.5、2.0、2.5、3.0 MPa。数值模型计算参数及计算工况见表2、表3。
表2 计算参数
Table 2 Calculating parameters

水灰比(质量比)浆液密度/(kg·m-3)浆液黏度/(Pa·s)水的密度/(kg·m-3)水的黏度/(Pa·s)孔隙率/%1∶114600.097210000.00115
浆水混合区的计算形态采用体积分数的方式表示。根据表3模拟了不同注浆压力及静水压力下共计12种工况下浆液的扩散形态,不同注浆压力及静水压力下,浆液扩散形态具有相似性,选取工况为注浆压力4 MPa、静水压力2 MPa的浆液扩散形态进行分析,如图5所示,t为注浆时间,r为浆液的扩散半径。在数值软件中设置监测点,监测不同时间段下浆液与地下水的混合区,此时监测得到的混合区距离注浆孔之间的长度就是浆液的扩散半径,如图5中,当t=60 h时,数值软件中监测得到浆水混合区距离注浆孔的长度为6.78 m,也即得到浆液扩散半径r为6.78 m。
表3 计算工况参数
Table 3 Calculating working condition parameters

水灰比(质量比)注浆压力/MPa静水压力/MPa介质渗透率/m21∶14、5、61.5、2.0、2.5、3.04.071×10-12
从图5中可看出,浆液扩散形式是以注浆孔为中心的圆形扩散,图中的红色部分表示浆液浓度,体积分数接近100%,蓝色部分表示地下水,浆液体积分数接近0,即地下水的体积分数接近100%。浆液在多孔介质中的扩散范围随着注浆时间的增长逐渐扩大,但随着注浆时间的继续推移,相同间隔时间段下浆液扩散距离的增大幅度逐渐减小,这是因为在注浆后期,浆液逐渐进入多孔介质中,其扩散的阻力逐渐增大,最终当注浆时间达到一定时,浆液的扩散范围逐渐趋于稳定。此外,在静水条件下的浆水混合区较为明显,且宽度基本保持不变,表明静水条件下地下水对浆液的冲刷与分散作用并不十分强烈。

图5 浆液扩散形态
Fig.5 Grout diffusion behavior
为进一步分析注浆压力及静水压力对浆液扩散范围的影响,根据不同工况下的数值模拟结果,建立不同注浆压力下浆液扩散半径随时间的变化曲线,如图6所示。

图6 浆液扩散半径随注浆时间变化曲线
Fig.6 Curves of grout diffusion radius versus grouting time
由图6可知,在不同注浆压力条件下,浆液扩散半径随注浆时间的增加而增大,但这种增长的速度逐渐下降,即浆液扩散半径的变化率越来越小。当注浆时间达到一定时,浆液扩散半径会趋于一个稳定值,此时若继续注浆,浆液扩散范围有限,注浆难度越来越大。不同注浆压力及静水压力下,浆液扩散半径最终趋于稳定,这是因为当注浆压力较小时,浆液扩散需要的时间较长,但随着注浆时间增长,浆液会出现凝结特性,故而浆液扩散距离会随着时间的增长而趋于稳定;当注浆压力较大时,相比注浆压力较小的情况浆液扩散趋于稳定的时间较短,原因在于高压状态下浆液出现凝结特性的时间较早。对数值模拟的数据进行处理后发现,最终稳定后的浆液扩散半径的平均值为10.22 m,由于浆液的扩散呈明显的轴对称规律,因此不同工况下浆液扩散的范围可达到20.44 m。静水压力对浆液扩散半径有较大的影响,同一注浆压力下,随着静水压力的增大浆液扩散相同范围所需的时间增加,如图6a中,当静水压为1.5 MPa时,浆液扩散至10 m处所需时间为120 h,当静水压为2.0 MPa时,浆液扩散至10 m处所需时间为150 h。另外,从图6中可看出,随着注浆压力的增大,静水压力的变化对浆液扩散半径的影响逐渐减小,这是因为注浆压力越大,浆液驱替水的能力越强,在扩散至相同范围时所需的时间越短,从而静水压力的变化对浆液扩散半径的影响逐渐减弱。
为验证数值模拟的正确性,通过理论计算给出浆液扩散半径的理论值,对理论计算与数值模拟结果进行对比分析。水泥浆液经注浆孔进入地下含水层,在数值模拟计算中将含水层视为多孔介质,因此浆液在注浆孔中以渗透的方式注入地下含水层中。在渗透注浆理论中,浆液在多孔介质中的扩散理论公式[23]为
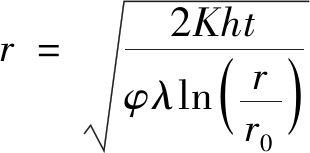
(10)
式中:K为多孔介质的渗透系数,m/s,可由文中多孔介质的渗透率k计算得到;h为注浆压力水头,m;φ为孔隙率;λ为浆液黏度与水的黏度的比值;r0为注浆孔的半径,m。
将理论公式(10)中的各参数赋值后,采用MatLab计算得到浆液渗透扩散半径r,选取部分数值与上述数值模拟所得到的浆液扩散半径进行比较,以静水压力2 MPa为例,建立扩散半径理论计算与数值模拟对比分析曲线,如图7所示。
由图7可知,3种注浆压力下,浆液扩散半径的理论计算值与数值模拟结果差别不大,两者的误差控制小于5%。由此说明所建立的数值模型研究含水层中浆液扩散范围具有一定可靠性。

图7 扩散半径理论计算与数值模拟结果对比
Fig.7 Comparison of theoretical calculation and numerical simulation results of diffusion radius
为确保朱仙庄矿含水层下伏8煤的安全开采,防止井田外“五含”水和奥灰水向井田内补给,在井田北侧和东侧合适区段建立一条帷幕墙,阻隔来自墙外“五含”水向井田内的补给,间接的阻断奥灰水向井田内“五含”的补给。帷幕墙的建造是通过地面打钻钻进至“五含”目标层内,钻孔揭露“五含”储水空间或孔裂隙通道,随后利用地面注浆系统通过钻孔对目标层位进行注浆充填加固,最终形成阻隔地下水进入采煤工作面的帷幕墙体。但在建造帷幕墙的过程中存在诸多问题,例如注浆过程中材料性能、注浆孔间距的选取等。因此,利用本文研究的注浆材料性能及浆液扩散范围,可为现场帷幕注浆工程中注浆材料的选取及注浆孔距的布置提供科学依据。
注浆材料的性能是影响帷幕墙建造的因素之一,其中注浆结石体的强度应满足帷幕墙体的强度要求。表1给出的5种水灰比下的水泥浆液在龄期28 d时的最小抗压强度为5.18 MPa,因此,文中选取的浆液在龄期28 d后的结石体强度能够满足帷幕墙的建设需求。在满足帷幕墙建设强度的基础上,需要考虑浆液的可注性、结石率等因素。根据注浆层位的特征,选取不同水灰比的浆液进行注浆,以满足帷幕墙建设的需求。现场注浆过程中,大都选取水灰比(质量比)1∶1的浆液,这样既能满足浆液结石体的强度又能满足浆液可注性的要求。
浆液扩散范围的研究是注浆工程中注浆孔间距布设的依据。文中数值模拟结果显示,浆液扩散最终稳定后的扩散半径平均值为10.22 m。因此,根据数值模拟计算与理论分析得到的浆液扩散半径,帷幕墙建造中注浆孔间距选为20 m,按照所得的注浆孔间距,设计给出帷幕墙部分钻孔的平面分布示意如图8所示,注浆孔间距和排距均设计为20 m,两排交错布孔,且两排孔的中间位置每80 m设计1个检查孔,建立有效宽度约为40 m的帷幕墙,以阻隔来自帷幕墙外侧“五含”及奥灰水对矿井的补给。
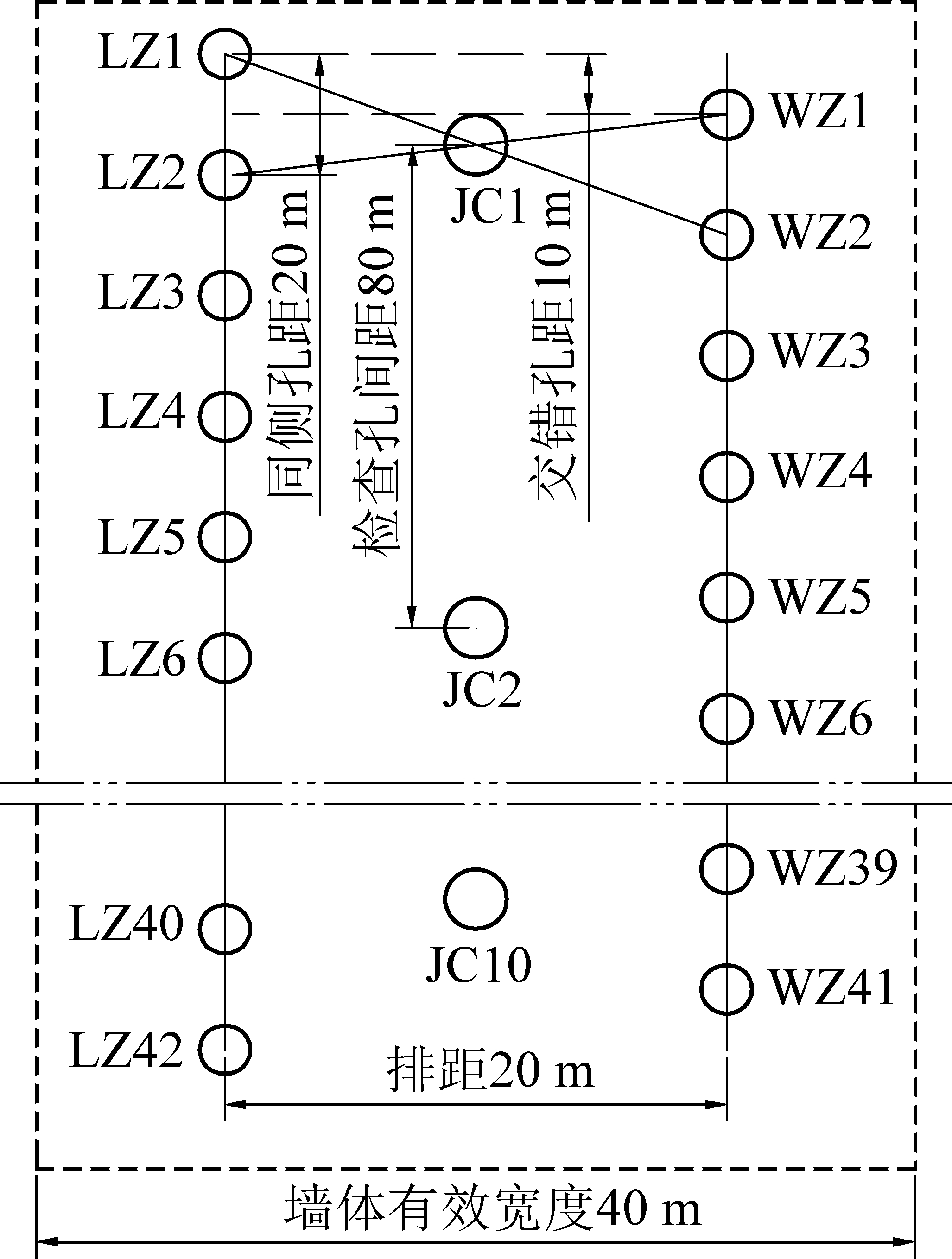
图8 帷幕墙部分钻孔平面分布示意
Fig.8 Plane layout of drilling holes in part of curtain wall
为验证帷幕墙注浆孔距设计的合理性,通过检查孔对受注地层进行岩心采取,若能采集到带有浆液结石体的岩心,则说明浆液能够扩散至设计的距离,进而证明文中设计的注浆孔孔间距合理。现场通过检查孔对受注地层进行取心并密封运往实验室(图9)。

图9 现场取芯试样
Fig.9 Field coring sample
同时得到了含有浆液结石体的岩心,如图10所示。帷幕墙体建设要求满足抵抗4 MPa大小的水压力,通过抗压强度测试,得到饱水状态下该浆液结石体的强度为11.2 MPa,因此能够满足帷幕墙建设的强度要求。综上所述,根据文中计算得到的注浆扩散范围,设计的帷幕注浆孔距20 m能够满足现场帷幕墙建造的需要。

图10 注浆层位浆液结石体
Fig.10 Grout stone body
1)针对朱仙庄煤矿“五含”帷幕墙建设的注浆问题,研究了不同水灰比下单液水泥浆的性能。单液水泥浆水灰比越大,浆液的凝结时间越长、黏度越大,而结石率与抗压强度越小,根据浆液性能参数,并按照地层类型的不同选取相应水灰比的浆液以满足现场注浆要求。
2)建立含水层中浆液扩散的数学模型,并采用COMSOL Multiphysics软件研究了浆液的扩散规律,不同工况下浆液扩散形式以注浆孔为中心的圆形扩散。浆液的扩散半径随注浆时间的增加而增大,但扩散半径最终趋于稳定,稳定后的浆液扩散半径的平均值为10.22 m,浆液扩散的范围可达到20.44 m。
3)通过理论计算得到浆液的扩散半径,并与数值模拟结果进行对比发现,相同工况下,浆液扩散半径的理论解与数值解两者的误差控制在5%以内,说明文中所建立的数值模型研究含水层中浆液的扩散规律具有一定可靠性,计算结果能够为现场注浆工程提供数据参考。
4)根据数值模拟计算与理论分析得到的浆液扩散半径,帷幕墙建设中注浆孔距布设为20 m,两排交错布孔,建立有效宽度约为40 m的帷幕墙,以阻隔来自帷幕墙外侧“五含”及奥灰水对矿井的补给。帷幕墙建造完成后,通过检查孔对受注地层进行取心,得到了含有浆液结石体的岩心,且保水状态下该浆液结石体的岩心强度为11.2 MPa,能够满足帷幕墙建设的强度要求,证实文中注浆孔间距设计的合理性。
[1] 虎维岳.矿山水害防治理论与方法[M].北京:煤炭工业出版社,2005.
[2] 虎维岳,吕汉江.饱水岩溶裂隙岩体注浆改造关键参数的确定方法[J].煤炭学报,2012,37(4):596-601.
HU Weiyue,LYU Hanjiang.Determination method of key parameters of grouting in water saturated karst-fracture [J].Journal of China Coal Society,2012,37(4):596-601.
[3] 尹尚先,徐 维,尹慧超,等.深部开采底板厚隔水层突水危险性评价方法研究[J].煤炭科学技术,2020,48(1):83-89.
YIN Shangxian,XU Wei,YIN Huichao,et al.Study on risk assessment method of water inrush from thick floor aquifuge in deep mining[J].Coal Science and Technology,2020,48(1):83-89.
[4] 王 凯.全风化花岗岩富水地层注浆加固机理及应用[D].济南:山东大学,2017.
[5] 杨秀竹,王星华,雷金山.宾汉体浆液扩散半径的研究及应用[J].水利学报,2004(6):75-79.
YANG Xiuzhu,WANG Xinghua,LEI Jinshan.Study on grouting diffusion radius of Bingham fluids[J].Journal of Hydraulic Engineering,2004(6):75-79.
[6] 杨秀竹,雷金山,夏力农,等.幂律型浆液扩散半径研究[J].岩土力学,2005,26(11):112-115.
YANG Xiuzhu,LEI Jinshan,XIA Linong,et al.Study on grouting diffusion radius of exponential fluids[J].Rock and Soil Mechanics,2005,26(11):112-115.
[7] SAADA Z,CANOU J,DORMIEUX L,et al.Evaluation of elementary filtration properties of a cement grout injected in a sand[J].Canadian Geotechnical Journal,2006,43(12):1273-1289.
[8] CHUPIN O,SAIYOURI N,HICHER P Y.The effects of filtration on the injection of cement-based grouts in sand columns[J].Transport in Porous Media,2008,72(2):227-240.
[9] 湛铠瑜,隋旺华,高 岳.单一裂隙动水注浆扩散模型[J].岩土力学,2011,32(6):1659-1663.
ZHAN Kaiyu,SUI Wanghua,GAO Yue.A model for grouting into single fracture with flowing water [J].Rock and Soil Mechanics,2011,32(6):1659-1663.
[10] 张改玲,湛铠瑜,隋旺华.水流速度对单裂隙化学注浆浆液扩散影响的试验研究[J].煤炭学报,2011,36(3):403-406.
ZHANG Gailing,ZHAN Kaiyu,SUI Wanghua.Experimental investigation of the impact of flow velocityon grout propagation during chemical grouting into a fracture with flowing water[J].Journal of China Coal Society,2011,36(3):403-406.
[11] 俞文生,李 鹏,张 霄,等.可变倾角单裂隙动水注浆模型试验研究[J].岩土力学,2014,35(8):2137-2143.
YU Wensheng,LI Peng,ZHANG Xiao,et al.Model test research on hydrodynamic groutingfor single fracture with variable inclinations[J].Rock and Soil Mechanics,2014,35(8):2137-2143.
[12] 李术才,刘人太,张庆松,等.基于黏度时变性的水泥-玻璃浆液扩散机制研究[J].岩石力学与工程学报,2013,32(12):2415-2421.
LI Shucai,LIU Rentai,ZHANG Qingsong,et al.Research on C-S slurry diffusion mechanism with time-dependent behavior of viscosity [J].Chinese Journal of Rock Mechanics and Engineering,2013,32(12):2415-2421.
[13] 李术才,孙子正,刘人太,等.基于裂隙动水注浆的水泥-水玻璃浆液相界面特征研究[J].岩石力学与工程学报,2013,32(8):1640-1646.
LI Shucai,SUN Zizheng,LIU Rentai,et al.Research on phase interface characteristics of chement-silicate grout based on crack grouting with dynamic water[J].Chinese Journal of Rock Mechanics and Engineering,2013,32(8):1640-1646.
[14] 李术才,郑 卓,刘人太,等.基于渗滤效应的多孔介质渗透注浆扩散规律分析[J].岩石力学与工程学报,2015,34(12):2401-2409.
LI Shucai,ZHENG Zhuo,LIU Rentai,et al.Analysis of diffusion of grout in porous media considering infiltration effects[J].Chinese Journal of Rock Mechanics and Engineering,2015,34(12):2401-2409.
[15] 张庆松,王洪波,刘人太,等.考虑浆液扩散路径的多孔介质渗透注浆机理研究[J].岩土工程学报,2018,40(5):918-924.
ZHANG Qingsong,WANG Hongbo,LIU Rentai,et al.Infiltration grouting mechanism of porous media considering diffusion paths of grout[J].Chinese Journal of Geotechnical Engineering,2018,40(5):918-924.
[16] 张庆松,张连震,张 霄,等.基于浆液黏度时空变化的水平裂隙岩体注浆扩散机制[J].岩石力学与工程学报,2015,34(6):1198-1210.
ZHANG Qingsong,ZHANG Lianzhen,ZHANG Xiao,et al.Grouting diffusion in a horizontal crack considering temporal and spatial variation of viscosity[J].Chinese Journal of Rock Mechanics and Engineering,2015,34(6):1198-1210.
[17] 张庆松,张连震,刘人太,等.水泥-水玻璃浆液裂隙注浆扩散的室内试验研究[J].岩土力学,2015,36(8):2159-2168.
ZHANG Qingsong,ZHANG Lianzhen,LIU Rentai,et al.Laboratory experimental study of cement-silicate slurry diffusion law of crack grouting with dynamic water[J].Rock and Soil Mechanics,2015,36(8):2159-2168.
[18] 刘泉声,卢超波,刘 滨,等.深部巷道注浆加固浆液扩散机理与应用研究[J].采矿与安全工程学报,2014,31(3):333-339.
LIU Quansheng,LU Chaobo,LIU Bin,et al.Research on the grouting diffusion mechanism and its application of grouting reinforcement in deep roadway[J].Journal of Mining &Safety Engineering,2014,31(3):333-339.
[19] 黄耀光,王连国,陆银龙.巷道围岩全断面锚注浆液渗透扩散规律研究[J].采矿与安全工程学报,2015,32(2):240-246.
HUANG Yaoguang,WANG Lianguo,LIU Yinlong.Study on the law of slurry diffusion within roadway surrounding rock during the whole section bolt-grouting process [J].Journal of Mining &Safety Engineering,2015,32(2):240-246.
[20] 刘 健,刘人太,张 霄,等.水泥浆液裂隙注浆扩散规律模型试验与数值模拟[J].岩石力学与工程学报,2012,31(12):2445-2452.
LIU Jian,LIU Rentai,ZHANG Xiao,et al.Diffusion law model test and numerical simulation of cement fracture groution [J].Chinese Journal of Rock Mechanics and Engineering,2012,31(12):2445-2452.
[21] 邓韶辉,王晓玲,敖雪菲,等.大坝基岩帷幕宾汉姆浆液灌浆的三维数值模拟[J].水利学报,2016,47(2):165-172.
DENG Shaohui,WANG Xiaoling,AO Xuefei,et al.Three-dimensional numerical simulation of curtain grouting in the dam bedrock based on binghamian grouts[J].Journal of Hydraulic Engineering,2016,47(2):165-172.
[22] 孔祥言.高等渗流力学[M].合肥:中国科学技术大学出版社,2010.
[23] 刘人太.水泥基速凝浆液地下工程动水注浆扩散封堵机理及应用研究[D].济南:山东大学,2012.