
移动扫码阅读
20世纪60年代法国工程师HENRI VIDAL[1]提出现代加筋土理论并成功在法国修建世界上第一座加筋土挡墙后,该技术引起了世界各国工程界、学术界的重视,其发展速度相当快,应用范围也日益广泛。1988年之后,我国各行业相继出版了土工合成材料应用的相关技术标准、规范和指南,对主要加筋土结构的设计应用等进行了规定和说明,对我国土工合成材料加筋土结构的应用起到了积极的推动作用。加筋土挡墙作为一种柔性支挡结构[2-3],具有经济、节省场地面积、地基承载力要求低、抗震性能好等优点。一直以来加筋土挡墙的应用与研究以道路边坡为主,近年随着场地边坡应用的增多,一些学者开始了对筋土挡墙场地边坡应用的研究。PORTELINHA等[4]、YAZDANDOUST[5]、ALRKABY等[6]开展了一系列现场以及模型试验,对加筋土挡墙的性状进行了研究。刘晓明等[7]通过某红砂岩地区加筋土挡墙凸形拐角段发生的面板鼓胀现象及变形量测结果,分析了凸角区鼓胀变形的原因。KI等[8]通过一系列模型试验分析了加筋土挡墙的拐角段在不同弯曲截面下的水平位移。ZHANG等[9-11]基于极限平衡理论,分析了不同几何参数和材料属性下,拐角对三维斜坡稳定性的影响;后利用变分原理导出的3D机制分析了斜坡凸形拐角的三维稳定性;随后,基于三维斜坡拐角的内部稳定性分析,开发了计算其所需强度和加固长度的分析程序。
然而国内外关于加筋土挡墙拐角形式对拐角处变形特征影响的研究是有限的。为进一步掌握加筋土挡墙凸形拐角段的变形特性,笔者利用FLAC3D软件,对一座高11.9 m的红砂岩填土加筋土挡墙进行了数值模拟,分析了工程中常见的折角、圆角、直角3种拐角形式,并对鼓胀现象的成因进行了分析,将数值计算与现场鼓胀变形测量结果进行比较分析,对加筋土挡墙在拐角段的设计提出合理化建议。
红砂岩地区某场地内外高差7.00~16.00 m,其中K1+370~K1+730段因地表人工填土较厚且地基承载力不足,遂选用加筋土挡墙结构,其剖面结构如图1所示。图2为挡土墙拐角段平面示意图,其转角为90°,长度6 m。该加筋土挡墙的面板采用厚度0.25 m的C25预制混凝土面板;筋带采用CAT30020B型钢塑复合拉筋带,水平和竖向间距均为0.5 m;填料采用当地红砂岩,规定距面板0.8 m范围内填料压实度不小于90%,其余范围内压实度不小于95%。

图1 加筋土挡墙结构
Fig.1 Structure of reinforcement retaining wall

图2 拐角段平面示意
Fig.2 Plan of corner section
2003年7月竣工后,逐渐发现挡墙有地表下沉、墙面鼓胀现象,鼓胀外观如图3所示。为解决该问题,2005年建设方对墙内紧邻挡土墙的地表进行了硬化,虽然此后下沉和膨胀速率有一定的缓解,但并没有完全阻止病害的发展。到2010年,加筋土挡墙面板的鼓胀变形已经明显可见,同时发现面板顶部的围墙基础也向墙外倾斜。

图3 加筋土挡墙鼓胀外观[7]
Fig.3 Bulging appearance of reinforced earth retaining wall[7]
对比加筋土挡墙在直线段与拐角段结构上的差异,分析认为拐角段的鼓胀病害是由2个方面原因造成的:①因为拐角段属于稳定性不良地形,从直线段的二维平面应变过渡到拐角段的三维应变后,拐角段墙面的水平应力会显著增大进而导致挡墙发生鼓胀变形。图4为直线部位和拐角部位的受力分析图。对于直线部位,在自重条件下,挡墙对墙面的主动土压力为Ea;对于拐角部位,在自重条件下,左侧、右侧墙面均受到来自挡墙的大小为Ea的主动土压力,在挡墙拐角部位的合力就为![]() 因此,拐角部位所产生主动土压力较直线部位明显增大是拐角部位变形较大的重要原因。②因为在工程实践中,筋带在拐角段的重叠不可避免,使筋带的抗拉强度变小从而导致挡墙发生鼓胀变形。笔者通过数值分析方法建立具有不同拐角形式的加筋土挡墙,分析研究其变形特征。
因此,拐角部位所产生主动土压力较直线部位明显增大是拐角部位变形较大的重要原因。②因为在工程实践中,筋带在拐角段的重叠不可避免,使筋带的抗拉强度变小从而导致挡墙发生鼓胀变形。笔者通过数值分析方法建立具有不同拐角形式的加筋土挡墙,分析研究其变形特征。

图4 加筋土挡墙受力分析
Fig.4 Stress analysis of reinforced earth retaining wall
通过FLAC3D有限差分软件,按与原型加筋土挡墙1∶1的比例建立几何模型,其几何模型如图5所示。模型沿X、Y轴方向截取的长度均为20 m,挡墙高度11.9 m,底部地基为1.5 m。凸形拐角处转角为90°,分别以边长(半径)4.24 m,建立工程上常采用的折角、圆角、直角3种拐角形式(以下简称折角、圆角、直角)的加筋土挡墙。在模型底部固定其x、y和z轴方向的速度,面x=0固定其x轴方向的速度,面y=0固定其y轴方向的速度。

图5 加筋土挡墙几何模型
Fig.5 Geometric model of reinforced retaining wall
通过zone单元建立地基、墙后填土的网格模型。采用FLAC3D系统自带的Geogrid单元模拟加筋结构,土工格栅长度为10 m,竖向间距0.5 m,共24层。面板采用Liner单元进行模拟,图6为结构单元几何模型。

图6 结构单元几何模型
Fig.6 Geometric model of structural elements
地基和挡墙均采用Mohr-Coulomb本构模型,挡土墙原型取当地红砂岩为填料,面板为0.25 m厚的C25预制混凝土面板,根据相关资料[12-14]列出的参数取值范围,进行了模型的参数取值。
详细数值模型参数见表1—表3。软件自有的Geogrid结构单元采用CST壳有限单元,即能承受薄膜荷载而不能抵抗弯曲荷载,其可与实体单元发生直接的剪切摩擦作用,格栅法向的运动从属于实体单元。Liner结构单元能承受剪力及弯矩荷载,一方面不但能承受主方向的拉压应力,还能模拟其与土体直接的分离再接触,另一方面能模拟其与土体之间的摩擦相互作用。
表1 数值模型参数
Table 1 Material property for numerical model

项目密度/(kg·m-3)体积模量/MPa剪切模量/MPa黏聚力/kPa内摩擦角/(°)填土190042195631地基240014100120012000000
表2 Geogrid单元数值模型参数
Table 2 Geogrid numerical model parameters
弹性模量/MPa泊松比厚度/mm耦合弹簧单位面积刚度/kPa耦合弹簧黏聚力/kPa耦合弹簧内摩擦角/(°)260000.3352500230
表3 Liner单元数值模型参数
Table 3 Liner numerical model parameters
弹性模量/MPa泊松比厚度/mm法向耦合弹簧积刚度/(MPa·m-1)切向耦合弹簧积刚度/(MPa·m-1)280000.20250898898
2.2.1 整体变形
图7为3种拐角形式(折角、圆角、直角)的整体变形云图,观察发现集中变形区在挡墙的上部,且在拐角部位的变形明显大于两侧直线段的变形。其中,圆角的最大变形达到了26.7 mm,直角最大变形为27.3 mm,折角最大变形为25.1 mm。

图7 整体变形
Fig.7 Contour of global deformation
2.2.2 竖向变形
图8分别为3种拐角形式的竖向变形和切片云图,切片的位置为拐角的角平分线。圆角的竖向变形达到了26.2 cm,直角为26.8 cm,折角为24.6 cm。竖向变形的集中变形区位置与整体变形的集中变形区位置一样,都在挡墙的上部。对比竖向变形与整体变形,竖向变形不仅在变形量上与整体变形非常相近,而且他们的集中变形区域位置也相同,说明竖向变形对整体变形的发展影响很大。

图8 竖向变形及切片
Fig.8 Contour of vertical deformation and cutting planes
图9为挡墙拐角段墙顶角平分线上的竖向变形,挡墙顶面的竖向变形呈“L”形,分析认为是由于面板与土工格栅的链接作用,使得面板附近的土体在竖向变形上受到了限制。该限制力随着土体与面板距离的增加逐渐减弱,竖向变形开始显著增大。可以看到,圆角的竖向变形在远离面板方向发展速度最快,最先于距面板2.9 m的位置达到竖向最大变形,折角次之,于4.8 m位置达到竖向最大变形,直角发展最慢,于6.2 m位置达到竖向最大变形。
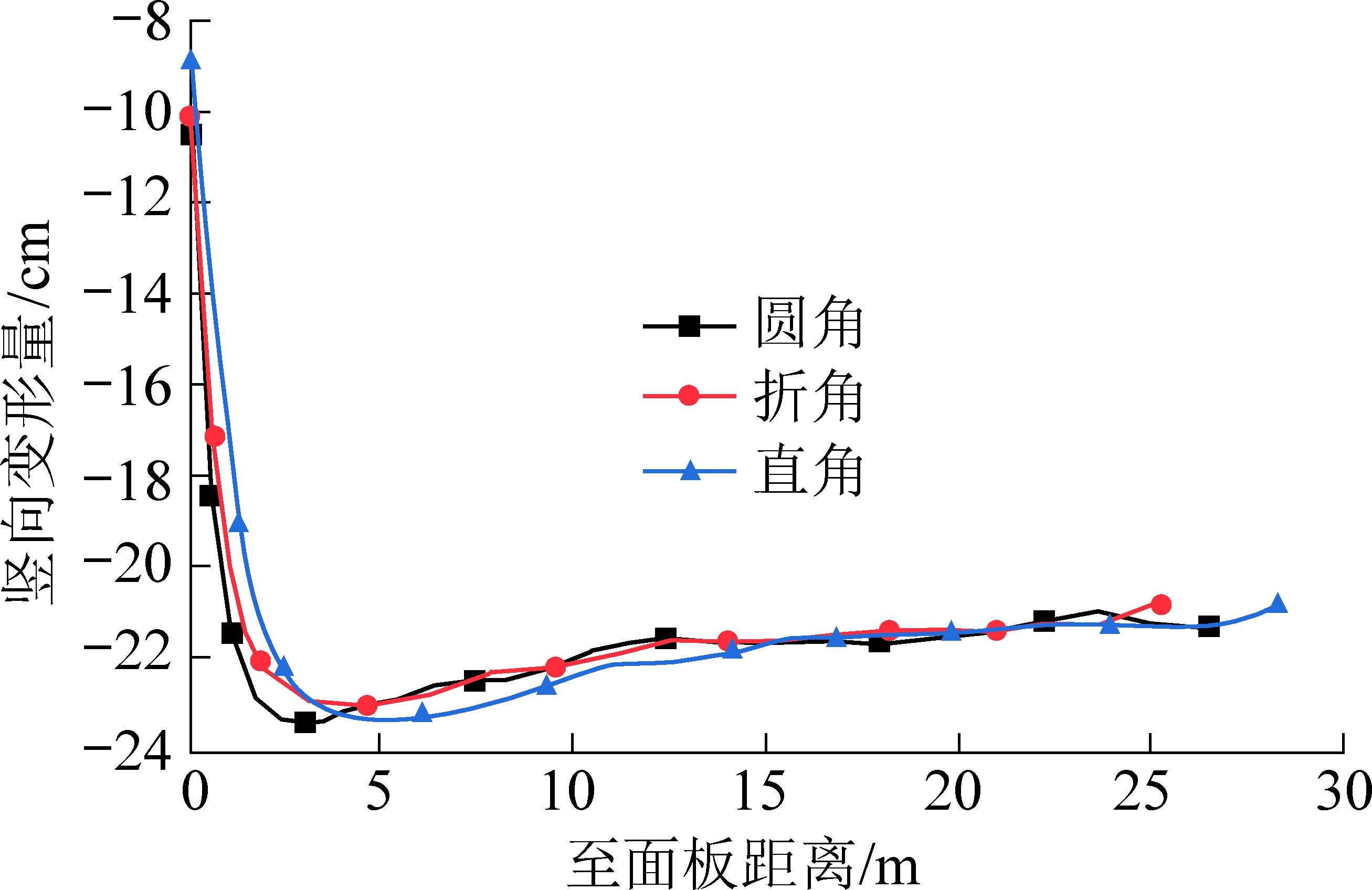
图9 竖向变形
Fig.9 Vertical deformation
2.2.3 水平变形
图10分别为3种拐角形式的水平变形和切片云图,对比拐角段和两侧直线段,3种形式在其拐角段的1/4~2/3区域都呈现鼓胀变形[15],另外,在拐角段的顶部,3种形式的面板都有一定程度的外倾[16],这与现场发现的面板顶部的围墙基础向墙外倾斜的情况相吻合。折角的最大水平变形为7.49 cm,圆角的最大水平变形为7.66 cm,直角的最大水平变形为7.75 cm。
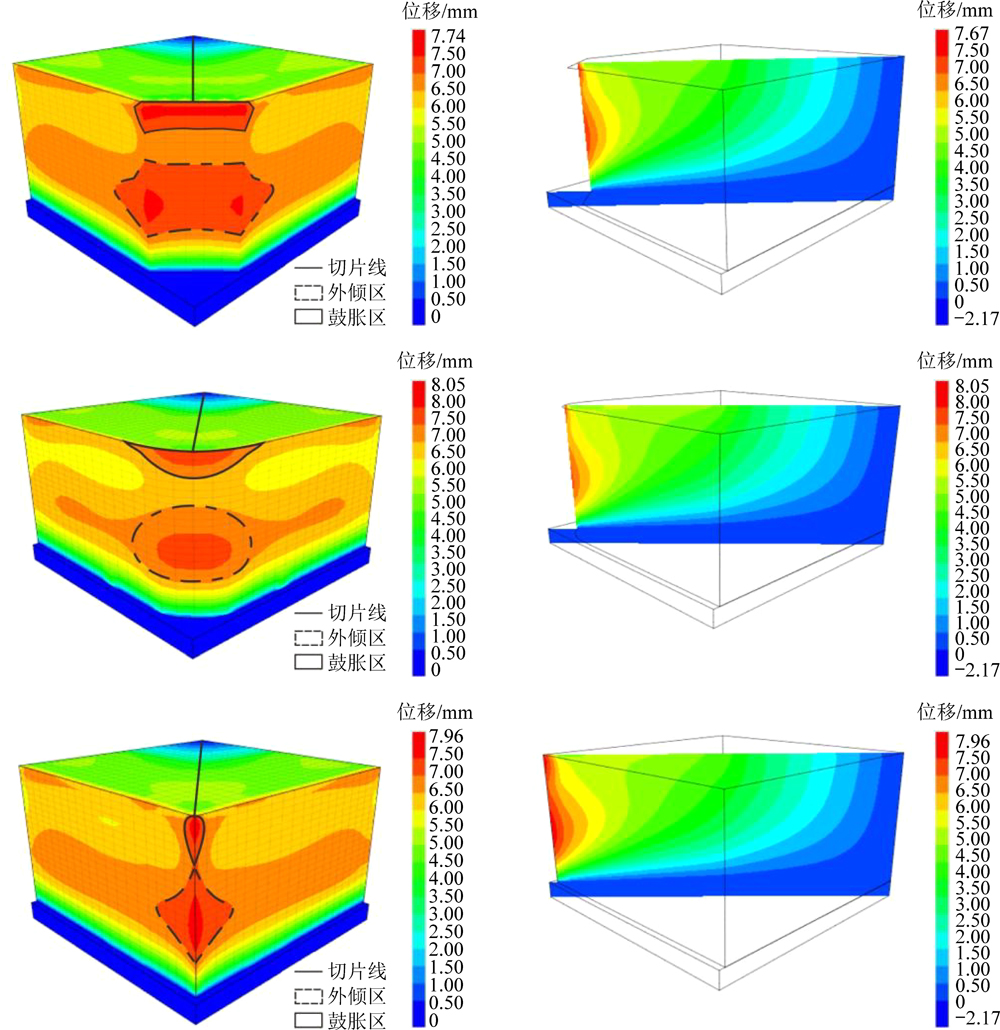
图10 水平变形及切片云图
Fig.10 Contour of horizontal deformation and cutting planes
图11为拐角段切片上面板沿墙高的水平变形。3种形式挡墙水平变形规律相同,在5 m墙高的位置达到最大鼓胀变形,在面板顶部的位置达到最大外倾变形。
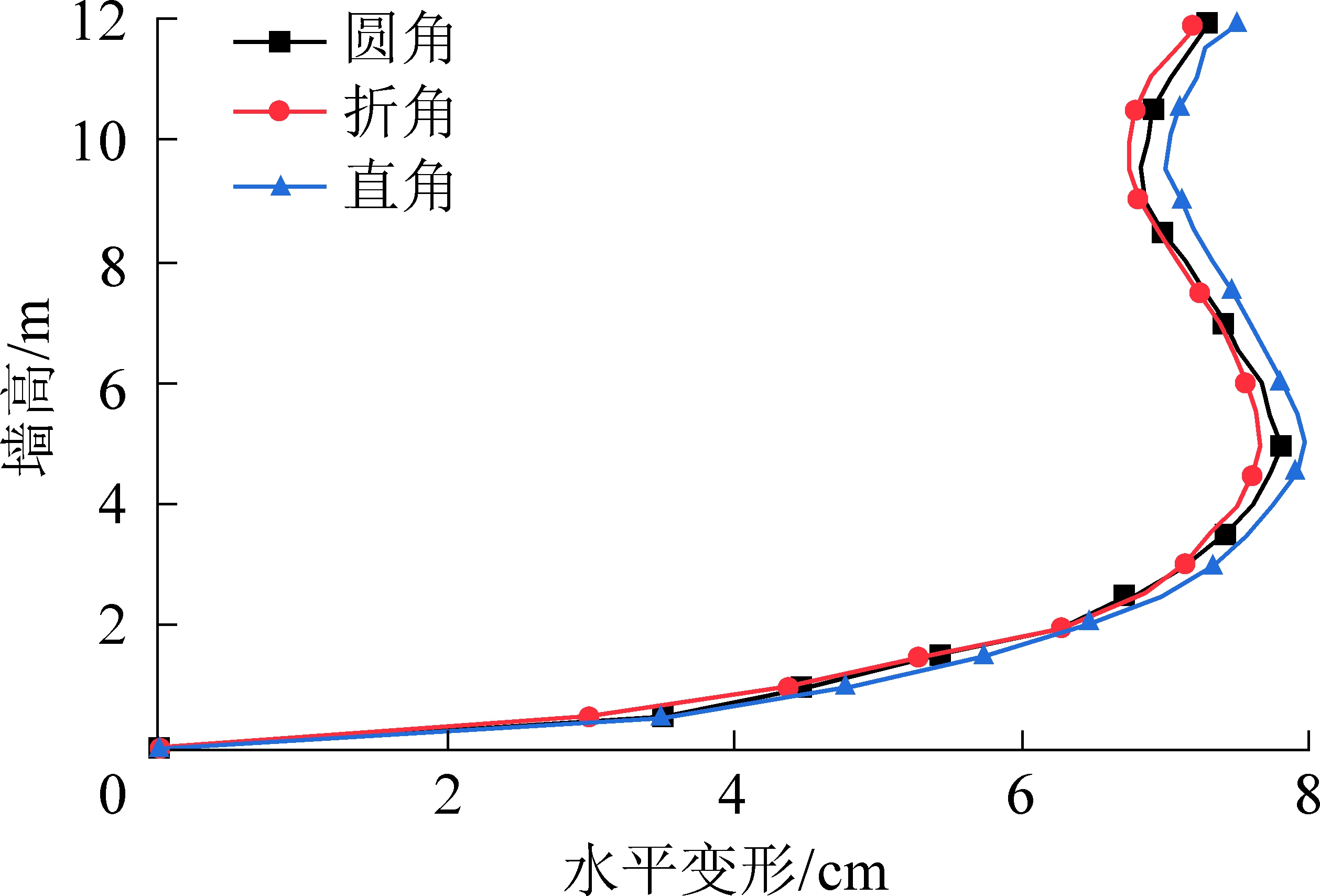
图11 水平变形
Fig.11 Horizontal deformation
2.2.4 鼓胀区域
图12为5 m高处面板的水平变形,可以看到从两侧直线段过渡到拐角段对称中心的时候,水平变形逐渐增大,其中折角在两个转折的地方有相同的峰值,圆角和直角都只在中心线上有峰值。对比3条曲线发现,从过渡段开始直角的水平变形一直小于另外2种形式,但是在接近中心线时,直角的水平变形迅速增大并超过了另外2种形式。这说明直角不利于应力扩散,使应力应变更加集中在拐角中心线附近,参与协调变形的区域更小,图9中的鼓胀区大小直观地体现了这一特征,直角的鼓胀区域面积明显小于其他2种形式,这是直角的水平变形大于另外2种形式的原因。折角分别在2个转折的地方有相同的峰值,可以认为折角是2个“直角”的结合,在2个转折的地方,水平变形迅速增大并达到峰值。折角的鼓胀区面积最大,分析认为是2个折角为应力应变扩散提供了良好的条件,这使得其最大变形小于圆角。
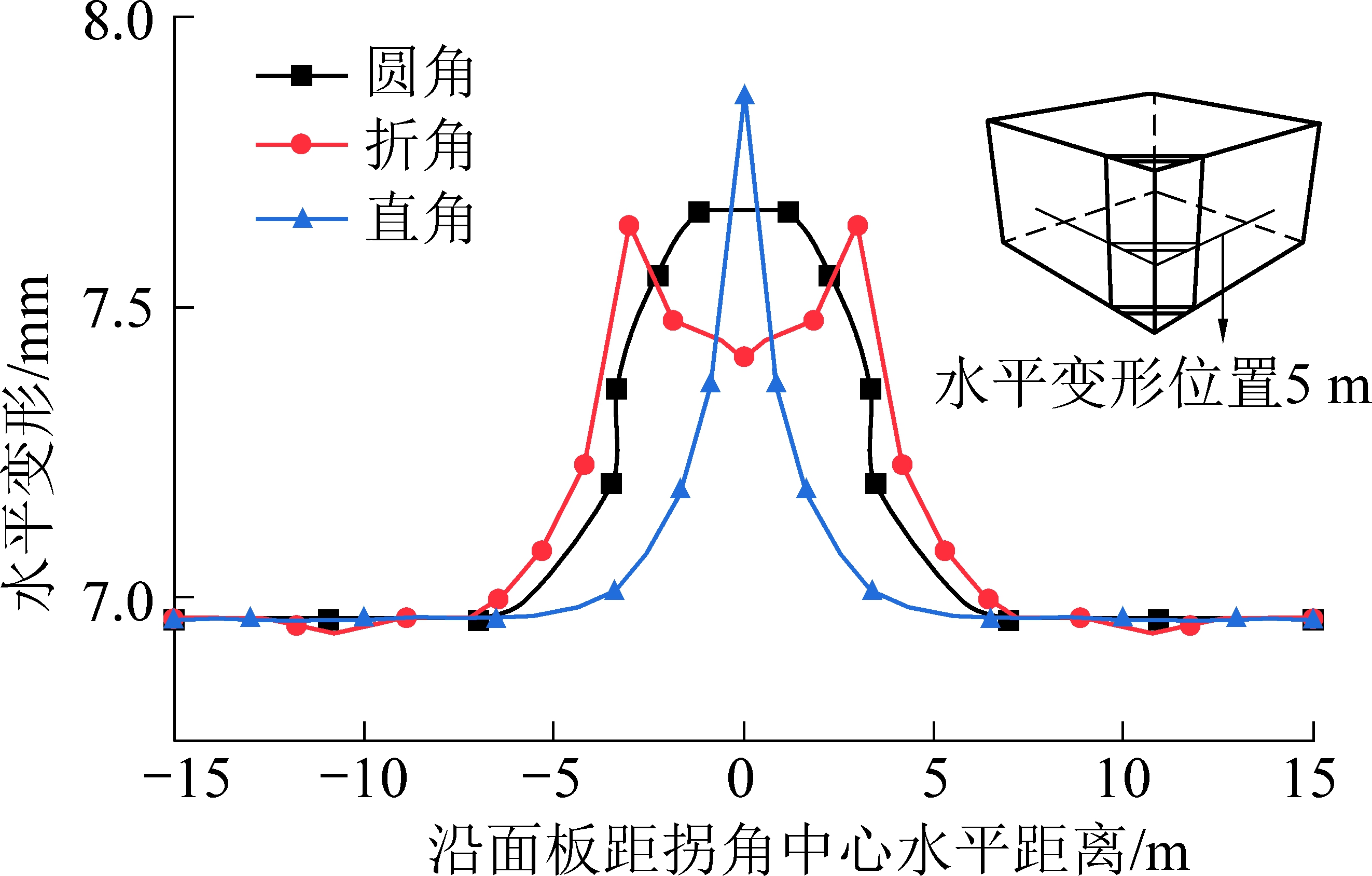
图12 5 m高处水平变形
Fig.12 Horizontal deformation at height of 5 m
加筋土挡墙凸形拐角段鼓胀最为显著,经测量,距离墙顶3 m处的墙身鼓胀量约9 cm,两侧由拐角段向直线段过渡的过渡段也各有4 m范围对称鼓胀,凸角两侧4 m以外段落的鼓胀已经不明显。即挡墙变形有以下特征:①面板中部有鼓胀变形,且鼓胀区域向两侧直线段延伸4 m;②面板顶部的围墙基础向墙外倾斜;③挡墙顶部地表在面板附近下沉严重。图13为水平变形的模拟结果与测量数据,图14为挡墙的变形特征,说明用数值模型计算加筋土挡墙凸形拐角部位的变形特征是可行的。
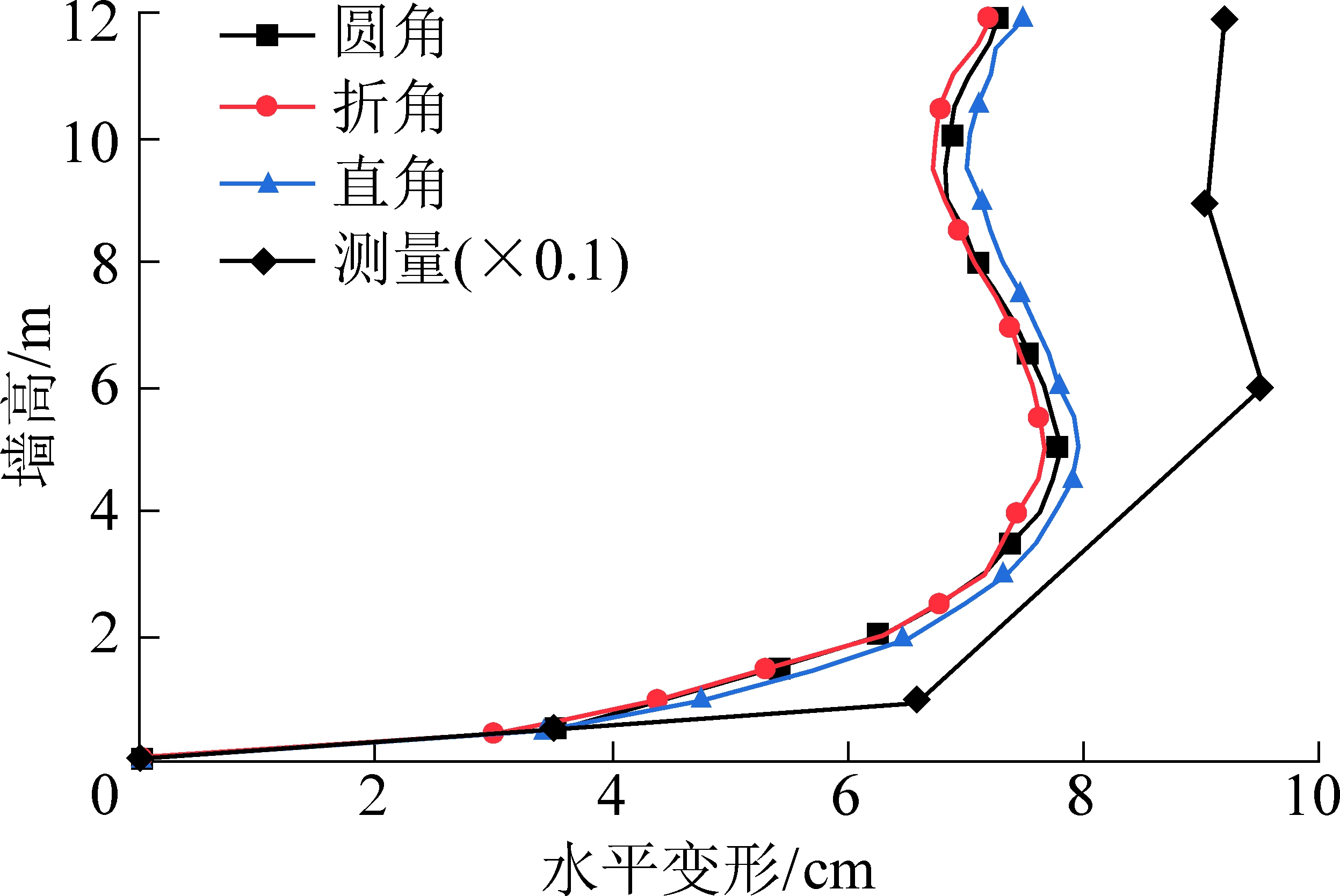
图13 水平变形
Fig.13 Horizontal deformation
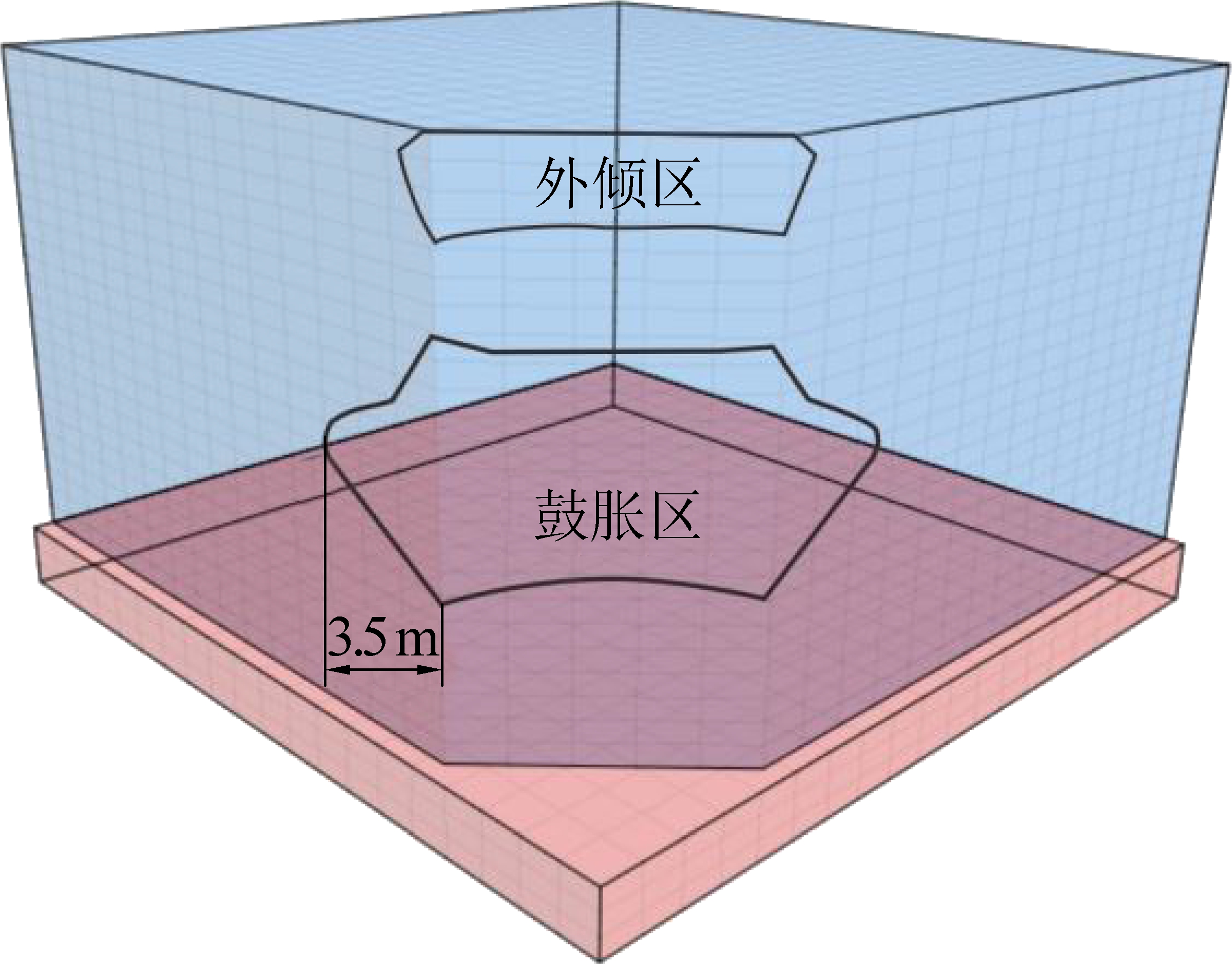
图14 变形特征
Fig.14 Deformation feature
1)数值模型计算结果与现场测量结果吻合较好。加筋土挡墙的变形集中在挡墙上部,其中竖向变形对整体变形的发展影响很大。3种拐角形式的最大竖向变形位置离面板的距离不同,圆角距离最近,折角居中,直角距离最远。
2)在拐角段墙高的1/4~2/3段为鼓胀区,墙顶为外倾区。
3)在整体变形以及水平变形方面,尤其是在对面板形态有重要影响的水平变形上,因折角形式的结构特征使得其在应力应变的扩散上更具优势,从而具有3种形式中最小的最大变形值,即折角在控制变形方面较其他2种形式有更好的优势,建议在工程设计中应优先使用。
[1] VIDAL H.The principle of reinforced earth[J].Transportation Research Record,1969,282:1-16.
[2] JIE Han,LESHCHINSKY D.General analytical framework for design of flexible reinforced earth structures[J].Journal of Geotechnical and Geoenvironmental Engineering,2006,132(11):1427-1435.
[3] SONG F,XIE Y L,YANG Y F,et al.Analysis of failure of flexible geocell-reinforced retaining walls in the centrifuge[J].Geosynthetics International,2014,21(6):342-351.
[4] PORTELINHA F H M,ZORNBERG J G.Effect of infiltration on the performance of an unsaturated geotextile-reinforced soil wall[J].Geotextiles and Geomembranes,2017,45(3):211-226.
[5] YAZDANDOUST M.Laboratory evaluation of dynamic behavior of steel-strip mechanically stabilized earth walls[J].Soils and Foundations,2018,58(2):264-276.
[6] ALRKABY A,CHEGENIZADEH A,NIKRAZ H.Anisotropic strength of large scale geogrid-reinforced sand:experimental study[J].Soils and Foundations,2016,57(4):557-574.
[7] 刘晓明,袁振宇,陈昌富,等.红砂岩地区某加筋土挡土墙凸形拐角鼓胀病害分析[J].土木工程学报,2011,20(3):18-22.
LIU Xiaoming,YUAN Zhenyu,CHEN Changfu,et al.Analysis of convex corner bulging deterioration of reinforced earth retaining wall in red sandstone area[J].China Civil Engineering Journal,2011,20(3):18-22.
[8] Ki,Jung Su,Rew,et al.A behavior of curve section of reinforced retaining wall by model test[J].Journal of the Korean Society of Civil Engineers,2012,32(6):249-257.
[9] ZHANG F,GAO Y,LESHCHINSKY D,et al.3D effects of turning corner on stability of geosynthetic-reinforced soil structures[J].Geotextiles and Geomembranes,2018,46(4):367-376.
[10] ZHANG F,LESHCHINSKY D,GAO Y,et al.Three-dimensional slope stability analysis of convex turning corners[J].Journal of Geotechnical and Environmental Engineering,2018,144(6):6018003.
[11] ZHANG F,Leshchinsky D,GAO Y,et al.Corner reinforced slopes:Required strength and length of reinforcement based on internal stability[J].Geotextiles and Geomembranes,2019,47(3):408-416.
[12] 黄向京,刘 泽,王 维,等.红砂岩填料与土工合成材料的筋土界面特性实验研究[J].公路工程,2009,34(4):16-19.
HUANG Xiangjin,LIU Ze,WANG Wei,et al.The experimental study on the interface characteristic between red sandstone and geosynthetics[J].Highway Engineering,2009,34(4):16-19.
[13] 陈建峰,柳军修,石振明.软弱地基刚/柔性组合墙面加筋土挡墙数值模拟[J].岩石力学与工程学报,2016,35(2):422-432.
CHEN Jianfeng,LIU Junxiu,SHI Zhenming.Numerical simulation of reinforced soil walls with flexible/rigid facings on yielding foundation[J].Chinese Journal of Rock Mechanics and Engineering,2016,35(2):422-432.
[14] 孙书伟,林 杭,任连伟.FLAC3D在岩土工程中的应用[M] .北京:中国水利水电出版社,2011.
[15] XIAO C,HAN J,ZHANG Z.Experimental study on performance of geosynthetic-reinforced soil model walls on rigid foundations subjected to static footing loading[J].Geotextiles &Geomembranes,2016,44(1):81-94.
[16] BALAKRISHNAN S,VISWANADHAM B V S.Performance evaluation of geogrid reinforced soil walls with marginal backfills through centrifuge model tests[J].Geotextiles &Geomembranes,2016,44(1):95-10.