
移动扫码阅读
采矿科学与工程

移动扫码阅读
青海省木里煤田位于祁连山南麓腹地,黄河重要支流大通河源头,是祁连山区域水源涵养地和我国生态安全屏障的重要组成部分,具有极为重要的生态地位。经过多年煤炭开采后形成的露天采坑、渣山和工业场地导致木里矿区的水、土地和植被资源均遭到了不同程度的破坏,由此引发了严重的生态环境问题。2020年,木里煤田启动了大规模的生态环境恢复治理工作。江仓矿区位于木里煤田的东部,江仓一号矿自20世纪70年代初开始进行煤炭开采,浅部采用露天开采,深部进行井工开采。在对江仓一号矿露天采坑进行回填治理的过程中,发现了采坑回填可能会对采坑下方浅埋深井工巷道稳定性产生影响的问题。虽然目前井工矿已停工,但井工矿中仍有大量的设备,井工巷道的稳定性直接关系到井工矿人员及设备出入的安全,保证井工巷道的稳定性十分重要。井工巷道受露天采坑回填影响问题的实质是回填体产生的附加应力对原已处于应力平衡状态巷道的2次扰动。相关学者对地面建/构筑物产生的附加应力及其对地下空间包括采空区及巷道的影响进行了研究[1-6]。露天采坑回填时采用各种车辆进行回填体运输、卸载、推覆等工艺也会对浅埋巷道产生扰动影响,有些学者对施工方式与施工车辆载荷对地基、地下管道、浅埋隧道等的影响进行了研究[7-15]。井工巷道具有一定自承载能力,一些学者对巷道围岩破坏、冒落拱和平衡拱高度、外来扰动和巷道稳定性进行了研究[16-20]。目前专门针对露天采坑回填对其下浅埋井工巷道稳定性影响的研究较少,露天采坑回填除了带来回填体的静载和施工车辆及其动载对井工巷道的影响,回填后采坑由于地势原因积水,水体载荷和地表水与井下间的水力联系对巷道稳定性的影响也不容忽视。
笔者通过对露天采坑回填时不同载荷形成附加应力的计算,根据附加应力影响深度和巷道极限承载高度的关系对露天采坑下井工巷道稳定性进行分析,得到巷道处于不稳定状态的条件和范围,并给出保证巷道稳定的技术措施。
江仓一号矿海拔高度+3 670~+3 815 m,属于高寒高海拔地区,目前地面已形成了最大深度约120 m,坑口面积约70.2万 m3,容积约2 727万 m3的露天采坑,采坑下方是井工矿一区段的准备巷道系统。井工矿开拓方式为斜井多水平片盘开拓,设主、副、风3条井筒,井下一水平标高为+3 450 m。井下巷道与采坑回填体位置关系平面如图1所示,沿一区段回风石门做倾向剖面Ⅰ—Ⅰ和走向剖面Ⅱ—Ⅱ如图2所示。图中显示距离采坑底部最近的有3条巷道:一区段回风斜巷、+3 650运输石门和+3 650轨道石门。一区段回风斜巷距离地表采坑最近处只有27.07 m。一区段回风斜巷、+3 650运输石门和+3 650运输石门断面都为半圆拱,现有支护方式为锚网喷支护。

图1 井下巷道与采坑回填位置关系平面图
Fig.1 Plan view of underground roadways and open-pit backfilling

图2 井下巷道与采坑回填位置关系剖面图
Fig.2 Cross section view of underground roadways and open-pit backfilling
采坑回填后,将在其下方岩土体中产生附加应力。附加应力是在外载荷(回填体)作用下产生的应力增量。巷道开挖和支护后,已经达到初始平衡状态,在附加应力作用下,初始平衡状态有可能被破坏,从而导致巷道失稳。
采用法国数学家布辛奈斯克运用弹性力学推出的竖向集中力在弹性体内任一点所引起的应力解析解,对回填体产生的附加应力进行求解。如图3所示集中力作用模型,根据布辛奈斯克集中力作用下附加应力的解,可得到任意点的竖向应力的计算公式:
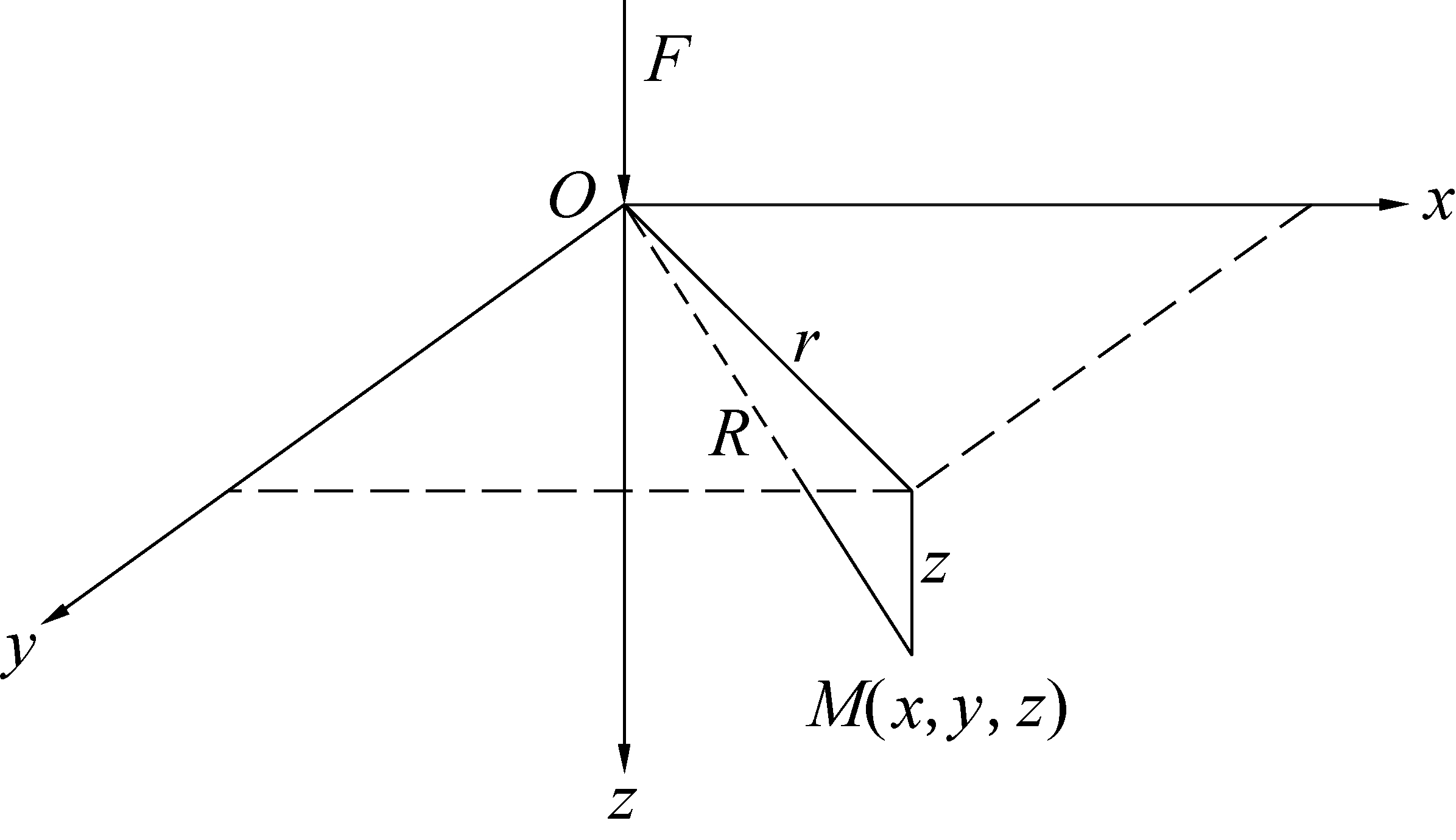
图3 集中力作用模型
Fig.3 Concentrated force model
![]()
(1)
式中,σz为M点的竖向附加应力;F为集中力;r为M点与集中力作用点的水平距离,r2=x2+y2;z为M点的竖向深度,z≥0。
矩形面积均布载荷作用下回填体附加应力计算利用式(1)进行积分求解,如图4所示,计算矩形面积均布载荷p0作用下的附加应力如式(2)所示:
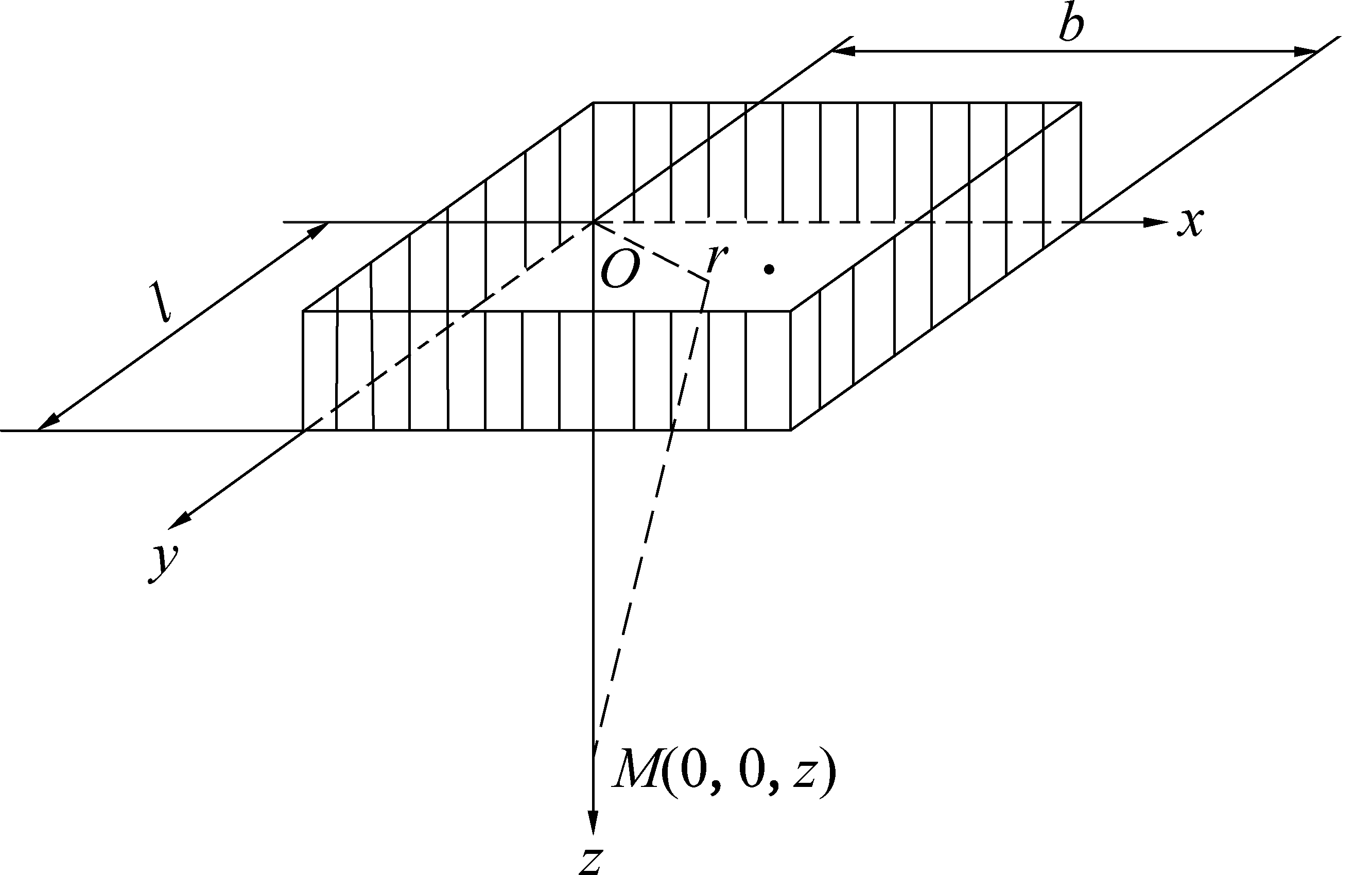
图4 矩形面积均布载荷作用下的附加应力
Fig.4 Additional stress of rectangle uniformly distributed load
![]()
![]()
(2)
式中,p0为均布载荷;l为矩形面积的长度;b为矩形面积的宽度。
考虑更一般的情况,对矩形平面下任一点M,深度为z,如图5所示,在平面上的投影为O。平面图分为Ⅰ,Ⅱ,Ⅲ,Ⅳ四个矩形。
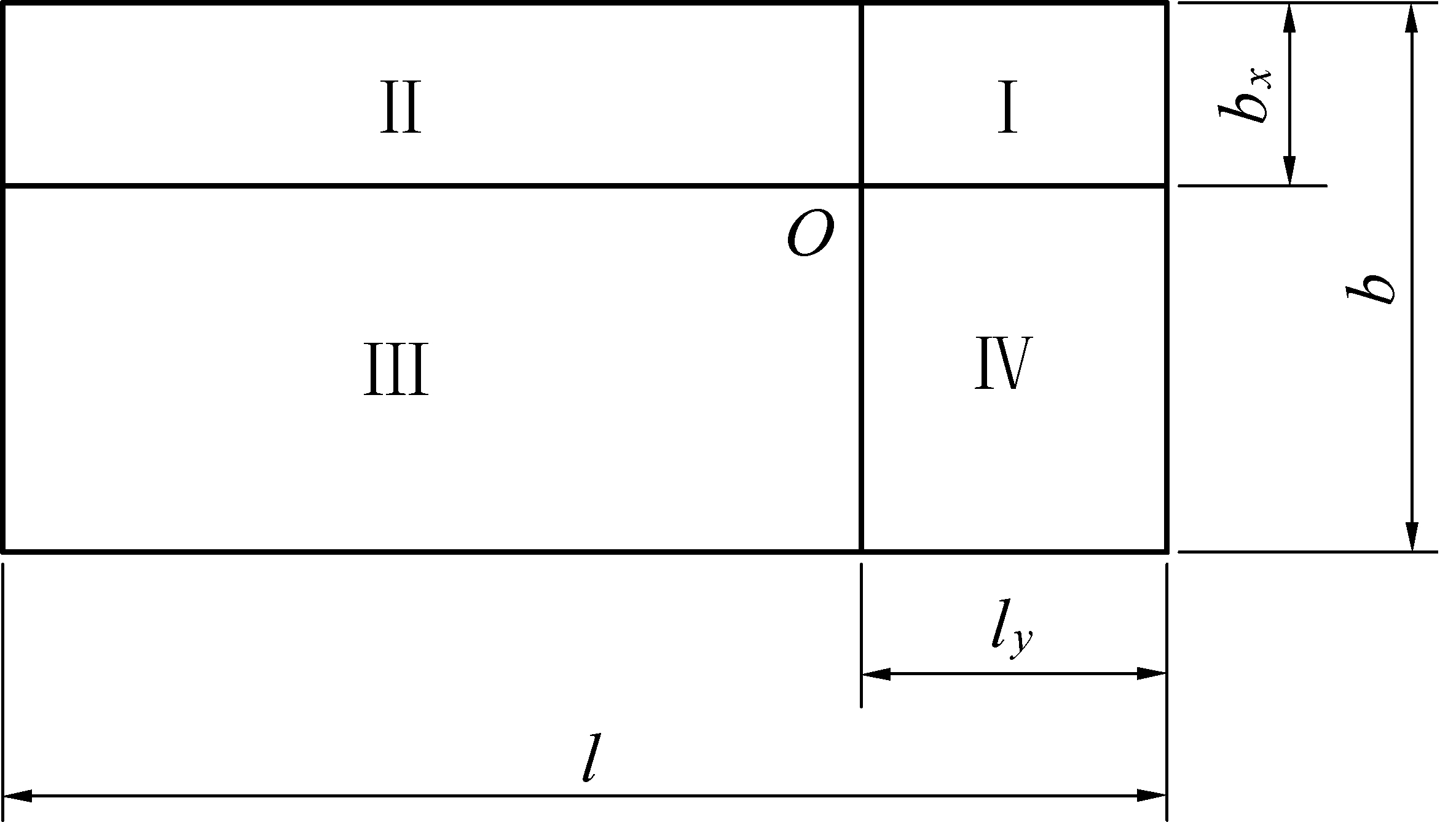
图5 矩形面积示意
Fig.5 Rectangle area sections
按式(2)可列出M点的附加应力如(3)所示。
![]()
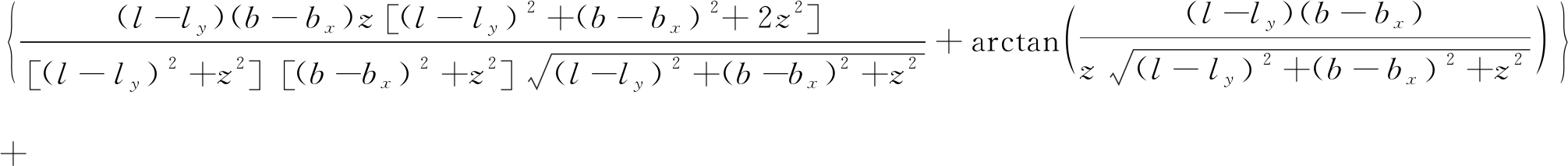
(3)
分析式(3),可得到矩形平面均布载荷下矩形平面中心点处。
即bx=1b/2,ly=1l/2位置处的竖向附加应力最大,最大附加应力为
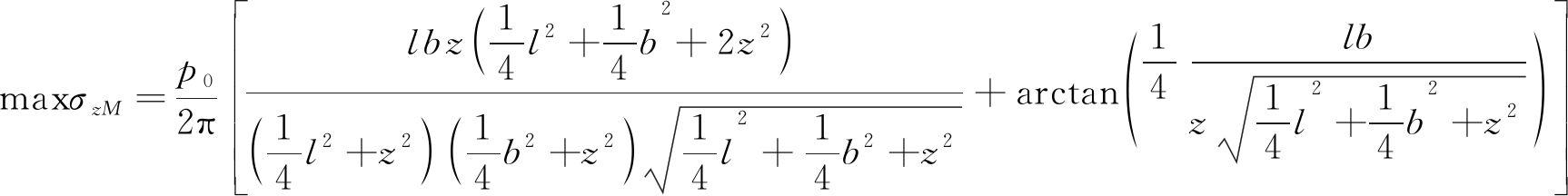
(4)
其中,
p0=γsHs
(5)
式中,γs为回填体密度,根据回填体材料类型取1 800 kg/m3;Hs为回填体高度。
车辆载荷作用在地表路面,产生的载荷来源于2部分。一部分是车辆自重产生的静态载荷,另一部分是车辆行驶过程中,轴承转动导致车轮作用路面的车辆载荷。
按《公路工程技术标准》(JTG B01—2019)中对车辆载荷的处理方法,将车辆载荷简化为移动恒载+冲击载荷。先将车辆载荷简化为静载荷(恒载),假定车辆载荷按规范规定分配到各个车轴(三轴),车轮作用在路面上的力为集中力,具体计算简图如图6所示。

图6 车辆载荷集中分布示意
Fig.6 Vehicle load distribution
如图6所示,M点总的竖向附加应力为
σzM=σz(MO)+σz(MA)+σz(MB)+σz(MC)+σz(MD)+σz(ME)
(6)
式中,σzM为车辆载荷在M点引起的竖向附加应力;σz(MO),σz(MA),σz(MB),σz(MC),σz(MD)分别为O~E处的集中载荷在M点产生的竖向附加应力,可根据式(1)分别求出。
图6中给出的是三轴载重汽车模型,x1和x2分别为车辆前中轴距和中后轴距,y0为轮距。
根据现场施工车辆型号,F=920 kN,x1=3.8 m,x2=1.5 m,y0=2.7 m。
由式(6)计算得出的是车辆载荷产生的静附加应力,按相关规范,动附加应力可由静附加应力乘一冲击系数得出:
(7)
式中,![]() 为动附加应力;μ为冲击系数,取0.1~0.4。
为动附加应力;μ为冲击系数,取0.1~0.4。
则车辆产生的最大附加应力可表示为
σzM,max=(1+μ)σzM
(8)
回填后,预计采坑内积水最终标高为+3 772 m。考虑回填体上方水体按其深度产生的自重加到巷道覆岩上,此时,
p0=γsHs+γwHw
(9)
其中,γw为水体密度,取1 000 kg/m3;Hw为水体高度。再按式(4)计算总的附加应力。
回填后采坑逐渐蓄水,采坑水可通过回填体和覆岩内的水力联系通道进入井下并可能对巷道稳定性造成一定影响。
研究区地下水类型主要可分为2类。①为第4系含水层,即多年冻土层以上的第4系及季节性冻土层,含水层为砂土砾石层、粉砂岩、细砂岩;②为基岩裂隙含水层,主要分布在多年冻土层以下,含水层以砂岩、细砂岩裂隙水为主。第4系主要为砂土砾石层,整体透水性较好。由于研究区位于多年冻土分布区,地表水排泄条件良好,大气降水或洪水期对矿床充水的影响很小。冷季时,采坑中的水以及地表以下一定范围内第4系处于冻结状态形成隔水层,无法入渗到井下;暖季时,季节性冻土融化使第4系成为完全开放的透水层,江仓河水成为采坑水的主要补给来源。江仓河水补给进入采坑的水量、水质与井工矿井排水量基本持平,说明研究区主要补给源为江仓河水,通过江仓河侵蚀融区的基岩裂隙从采坑坡面排出并通过采坑和井下巷道之间覆岩中的水力联系通道到达井下。根据井工矿实测资料,矿井涌水量为86 m3/h,矿井涌水量很小,矿井水文地质类型属简单类型,地面与井下水力联系弱。
回填后,采坑水体至巷道的距离随回填体高度而增大,采坑水必须通过回填体和覆岩内的水力联系通道才能进入井下,在气候条件和地质条件都不变的情况下,可以预测,矿井涌水量跟回填前相比不会有明显变化,地面井下的水力联系对巷道稳定性的影响没有加剧。
根据附加应力随深度变化的规律,当附加应力为该点自重应力的10%时,可认为附加应力不再对巷道产生影响,此时的深度为附加应力的影响深度Ha。如图7所示,为使巷道保持稳定,附加应力的影响深度Ha和巷道极限承载高度Hb之和应小于采坑回填前的巷道顶板埋深(覆岩厚度)H,即:H≥Ha+Hb。
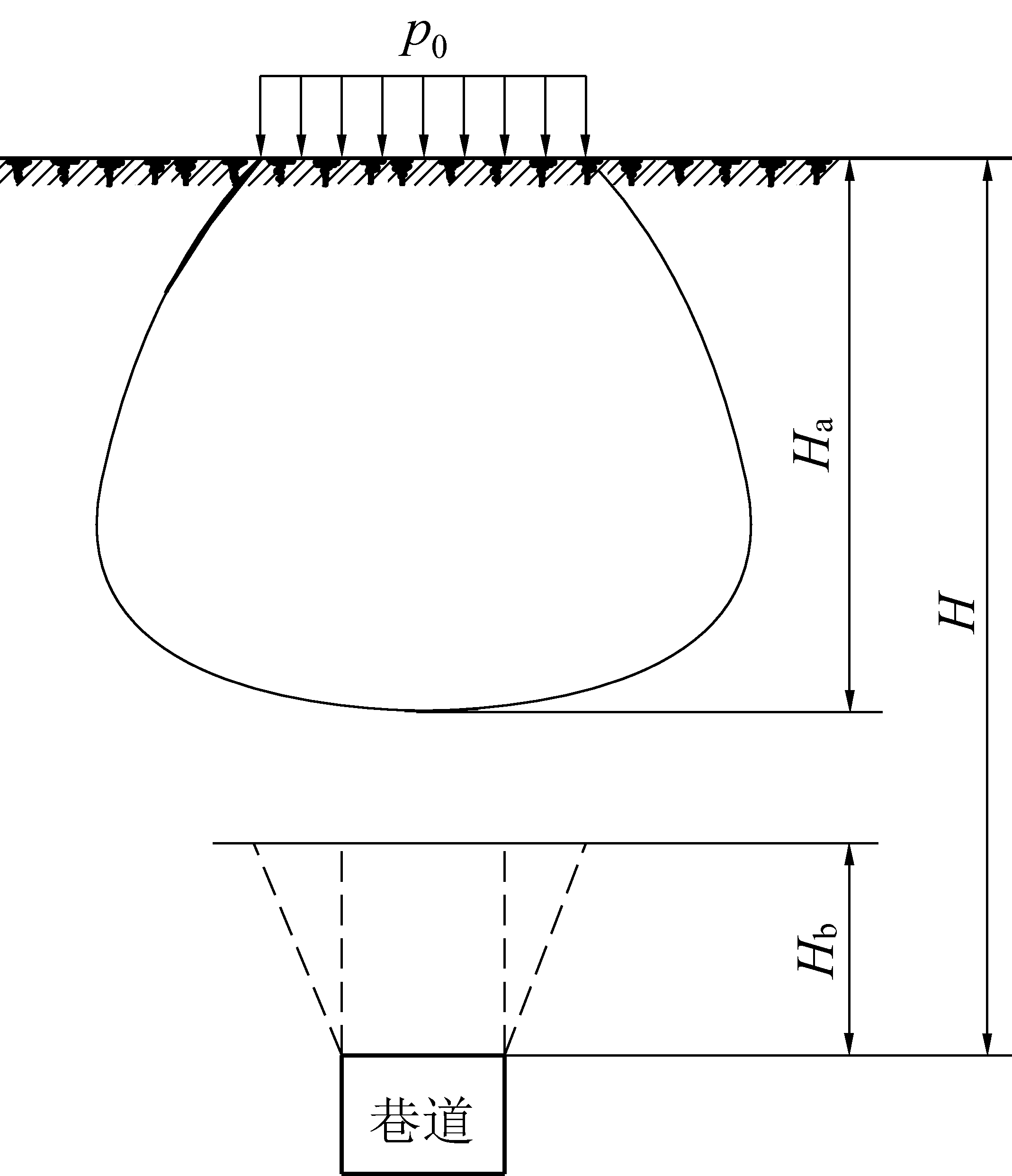
图7 附加应力影响深度及巷道极限承载高度示意
Fig.7 Influence depth of additional stress and ultimate bearing height of roadway
对于浅埋巷道极限承载高度Hb,可根据土力学极限平衡理论求出。
如图8所示,顶板岩块bcde在重力G的作用下产生沉降,两边的楔形体abc和def也对其施加水平力P。巷道实际承载力Q为
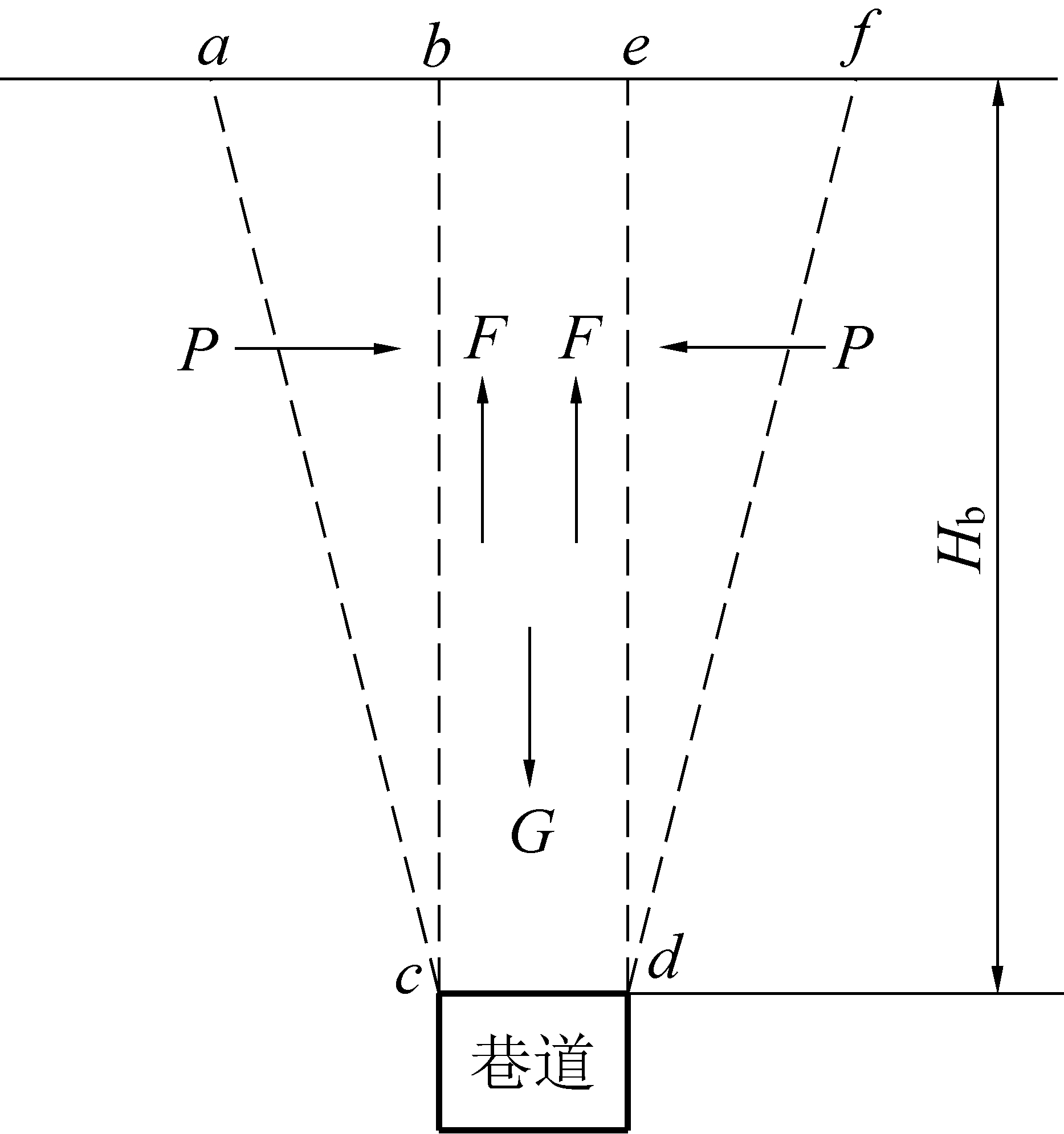
图8 巷道覆岩极限平衡示意
Fig.8 Limit equilibrium of roadway
Q=G-2Ff
(10)
当Q=0时,顶板上方岩层的重力恰好能保持自然平衡而不遭受破坏,此时Hb为巷道的极限承载高度。
G=2Ff
(11)
G=γbHb
(12)
式中,b为巷道宽度;γ为覆岩容重。
根据土力学理论,摩阻力Ff由被动土压力P乘以摩擦因数计算,被动土压力按如图8所示的三角形面积计算。
(13)
式中,Ka为被动土压力系数;φ为土体内摩擦角。
Ka=tan2(45°-φ/2)
(14)
联立式(11)—式(14),求得:
Hb=b/[(tan φ)tan2(45°-φ/2)]
(15)
一区段回风石门及斜巷的宽度b为3.3 m,+3 650运输石门、+3 650轨道石门的宽度分别为3.2,3.4 m,内摩擦角φ取30°,计算得到一区段回风石门及斜巷的极限承载高度为17.15 m,+3 650胶带石门的极限承载高度为16.63 m,+3 650轨道石门的极限承载高度为17.67 m。
将巷道(一区段回风斜巷)上方回填体简化为矩形面积载荷,考虑不利情况(巷道距离原采坑剖面线最近),如图9所示,在Ⅰ—Ⅰ剖面图上选取A、B、C、D、E、F、G、H八个点。选择依据如下:A点是一区段回风斜巷的变坡点,在A点以前,地表由坑底起坡,覆岩厚度逐渐增大。在A点以后,随着A点下方回风斜巷开始起坡,覆岩厚度逐渐减小,地表回填体的影响随之增大。在H点之后,随坑底坡度急剧增大,覆岩厚度也随之增大。如图10所示,在东西向剖面图上选取I、J、K三个点。采用式(4)和(7)计算回填体及车辆载荷产生的最大附加应力随深度变化情况。
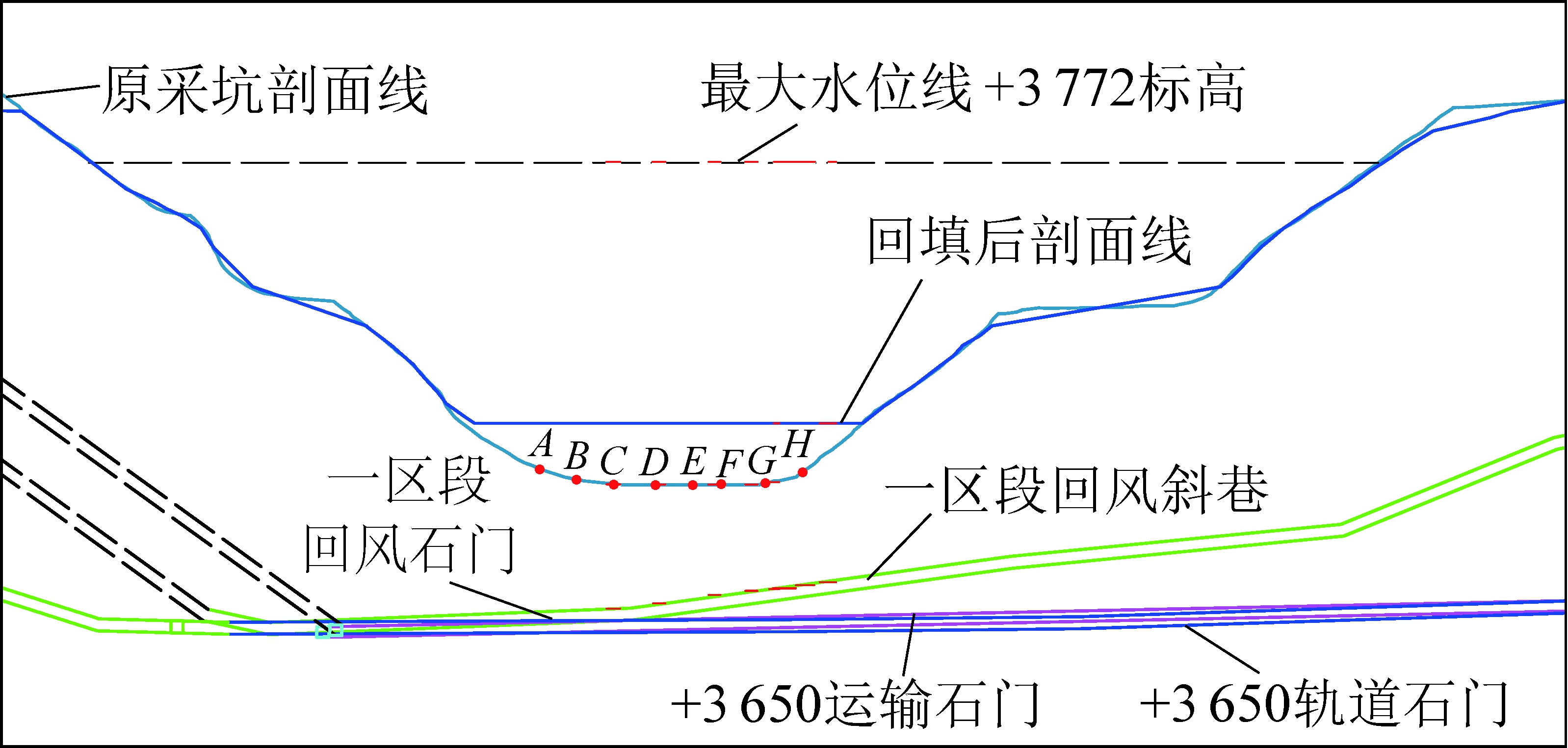
图9 Ⅰ—Ⅰ采坑回填后剖面图
Fig.9 Ⅰ—Ⅰ cross-section of open-pit after backfilling

图10 Ⅱ—Ⅱ采坑回填后剖面图
Fig.10 Ⅱ—Ⅱ cross-section of open-pit after backfilling
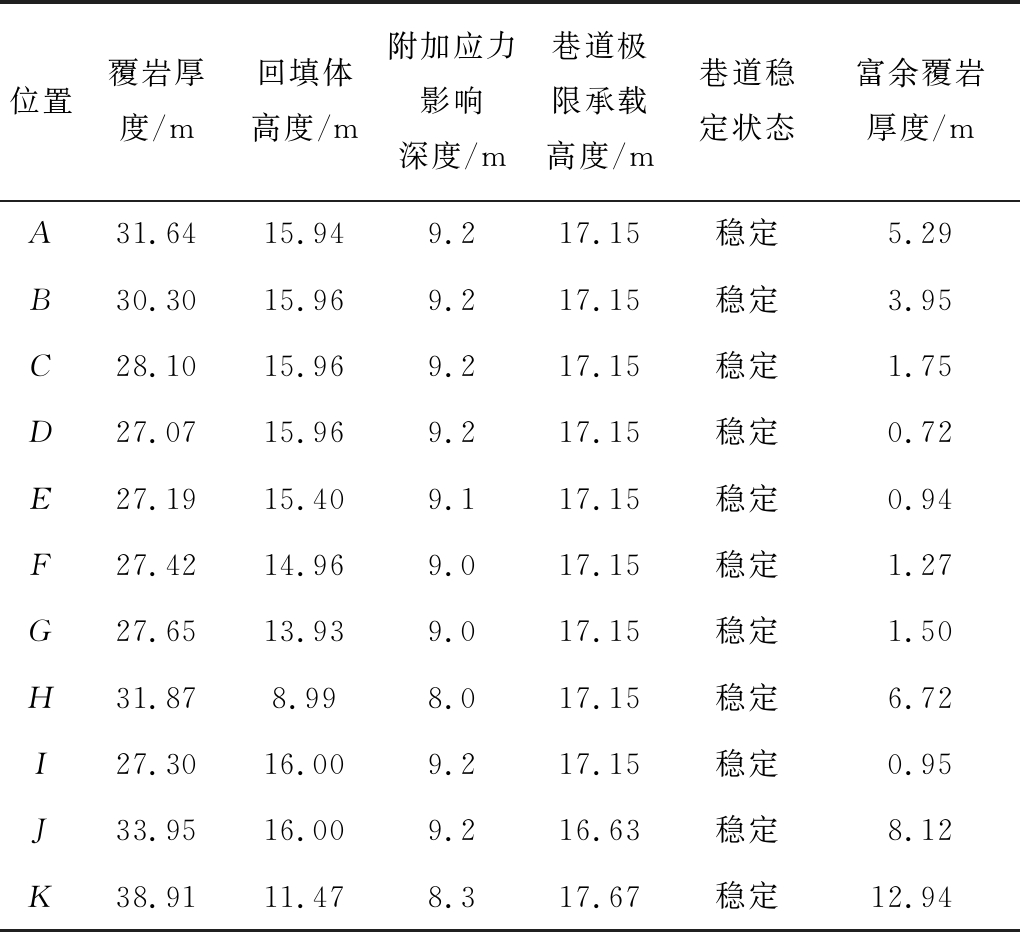
考虑到回填后采坑内积水需要一定时间才能达到预计标高,先按“回填体+车辆载荷”计算的最大附加应力影响深度及巷道稳定状态见表1。
由表1,虽然一区段回风斜巷能保持整体稳定,但局部D点、E点和I点的安全覆岩厚度不足1 m。
表1 考虑回填体和车辆载荷时巷道稳定状态
Table 1 Stability state of roadway under backfilling and vehicles load
位置覆岩厚度/m回填体高度/m附加应力影响深度/m巷道极限承载高度/m巷道稳定状态富余覆岩厚度/mA31.6415.949.217.15稳定5.29B30.3015.969.217.15稳定3.95C28.1015.969.217.15稳定1.75D27.0715.969.217.15稳定0.72E27.1915.409.117.15稳定0.94F27.4214.969.017.15稳定1.27G27.6513.939.017.15稳定1.50H31.878.998.017.15稳定6.72I27.3016.009.217.15稳定0.95J33.9516.009.216.63稳定8.12K38.9111.478.317.67稳定12.94
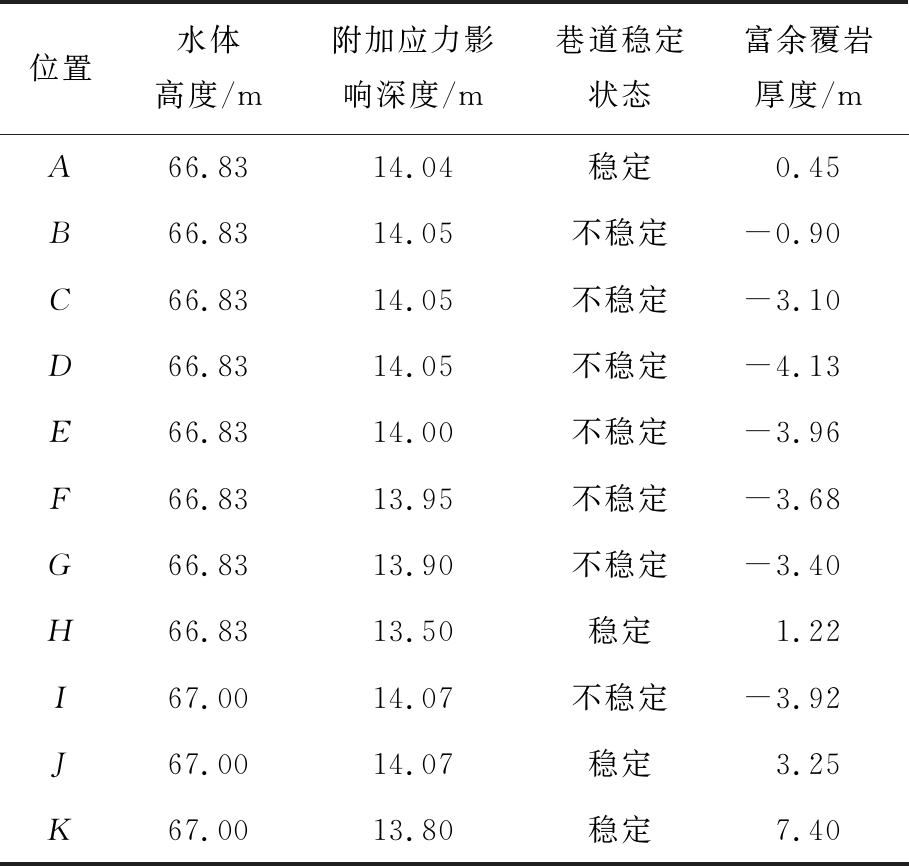
考虑回填后采坑最终积水到+3 772 m标高,按“回填体+车辆+水体载荷”计算的最大附加应力影响深度及巷道稳定状态见表2。
表2 考虑回填体、车辆和水体载荷时巷道稳定状态
Table 2 Stability state of roadway under backfilling, vehicles and water load
位置水体高度/m附加应力影响深度/m巷道稳定状态富余覆岩厚度/mA66.8314.04稳定0.45B66.8314.05不稳定-0.90C66.8314.05不稳定-3.10D66.8314.05不稳定-4.13E66.8314.00不稳定-3.96F66.8313.95不稳定-3.68G66.8313.90不稳定-3.40H66.8313.50稳定1.22I67.0014.07不稳定-3.92J67.0014.07稳定3.25K67.0013.80稳定7.40
由表2,考虑水体载荷后,一区段回风斜巷在A点和H点之间都处于不稳定状态。
采用数值模拟软件FLAC3D7.0对回填前、后和采坑积水条件下岩体破坏区进行了模拟,模型如图11所示。巷道考虑支护条件,采用pile结构单元进行支护模拟。采坑积水载荷按照水体在回填体和坡体上方的高度产生的水压施加地表边界条件,如图11c所示。图12为模拟得到的回填前、回填后和采坑积水条件下岩体破坏区分布情况。如图12所示,回填前,巷道覆岩在起坡后55 m范围出现塑性区,塑性区高度没有波及到地表;回填后的巷道覆岩塑性区范围和高度增加,但仍然没有到达地表;回填地表积水后,巷道覆岩塑性区水平范围进一步增加到约60 m,回填体的破坏深度与覆岩破坏高度几乎沟通,巷道具有失稳风险,与理论计算的结论相符。需要采取措施保证井工巷道安全。
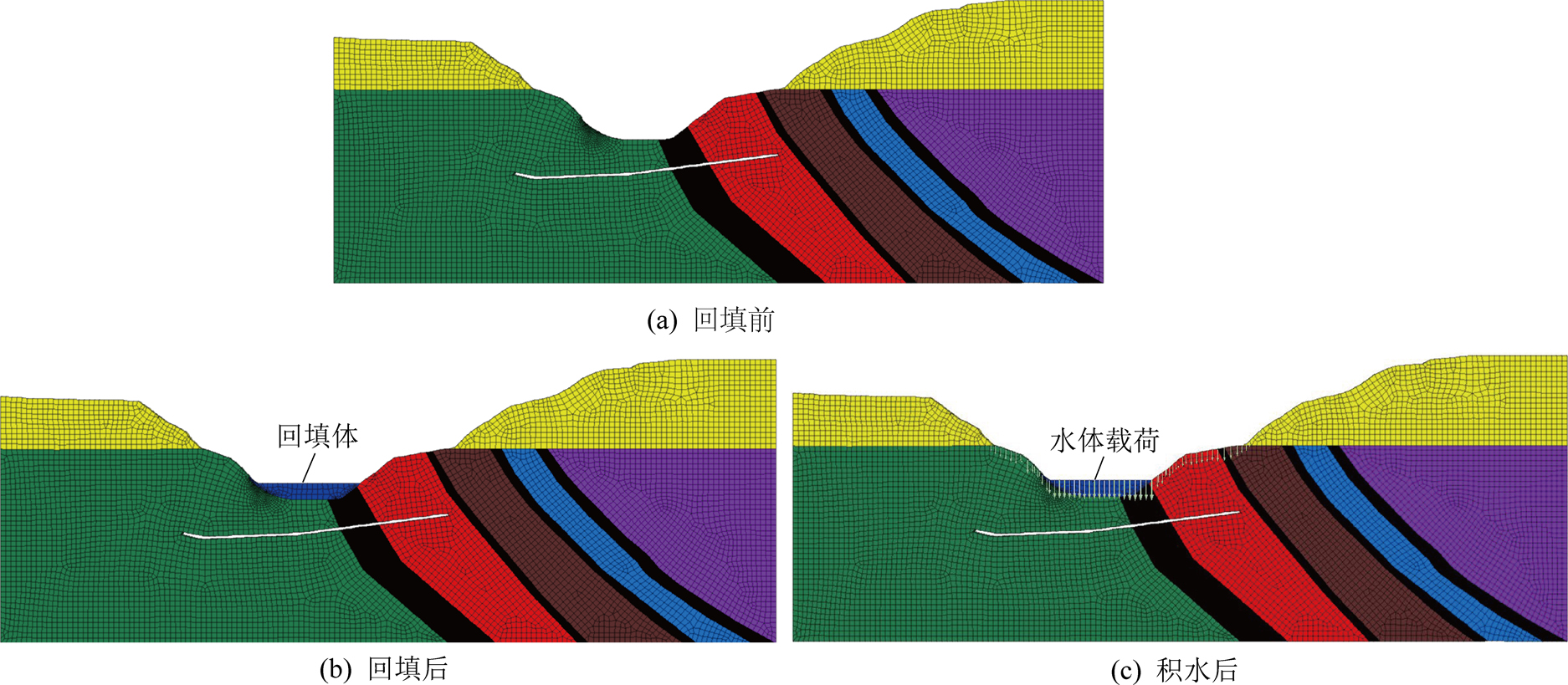
图11 采坑回填前后数值计算模型
Fig.11 Numerical simulation models before and after backfilling the open-pit
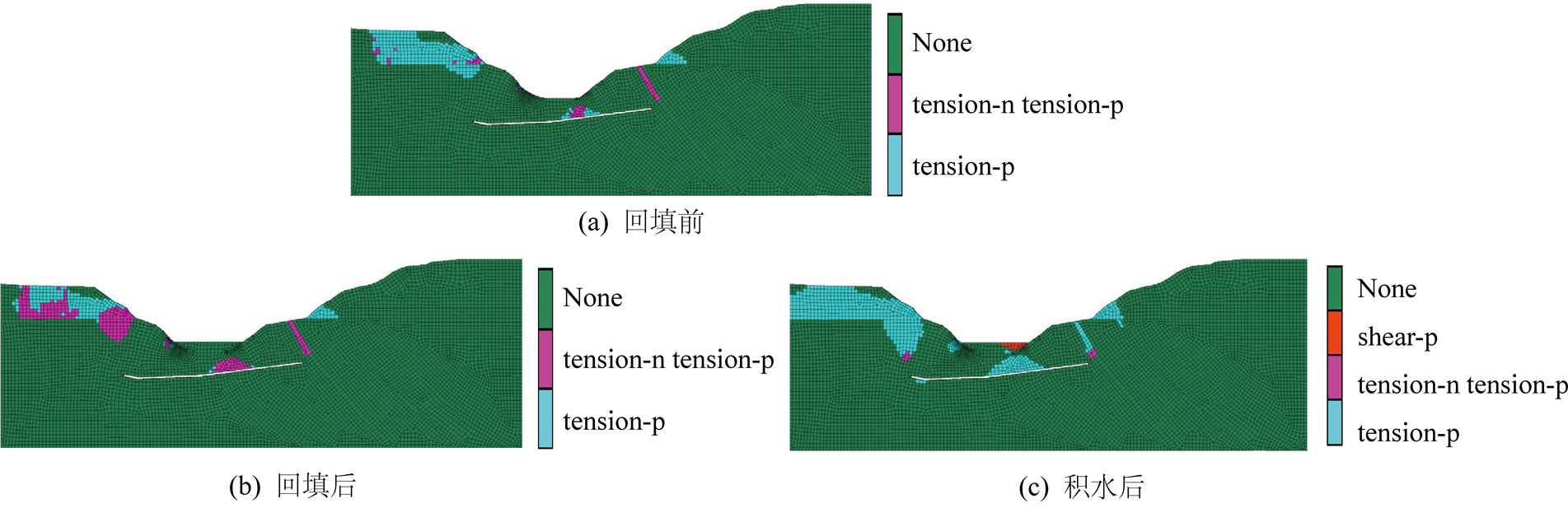
图12 采坑回填前后巷道覆岩破坏状况
Fig.12 Failure state of overlying strata over the roadway before and after backfilling the open-pit
采坑回填施工过程中,回填的区域、方向、回填的厚度及层次都会对下部井工巷道产生扰动作用,施工不当可能产生不均匀应力、偏应力、应力集中等对巷道稳定不利的影响。如图13所示,将地面回填区域按照对应地下井巷区域划分为4个分区(回填区域1、回填区域2、回填区域3、回填区域4),每个区域进行分层回填,为了使回填压力逐渐对称施加到井巷顶部,采用双向对称回填,在分区分层双向对称回填过程中,首先采用较缓的边坡角度进行推进覆盖,慢慢推进到井工区域,再逐步回填到设计标高+3 705 m,使基底应力逐渐加大到最终状态。
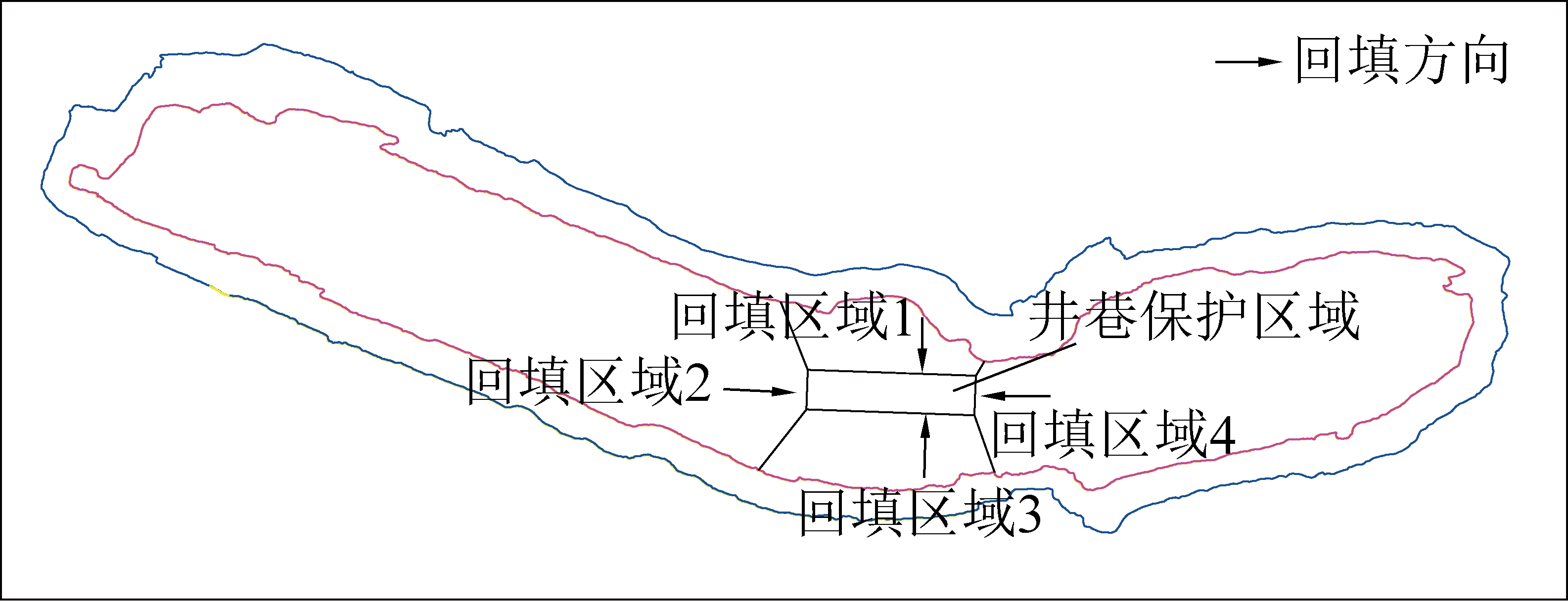
图13 地面回填分区及回填方向
Fig.13 Surface backfilling sections and directions
在井下巷道采用注浆锚索进行加强支护,根据理论计算和数值模拟结果,加强支护范围为一区段回风斜巷起坡后水平投影长度60 m范围,如图14所示。
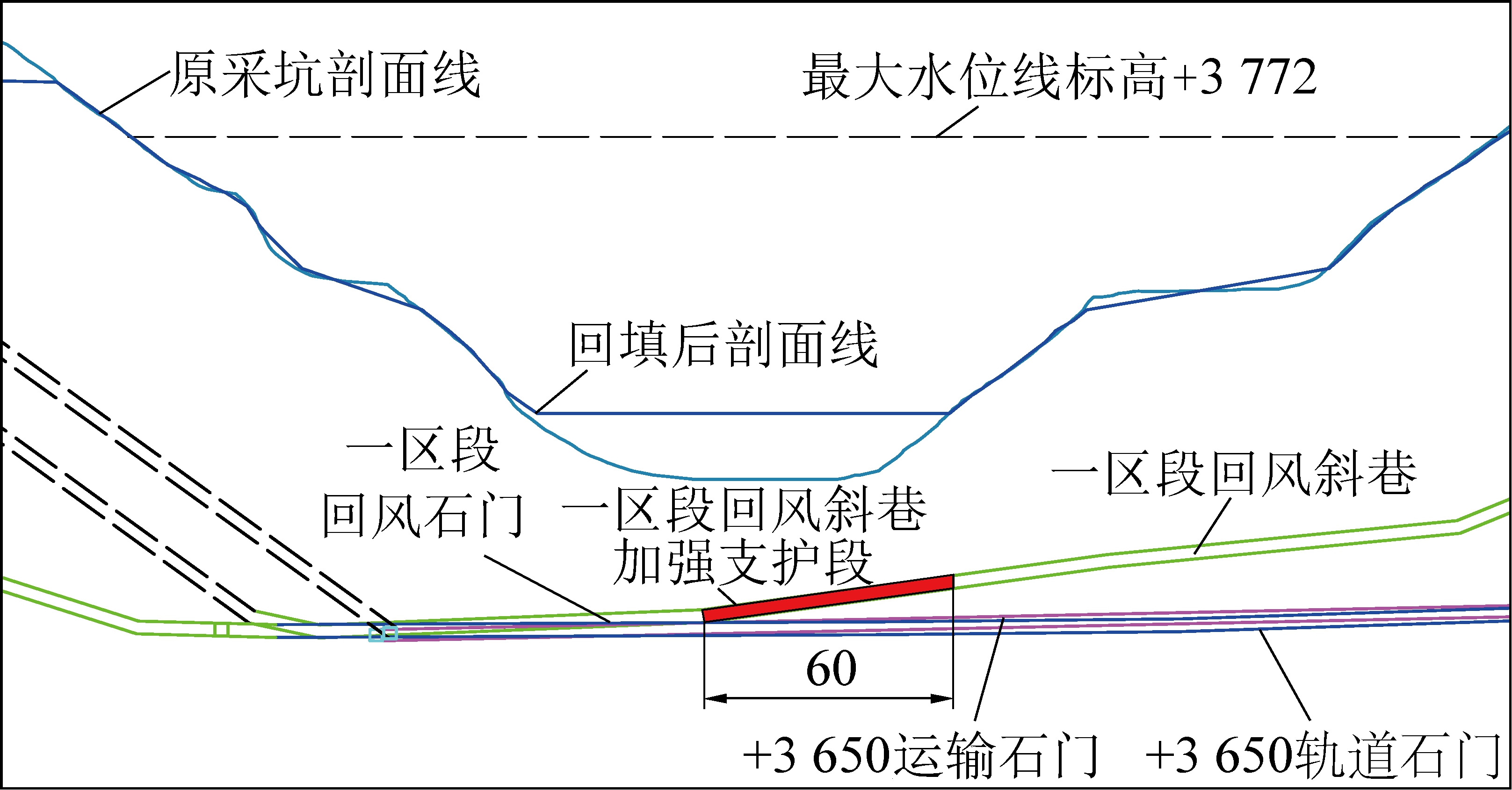
图14 巷道加强支护段范围
Fig.14 Reinforcement supporting range of roadway
1)露井联合矿区露天采坑回填会对其下方浅埋巷道的稳定性产生影响,主要影响因素包括:回填体载荷、车辆载荷和水体载荷。
2)采用弹性力学计算了回填体载荷、车辆载荷和水体载荷产生的最大附加应力,以最大附加应力达到自重应力10%时的深度作为附加应力影响深度;采用极限平衡理论计算了巷道极限承载覆岩高度。
3)通过比较最大附加应力影响深度与巷道极限承载覆岩高度之和与实际覆岩厚度的大小,评价了巷道不同位置处的稳定性。
4)根据稳定性评价和数值模拟结果,确定了地面回填保护巷道范围和井下巷道加强支护范围,提出了地面分区分层双向对称回填和井下锚注加强和监测相结合的巷道保护方法。
[1] 石中平. 垂直均布荷载矩形基础地基任意点附加应力系数公式推导[J]. 成都理工大学学报(自然科学版),2015,42(2):244-256.
SHI Zhongping. Formula derivation of additional stress coefficient at any point in rectangular foundation subsoil under vertical even load[J]. Journal of Chengdu University of Technology(Science & Technology Edition),2015,42(2):244-256.
[2] 王甲春,陈 峰. 地基中附加应力分布规律分析[J].湖南科技大学学报(自然科学版),2014,29(4):65-68.
WANG Jiachun, CHEN Feng. Analysis of foundation additional stress distribution[J]. Journal of Hunan University of Science & Technology(Nature Science Edition),2014,29(4):65-68.
[3] 张华磊,王连国. 采动底板附加应力计算及其应用研究[J].采矿与安全工程学报,2011,28(2):288-292.
ZHANG Hualei, WANG Lianguo. Computation of mining induced floor additional stress and its application[J]. Journal of Mining & Safety Engineering,2011,28(2):288-292.
[4] 张俊英. 地表新增荷载对采空区上方覆岩的影响规律[J]. 煤炭学报,2008,33(2):166-170.
ZHANG Junying. The laws of overlying strata influenced by newly increased load on the surface above worked out area[J]. Journal of China Coal Society,2008,33(2):166-170.
[5] 贾新果. 废弃巷道上方地表建筑场地地基稳定性评估[J]. 煤矿开采,2014,19(6):84-86.
JIA Xinguo. Evaluation of foundation stability of construction site over abandoned roadway[J]. Coal Mining Technology, 2014,19(6):84-86.
[6] 郭广礼,张国信,刘丙方. 地面荷载对地下采空区的临界扰动深度及其影响[J]. 矿山压力与顶板管理,2004(1):72-77.
GUO Guangli, ZHANG Guoxin, LIU Bingfang. Critical disturbance depth of surface load and its influence on underground mined gob[J]. Underground Pressure and Roof Control,2004(1):72-77.
[7] 魏 星,王 刚. 多轮组车辆荷载下公路地基的附加动应力[J]. 岩土工程学报,2015,37(10):1924-1930.
WEI Xing, WANG Gang. Induced dynamic stresses in subsoil of road subjected to moving vehicle load with wheel groups[J]. Chinese Journal of Geotechnical Engineering, 2015,37(10):1924-1930.
[8] 周凤玺,曹永春,赵王刚. 非均匀地基在矩形移动荷载作用下的动力响应[J]. 兰州理工大学学报,2015,41(2):122-126.
ZHOU Fengxi, CAO Yongchun, ZHAO Wanggang. Dynamic response of non-homogeneous foundation to rectangular moving loads[J]. Journal of Lanzhou University of Technology, 2015,41(2):122-126.
[9] 刘萌成,彭卫兵,高玉峰. 移动条形荷载作用下弹性层状介质动应力解析解[J]. 土木工程学报,2010,43(3):81-87.
LIU Mengcheng, PENG Weibing, GAO Yufeng. Analytical solution of the dynamic stress of elastic multi-layered medium under moving strip load[J]. China Civil Engineering Journal, 2010,43(3):81-87.
[10] 刘 伟,汤连生,张庆华. 车辆动载下路基土竖向动应力及扩散规律[J]. 重庆交通大学学报(自然科学版),2012,31(4):799-802.
LIU Wei, TANG Liansheng, ZHANG Qinghua. Research on dynamic stress of subgrade soil under vehicle loads and its diffused rule[J]. Journal of Chongqing Jiaotong University(Natural Science), 2012,31(4):799-802.
[11] 罗红星,但路昭,秦雨樵. 车辆荷载对浅埋大断面隧道围岩的影响研究[J]. 水利与建筑工程学报,2017,15(2):100-104.
LUO Hongxing, DAN Luzhao, QIN Yuqiao. Influence of vehicle load on large-section tunnels in shallow rock mass[J]. Journal of Water Resources and Architectural Engineering, 2017,15(2):100-104.
[12] 杨强强,丁小军,王 旭,等. 车辆荷载作用下黄土路基竖向土压力传递规律研究[J]. 公路交通科技,2021,38(2):40-46.
YANG Qiangqiang, DING Xiaojun, WANG Xu, et al. Study on vertical earth pressure transfer rule of loess subgrade under vehicle loading[J]. Journal of Highway and Transportation Research and Development,2021,38(2):40-46.
[13] 孟上九,程有坤. 车辆荷载作用下季冻土路基永久变形研究综述[J]. 哈尔滨理工大学学报,2014,19(2):1-5.
MENG Shangjiu, CHENG Youkun. The review on permanent deformation of seasonal frozen soil subgrade under the action of vehicle load[J]. Journal of Harbin University of Science and Technology,2014,19(2):1-5.
[14] 黎 冰,高玉峰,魏代现,等. 车辆荷载的影响深度及其影响因素的研究[J]. 岩土力学,2005,26(S2):311-313.
LI Bing, GAO Yufeng, WEI Daixian, et al. Research on influential depth of vehicle loads and its influencing factors[J]. Rock and Soil Mechanics, 2005,26(S2):311-313.
[15] 孙吉书,梅林健,杨 辉. 施工车辆荷载对低路堤软土地基的影响深度分析[J]. 河北工业大学学报,2018,47(4):93-97.
SUN Jishu, MEI Linjian, YANG Hui. Analysis on influence depth of construction vehicle load in low embankment soft subsoil[J]. Journal of Hebei University of Technology, 2018,47(4):93-97.
[16] 黄庆享,刘玉卫. 巷道围岩支护的极限自稳平衡拱理论[J].采矿与安全工程学报,2014,31(3):354-358.
HUANG Qingxiang, LIU Yuwei. Ultimate self-stable arch theory in roadway support[J]. Journal of Mining & Safety Engineering,2014,31(3):354-358.
[17] 马振乾,姜耀东,杨英明,等. 芦岭矿近距离煤层重复开采下底板巷道稳定性研究[J]. 岩石力学与工程学报,2015,34(S1):3320-3327.
MA Zhenqian, JIANG Yaodong, YANG Yingming, et al. Floor roadway stability in repeated mining of close distance coal seams in Luling Coal Mine[J]. Chinese Journal of Rock Mechanics and Engineering,2015,34(S1):3320-3327.
[18] 谷拴成,史向东,王恩波. 层状岩体中矩形巷道顶板破坏高度[J]. 煤矿安全,2014(12):61-67.
GU Shuancheng, SHI Xiangdong, WANG Enbo. Roof Failure Height of Rectangular Roadway in Bedded Rock[J].Safty in Coal Mines,2014(12):61-67.
[19] 谷拴成,樊 琦,王建文,等. 层状岩体巷道顶板冒落拱高度计算方法研究[J]. 煤炭工程,2012(12):73-76.
GU Shuancheng, FAN Qi, WANG Jianwen, et al. Calculation method of caving arch height of bedded rock roadway[J]. Coal Engineering,2012(12):73-76.
[20] 徐佑林,潘瑞凯,张瑞君. 跨石门开采巷内加强支护技术研究[J]. 煤炭科学技术,2019,47(8):46-51.
XU Youlin, PAN Ruikai, ZHANG Ruijun. Research on strengthening support technology in roadway crosscut mining[J]. Coal Science and Technology,2019,47(8):46-51.