0 引 言
煤层瓦斯含量是预测矿井瓦斯涌出量、煤矿瓦斯危险程度评价以及煤层气资源勘探开发的重要依据之一[1-3]。煤层瓦斯含量影响因素众多,各因素具有复杂性、非线性、动态性和随机不确定性等特点,使得准确预测煤层瓦斯含量较为困难。为解决该问题,基于案例分析的瓦斯地质数学模型法[4-5]得到了快速发展,该方法主要是借助于机器学习算法、数据挖掘技术等数学工具,通过分析与瓦斯含量相关的数据,建立考虑多因素动态变化的瓦斯含量预测模型。
近年来,BP神经网络[6-7]、支持向量回归机[8-10]、线性回归等[11]方法被广泛应用于瓦斯含量预测。此外,周鑫隆等[12-13]采用灰熵分析法以及径向基函数模型进行瓦斯含量预测,谷松等[14]将灰色理论引入小波神经网络对煤层瓦斯含量进行预测。HAO等[15]基于量化理论建立了瓦斯含量预测模型。姜家钰等[16]提出利用工作面瓦斯涌出量反演煤层原始瓦斯含量技术和基于探采对比的煤层瓦斯含量预测方法。
上述煤层瓦斯含量预测模型及方法均存在一定的适用范围,其普遍适用性需要进一步研究。针对此,笔者建立了包含有35组瓦斯含量实例的数据模型,采用全子集回归、随机森林(Random Forest,RF)2种特征选择方法,确定了最优的瓦斯含量参数组合;利用高斯回归过程(Gaussian Process Regression,GPR)、最小二乘支持向量机(Least Square Support Vector Machine,LS-SVM)、梯度提升回归树(Gradient Boosting Regression Tree,GBRT)以及极限学习机(Extreme Learning Machine,ELM)等4种常用经典机器学习算法,构建了多参数组合预测模型,并采用判定系数(R2)、归一化均方误差(Nmse)、希尔不等系数(Tic)、平均绝对误差(Af)以及平均相对误差(Ae)对模型预测性能进行综合评估,提升了瓦斯含量预测模型的准确性和科学性。
1 瓦斯含量预测数据处理
1.1 瓦斯含量预测数据实例获取
以贵州某矿二采区16煤层为研究对象,该煤层为煤与瓦斯突出危险煤层,Ⅲ类不易自燃。煤层瓦斯含量与埋深、煤厚、底板标高、主断层水平距离、顶板岩性、底板岩性、褶皱、水分、灰分、挥发分、孔隙率等因素有关,并在各类瓦斯含量预测中广泛采用[17-18]。因此,笔者构建的煤层瓦斯含量预测指标为表征测点煤层地质因素的埋深(X1)、煤厚(X2)、底板标高(X3)、与主断层水平距离(X4)、顶板岩性(X5)、底板岩性(X6)、褶皱(X7)以及表征煤层自身特性的水分(X8)、灰分(X9)、挥发分(X10)、孔隙率(X11),数据见表1(由于篇幅所限,仅列出前后5组数据),其中前28组作为训练集,后7组作为验证集。煤层瓦斯含量与各量化因素关系如图1所示。
表1 煤层瓦斯含量及影响因素数据
Table 1 Data of coal gas content and influencing factors
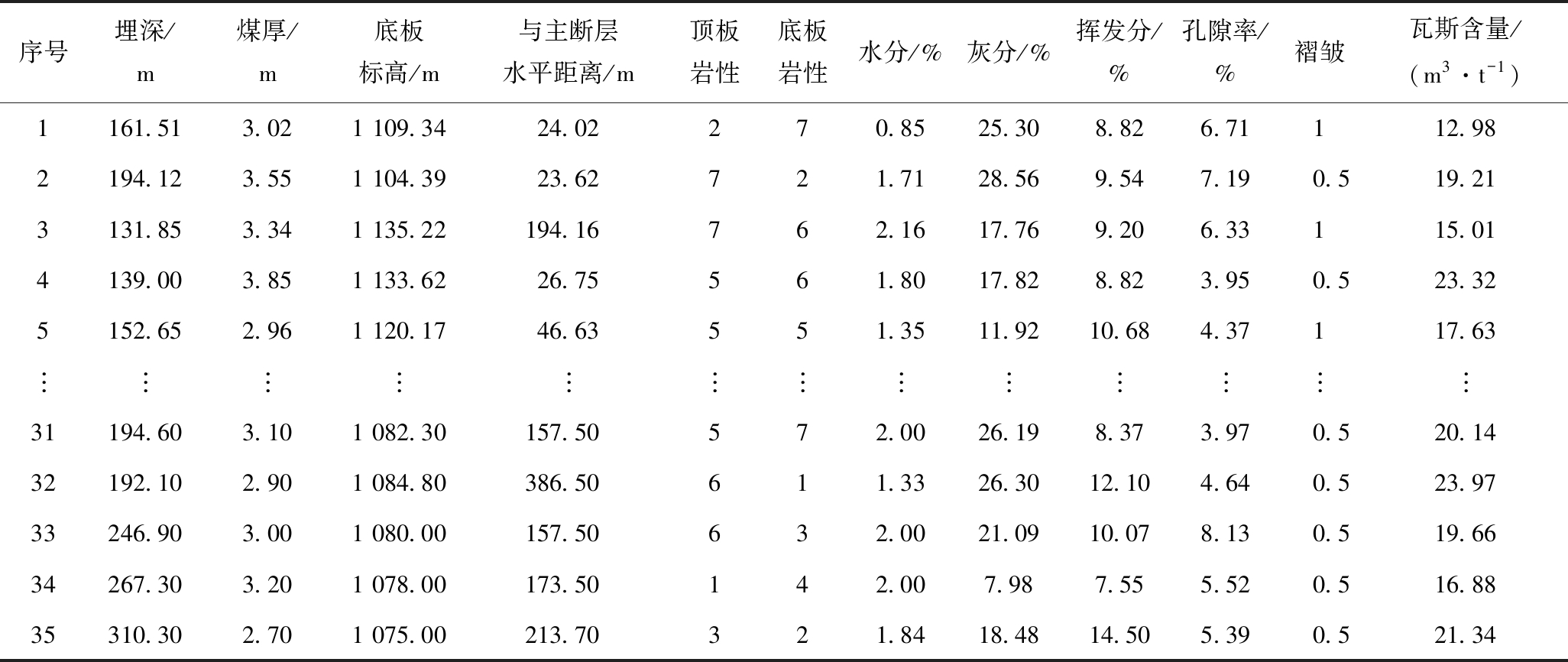
序号埋深/m煤厚/m底板标高/m与主断层水平距离/m顶板岩性底板岩性水分/%灰分/%挥发分/%孔隙率/%褶皱瓦斯含量/(m3·t-1)1161.513.021 109.3424.02270.8525.308.826.71112.982194.123.551 104.3923.62721.7128.569.547.190.519.213131.853.341 135.22194.16762.1617.769.206.33115.014139.003.851 133.6226.75561.8017.828.823.950.523.325152.652.961 120.1746.63551.3511.9210.684.37117.63︙︙︙︙︙︙︙︙︙︙︙︙︙31194.603.101 082.30157.50572.0026.198.373.970.520.1432192.102.901 084.80386.50611.3326.3012.104.640.523.9733246.903.001 080.00157.50632.0021.0910.078.130.519.6634267.303.201 078.00173.50142.007.987.555.520.516.8835310.302.701 075.00213.70321.8418.4814.505.390.521.34
注:根据煤层透气性,对顶板岩性以及底板岩性进行定量描述,透气性最好的粉砂岩用1表示,透气性最差的泥岩用7表示,细砂岩、泥质粉砂岩、砂质泥岩、碳质泥岩、铝质泥岩分别用2、3、4、5、6表示;对于褶皱,以取样点附近褶皱较发育的用1表示,不发育的用0.5表示。
由图1可知,煤层瓦斯含量与埋深、煤厚、底板标高、与主断层水平距离、水分、灰分、挥发分及孔隙率的线性判定系数较低(R2=0.001~0.089),煤层瓦斯含量与各因素不存在明显的线性关系。

图1 瓦斯含量与各量化指标线性拟合示意
Fig.1 Linear relationship fitting diagram between gas content and quantitative indexes
1.2 数据标准化处理
为确保模型预测效果,需在模型构建前对数据进行预处理。由于现有实例中选用的11个影响煤层瓦斯含量的因素均是数值型数据,如果直接用原始指标值进行分析,高数量级的指标在综合分析中作用会加大,而低数量级的指标在综合分析中作用就会减小。为保证发挥各个因素作用,对其进行零-均值规范化(z-score标准化)处理,即对各因素的数据集x1,x2,…,xn经过式(1)—式(3)标准化变换,得到介于0~1的新序列,各因素新序列的数量级相同,以减少不同因素数值量级之间差距对模型的影响。
(1)
(2)
(3)
式中:xi为原始序列,![]() 为序列平均值;s为方差;hi为变换后新序列,i∈[1,n]。
为序列平均值;s为方差;hi为变换后新序列,i∈[1,n]。
2 煤层瓦斯含量预测模型建立流程及初选
2.1 预测模型建立流程
煤层瓦斯含量预测模型建立流程如图2所示。

图2 预测模型建立流程
Fig.2 Establish flow chart of prediction model
1)样本数据处理。对数据集进行标准化。
2)融合模型初选。采用特征选择算法获取不同特征参数组合;利用不同有监督算法与特征参数组合,建立瓦斯含量预测模型。
3)融合模型优选。不同算法对瓦斯含量特征参数组合的预测性能不同,对验证集数据进行分析,选择平均判定系数![]() 的算法[19]以及特征参数组合,选择预测模型;在上述预测模型中,选择Nmse≤0.01且Tic≤0.01的预测模型[20-21]作为优化模型。
的算法[19]以及特征参数组合,选择预测模型;在上述预测模型中,选择Nmse≤0.01且Tic≤0.01的预测模型[20-21]作为优化模型。
4)融合模型验证。对优化模型各组预测数据取平均计算后得到预测值![]() 并采用验证集进行对比分析。
并采用验证集进行对比分析。
2.2 预测模型初选
2.2.1 煤层瓦斯含量特征参数组合
研究表明,机器学习过程中过少的变量将导致模型的低准确率,过多参量也不一定会增加模型准确度,还容易导致过拟合;不同煤层瓦斯含量预测指标在特征选择方法下称为特征参数,而不同特征参数组合对各类机器学习算法敏感性有差异。因此,煤层瓦斯含量特征参数组合采用全子集回归以及随机森林2种特征选择方法,根据特征的重要性或组合效果选择出一系列特征子集。
全子集筛选是基于不同自变量的所有可能的组合方式,对缩减后的变量组合通过最小二乘法进行拟合,并在所有可能的模型中选择校正R2大于0.900的模型[22],特征选择结果如图3a所示,即16种最优组合。
随机森林采用大量的决策树进行特征选择,将每棵决策树得到的变量综合性进行综合分析,得到最终的变量重要性排序,如图3b所示。在本例中,根据均方误差及残差平方和,最终选择除主断层水平距离、褶皱以及灰分外的8种因素。
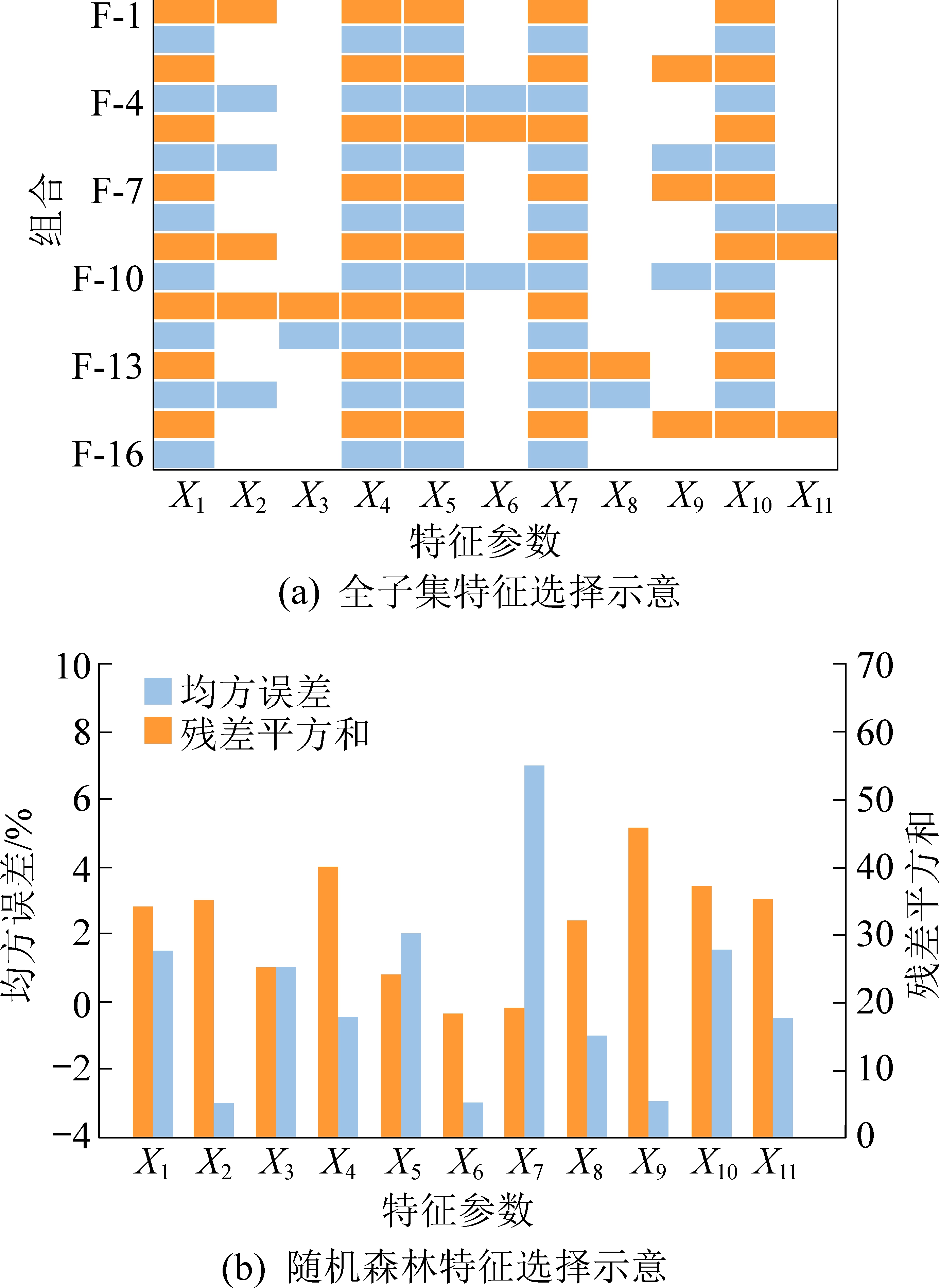
图3 特征选择各方法结果
Fig.3 Results of feature selection methods
经上述全子集回归法以及随机森林法对11种影响煤层瓦斯含量的参数进行不同规律选择, 17种特征参数组合见表2,其中F-1—F-16为全子集筛选,F-17为随机森林筛选。“☆”代表该组合选中的特征参数。
表2 瓦斯含量特征参数组合
Table 2 Combination of gas content characteristic parameter

组合X1X2X3X4X5X6X7X8X9X10X11F-1☆☆☆☆☆☆F-2☆☆☆☆☆F-3☆☆☆☆☆☆F-4☆☆☆☆☆☆☆F-5☆☆☆☆☆☆F-6☆☆☆☆☆☆☆F-7☆☆☆☆☆F-8☆☆☆☆☆☆F-9☆☆☆☆☆☆☆F-10☆☆☆☆☆☆☆F-11☆☆☆☆☆☆☆F-12☆☆☆☆☆☆F-13☆☆☆☆☆☆F-14☆☆☆☆☆☆ ☆F-15☆☆☆☆☆☆☆F-16☆☆☆☆F-17☆☆☆☆☆☆☆☆
2.2.2 瓦斯含量预测模型初选
笔者采用4种有监督学习算法对煤层瓦斯含量数据集进行学习,其中包括高斯过程回归(GPR)、最小二乘支持向量机(LS-SVM)、梯度提升回归树(GBRT),以及极限回归机(ELM)。
高斯过程回归(GPR)[23]对处理高维数、小样本、非线性复杂问题具有很好的适应性,且泛化能力强。与神经网络、支持向量机相比,该方法具有易实现、超参数自适应获取等优点。
最小二乘支持向量机[24-25](LS-SVM)优化问题的最终目的是得到优化模型参数,从而使LS-SVM构建的线性决策函数不仅拥有良好的拟合性能,而且模型泛化能力强。
梯度提升树(GBRT)[26]是提升法的一种,其每一次的计算是为了减少上一次的残差,在残差减少(负梯度)的方向上建立一个新的模型。该方法泛化能力和表达能力较好,具有较好的可解释性和鲁棒性,能够自动发现特征之间的高阶关系。
极限学习机(ELM)[27]是一类基于前馈神经网络构建的机器学习方法,其特点是隐含层节点的权重为随机或人为给定的,且不需要更新,学习过程仅计算输出权重。
通过17种不同特征参数组合采用4种不同有监督学习算法,构建了68种瓦斯含量预测模型,其判定系数R2见表3。R2计算方法为
(4)
式中:yi为真实值,![]() 为预测值,i∈[1,n]。
为预测值,i∈[1,n]。
不同算法采用不同特征参数组合时模型的判定系数R2为0.475~0.998,其中梯度提升回归树(GBRT)表现最好,R2均值为0.995。其次是最小二乘支持向量机(LS-SVM)算法,R2均值为0.988。再次为高斯过程回归(GPR),R2均值为0.731以及极限学习机(ELM),R2均值为0.659。梯度提升回归树(GBRT)和最小二乘支持向量机(LS-SVM)对特征参数的选择依赖性不强,不同特征参数组合下梯度提升回归树(GBRT)R2为0.986~0.998,最小二乘支持向量机(LS-SVM)的R2为0.964~0.992。高斯过程回归(GPR)以及极限学习机(ELM)在不同特征参数组合下其R2的波动较大,高斯过程回归(GPR)的R2为0.475~0.841,极限学习机(ELM)的R2为0.475~0.790。
由表3可知,F-3、F-5、F-6、F-7、F-8、F-10、F-11、F-12、F-13、F-15、F-16、F-17等12种特征参数组合的判定系数R2平均值均大于0.800,LS-SVM 和GBRT 的判定系数R2平均值均大于0.800,即LS-SVM和GBRT两种算法在本例中无论精度与波动性在何种参数组合下预测效果都比较理想。因此,初选得到瓦斯含量预测模型为LS-SVM和GBRT与上述12种特征参数的组合,共24个预测模型。
表3 不同算法采用不同特征参数组合时的判定系数R2
Table 3 Judgment coefficients R2 of different algorithms with different parameter combinations

参数组合各有监督学习算法判定系数R2GPRLS-SVMGBRTELM各个参数组合R2均值F-10.5110.9870.9950.6920.796F-20.6670.9890.9860.5510.798F-30.7520.9910.9970.7350.869F-40.4750.9910.9970.6900.788F-50.7730.9900.9970.6330.848F-60.7630.9910.9970.7210.868F-70.8310.9820.9970.7010.878F-80.7690.9910.9960.6240.845F-90.7170.9920.9970.4750.795F-100.8060.9910.9970.6190.853F-110.7470.9920.9980.7900.881F-120.7920.9910.9960.6970.869F-130.8090.9910.9940.6880.870F-140.6500.9820.9970.5420.793F-150.8410.9910.9950.5880.854F-160.7730.9640.9870.7840.877F-170.7490.9910.9960.6690.851各个算法R2均值0.7310.9880.9950.659—
3 煤层瓦斯含量预测模型优选及验证
3.1 煤层瓦斯含量预测模型优选
对24种初步选择得到的预测模型的Nmse以及Tic进行计算,计算公式如下
(5)

(6)
综合考虑Nmse≤0.01以及Tic≤0.01,得到特征选择与机器学习算法相融合的最优预测模型,如图4所示。由图4a可知,最小二乘支持向量机(LS-SVM)中除F-7、F-16外均满足设定要求。由图4b可知,梯度提升树(GBRT)中除F-16外其他特征组合模型均满足设定要求。通过上述方法可得到21组最优融合预测模型,包括LS-SVM与F-3、F-5、F-6、F-8、F-10、F-11、F-12、F-13、F-15、F-17(10类),GBRT与F-3、F-5、F-6、F-7、F-8、F-10、F-11、F-12、F-13、F-15、F-17(11类)。

图4 LS-SVM以及GBRT风向玫瑰图
Fig.4 Wind Rose map of LS-SVM and GBRT
3.2 最优融合预测模型验证
通过验证集的7组煤层瓦斯含量进行验证,预测结果评价指标见表4。由表4可知,所选择的21种模型对瓦斯含量的预测结果,Nmse≤0.01,Tic≤0.01。
表4 不同模型预测结果的评价指标对比
Table 4 Evaluation indexes comparison of prediction results with different models

序列模型NmseTicR2Af/(m3·t-1)Ae/%Emax/% 1GBRT与F-3组合0.0030.0050.9970.0930.501.632GBRT与F-5组合0.0030.0050.9970.1130.643.283GBRT与F-6组合0.0030.0040.9970.0910.482.314GBRT与F-7组合0.0030.0050.9970.1180.661.985GBRT与F-8组合0.0040.0060.9960.1100.582.356GBRT与F-10组合0.0030.0050.9970.0880.481.827GBRT与F-11组合0.0020.0040.9980.0860.461.718GBRT与F-12组合0.0040.0060.9960.1200.695.549GBRT与F-13组合0.0060.0070.9940.1140.642.9610GBRT与F-15组合0.0050.0070.9950.1090.602.4511GBRT与F-17组合0.0040.0060.9960.0820.441.7512LS-SVM与F-3组合0.0090.0090.9910.2431.343.6313LS-SVM与F-5组合0.0100.0090.9900.2451.353.7614LS-SVM与F-6组合0.0090.0080.9910.2291.253.5715LS-SVM与F-8组合0.0090.0080.9910.2321.273.6716LS-SVM与F-10组合0.0090.0090.9910.2401.313.6617LS-SVM与F-11组合0.0080.0080.9920.2231.223.4318LS-SVM与F-12组合0.0090.0090.9910.2461.364.2519LS-SVM与F-13组合0.0090.0090.9910.2351.283.5120LS-SVM与F-15组合0.0090.0080.9910.2291.253.5621LS-SVM与F-17组合0.0090.0080.9910.2361.283.56
通过式(7)、式(8)计算平均绝对误差(Af)及平均相对误差(Ae),得到上述21种最优融合模型中Af为0.082~0.246 m3/t,Ae为0.44%~1.36%,各模型最大相对误差(Emax)均小于10%。
(7)
(8)
以7组验证集为例,对21种最优融合模型各组预测数据取平均计算后,结果如图5所示,各评价指标值如下:

Nmse0.007Tic0.005R20.993Af/(m3·t-1)0.170Ae/%0.75Emax/%1.71
由图5及各评价指标值可知,各评估指标均符合笔者设定要求。

图5 预测数据与原始数据对比
Fig.5 Comparison of predicted data and original data
4 结 论
1)基于全子集回归法和随机森林法2种特征选择方法构建了17种瓦斯含量影响因素特征参数组合集,其中采用全子集回归法得到16种,采用随机森林法得到1种。
2)不同算法与特征参数组合下的68种瓦斯含量预测模型的R2为0.475~0.998,其中R2平均值大于0.800的算法有最小二乘支持向量机、梯度提升回归树。
3)最优融合预测模型包括LS-SVM与F-3、F-5、F-6、F-8、F-10、F-11、F-12、F-13、F-15、F-17,GBRT与F-3、F-5、F-6、F-7、F-8、F-10、F-11、F-12、F-13、F-15、F-17等21种;最终预测模型的Nmse为0.007,Tic为0.005,R2为0.993,Af为0.170 m3/t,Ae为0.75%,Emax为1.71%。
[1] 李成武,王义林,王其江,等.直接法瓦斯含量测定结果准确性实验研究[J].煤炭学报,2020,35(1):195-202.
LI Chengwu,WANG Yilin,WANG Qijiang,et al.Experimental study on accuracy of direct gas content determination[J].Journal of China Coal Society,2020,35(1):195-202.
[2] 马树俊,王兆丰,韩恩光,等.瓦斯含量测定中取心管管壁温度变化特性研究[J].煤炭科学技术,2020,48(6):95-101.
MA Shujun,WANG Zhaofeng,HAN Enguang,et al.Study on characteristics of temperature variation of coring tube wall during gas content determination process[J].Coal Science and Technology,2020,48(6):95-101.
[3] MAO Shanjun.Development of coal geological information technologies in China[J].Int J Coal Sci Technol,2020,7(2):320-328.
[4] 张子戌,袁崇孚.瓦斯地质数学模型法预测矿井瓦斯涌出量研究[J].煤炭学报,1999,24(4):34-38.
ZHANG Zixu,YUAN Chongfu.Study on mathematical model of coalbed gas geology used to prediction of mine gas emission[J].Journal of China Coal Society,1999,24(4):34-38.
[5] 张许良,单菊萍,彭苏萍.瓦斯含量及涌出量预测的数学地质技术与方法[J].煤炭学报,2009,34(3):350-354.
ZHANG Xuliang,SHAN Juping,PENG Suping.Mathematical geology technique and method for prediction of gas content and emission[J].Journal of China Coal Society,2009,34(3):350-354.
[6] 林海飞,高 帆,严 敏,等.煤层瓦斯含量PSO-BP神经网络预测模型及其应用[J].中国安全科学学报,2020,30(9):84-91.
LIN Haifei,GAO Fan,YAN Min,et al.Study on PSO-BP neural network prediction method of coal seam gas content and its application[J].China Safety Science Journal,2020,30(9):84-91.
[7] 汪吉林,翟建廷,秦 勇,等.淮北许疃矿抽采后瓦斯含量损失影响因素分析及预测[J].煤炭学报,2019,44(8):2401-2408.
WANG Jilin,ZHAI Jianting,QIN Yong,et al.Influencing factors analysis and prediction of the loss of gas content after gas drainage in Xutuan Mine of Huaibei,China[J].Journal of China Coal Society,2019,44(8):2401-2408.
[8] 魏国营,裴 蒙.基于PCA-AHPSO-SVR的煤层瓦斯含量预测研究[J].中国安全生产科学技术,2019,15(3):69-74.
WEI Guoying,PEI Meng.Prediction of coal seam gas content based on PCA-AHPSO-SVR[J].Journal of Safety Science and Technology,2019,15(3):69-74.
[9] LI Dong,PENG Suping,DU Wenfeng.New method for predicting coal seam gas content[J].Energy Sources,Part A:Recovery,Utilization,and Environmental Effects,2019,41(10):1272-1284.
[10] MENG Qian,MA Xiaoping,ZHOU Yan.Forecasting of coal seam gas content by using support vector regression based on particle swarm optimization[J].Journal of Natural Gas Science and Engineering,2014,21:71-78.
[11] 叶桢妮,侯恩科,段中会,等.郭家河煤矿回采工作面瓦斯涌出量预测[J].西安科技大学学报,2017,37(1):57-62.
YE Zhenni,HOU Enke,DUAN Zhonghui,et al.Prediction for gas emission quantity of the working face in Guojiahe coal mine[J].Journal of Xi′an University of Science and Technology,2017,37(1):57-62.
[12] 周鑫隆,汤 静,石必明,等.基于灰熵法的深部煤层瓦斯含量影响因素分析及预测[J].煤田地质与勘探,2016,44(2):19-23.
ZHOU Xinlong,TANG Jing,SHI Biming,et al.Analysis and forecast of influential factors of gas content in deep coal seam on the basis of the grey entropy[J].Coal Geology and Exploration,2016,44(2):19-23.
[13] 周鑫隆,章 光,吕 辰,等.深部煤层瓦斯含量的差值GM-RBF预测模型及其应用[J].安全与环境学报,2017,17(6):2050-2055.
ZHOU Xinlong,ZHANG Guang,LYU Chen,et al.A grey model for predicting the gas content in the deep coal seam and its application via the neural network of the difference radial basis function[J].Journal of Safety and Environment,2017,17(6):2050-2055.
[14] 谷 松,崔洪庆,冯文丽.基于灰色理论的小波神经网络对瓦斯涌出量的预测[J].煤炭学报,2007,32(9):964-966.
GU Song,CUI Hongqing,FENG Wenli.Mine gas gushing forecasting based on grey model and wavelet neural network[J].Journal of China Coal Society,2007,32(9):964-966.
[15] HAO Tianxuan,NIU Hao.Research on gas content prediction model of Hebi No.6 Mine based on Quantification Theory[J].Applied Mechanics and Materials,2014,535:614-621.
[16] 姜家钰,张玉贵,谢向向,等.基于探采对比的煤层瓦斯含量分析及预测[J].安全与环境学报,2015,15(3):25-28.
JIANG Jiayu,ZHANG Yugui,XIE Xiangxiang,et al.Method of gas content prediction based on measurement values of drilling exploration and gas parameters of mining practice[J].Journal of Safety and Environment,2015,15(3):25-28.
[17] 颜爱华.煤层瓦斯含量多源数据分析及其预测研究[D].北京:中国矿业大学(北京),2010.
[18] 李浩威.姚家山5号煤层瓦斯赋存规律及层次分析法在瓦斯灾害预测中的应用[D].徐州:中国矿业大学,2015.
[19] 黄 超,龚惠群.基于判定系数和趋势变动的时间序列逐段线性回归[J].统计与决策,2006,24(9):23-24.
HUANG Chao,GONG Huiqun.Piecewise linear regression of time series based on determination coefficient and trend changes[J].Statistics and Decision,2006,24(9):23-24.
[20] 金 鑫,王铁行,张 玉,等.计算黄土卸荷湿陷量的模量折减法研究[J/OL].岩石力学与工程学报:1-11[2021-02-13].https://doi.org/10.13722/j.cnki.jrme.2020.0783.
JIN Xin,WANG Tiehang,ZHANG Yu,et al.Method for calculating loess unloading collapse by using modulus reduction[J/OL].Chinese Journal of Rock Mechanics and Engineer ing:1-11[2021-02-13].https://doi.org/10.13722/j.cnki.jrme.2020.0783.
[21] 徐涵秋,孙凤琴,徐光志.高分五号高光谱AHSI和多光谱VIMI传感器数据的交互对比[J/OL].武汉大学学报(信息科学版):1-16[2021-02-13].https://doi.org/10.13203/ j.whugis20200586.
XU Hanqiu,SUN Fengqin,XU Guangzhi.Comparison of the Gaofen-5 AHSI and VIMI Sensors[J/OL].Geomatics and Information Science of University,Wuhan:1-16[2021-02-13].https://doi.org/10.13203/j.whugis20200586.
[22] 张智韬,韩 佳,王新涛,等.基于全子集-分位数回归的土壤含盐量反演研究[J].农业机械学报,2019,50(10):142-152.
ZHANG Zhitao,HAN Jia,WANG Xintao,et al.Soil salinity inversion based on best subsets-quantile regression model[J].Transactions of The Chinese Society of Agricultural Machinery,2019,50(10):142-152.
[23] JAMEI M,AHMADIANFAR I,OLUMEGBON I A,et al.On the assessment of specific heat capacity of nanofluids for solar energy applications:application of Gaussian Process Regression (GPR) Approach[J].The Journal of Energy Storage,2020,33:102067.
[24] XUE Xinhua,XIAO Ming.Deformation evaluation on surrounding rocks of underground caverns based on PSO-LSSVM[J].Tunnelling and Underground Space Technology,2017,69:171-181.
[25] HOU Enke,WEN Qiang,YE Zhenni,et al.Height prediction of water-flowing fracture zone with a genetic-algorithm support-vector-machine method[J].Int J Coal Sci Technol 2020,7(2):740-751.
[26] YU Zhenwei,KHURRAM Yousaf,MUHAMMAD Ahmad,et al.Efficient pyrolysis of ginkgo biloba leaf residue and pharmaceutical sludge (mixture) with high production of clean energy:Process optimization by particle swarm optimization and gradient boosting decision tree algorithm[J].Bioresource Technology,2020,304:123020.
[27] DU Han,SONG Danqing,CHEN Zhuo,et al.Prediction model oriented for landslide displacement with step-like curve by applying ensemble empirical mode decom-position and the PSO-ELM method[J].Journal of Cleaner Production,2020,267:122248.
