0 引 言
冲击地压是煤岩的突然动力失稳破坏,是煤矿深部开采面临的重大动力灾害之一。对于冲击地压发生机制的研究,首先是煤的冲击倾向性研究,冲击倾向性是煤岩积聚弹性能并发生突然失稳破坏的固有属性,已成为冲击地压预警与防治研究的基础[1]。
近年来,国内外学者对煤的冲击倾向性展开了大量的研究,主要分为3个方面:①煤层冲击倾向性新指标的研究;②冲击倾向性的影响因素研究;③不同冲击倾向性煤的受载响应特征研究。前两部分已取得众多研究成果,对于不同冲击倾向性煤受载响应特征的研究主要包括力学特性、声发射特性、电磁辐射特性、红外辐射特性等,窦林名等[2]研究了煤岩变形破坏峰值前后电磁辐射特征,得出电磁能量指数和电磁脉冲指数与现有的冲击倾向指标有很好的线性关系。赵毅鑫等[3]对冲击倾向性煤体破坏过程中的声热效应进行了研究,发现冲击倾向性煤体的失稳破坏更突然、更难以预测。李宏艳等[4]对不同冲击倾向性煤体进行了声发射试验,得出声发射能量与声发射b演化特征作为煤体失稳破坏的前兆信息。杨磊[5]研究得到了声发射能量特征与冲击倾向性呈正相关关系,并基于声发射定位演化研究了试样的破裂发展过程;杜伟升[6]基于忻州窑煤矿的冲击倾向性煤,研究了其非线性力学响应特征以及循环加卸载下的能量分配与演化规律。王岗等[7]研究了煤体冲击倾向性指标与破裂产生的电荷之间的关系,得出应力峰后电荷特征参数可作为煤体冲击倾向性强弱及冲击地压发生难易程度的判定依据。上述研究成果极大地丰富了煤的冲击倾向性理论,但对不同冲击倾向性煤破坏过程中的能量与损伤演化的研究成果相对较少,而能量驱动破裂失稳正是煤岩发生冲击破坏的本质。颗粒流模拟从细观力学出发,监测的能量种类全面,与力学试验相辅研究能量变化更加合理[8-9];在损伤破裂方面,颗粒流能够从细观层面实时再现岩石复杂的起裂和损伤行为,克服了AE监测噪声影响与内部微裂纹难以实时监测捕捉等技术难题[10-11],此外,针对冲击倾向性测定中8种无法判断的情况(4个指标中出现两强两弱和两弱两无的情况)和难以加工出规定数量标准试件的煤样,可研究探讨数值模拟方面的指标。
鉴于此,笔者在实验室冲击倾向性测试的基础上,利用PFC2D颗粒流数值软件开展煤样单轴压缩试验,研究不同冲击倾向性煤样受压破坏过程中的能量演化规律与损伤特征,探讨冲击倾向性判定的辅助指标,为煤体的冲击破坏机理与冲击危险预测提供理论依据。
1 试验与颗粒流模型建立
1.1 煤样冲击倾向性测试
试验煤样分别从强、弱、无冲击倾向性的3种煤层中选取同一煤层、同一批次的煤块进行制样,煤样主要取自我国的新疆、吉林和山东的煤矿,共进行了3组实验室测试。在进行冲击倾向性指标回归分析中,增加5组煤样的实验室测试数据,包含无、弱和强3种煤样,数据来源本实验室地质力学数据库。所有试样的制作及测试严格按照GB/T 23561—2009《煤和岩石物理力学性质测定方法》、GB/T 25217—2010《冲击地压测定、监测与防治方法》的相关部分规定执行,部分煤样的冲击倾向性指数与所需力学参数见表1,部分测试煤样结构如图1所示。

图1 部分煤样
Fig.1 Partial specimen
表1 部分煤样冲击倾向性与力学测试结果
Table 1 Bursting liability and mechanical test results of coal samples

煤样组号冲击倾向性4个指标(平均值)力学参数(平均值)单轴抗压强度/MPa冲击能量指数弹性能量指数动态破坏时间/ms综合评判结果弹性模量/GPa泊松比A33.235.157.2252强2.510.26B11.931.974.14359弱1.920.24C5.241.331.891130无0.970.24
1.2 颗粒流数值模型校核
颗粒流方法基于离散介质力学从细观尺度出发,采用颗粒组合成宏观物质,通过颗粒的运动及其相互作用来表现物质的宏细观力学行为,克服了传统连续介质力学模型的宏观连续性假设[12],适合模拟由矿物颗粒组成的材料。
在颗粒流程序中,颗粒与颗粒之间存在2种黏结模型:接触黏结模型和平行黏结模型[13]。接触黏结模型中的黏结只作用在2个颗粒之间的接触点上,只能传递力,常用于模拟散体材料,如土体;而平行黏结模型中的黏结是作用是在2个颗粒之间有限大小的圆截面上传递力和力矩,目前已被广泛应用于模拟煤岩类材料的力学性能[14]。因此,笔者采用PFC2D建立平行黏结模型开展数值模拟试验。
在采用离散元模拟煤岩变形破坏时,首先需要解决的问题就是获得准确可靠的细观参数,PFC2D中所使用的细观参数难以通过室内试验直接获取,而是通过与室内试验获得的单轴抗压强度、弹性模量、应力应变曲线等宏观力学参数进行对比,通过“试错法”不断调试来标定细观参数,使得建立的模型和室内试验所获得的宏观力学参数基本一致[14]。为此建立ø50 mm×100 mm的煤样数值模型,煤样密度1 300 kg/m3,颗粒最小半径0.3 mm,粒径比1.5,颗粒尺寸均匀分布,建立的PFC2D数值模型如图2a所示。通过赋予上下墙体恒定的速度进行轴向加载,直至试样破坏并使载荷达到设定值,实测与模拟的应力应变曲线如图2b所示,确定的模型细观参数及其数值计算结果见表2。通过应力应变曲线与表1、表2数据可以看出,数值模拟结果与室内试验吻合度较高,表明 PFC2D数值模拟结果与室内试验结果十分相近,在此基础上分析3种不同冲击倾向性煤的宏细观力学特性是可行的。
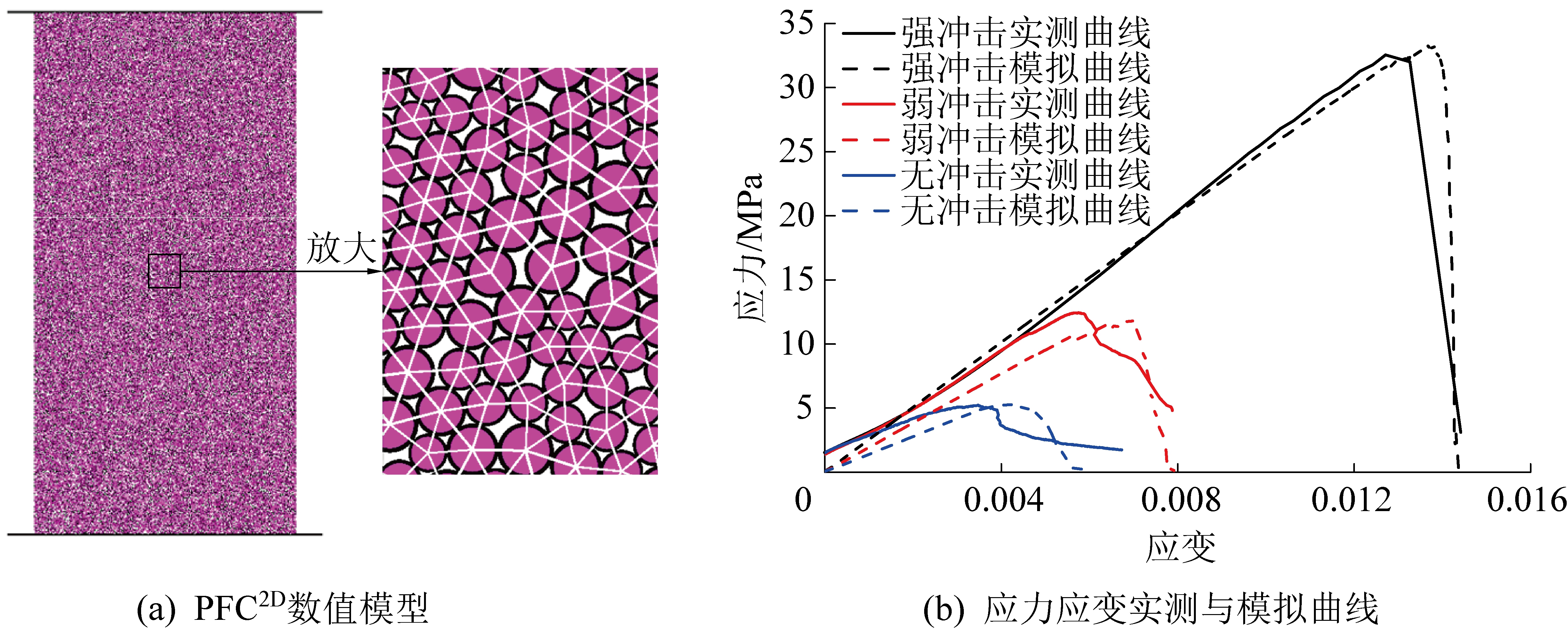
图2 建立的PFC2D数值计算模型与计算结果
Fig.2 PFC2D numerical calculation model and calculation results
表2 模型细观参数与计算结果
Table 2 Micro-mechanical parameters and simulation result

煤样组号细观颗粒参数接触模量/GPa接触刚度比平行黏结模量/GPa平行黏结刚度比法向黏结强度/MPa切向黏结强度/MPa内摩擦角/(°)宏观计算结果峰值强度/MPa弹性模量/GPa泊松比A1.7321.73220.7±0.541.4±0.5033.372.530.26B1.3721.3729.2±0.518.4±0.52011.861.870.24C0.8020.8024.0±0.28.0±0.2405.341.000.21
2 冲击倾向性与能量演化关系分析
热力学认为材料的破坏现象都是能量驱动下的失稳现象,PFC模拟中的能量分为模型组件能量与接触能量,在单轴压缩模型中,模型组件能量包括作用在墙体上的边界能、动能和阻尼能,接触能量包括应变能、阻尼能与滑动能。PFC模拟中充分考虑裂纹的影响,在接触断裂分离时,储存的应变能完全释放,其模拟的应变能更符合实际能量的变化,采用颗粒流模拟研究能量更具有优势[8]。
2.1 不同冲击倾向性煤的能量演化规律
将模拟中获得的能量按类别进行组合,最终分为5种能量,分别为边界能、应变能、耗散能、滑动摩擦能与动能,不同冲击倾向性煤应力应变过程中的各种能量演化情况如图3所示。
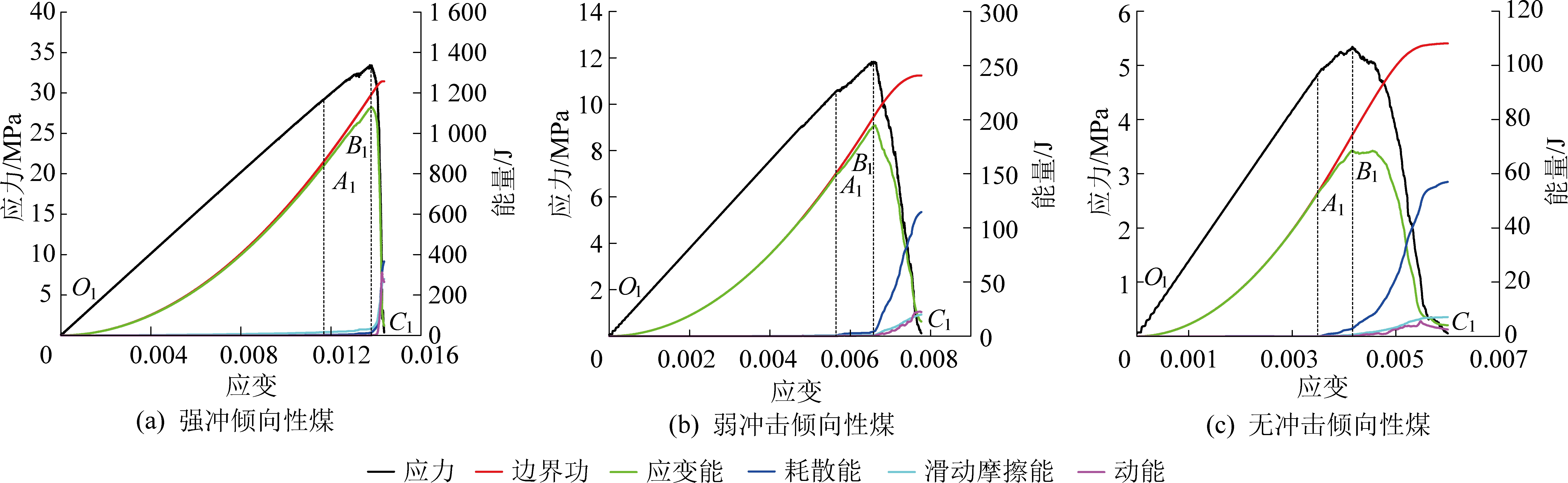
图3 不同冲击倾向性煤的能量演化与应力应变关系曲线
Fig.3 Relationships between energy and stress-strain of different bursting liability coals
由图3知,不同冲击倾向性煤的能量演化规律相似,在达到峰值强度前,作用在试样上下表面的边界能主要都转化为应变能,而耗散能、滑动能与动能的占比则非常小;峰值强度后,边界能继续增加,应变能快速释放,耗散能、滑动能与动能则开始迅速增长。根据应变能的演化特征,可将能量演化曲线分为3个阶段:
1)O1A1段:此阶段边界能和应变能2条曲线几乎重合,表明边界能几乎全部转化为应变能,而耗散能、滑动能与动能基本为零,到A1点时边界能与应变能两曲线出现了较小分离。该阶段应变能不断增长且增长速率逐渐增大,为应变能快速积聚的主要阶段,与应力应变过程中的压密阶段、弹性变形至微裂隙稳定发展阶段相对应。
2)A1B1段:A1点后边界能仍主要转化为应变能,应变能继续增大但其增速下降,并在峰值点B1附近增速减小为零。该阶段滑动能与耗散能占比逐渐增大,动能仍基本为零。该阶段与应力应变过程中的非稳定破裂发展阶段相对应。
3)B1C1段:到达峰值点B1时,应变能达到极值,之后应变能迅速释放降低至最小值,耗散能、滑动能与动能迅速增大并最终趋于稳定,该阶段为破裂后阶段。
对比上述3个阶段的节点与曲线走势可以发现,随着冲击倾向性的增强,峰值应变能与动能大幅增大,此外峰后应变能B1C1段的斜率与动能的增速也越大,表明应变能的释放更迅速,充分体现了强冲击倾向性煤具有积聚高应变能并快速释放的能力。
2.2 冲击倾向性能量新指标探讨
目前国标中评价煤的冲击倾向性指标主要为单轴抗压强度、冲击能量指数、弹性能量指数与动态破坏时间,当这4个指标出现两强两弱或两弱两无时,有8种无法判断的情况[15],此外对于难以加工出标准试件的煤样也无法进行冲击倾向性的判定,为此,在保证校核的基础上可探索数值模拟方面的指标。鉴于上文研究发现,应变能与动能与冲击倾向性呈正相关关系,笔者将从应变能释放与动能增加2个角度探索能够表征冲击倾向性的新指标。由于PFC数值模拟中采用恒定速率加载,因此可利用应变能-应变曲线、动能-应变曲线峰值后的平均斜率来反映能量释放与增长的快慢,即
(1)
(2)
式中:Re为应变能释放比率;ΔEe、Δεe分别为应变能曲线峰值点与结束点之间的能量差与轴向应变差;Rk为动能增长比率,ΔEk、Δεk分别为峰值强度点处的动能与峰值动能之间的能量差及对应的轴向应变差。
探索新的冲击倾向性指标,最直接的方法就是对潜在新指标与原指标做回归分析,看是否具有较好的相关性。参照A、B和C组中数值模拟的建模与校准方法,对其余5组试样开展相对应的PFC2D数值模拟试验,并保证数值模拟获得的主要力学参数与实际试验中的力学参数差距控制在5%以内,所有煤样冲击倾向性指标与数值试验结果见表3。应变能释放比率、动能增长比率与冲击倾向性各指标的回归拟合分析如图4所示。
表3 冲击倾向性测试与数值模拟计算结果
Table 3 Results of bursting liability test and numerical simulation calculation
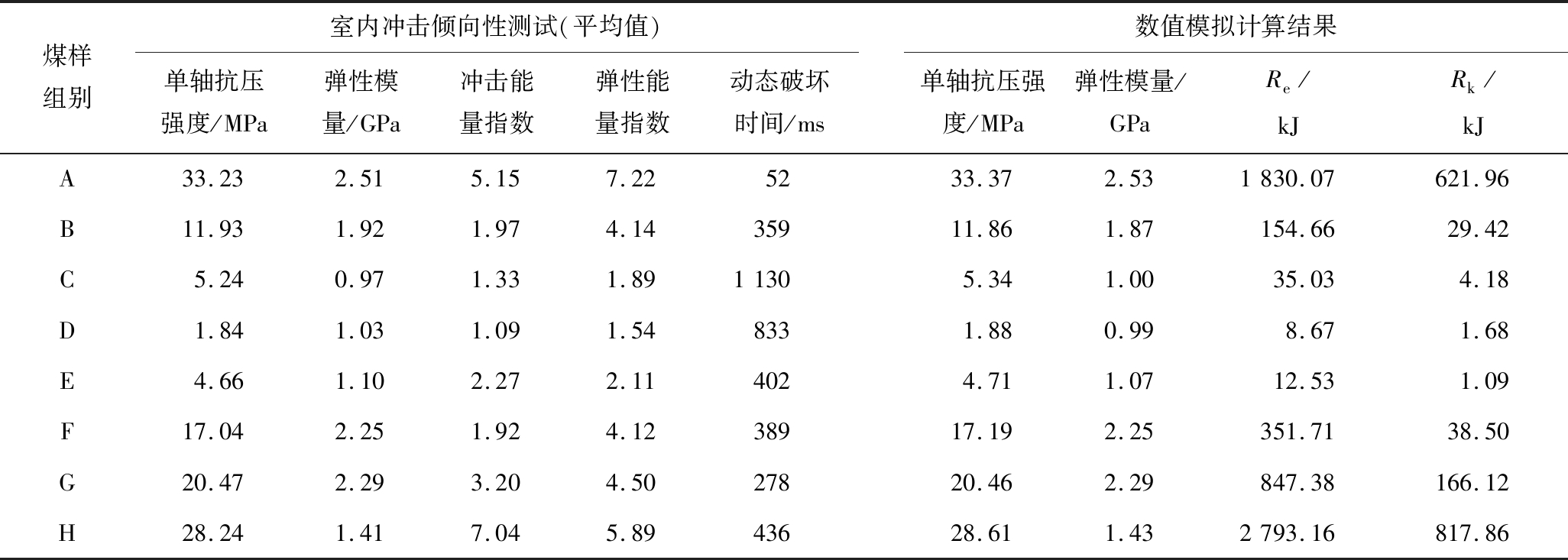
煤样组别室内冲击倾向性测试(平均值)单轴抗压强度/MPa弹性模量/GPa冲击能量指数弹性能量指数动态破坏时间/ms数值模拟计算结果单轴抗压强度/MPa弹性模量/GPaRe/kJRk/kJA33.232.515.157.225233.372.531830.07621.96B11.931.921.974.1435911.861.87154.6629.42C5.240.971.331.8911305.341.0035.034.18D1.841.031.091.548331.880.998.671.68E4.661.102.272.114024.711.0712.531.09F17.042.251.924.1238917.192.25351.7138.50G20.472.293.204.5027820.462.29847.38166.12H28.241.417.045.8943628.611.432793.16817.86

图4 应变能释放比率、动能增长比率与冲击倾向性指标相关性分析
Fig.4 Correlation between strain energy release rate,kinetic energy growth rate and indexes of bursting liability
由图4知,随着单轴抗压强度、冲击能量指数与弹性能量指数的增大,应变能释放比率和动能增长比率随之增大,呈正比例关系。应变能释放比率、动能增长比率与单轴抗压强度、冲击能量指数以及弹性能量指数之间呈现较好的相关性,尤其与冲击能量指数,相关性系数R2达0.96以上。应变能释放比率、动能增长比率与动态破坏时间的相关性较差,主要原因是动态破坏时间以毫秒为单位,其起始点与结束点拾取具有不唯一性,导致动态破坏时间的离散性很大。整体来看,应变能释放比率与动能增长比率作为评判煤的冲击倾向性具有一定的可行性,在大量室内试验与模拟数据相关性分析的基础上,可进一步研究该指标评判冲击倾向性的临界值分类标准。
3 不同冲击倾向性煤的起裂与损伤
煤岩峰前破坏过程可以分为以下4个阶段[16]:①裂纹闭合压密阶段;②线弹性变形阶段;③裂纹稳定扩展阶段;④裂纹非稳定扩展阶段。每阶段存在1个应力阈值,对应微裂纹扩展的不同阶段及特性,如图5所示,研究这些应力阈值对于从细观损伤角度研究煤岩的力学性质与破坏特征具有重要指导意义。
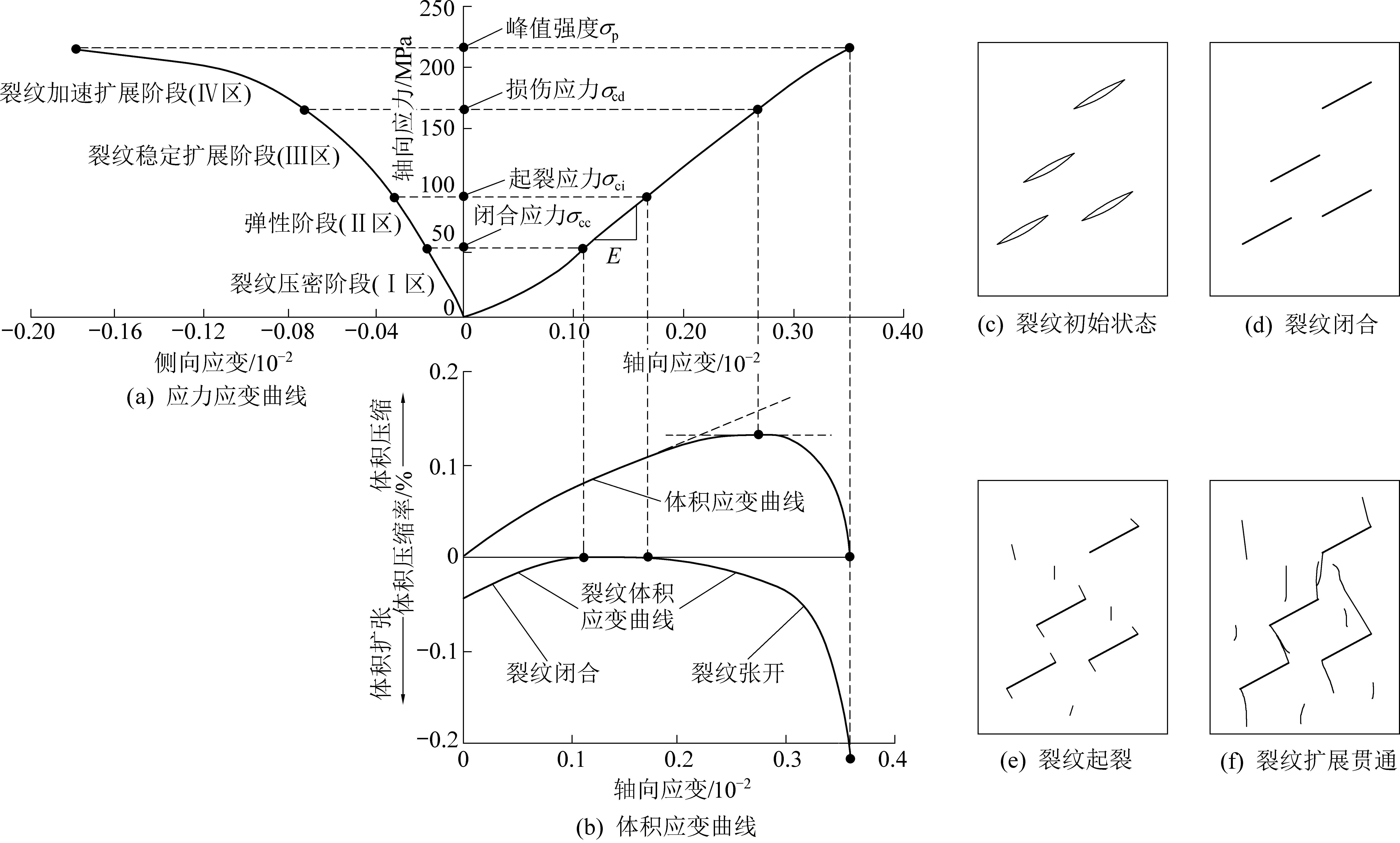
图5 煤岩破坏过程阶段划分示意[19]
Fig.5 Sketch of damage stages division of coal and rock
为查明不同冲击倾向性煤起裂与损伤的差别,笔者对不同冲击倾向性煤的起裂应力σci和裂纹损伤应力σcd进行统计分析,起裂应力对应试样内部微裂纹开始产生,试样进入裂纹稳定扩展阶段;裂纹损伤应力对应试样内部微裂纹开始贯通,试样进入裂纹非稳定扩展阶段。对于起裂应力与损伤应力,一般可通过声发射监测法和应变观察法,将裂纹萌生点对应的轴向应力作为起裂应力,而对损伤应力,一方面可取裂纹快速增长点对应的轴向应力,另一方面可取体积应变曲线弯折点所对应的轴向应力[17-19]。在颗粒流模拟中,由于能够直观记录微裂纹的发展过程,因此,笔者选取第1个微裂纹产生时对应的轴向应力作为起裂应力σci,选取体积应变曲线转折点对应的轴向应力作为裂纹损伤应力σcd,并定义起裂应力水平和损伤应力水平来反映微裂纹扩展演化特性,即
(3)
(4)
其中:Ki、Kd分别为起裂应力水平和损伤应力水平。不同冲击倾向性煤微裂纹扩展与应力应变关系曲线如图6所示,起裂应力与裂纹损伤应力阈值见表4。
由图6可知,不同冲击倾向性煤试样内部微裂纹演化规律近似,即在初始压缩较长时间内无微裂纹产生,随后微裂纹产生并经历缓慢增长和较快速增长,峰值强度点后微裂纹急剧增长,增速呈强冲击倾向性煤>弱冲击倾向性煤>无冲击倾向性煤的规律。
由图6与表4可知,基于体积应变拐点确定的损伤应力与裂纹快速增长点对应的轴向应力非常接近,验证了2种确定方法以及数据采集的准确性。不同冲击倾向性煤样的起裂应力水平在40%~60%,损伤应力水平在85%~95%,其中强冲击倾向性煤的起裂应力水平达到51.67%,损伤应力水平达到93.86%,高于弱和无冲击倾向性煤样,弱和无冲击倾向性煤样的起裂应力水平与损伤应力水平差别不大,根据煤岩起裂应力所对应的破坏阶段以及起裂应力与脆性指标的关系[21],可见强冲击倾向性煤样的弹性变形阶段更长,积累弹性应变能的能力更强,再加上其脆性更强,从而更易发生冲击性破坏。
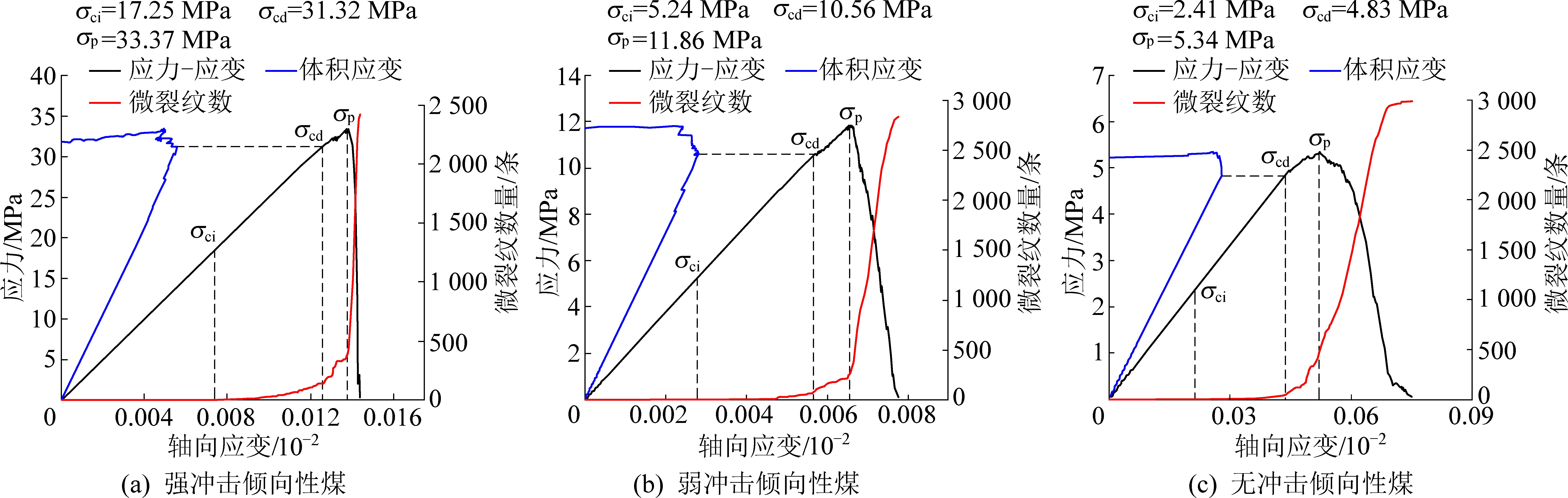
图6 不同冲击倾向性煤微裂纹扩展与应力应变关系曲线
Fig.6 Relationships between microcrack propagation and stress-strain of different bursting liability coals
表4 不同冲击倾向性煤的起裂应力水平与损伤应力水平
Table 4 Crack initiation stress and crack damage stress of different bursting liability coals

类别起裂应力水平Ki/%损伤应力水平Kd/%强冲击倾向性煤51.6793.86弱冲击倾向性煤44.1889.04无冲击倾向性煤45.1390.45
由此可见,不同冲击倾向性煤的损伤过程存在显著的差异性,峰值强度前不同冲击倾向性煤样内部微裂纹演化规律近似,均经历无微裂纹产生、微裂纹缓慢增长和较快速增长阶段;峰值强度点后微裂纹急剧增长,增速与冲击倾向性呈正相关关系。强冲击倾向性煤的起裂应力水平达到51.67%,损伤应力水平达到93.86%,高于弱和无冲击倾向性煤样,弱和无冲击倾向性煤样的起裂应力水平与损伤应力水平差别不大,起裂应力水平与损伤应力水平在一定程度上解释了强冲击倾向性煤样易积聚高弹性应变能并产生突然冲击性破坏的本质。
4 结 论
1)不同冲击倾向性煤单轴压缩下的能量演化规律相似,峰值强度前,边界能主要都转化为应变能,耗散能、滑动能与动能的占比则非常小;峰值强度后,应变能快速释放,耗散能、滑动能与动能开始迅速增长。随着冲击倾向性的增强,应变能释放与动能增长速率显著增大。
2)提出了应变能释放比率与动能增长比率的概念及表达式,应变能释放比率、动能增长比率与冲击倾向性指标中的单轴抗压强度、冲击能量指数以及弹性能量指数具有很好的相关性,可以采用这2个指标来辅助评判煤样的冲击倾向性。
3)煤的起裂应力水平主要分布在44.18%~51.67%,损伤应力水平在89.04%~93.86%。峰值强度后煤样内微裂纹剧烈增长,损伤增速与冲击倾向性呈正比。强冲击倾向性煤的起裂应力水平与损伤应力水平均高于弱和无冲击倾向性煤样;起裂应力水平与损伤应力水平反映了强冲击倾向性煤样积聚高弹性应变能并产生脆性冲击破坏的能力。
[1] 齐庆新,潘一山,李海涛,等. 煤矿深部开采煤岩动力灾害防控理论基础与关键技术[J]. 煤炭学报,2020,45(5):1567-1584.
QI Qingxin,PAN Yishan,LI Haitao,et al. Theoretical basis and key technology of prevention and control of coal-rock dynamic disasters in deep coal mining[J]. Journal of China Coal Society,2020,45(5):1567-1584.
[2] 窦林名,王云海,何学秋,等. 煤样变形破坏峰值前后电磁辐射特征研究[J]. 岩石力学与工程学报,2007,26(5):908-914. DOU Linming,WANG Yunhai,HE Xuqiu,et al. Study on electromagnetic emission characteristic for coal sample deformation and failure during pre- and post-peaking phases[J]. Chinese Journal of Rock Mechanics and Engineering,2007,26(5):908-914.
[3] 赵毅鑫,姜耀东,韩志茹. 冲击倾向性煤体破坏过程声热效应的试验研究[J]. 岩石力学与工程学报,2007,26(5):965-971. ZHAO Yixin,JIANG Yaodong,HAN Zhiru. Experimental study of acoustic and thermal infrared characteristics of bump-prone coal[J]. Chinese Journal of Rock Mechanics and Engineering,2007,26(5):965-971.
[4] 李宏艳,康立军,徐子杰,等. 不同冲击倾向煤体失稳破坏声发射先兆信息分析[J]. 煤炭学报,2014,39(2):384-388.
LI Hongyan,KANG Lijun,XU Zijie,et al. Precursor information analysis on acoustic emission of coal with different outburst proneness[J]. Journal of China Coal Society,2014,39(2):384-388.
[5] 杨 磊. 不同冲击倾向性煤体声发射能量特征与时空演化规律研究[J]. 采矿与安全工程学报,2020,37(3):101-108.
YANG Lei. Acoustic emission energy characteristics and time-space evolution law of coal with different rockburst tendency[J]. Journal of Mining & Safety Engineering,2020,37(3):101-108.
[6] 杜伟升. 冲击倾向性煤受载力学响应及能量演化特征研究[D].徐州:中国矿业大学,2018.
[7] 王 岗,潘一山,肖晓春,等. 煤体冲击倾向性指标与煤体破裂电荷关系试验研究[J]. 中国安全科学学报,2016,26(10):139-144.
WANG Gang,PAN Yishan,XIAO Xiaochun,et al. Experimental study on relationship between coal bodies burst tendency index and charge of coal bodies fracture[J]. China Safety Science Journal,2016,26(10):139-144.
[8] 张国凯,李海波,夏 祥,等. 岩石单轴压缩下能量与损伤演化规律研究[J]. 岩土力学,2015,36(S1):94-100.
ZHANG Guokai,LI Haibo,XIA Xiang,et al. Research on energy and damage evolution of rock under uniaxial compression[J]. Rock and Soil Mechanics,2015,36(S1):94-100.
[9] 丛 宇,冯夏庭,郑颖人,等. 脆性岩石宏细观破坏机制的卸荷速率影响效应研究[J]. 岩石力学与工程学报,2016,35(S2):3696-3705.
CONG Yu,FENG Xiating,ZHENG Yingren,et al. Study on effects of unloading rate on macro/meso failure mechanism of brittle rock[J]. Chinese Journal of Rock Mechanics and Engineering,2016,35(S2):3696-3705.
[10] 唐礼忠,宋徉霖. 含非共面重叠型微裂隙类岩石试样单轴受压宏细观力学特性颗粒流模拟[J]. 岩石力学与工程学报,2019,38(11):2161-2171.
TANG Lizhong,SONG Yanglin. Particle flow simulation of macro-and meso-mechanical properties of uniaxially compressed rock-like specimens with non-coplanar overlapping flaws[J]. Chinese Journal of Rock Mechanics and Engineering,2019,38(11):2161-2171.
[11] 黄彦华,杨圣奇. 非共面双裂隙红砂岩宏细观力学行为颗粒流模拟[J]. 岩石力学与工程学报,2014,33(8):1644-1653.
HUANG Yanhua,YANG Shengqi. Particle flow simulation of macro/meso/mechanical behavior of red sandstone containing two pre-existing non-coplanar fissures[J]. Chinese Journal of Rock Mechanics and Engineering,2014,33(8):1644-1653.
[12] POTYONDY D O,CUNDALL P A. A bonded-particle model for rock[J]. International Journal of Rock Mechanics and Mining Sciences,2004,41(8):1329-1364.
[13] 张社荣,孙 博,王 超,等. 双轴压缩试验下岩石裂纹扩展的离散元分析[J]. 岩石力学与工程学报,2013,32(S2):3083-3091.
ZHANG Sherong,SUN Bo,WANG Chao,et al. Discrete element analysis of crack propagation in rocks under biaxial compression[J]. Chinese Journal of Rock Mechanics and Engineering,2013,32(S2):3083-3091.
[14] ZHANG X P,WONG N Y. Cracking processes in rock-like material containing a single flaw under uniaxial compression:A numerical study based on parallel bonded-particle model approach[J]. Rock Mechanics and Rock Engineering,2012,45(5):711-737.
[15] GB/T 25217.1,煤的冲击倾向分类及指数的测定方法[S].
[16] 彭 俊,蔡 明,荣 冠,等. 裂纹闭合应力及其岩石微裂纹损伤评价[J]. 岩石力学与工程学报,2015,34(6):1091-1100.
PENG Jun,CAI Ming,RONG Guan,et al. Stresses for crack closure and its application to assessing stress-induced microcrack damage[J]. Chinese Journal of Rock Mechanics and Engineering,2015,34(6):1091-1100.
[17] 李存宝,谢和平,谢凌志. 页岩起裂应力和裂纹损伤应力的试验及理论[J]. 煤炭学报,2017,42(4):969-976.
LI Cunbao,XIE Heping,XIE Lingzhi. Experimental and theoretical study on the shale crack initiation stress and crack damage stress[J]. Journal of China Coal Society,2017,42(4):969-976.
[18] 王 宇,李 晓,武艳芳,等. 脆性岩石起裂应力水平与脆性指标关系探讨[J]. 岩石力学与工程学报,2014,33(2):264-275.
WANG Yu,LI Xiao,WU Yamfang,et al. Research on relationship between crack initiation stress level and brittleness indices for brittle rocks[J]. Chinese Journal of Rock Mechanics and Engineering,2014,33(2):264-275.
[19] 尹大伟,陈绍杰,刘兴全,等. 节理特性对花岗岩起裂应力和损伤应力影响规律颗粒流模拟[J]. 应用基础与工程科学学报,2018,26(4):808-820.
YIN Dawei,CHEN Shaojie,LIU Xingquan,et al. Particle flow simulation of effects of joint characteristics on crack initiation stress and crack damage stress of jointed granite[J]. Journal of Basic Science and Engineering,2018,26(4):808-820.
