0 引 言
页岩气等非常规油气资源作为新能源的有力补充,正日益受到重视[1]。渗透率作为影响页岩气抽采的重要参数,在页岩气抽采过程中受吸附变形、流体流态、应力应变等因素的影响。众所周知,页岩孔隙大小由纳米到毫米不等[2],不同尺度空间中气体赋存方式和传输机理存在差异。因此,研究流体流态和应力耦合作用的页岩表观渗透率变化将对页岩增透及提高采收率具有重要意义。
页岩孔隙多以纳米孔存在于有机质中,国际理论与应用化学联合会(IUPAC)按纳米孔隙尺度,将纳米孔分为微孔(孔隙直径<2 nm)、中孔(2~50 nm)和大孔(>50 nm)[3]。目前页岩气纳米孔气体传输机理的模型主要分为2种:一方面基于水动力连续性模型,修正滑脱边界条件来考虑多种传输机理[4]。CIVAN等[5]提出考虑滑脱效应的经验模型来表征气体的流动,但未考虑努森扩散。BESKOK等[6]考虑连续流动、滑脱流动、过渡流动和努森扩散建立页岩表观渗透率模型,但经验系数过多,壁面处气体流速预测值偏大。WU等[7]在Beskok的研究基础上考虑吸附气和表面扩散的影响,建立气体表观渗透率模型。ANDERSON等[8]基于连续流动模型,修正滑脱边界条件,建立页岩气复杂孔隙气体传输模型。另一方面基于多种传输机理,按一定的贡献权重系数进行叠加[4]。陈明君等[9]综合考虑页岩多尺度孔隙结构、多种气体传输机理和多种微尺度效应,建立页岩表观渗透率模型。WU等[10]分别以分子之间碰撞频率和分子与孔隙壁面碰撞频率占总碰撞频率的比值,作为滑脱流动和努森扩散的权重系数,建立页岩气复杂孔裂隙气体传输模型。李冬冬等[11]为表征实际状态下的页岩气在纳米孔隙中的运移,考虑连续流、努森扩散及表面扩散机制,推导出表观渗透率模型。WU等[12]考虑体相气体传输、表面扩散、真实气体、吸附层和应力敏感等微尺度效应的影响,建立有机质纳米孔气体传输模型。当前相关模型均未考虑应力变化的影响。
上述模型仅能描述恒定孔隙条件下的气体运移,然而动态孔隙结构的变化是由应力变化引起的。气体抽采中应力的变化将会导致孔隙结构的动态变化[13],对微孔和中孔而言,孔隙尺寸的微小变化将会改变气体流动状态。具体来说,有效应力的改变可以控制页岩的孔隙结构及孔径的大小[14]。有效应力的增加将使孔隙闭合,渗透率降低。页岩表观渗透率的变化是由有效应力、流体流态及基质收缩变形引起的。WANG等[15]考虑滑脱流动、努森扩散及气体吸附影响,建立表观渗透率模型表征气体流动。CAI等[16]考虑页岩孔隙表面的非均质性及多种传输流态的影响,建立页岩气传输三维分形介质模型。CHAI等[17]提出一种考虑多层吸附、表面扩散、真实气体效应和孔隙限域效应的单组分气体表观渗透率模型。上述相关学者对于页岩表观渗透率模型的研究通常是在不同围压条件下建立的,对于多种边界条件下的渗透率模型研究欠缺。
综上所述,相关学者主要开展关于页岩传输机理和渗流试验研究,传输模型大多未考虑动态孔隙结构的影响,试验研究主要为不同围压条件下的渗流试验,其理论多为渗透率和有效应力的经验方程形式来体现,对于考虑流体流态与应力耦合理论鲜见报道。有鉴于此,笔者力图建立按照一定贡献权重系数叠加的考虑黏性流动(滑脱流动)、努森扩散的体相气体传输模型,进一步结合应力应变关系,构建不同围压、孔隙压力2种条件下的考虑流体流态和应力耦合作用的页岩表观渗透率模型,验证其合理性,并分析页岩表观渗透率演化规律。
1 气体传输模型建立
1.1 体相气体传输模型
由于过渡流动与努森扩散、滑脱流动之间在流量计算方面存在重叠,所以当前体相气体传输模型大多是基于黏性流动、滑脱流动与努森扩散进行权重系数叠加。其中,气体平均分子自由程[18]可表示为
(1)
式中:λg为气体平均分子自由程,m;KB为玻尔兹曼常数,取1.3805×10-23 J/K;T为地层温度,K;d为分子直径,m;p为孔隙压力,MPa。
纳米孔气体对应的克努森数[18]可表示为
Kn=λg/(2r)
(2)
式中:Kn为气体对应的克努森数;r为孔隙半径,m。
1.1.1 黏性流动(滑脱流动)
当页岩孔径减小,此时孔隙壁面的分子速度不再为零,存在滑脱效应。CIVAN等[19]认为此时气体的传输流量由气体分子在孔隙壁面的滑脱流量和基于达西定律的黏性流量组成。JAVADPOUR等[20]通过一个无因次理论系数F来修正滑脱速度为
(3)
式中:R为气体常数,取8.314 J/(mol·K);M为气体摩尔质量,kg/mol;η为理想气体黏度,Pa·s;pavg为平均压力,MPa;f为气体分子随扩散与孔隙壁面碰撞的比例。
考虑气体滑脱效应的黏性流量可表示为
(4)
式中:Jvs为气体考虑滑脱效应黏性流量,kg/(m2·s);ρavg为平均密度,kg/m3;l为气体传输方向上的距离,m。
1.1.2 努森扩散
当Kn>>1,气体传输为努森扩散,此时气体分子与孔隙壁面碰撞为主,则考虑壁面粗糙度的理想气体努森扩散[12]可表示为
(5)
式中:Jk为气体努森扩散流量,kg/(m2·s);ζmb为气体在多孔介质中流动时的修正系数,ζmb=φ/τ,φ为孔隙度,τ为迂曲度;Df为分形维数;δ为分子直径与局部孔隙直径的比值。
基于REXER等[22]的液氮吸附试验数据与FHH模型来计算页岩表面分形维数[23],可用方程将其表示为
(6)
式中:V为平衡压力pb下的吸附气体体积,cm3;Va为单分子层吸附气体体积,cm3;C为常数;A为拟合直线斜率;pb0为气体饱和蒸汽压,MPa;Pb为平衡压力,MPa。
在低温条件下,页岩表面分形维数计算结果如图1所示。
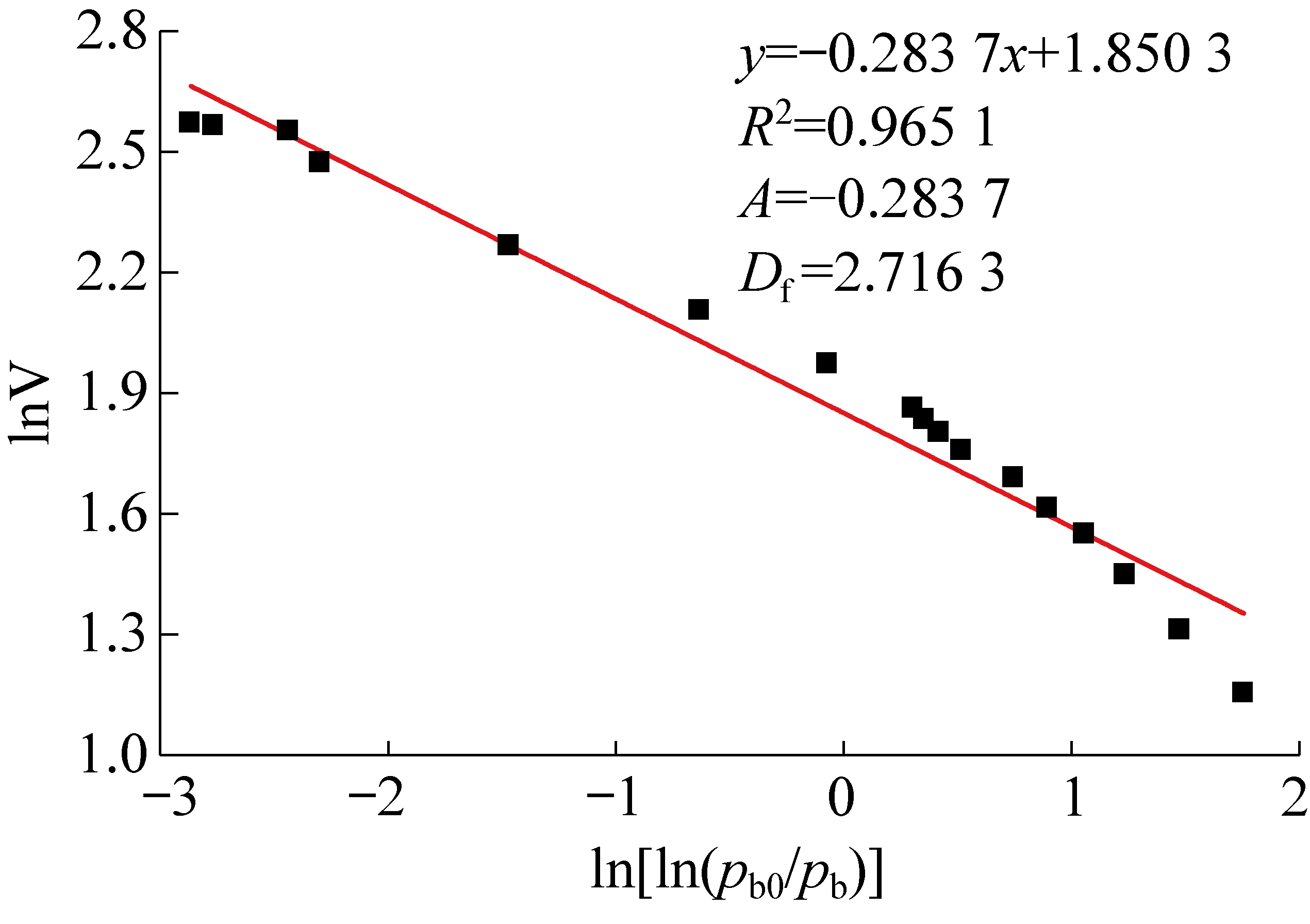
图1 页岩分形维数
Fig.1 Fractal dimension of shale
1.1.3 体相气体传输机理耦合
纳米孔体相气体总传输流量表达式为
JT=WVJvs+WKJK
(7)
且有![]()
式中:JT为纳米孔体相气体总传输流量,kg/(m2·s);WV为黏性流动(滑脱流动)权重系数;WK为努森扩散权重系数。
将式(4)和式(5)代入式(7)可得
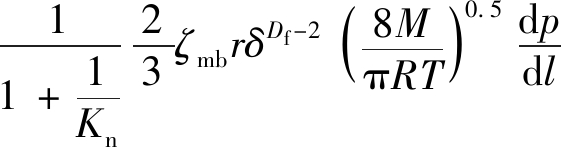
(8)
经达西定律换算,根据式(8)可推导出页岩纳米孔体相气体表观渗透率模型为
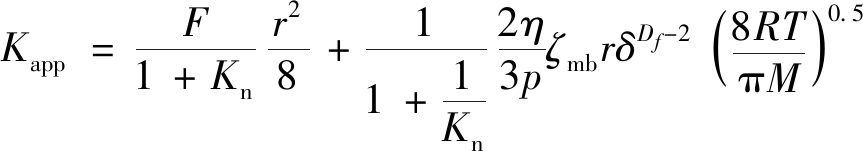
(9)
式中:Kapp为页岩表观渗透率,μm2。
1.2 考虑流体流态和应力耦合作用的页岩表观渗透率模型
上述页岩表观渗透率模型仅能够描述恒定孔隙条件下气体运移,而在真实储层环境条件下,页岩表观渗透率与应力、吸附变形及流体流态有关。因此,对于页岩表观渗透率中考虑滑脱流动的黏性流分量,采用基于应力应变关系改进的渗透率模型。
1.2.1 吸附变形
岩体变形通常受到了应力、气体压力、气体吸附解吸等因素影响,则考虑过剩吸附量的吸附变形公式为[24]
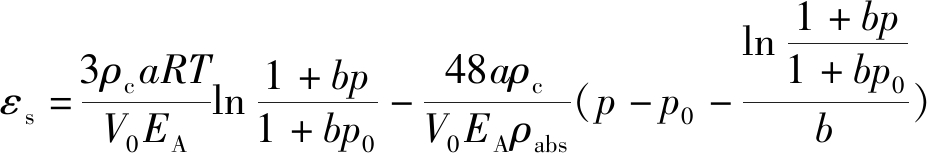
(10)
式中:εs为页岩吸附产生的体积应变;p0为初始孔隙压力,MPa;ρc为页岩密度,kg/m3;a、b为吸附常数,cm3/g、MPa-1;T为温度,K;ρabs为吸附相密度,299 kg/m3[22];V0为标准摩尔体积,约22.4×10-3 m3/mol;EA为页岩吸附所导致的膨胀模量,1900 MPa[25]。
1.2.2 修正的S&D渗透率模型
Shi-Durucan模型(S&D模型)对热收缩和基质收缩进行直接类比,可以将页岩等温解吸的应力应变关系表示为[26]
(11)
(12)
式中:~为变量;G为剪切模量,MPa;λ为页岩的第一Lame系数;![]() 为各个方向上页岩体积应变变化量之和;δij为
为各个方向上页岩体积应变变化量之和;δij为![]() 为各个方向上有效应力增量,MPa。
为各个方向上有效应力增量,MPa。
其中,围压增量![]() 由有效应力增量
由有效应力增量![]() 决定,二者之间关系可表示为[27]
决定,二者之间关系可表示为[27]
(13)
式中:![]() 为各个方向上的围压增量,MPa;α为Biot系数。
为各个方向上的围压增量,MPa;α为Biot系数。
由于剪应力分量不受热收缩和基体收缩的影响,这3种正应力分量的应力应变关系为
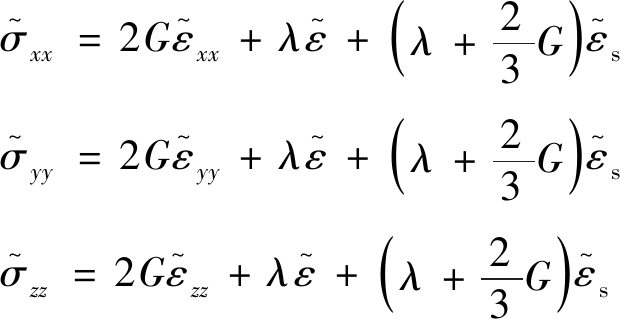
(14)
在静水平试验条件下,各个方向的应力应变关系应表示为
(15)
式(14)可以变为
(16)
基于胡克定律,并经过计算和化简可得x方向的变形量为
(17)
式中:E为弹性模量,MPa;μ为泊松比。
将式(17)代入式(16)得
(18)
由弹性力学理论可知,不同应力条件下,页岩渗透率的表达式不同。当围压不变时,式(13)为
(19)
当孔隙压力不变时,式(13)为
(20)
当围压不变时,将式(19)代入式(18)得
(21)
当孔隙压力不变时,页岩表观渗透率与吸附变形无关,则将式(20)代入式(18)得
(22)
其中G与λ可分别表示为
(23)
(24)
将式(23)、式(24)代入式(21)得
(25)
将式(23)、式(24)代入(22)得
(26)
由S&D模型可知渗透率与水平有效应力差之间存在指数函数关系[26]
k=k0exp[-3Cf(σ-σ0)]
(27)
式中:k为渗透率,10-18 m2;k0为初始渗透率10-18 m2;Cf为割理压缩系数,MPa-1。
1.2.3 不同围压条件下的页岩表观渗透率模型
将式(25)代入式(27)得不同围压条件下的渗透率模型为
(28)
式(28)说明滑脱效应与应力有关,经Klinkenberg方法校正后气测渗透率表示为[28]
k0=k∞(1+B/p)
(29)
式中:k∞为克氏渗透率,10-18 m2;B为滑脱因子。
滑脱因子B其定义为[29]
B=4cλgp/r
(30)
式中:c为比例因子,c≈1。
将式(29)代入式(28)得考虑吸附变形、滑脱效应影响的渗透率模型为
k=k∞![]()
(31)
将式(31)代入式(9),得不同围压条件下考虑流体流态和应力耦合作用的页岩表观渗透率模型为
![]()
![]()
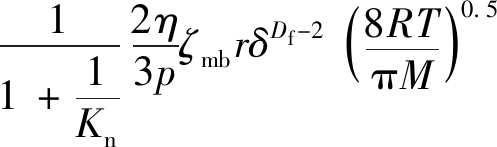
(32)
1.2.4 不同孔隙压力条件下的页岩表观渗透率模型
将式(26)代入式(27)中得不同孔隙压力条件下的渗透率模型为
(33)
将式(29)代入式(33)得到考虑滑脱效应影响的渗透率模型得
k=k∞![]()
(34)
式中:α取值为1。
将式(34)代入式(9)得到不同孔隙压力条件下的考虑流体流态和应力耦合作用的页岩表观渗透率模型为
![]()
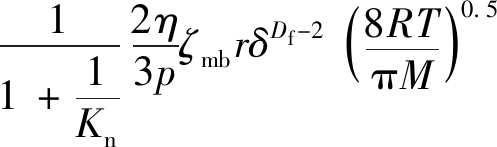
(35)
2 页岩表观渗透率模型验证
为探究在页岩气开采过程中,应力、吸附解吸、流体流态等因素变化导致的页岩表观渗透率变化规律。选择AMIN等[30]的试验数据,将模型计算结果与不同围压和不同孔隙压力2种条件下的页岩表观渗透率实测值进行对比,验证模型的可靠性。
2.1 不同围压条件下页岩表观渗透率模型验证
采用模型预测CH4测页岩表观渗透率的数据,与试验值对比,验证式(32)模型的合理性,并且计算出新建模型渗透率计算值与试验所测渗透率值的平均绝对偏差比,计算模型基本参数如下:

泊松比/μ0.3[31]页岩密度ρc/(kg·m-3)2.614×103[22]甲烷气体黏度ηCH4/(Pa·s)1.21×10-5迂曲度/τ2[31]孔隙度φ/%5[31]分子直径与局部孔隙直径的比值δ0.5[12]甲烷相对分子质量MCH4/(kg·mol-1)16×10-3温度T/K318.15[30]弹性模量E/GPa20[31]分形维数Df2.7163孔隙半径r/m2×10-9[32]氦气气体黏度ηHe/(Pa·s)2.08×10-5氦气相对分子质量MHe/(kg·mol-1)4×10-3氦气分子直径dHe/m0.26×10-9甲烷分子直径dCH4/m0.38×10-9吸附常数a/(cm3·g-1)3.648吸附常数b/MPa-10.2817
将中的相关参数代入式(32)得到不同围压条件下页岩表观渗透率与孔隙压力的关系如图2所示。
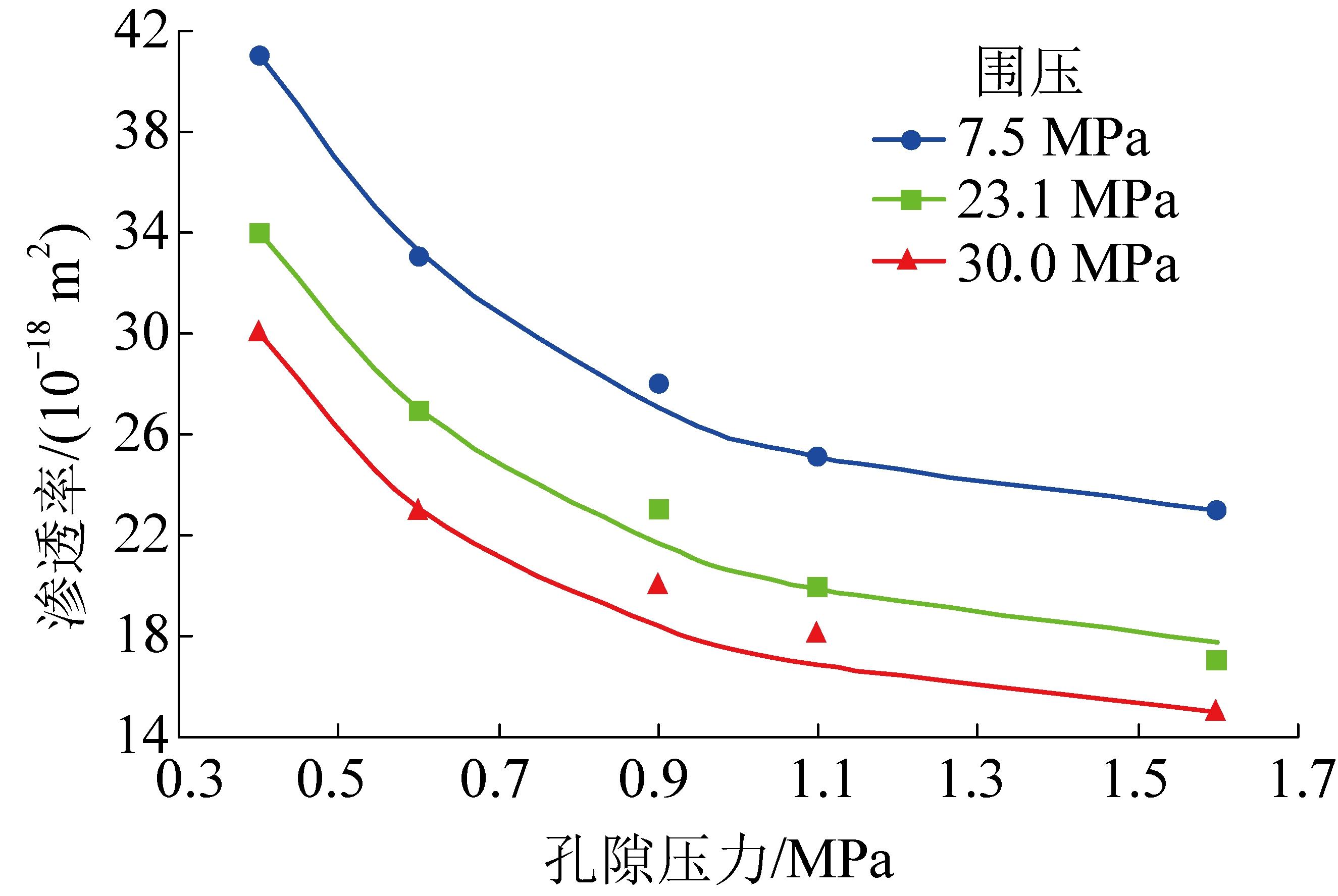
图2 不同围压条件下页岩表观渗透率与孔隙压力的关系
Fig.2 Relationship between shale apparent permeability and pore pressure under different confining pressures
计算误差公式为
(36)
式中:n为试验和拟合数据的点数;K1为试验所测数据。
在不同围压条件下根据模型计算出的曲线与试验所测的渗透率值具有良好的一致性。页岩表观渗透率随孔隙压力的升高而呈指数函数形式降低。究其原因,随孔隙压力升高,页岩逐渐被压密压实,孔隙率逐渐降低,气体渗流难度逐渐升高。同时,随孔隙压力升高,页岩吸附作用逐渐增强,使吸附变形量和页岩表面吸附层厚度均变大,进而导致气体渗流通道变窄。
此外,在孔隙压力较低时,滑脱效应也会对页岩渗透率造成影响[33]。而在孔隙压力持续升高的过程中,渗透率呈平缓的变化趋势。主要因为在此阶段页岩吸附气体逐渐趋于饱和,吸附导致孔径逐渐减小,气体传输流态主要从滑脱流态转变为努森扩散流态,滑脱效应逐渐减弱,导致渗透率变化逐渐趋于平缓。整个孔隙压力升高的过程中,孔隙压力改变引起的吸附作用决定了表观渗透率的变化。
表1 式(32)模型参数
Table 1 Model parameters(equation(32))
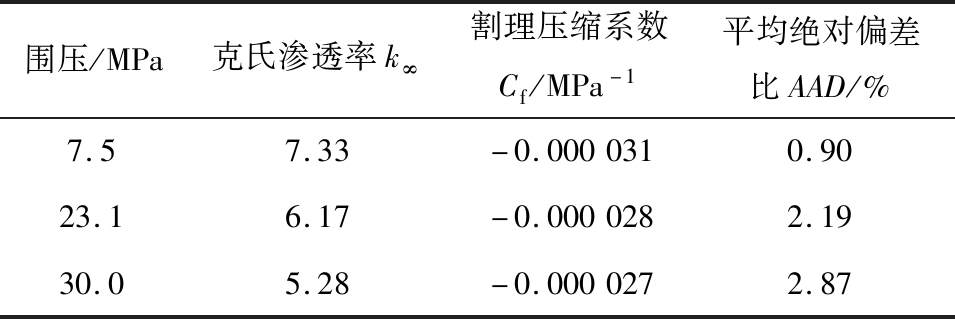
围压/MPa克氏渗透率k∞割理压缩系数Cf/MPa-1平均绝对偏差比AAD/%7.57.33-0.0000310.9023.16.17-0.0000282.1930.05.28-0.0000272.87
通过表1可以看出,新建模型与试验的渗透率值的平均绝对偏差比AAD较小,可靠性高。此外,新建模型计算的裂隙压缩系数Cf的绝对值整体呈现下降趋势。究其原因,随着围压的升高,页岩基质被压密,可压缩体积变小。因此,在较高的围压时,Cf的绝对值较小。这进一步证实了模型参数的合理性,而且变化的裂隙压缩系数更能真实的匹配模型[27]。
2.2 不同孔隙压力条件下页岩表观渗透率模型验证
将孔隙参数代入式(35)计算得到元素He测页岩表观渗透率与围压的模型曲线,并且计算出新建模型渗透率计算值与试验所测渗透率值的平均绝对偏差比AAD。图3为不同孔隙压力条件下页岩表观渗透率与围压之间的关系。
由图3可知,随围压的升高,页岩表观渗透率呈指数函数形式降低。究其原因,页岩孔隙十分发育,由于受到围压作用内部孔隙挤压变形,有效渗流通道逐渐变窄,渗透率下降[31]。此外在围压加载初期压力较低,He气体平均分子自由程与页岩孔径具有可比性,滑脱效应增强,此时滑脱效应对页岩表观渗透率的影响较大。随着围压的持续升高,孔径减小,伴随着传输流态的改变,此时气体传输流态转变为努森扩散流态,气体分子与壁面的碰撞占主导地位,滑脱效应减弱,渗透率逐渐降低。
由表3可知,新建模型与试验的渗透率值的平均绝对偏差比AAD较小,模型与实测值具有较好的一致性。此外,新建模型计算的裂隙压缩系数Cf整体呈现下降趋势。主要原因,孔隙压力升高,产生向外的膨胀应力使页岩基质压密变形,可压缩体积变小。因此,在较高的孔隙压力时,Cf较小,进一步证实了模型参数的合理性。
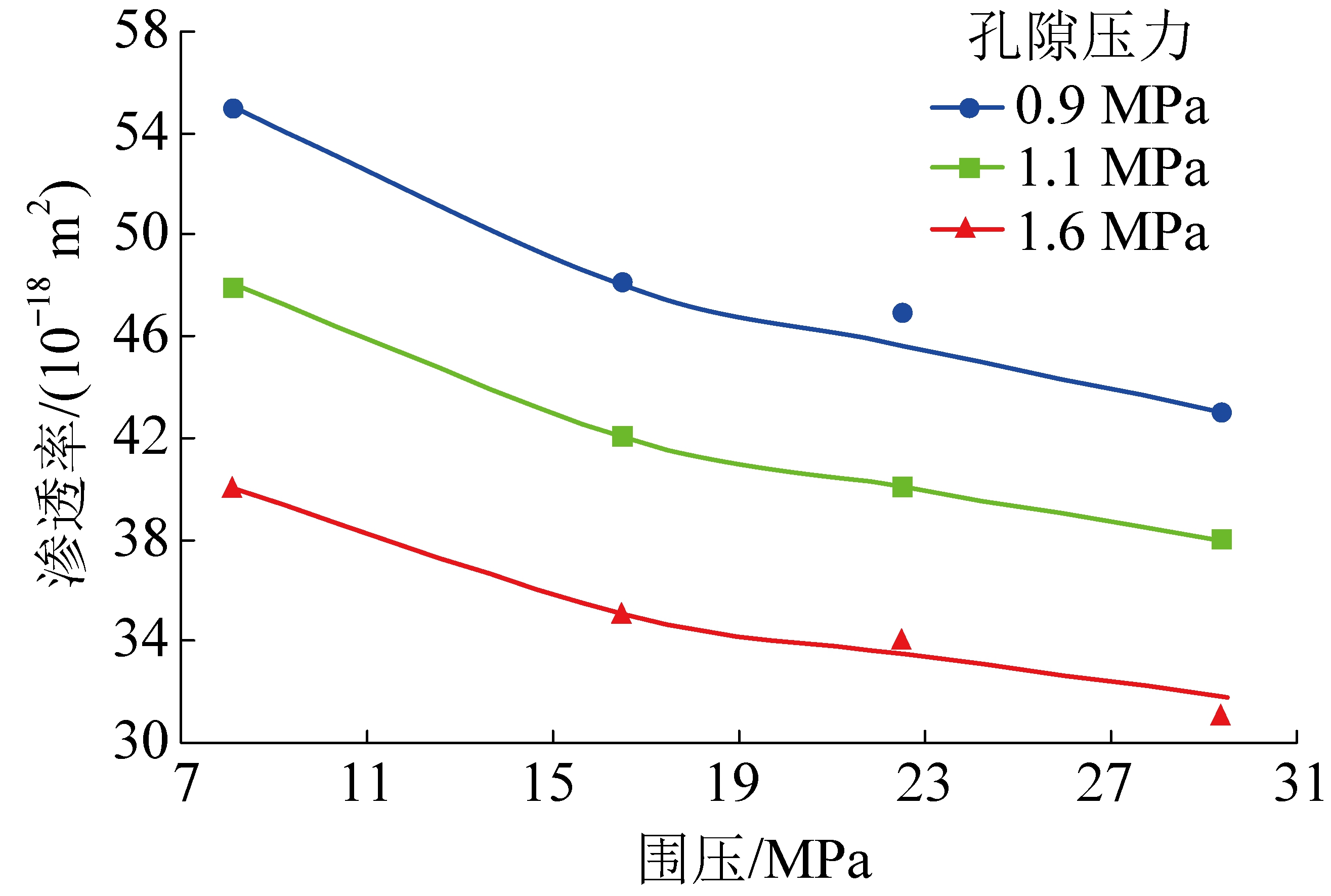
图3 不同孔隙压力条件下页岩表观渗透率与围压之间的关系
Fig.3 Relationship between shale apparent permeability and confining pressure under different pore pressures
表3 式(35)模型参数
Table 3 Model parameters(equation(35))
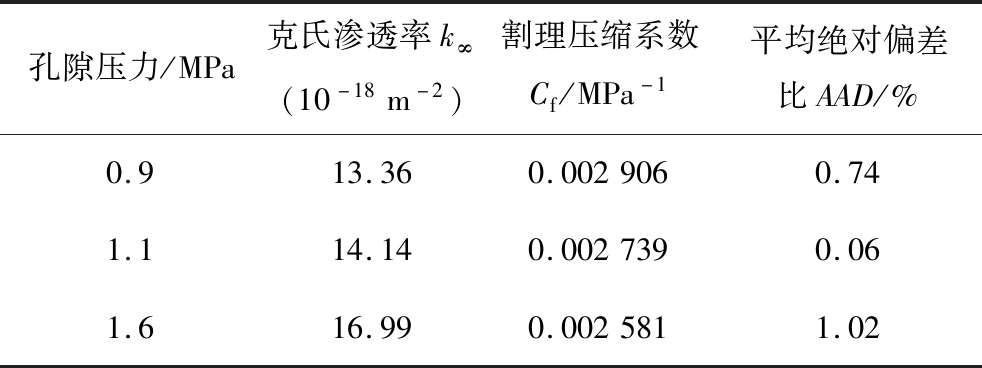
孔隙压力/MPa克氏渗透率k∞(10-18m-2)割理压缩系数Cf/MPa-1平均绝对偏差比AAD/%0.913.360.0029060.741.114.140.0027390.061.616.990.0025811.02
3 页岩表观渗透率模型影响因素分析
3.1 权重系数
根据式(1)和式(2),权重系数是孔隙压力和孔径的函数。两个权重系数的相对贡献以(Wk/Wv)的形式体现如图4所示。
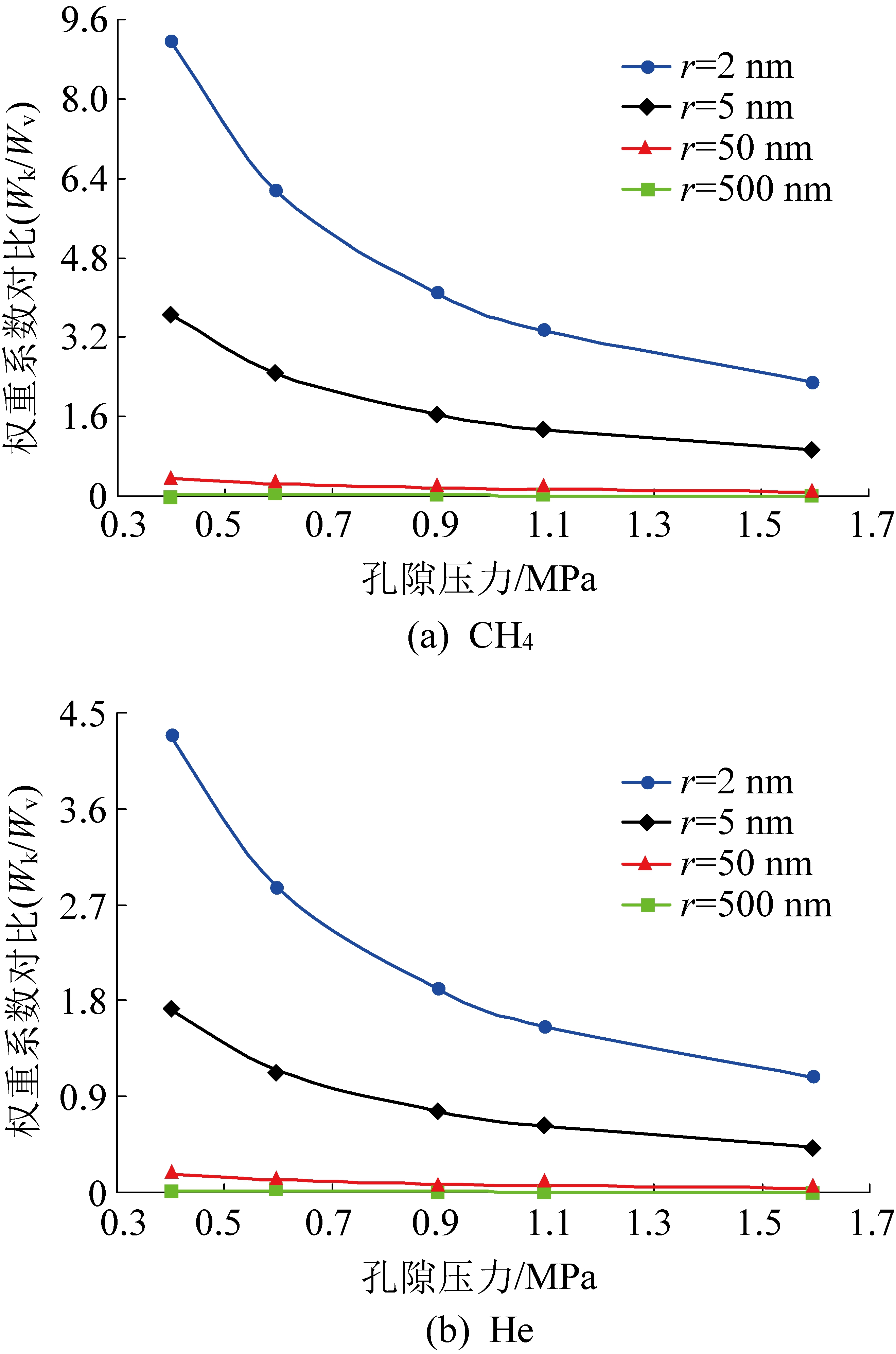
图4 不同孔径条件下贡献权重与孔隙压力关系
Fig.4 Relationship between contribution weight and pore pressure under different pore sizes
由图4可知,该比值代表努森扩散对黏性流动(滑脱流动)的贡献的百分比。当孔隙压力降低时,比值升高,说明在低压下努森扩散所占比重较大,此时气体传输流量主要由努森扩散流量贡献;同时气体流动路径越小,努森加权系数的影响越大。究其原因,在低压或小孔径的条件下,气体平均分子自由程较大,碰撞主要发生在气体分子与孔隙壁面之间,此时努森扩散对总传输流量的影响较大。
3.2 弹性模量
在恒定围压7.5 MPa条件下,根据式(32)模型,选择6个不同的弹性模量来探讨不同弹性模量条件下页岩表观渗透率与孔隙压力的关系(图5),由图5可知:弹性模量通常被用作衡量岩石产生弹性变形难易程度的指标,弹性模量增大会导致在其压力阶段内有较高的渗透率。弹性模量受到应力与应变关系的影响,在相同孔隙压力条件下,弹性模量较大的页岩基质变形量较小,且在页岩气抽采过程中,随孔隙压力降低,吸附气体解吸,此时弹性模量越大表明页岩的变形量越小,即在解吸过程中引起的基质变形量越小,页岩孔径增大量减小。因此,渗透率变化量也将随之降低。并且在低压条件下,气体扩散起主导作用,较小的流动孔径长度会引起更为明显的滑脱效应,渗透率也会相应升高。因此,表观渗透率模型对弹性模量较为敏感,且受水平方向的应变影响较大[15],且在低压条件下,页岩被压密作用减弱,孔隙率逐渐升高,渗流通道变宽,页岩表观渗透率升高。
3.3 平均孔径
由于模型引入了孔径大小作为努森渗透率分量的一个关键参数,因此在低压非达西流区域,通过改变孔径的大小来确定其对表观渗透率的影响。基于式(32)、式(35)表观渗透率模型,分别选择CH4、He两种气体在7个不同的孔径条件下探讨页岩表观渗透率与应力的关系(图6)。
由图6可知,新建模型是基于努森数来区分多种传输流态,因此在孔隙尺度减小时,流动尺度也将由宏观向微观转化。如图6a所示,当孔隙压力小于1.1 MPa时,随着孔径的减小,表观渗透率逐渐增大。究其原因,一方面页岩小孔、中孔、大孔的气体传输主控机理不同,对应的气体扩散能力也不同[3]。页岩大孔气体平均分子自由程远小于孔径,气体与孔隙壁面的碰撞频率小于气体分子之间的碰撞频率,此时气体以黏性流动为主。当页岩孔隙尺度减小,气体平均分子自由程增大,此时气体分子自由程与孔隙直径具有可比性,气体分子与孔隙壁面的碰撞不可忽略,气体发生滑脱流动,渗透率升高;另一方面,孔隙压力降低,气体解吸导致吸附厚度变小,渗透通道变大,渗透率升高。

图5 不同弹性模量条件下页岩表观渗透率与孔隙压力关系
Fig.5 Relationship between shale apparent permeability and pore pressure under different elastic modulus

图6 不同孔径条件下页岩表观渗透率与应力关系
Fig.6 Relationship between apparent permeability and stress of shale under different pore sizes
如图6b所示,围压越低渗透率越高,主要因为围压对页岩起的是向内的挤压作用,压力越小挤压作用越小,孔隙越宽,渗透率越高。且孔径越小,孔隙壁面的气体分子发生滑脱流动,此时渗透率会随着孔径的减小而增大。
3.4 滑脱效应
通过将试验数据分别代入式(28)、式(33)和式(9)计算得到未考虑滑脱效应的页岩表观渗透率,并将其与考虑滑脱效应的渗透率进行对比,分别得到围压为7.5、30.0 MPa和孔隙压力为0.9、1.6 MPa条件下的渗透率曲线对比图(图7),图7黑线为模型曲线,红线为未考虑滑脱效应曲线。

图7 考虑与不考虑滑脱效应的渗透率曲线对比
Fig.7 Comparison of permeability curves with and without slippage effect
由图7a可知,无论是否考虑滑脱效应的影响,渗透率均随孔隙压力的升高而降低。此外在围压为7.5、30 MPa时,考虑滑脱效应的渗透率计算值要比没有考虑滑脱效应的计算值更大一些,且更加吻合试验所测得的数据点。当围压为7.5 MPa,孔隙压力为0.6、0.9、1.1、1.6 MPa时,未考虑滑脱效应的页岩表观渗透率比考虑滑脱效应的渗透率分别下降了4.412 %、4.381 %、4.368 %、4.352 %,即在一定围压条件下,随着孔隙压力的升高,滑脱效应引起的渗透率变化量逐渐降低。在围压为30 MPa时,出现了与7.5 MPa同样的试验规律,这与前人的研究一致[34],究其原因,孔隙压力越大,气体分子密度越大,与页岩孔隙面碰撞概率相对也越大,气体传输流态逐渐从滑脱流态转变为努森扩散流态,滑脱效应越不明显。此外,随孔隙压力持续升高,页岩吸附层厚度逐渐增大,孔径逐渐减小,传输能力随孔径的减小而减小[4]。因此,孔隙压力是造成滑脱效应对渗透率的贡献率减小的主控因素。
由图7b可知,考虑滑脱效应页岩表观渗透率计算值均大于不考虑滑脱效应渗透率计算值,且更接近试验测量值,无论考虑滑脱效应与否,渗透率随围压升高的变化趋势一致,即逐渐降低。当孔隙压力为0.9 MPa,围压为16.4、22.5、29.4 MPa时,未考虑滑脱效应的页岩表观渗透率比考虑滑脱效应的渗透率值分别下降了2.629%、2.626%、2.622%,即在一定孔隙压力条件下,随着围压的升高,渗透率变化量逐渐降低。在孔隙压力为1.6 MPa时出现了同样的变化规律,这与前人研究一致[35]。究其原因,在围压升高过程中,使内部孔隙结构挤压变形,孔径逐渐减小,此时分子间碰撞逐渐转变为分子与孔隙壁面的碰撞,传输流态主要从滑脱流态转变为努森扩散流态,滑脱效应减弱,且传输能力随孔径的减小而减小[4],造成滑脱效应对渗透率的贡献率减小。因此,围压是造成滑脱效应对渗透率的贡献率减小的主控因素。
4 结 论
1)建立按照一定贡献权重系数叠加的考虑黏性流动(滑脱流动)、努森扩散的体相气体传输模型,利用应力应变关系同时改正渗透率模型,构建不同围压、孔隙压力2种条件下的考虑流体流态和应力耦合作用的页岩表观渗透率模型。模型可描述不同应力条件下页岩的分子动力学行为,同时还考虑了滑脱效应、孔隙结构和吸附变形对页岩表观渗透率的影响。
2)新建模型计算结果与实测值具有较好的一致性,较好的反映页岩表观渗透率与孔隙压力、围压的指数函数关系。在孔隙压力、围压持续升高的过程中,裂隙压缩系数Cf的绝对值整体呈现下降趋势,变化的Cf更能真实的匹配模型。
3)权重系数作为页岩表观渗透率模型的一个重要参数,直接影响不同传输流态的对总传输流量的贡献,CH4和He的努森扩散贡献值随孔隙压力的降低变化趋势一致,即逐渐升高;且随孔径的逐渐减小,努森扩散贡献越大。弹性模量对页岩表观渗透率影响较大,即弹性模量越大,吸附引起的基质收缩量越小,渗透率升高量降低。
4)不同孔径条件下,随围压、孔隙压力的升高,页岩表观渗透率逐渐降低;且在相同应力条件下,随流动孔径的减小,页岩主控传输机理发生改变,此时气体平均分子自由程与孔径的大小具有可比性,孔隙壁面发生滑脱流动,渗透率升高。考虑滑脱效应的渗透率计算值要比未考虑滑脱效应的值更吻合试验数据;随围压、孔隙压力的升高,滑脱效应引起的渗透率变化量逐渐降低。
[1] 张 鹏,黄宇琪,杨军伟,等.黔西北龙潭组页岩储层特征研究[J].煤炭科学技术,2019,47(4):174-180.
ZHANG Peng,HUANG Yuqi,YANG Junwei,et al.Study on characteristics of shale reservoirs from Longtan Formation in northwest Guizhou[J].Coal Science and Technology,2019,47(4):174-180.
[2] WANG Y,ZHU Y M,LIU S M,et al.Pore characterization and its impact on methane adsorption capacity for organic-rich marine shales[J].Fuel,2016,181:227-237.
[3] 吴克柳,李相方,陈掌星.页岩气纳米孔气体传输模型[J].石油学报,2015,36(7):837-848,889.
WU Keliu,LI Xiangfang,CHEN Zhangxing.A model for gas transport through nano-pores of shale gas reservoirs[J].Acta Petrolei Sinica,2015,36(7):837-848,889.
[4] 吴克柳,陈掌星.页岩气纳米孔气体传输综述[J].石油科学通报,2016,1(1):91-127.
WU Keliu,CHEN Zhangxing.Review of gas transport in nanopores in shale gas reservoirs[J].Petroleum Science Bulletin,2016,1(1):91-127.
[5] CIVAN F,RAI C S,SONDERGELD C H.Determining shale permeability to gas by simultaneous analysis of various pressure tests[J].SPE Journal,2012,17(3):717-726.
[6] BESKOK A,KARNIADAKISG E.Report:A model for flows in channels,pipes,and ducts at micro and nano scales[J].Microscale Thermophysical Engineering,1999,3(1):43-77.
[7] WU K L,LI X F,WANG C C,et al.Model for surface diffusion of adsorbed gas in nanopores of shale gas reservoirs[J].Industrial &Engineering Chemistry Research,2015,54(12):3225-3236.
[8] ANDERSON J M,MOORMAN M W,BROWN J R,et al.Isothe-rmal mass flow measurements in micro-fabricated rectangular channels over a very wide Knudsen range[J].Journal of Micromechanics and Micro-engineering,2014,24(5):1-12.
[9] 陈明君,康毅力,张廷山,等.页岩气多尺度传质特征及过程协调机制研究[J].中国科学:技术科学,2018,48(5):473-487.
CHEN Mingjun,KANG Yili,ZHANG Tingshan,et al.Characteristics of multi-scale mass transport and coordination mechanisms for shale gas[J].Scientia Sinica Technologica,2018,48(5):473-487.
[10] WU K L,LI X F,WANG CC,et al.A model for gas transport in micro-fractures of shale and tight gas reservoirs[J].Aiche Journal,2015,61(6):2079-2088.
[11] 李冬冬,张艳玉,孙晓飞,等.考虑表面扩散的实际状态页岩气表观渗透率新模型[J].中国石油大学学报(自然科学版),2018,42(4):82-90.
LI Dongdong,ZHANG Yanyu,SUN Xiaofei,et al.A new model for assessing apparent permeability of shale gas at real gas condition considering surface diffusion[J].Journal of China University of Petroleum(Edition of Natural Science),2018,42(4):82-90.
[12] WU K L,CHEN Z X,LI X F,et al.A model for multiple transport mechanisms through nano-pores of shale gas reservoirs with real gas effect-adsorption-mechanic coupling[J].International Journal of Heat and Mass Transfer,2016,93:408-426.
[13] LIU S M,HARPALANI S.Evaluation of in situ stress changes with gas depletion of coalbed methane reservoirs[J].Journal of Geophysical Research:Solid Earth,2014,119(8):6263-6276.
[14] HELLER R,VERMYLEN J,ZOBACK M.Experimental investigation of matrix permeability of gas shales[J].AAPG bulletin,2014,98(5):975-995.
[15] WANG Y,LIU S M,ZHAO Y X.Modeling of permeability for ultra-tight coal and shale matrix:a multi-mechanistic flow approach[J].Fuel,2018,232:60-70.
[16] CAI J C,LIN D L,SINGH H,et al.Shale gas transport model in 3D fractal porous media with variable pore sizes[J].Marine and Petroleum Geology,2018,98:437-447.
[17] CHAI D,YANG G,FAN Z Q,et al.Gas transport in shale matrix coupling multilayer adsorption and pore confinement effect[J].Chemical Engineering Journal,2019,370:1534-1549.
[18] GUO C H,XU J C,WU K L,et al.Study on gas flow through nano pores of shale gas reservoirs[J].Fuel,2015,143:107-117.
[19] CIVAN F,RAI C S,SONDERGELD C H.Shale-gas permeability and diffusivity inferred by improved formulation of relevant retention and transport mechanisms[J].Transport in porous media,2011,86(3):925-944.
[20] JAVADPOUR F.Nanopores and apparent permeability of gas flow in mudrocks(shales and siltstone)[J].Journal of Canadian Petroleum Technology,2009,48(8):16-21.
[21] COPPENS M O,DAMMERS A J.Effects of heterogeneity on diffusion in nanopores:from inorganic materials to protein crystals and ion channels[J].Fluid Phase Equilibria,2006,241:308-316.
[22] REXER T F,MATHIA E J,APLIN A C,et al.High-pressure methane adsorption and characterization of pores in Posidonia Shales and Isolated Kerogens[J].Energy &Fuels,2014,28(5):2886-2901.
[23] 李子文,郝志勇,庞 源,等.煤的分形维数及其对瓦斯吸附的影响[J].煤炭学报,2015,40(4):863-869.
LI Ziwen,HAO Zhiyong,PANG Yuan,et al.Fractal dimensions of coal and their influence on methane adsorption[J].Journal of China Coal Society,2015,40(4):863-869.
[24] 李波波,杨 康,李建华,等.力热耦合作用下煤岩吸附及渗透特性的试验研究[J].煤炭学报,2018,43(10):2857-2865.
LI Bobo,YANG Kang,LI Jianhua,et al.Experimental study on the adsorption and permeability characteristics of coal under the coupling stress and temperature[J].Journal of China Coal Society,2018,43(10):2857-2865.
[25] LIU S M,HARPALANI S.A new theoretical approach to model sorption-induced coal shrinkage or swelling[J].AAPG Bulletin,2013,97(7):1033-1049.
[26] SHI J Q,DURUCAN S.Drawdown induced changes in permeability of coalbeds:a new interpretation of the reservoir response to primary recovery[J].Transport in Porous Media,2004,56(1):1-16.
[27] LIU S M,HARPALANI S,PILLALAMARRY M,et al.Laboratory measurement and modeling of coal permeability with continued methane production:Part 2-modeling results[J].Fuel,2012,94:117-124.
[28] WU Y T,PAN Z J,ZAHNG D Y,et al.Experimental study of permeability behavior for prop pant supported coal fracture[J].Journal of Natural Gas Science and Engineering,2018,51:18-26.
[29] ZIARANI A S,AGUILERA R.Knudsen’s permeability correction for tight porous media[J].Transport in Porous Media,2012,91(1):239-260.
[30] GHANIZADEH A,AMANN-HILDENBRAND A,GASPARIK M,et al.Experimental study of fluid transport processes in the matrix system of the European organic-rich shales:II:Posidonia Shale(Lower Toarcian,northern Germany)[J].International Journal of Coal Geology,2014,123:20-33.
[31] 曲鸿雁,彭 岩,刘继山,等.气体吸附对页岩裂缝表观渗透率和页岩气采收率的影响[J].中国科学:技术科学,2018,48(8):891-900.
QU Hongyan,PENG Yan,LIU Jishan,et al.Impact of gas adsorption on apparent permeability of shale fracture and shale gas recovery rate[J].Science China:Scientia Sinica Technologica,2018,48(8):891-900.
[32] KLAVER J,DESBOIS G,LITTKE R,et al.BIB-SEM pore characterization of mature and post mature Posidonia Shale samples from the Hils area,Germany[J].International Journal of Coal Geology,2016,158:78-89.
[33] ZHOU Y B,LI Z H,YANG Y L,et al.Evolution of coal permeability with cleat deformation and variable Klinkenberg Effect[J].Transport in Porous Media,2016,115(1):153-167.
[34] 朱光亚,刘先贵,李树铁,等.低渗气藏气体渗流滑脱效应影响研究[J].天然气工业,2007,27(5):44-47.
ZHU Guangya,LIU Xiangui,LI Shutie,et al.A study of slippage effect of gas percolation in low permeability gas pools[J].Natural Gas Industry,2007,27(5):44-47.
[35] 左宇军,孙文吉斌,邬忠虎,等.渗透压-应力耦合作用下页岩渗透性试验[J].岩土力学,2018,39(9):3253-3260.
ZUO Yujun,SUNWEN Jibin,WU Zhonghu,et al.Experiment on permeability of shale under osmotic pressure and stress coupling[J].Rock and Soil Mechanics,2018,39(9):3253-3260.
