0 前 言
地孔瞬变电磁法探测是一种将发射回线置于地面,于钻孔中接收信号的瞬变电磁探测方法[1-2],通过研究一次场激发条件下,地下异常体产生的异常场,从而实现对孔旁异常体的探测。由于接收探头置于钻孔之中,更接近地下异常体,可获得比地面方法[3-4]更强的异常响应信号,且探头在井中受导电覆盖层和外部电磁干扰更小,使地孔瞬变电磁法在深部找矿及利用钻孔寻找孔旁、孔底盲矿等方面,具有不可替代的优势。煤矿井下开采过程中,前方隐伏地质异常体严重威胁安全生产,地孔瞬变电磁法以其特有优势,为隐伏地质异常体探测提供了新思路[5-6]。
国外开始地孔瞬变电磁法的研究时间较早,WOODS[7]通过物理模型试验,总结了地孔瞬变电磁三分量的特征关系,为地孔瞬变电磁法探测提供了理论基础。BARNETT[8]提出自由空间中良导体感应的二次场可以用一组电流环来等效,即等效电流环理论。DUNCAN[9]以等效电流环理论为基础,实现了地孔瞬变电磁磁感应强度三分量数据的电流环反演,获得了异常体的位置、产状、规模等参数。FULLARGAR[10]同样提出了采用等效电流环代替简单模型的孔中瞬变电磁反演方法。该方法在加拿大、澳大利亚等国家已被广泛应用,取得了很多非常成功的深部探矿实例[11-14]。
国内最早开展地孔瞬变电磁法技术研究的是地科院物化探研究所。1987年,胡平、吴凤翔开展了基于自由空间的球体和板状体的地孔瞬变电磁理论响应计算,绘制了大量的井中轴向分量响应曲线并成册。1990年,蒋邦远和石中英研制井中探头,并投入实际应用,随后诸多学者开展了相关研究[15-18]。近年来,该方法的研究热度不断升温。孟庆鑫等[19]采用时域有限差分法(FDTD)计算了低阻板状导体在均质半空间和有低阻覆盖层影响情况下的地孔瞬变电磁异常响应,研究分析响应的特征及规律。杨毅等[20]采用遗传算法实现了基于等效涡流理论的地孔瞬变电磁纯异常场反演。李建慧等[21]实现了基于矢量有限单元法的地孔瞬变电磁法三维正演,通过对低阻块状体地电模型的正演计算,分析总结了矩形回线源激发条件下,瞬变电磁场随时间和深度变化的扩散规律。徐正玉等[22]采用时域有限差分法模拟了三维均匀空间中垂直接触带的响应特征,总结了不同触面埋深及电阻率变化条件下的地孔瞬变电磁响应特征,为寻找深部地质结构、判断断层位置以及铀矿成矿环境等地质问题提供了理论依据。李凯等[23]采用三维多尺度时域有限差分法对矿井主要面临的顶底板层状含水体、充水陷落柱、充水断层地质灾害进行了数值试验,分析不同模型的响应特征,证明了地孔瞬变电磁法具备探测矿井不同形态含水体的能力。姚伟华等[24-25]对均匀半空间含孤立异常体模型以及异常体位于水平钻孔不同方位的地孔瞬变电磁三分量的总场和异常场响应特征进行了系统研究,利用异常场三分量反演异常体的位置、倾角和规模等参数并应用于煤矿积水采空区探测,证明了该方法可作为煤矿钻孔中探查积水采空区的有效手段。张杰等[26-27]提出了地孔瞬变电磁的矢量交会解释方法,根据异常场矢量具有指向异常体中心的特点,可以大致确定异常体的中心位置。
为了准确定位异常体的中心位置,笔者在前人研究的基础上,通过分析圆形载流回线磁场的空间分布特征,根据“等效涡流”理论,将异常场等效为电流环,提出了针对水平钻孔的地孔瞬变电磁浮动系数矢量交会算法,以磁感应强度水平分量Bx、By与垂直分量Bz的特征关系作为参考,通过构建系数库修正磁感应强度垂直分量Bz,实现合成矢量准确指向异常体中心从而定位异常体的目的。最后,通过理论模型和物理试验验证了方法的有效性。
1 方法原理
1.1 等效涡流
假设均匀一次场中存在高电导的薄板,当激励回线中的一次场瞬间消失时,由法拉第定律可知,高导薄板为了维持内部磁场,薄板内部将立即出现感应涡流,根据1998年蒋邦远[1]的研究,导电薄板产生的感应涡流,其磁矩的方向总是垂直于薄板。1984年BARNETT[8]的研究显示,感应涡流会以电流环的形式在薄板内分布,形状与薄板相似,在早期集中于板的边缘,随着时间的推移,逐渐向薄板中心扩散,一段时间后,电流分布达到平衡,随后以简单的振幅形式衰减。根据BARNETT理论和数值模拟的结果,不仅在晚期,即使在较早期,也可以用等效电流环近似表示电流的分布,如图1所示。
在地孔瞬变电磁法探测中,固定发射回线位置,激发的一次场与低阻异常体耦合关系保持不变,若钻孔附近存在低阻异常体,将在异常体内产生感应涡流,感应涡流可以等效成电流环,通过分析电流环的空间磁场分布特征及规律,计算电流环的大小、位置等参数,进而实现对异常体的空间定位,这就是等效涡流理论,此理论是地孔瞬变电磁探测中异常场分析的理论基础。

图1 导电薄板涡旋电流分布示意
Fig.1 Scroll current distribution diagram of conductive thin plate
1.2 圆形载流回线(电流环)的磁场
自由空间中建立如下的坐标系,图2中定义垂直向上Z为正,圆形载流回线的中心点为坐标原点O,其半径为R,载入电流为I,其中计算点P坐标为P(x,y,z)、P(ρ,φ,z)和P(r′,θ,φ)。其中,θ为P与Z轴的夹角,φ、φ′为电流源![]() 及点P与X轴的夹角。
及点P与X轴的夹角。
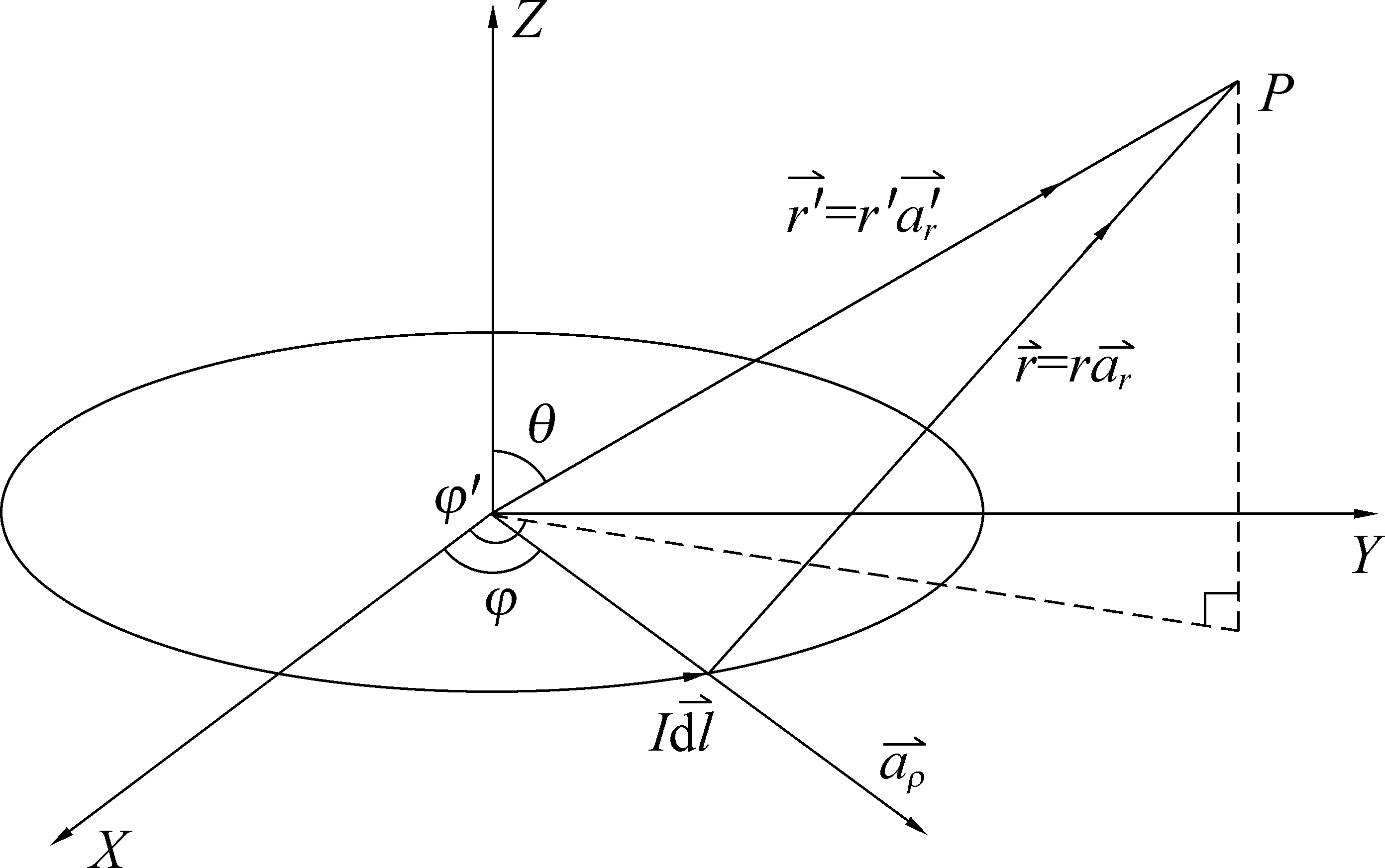
图2 圆形电流环空间任意一点的磁场
Fig.2 Magnetic field at any point in space of circular current
对于空间内任意点的磁场三分量响应可由毕奥-萨伐尔定律计算,即
(1)
式中:![]() 为电流元;
为电流元;![]() 为电流元到计算点P的矢量;μ0为介电常数。
为电流元到计算点P的矢量;μ0为介电常数。
计算点P处的磁通量密度微分的表达式为
(2)
根据坐标转换,球坐标系、柱坐标系到笛卡尔坐标系转换后各单位矢量的计算式为
(3)
式中:![]() 为单位矢量;
为单位矢量;![]() 为球坐标系单位矢量;
为球坐标系单位矢量;![]() 为柱坐标系的单位矢量;
为柱坐标系的单位矢量;![]() 为笛卡尔坐标系的单位矢量。
为笛卡尔坐标系的单位矢量。
将式(3)代入式(2)展开,即可获得圆形电流环磁感应强度Bx、By、Bz三分量的表达式为
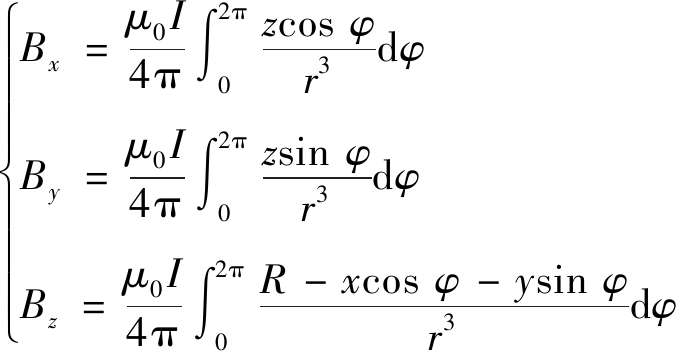
(4)
且有,![]()
假设圆形电流环中心坐标为X=0 m,Y=0 m,Z=40 m,半径为10 m,供以1 A的逆时针电流,计算电流环XY平面的磁场矢量分布(图3)。

图3 Z=40 m时XY平面磁场分布及不同孔位磁感应强度曲线
Fig.3 Distribution of magnetic field in XY plane and magnetic induction in different hole positions at Z=40 m
图中A、B、C、D、E、F分别表示6个水平钻孔的位置,红色曲线为磁感应强度Bx,蓝色曲线为磁感应强度By。由图3看出,圆形电流环磁场XY平面分布关于电流环中心对称。X<0时,磁感应强度Bx为正,X>0时为负,整体表现为S型的特征,电流环中心点,幅值为零。磁感应强度By为典型的单峰异常,电流环中心点幅值最大,远离电流环中心,幅值逐渐减小。水平孔A中磁感应强度Bx、By的幅值均比B、C孔更大,即远离电流环中心,幅值响应逐渐变小。D、E、F孔中磁感应强度Bx、By特征与A、B、C孔相同,但磁感应强度By幅值相反。
计算圆形电流环不同Y偏离距离下XZ平面的磁场矢量分布如图4所示。图中3个水平钻孔编号为A、B、C,红色曲线为磁感应强度Bx,紫色曲线为磁感应强度Bz。从图4可知,电流环XZ平面磁场矢量关于X=0轴对称,当Y方向距离不断增加时,电流环沿Z方向双向扩散,显示2个矢量汇集的中心。其中磁感应强度Bx特征与XY平面显示一致。磁感应强度Bz为单峰特征,电流环中心点幅值最强,远离电流环中心,异常幅值逐渐减小,随着偏移Y方向距离的增加,当钻孔从2个矢量汇集中心穿过时,磁感应强度Bz的形态发生反转。
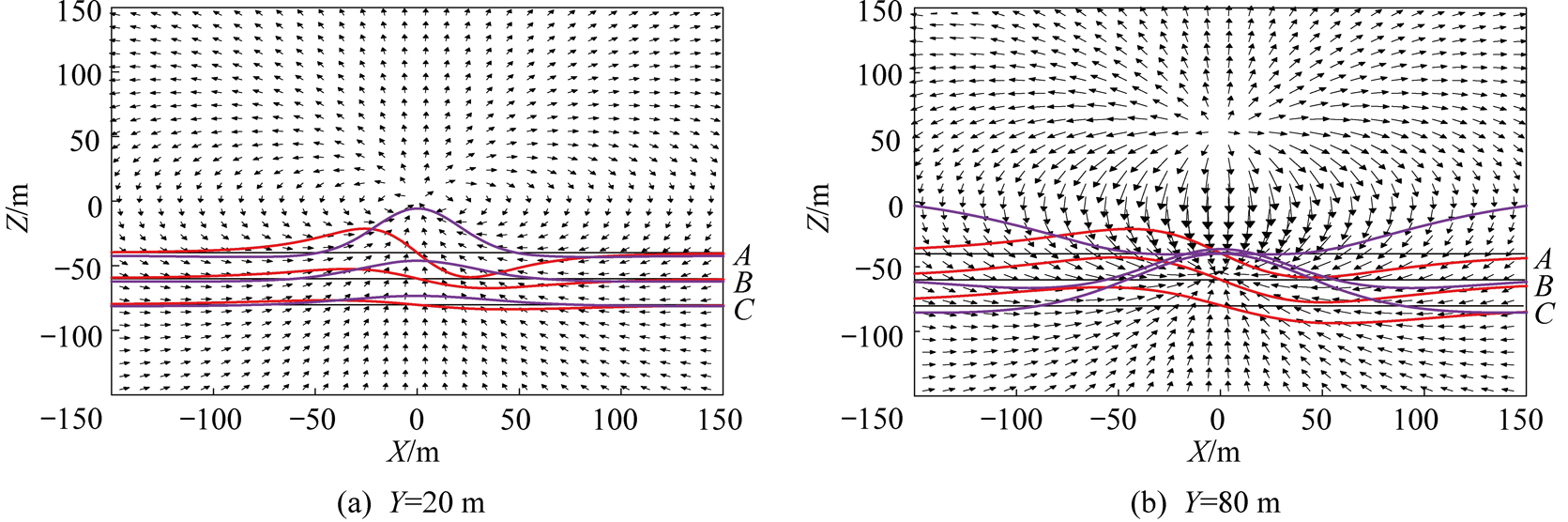
图4 不同Y方向距离时XZ平面磁场分布及不同孔位磁感应强度曲线
Fig.4 Distribution of magnetic field in plane XZ and of magnetic induction in different hole positions at different Y-direction distances
1.3 浮动系数矢量交会
根据水平电流环的磁场矢量分布(图3、图4),其辐射的磁场在XY和XZ平面上具有明显的指向性。对XY平面,尽管水平钻孔的位置发生了改变,但磁感应强度Bx与By的合成矢量均指向电流环的中心,因此可以利用合成矢量的方法确定电流环在XY平面的坐标。对XZ平面,随着钻孔沿Y方向的偏移,使得磁感应强度Bx与By的合成矢量不完全指向电流环的中心,但合成矢量汇集于电流环中心附近。这就是矢量交会的基本原理。
假设给定电流环中心坐标为X=100 m,Y=50 m,Z=-20 m,钻孔沿X轴水平放置,长度200 m,计算磁感应强度三分量响应,对磁感应强度Bx、By进行矢量合成,得到合成矢量Bxy,其矢量交会的结果如图5a)所示,合成的矢量的交会点显示电流环中心坐标为X=100 m,Y=50 m,与电流环中心点X、Y坐标一致。磁感应强度Bx、Bz的合成矢量Bxz的矢量交会结果如图5b所示,显示电流环中心坐标为X=100 m,Z=-8 m,与实际的电流环中心点Z坐标不一致。

图5 直接矢量交会结果
Fig.5 Results of direct vector intersection
通过简单的矢量合成并在相应平面进行交会,可以获得异常体中心位置的部分信息,但XZ平面交会的结果存在误差。提出一种浮动系数矢量交会算法,根据磁感应强度Bx存在明显的特征点,即中心点位置幅值为零,选取特征点处磁感应强度By的绝对值与Bz比值(ABS(By)/Bz)作为参考值,在此基础上采用不同的调节系数对磁感应强度Bz的幅值进行修正,直到合成矢量Bxz交会准确显示电流环中心位置,保留此调节系数,并形成系数库,当钻孔位于Bxz矢量汇集中心时,磁感应强度Bz出现负值,因此计算的ABS(By)/Bz参考值同样存在正负。实际应用中,首先计算出特征点处ABS(By)/Bz的比值,参考系数库插值获得磁感应强度Bz的调节系数,调节后形成新的合成矢量Bxz,再进行矢量交会,从而确定电流环中心在XZ平面的坐标。计算的部分ABS(By)/Bz调节系数见表1、表2。对前述中心点坐标X=100 m,Y=50 m,Z=-20 m电流环进行浮动系数矢量交会,特征点X=100 m处ABS(By)/Bz为2.762 5,对应调节系数为2.75。矢量交会的结果如图6c、图6d所示,结果显示利用调节系数对磁感应强度Bz调整后再矢量交会,交会结果准确指向电流环的中心位置。
表1 ABS(By)/Bz为正时磁感应强度Bz的调节系数
Table 1 Adjustment coefficient of Bz when ABS(By)/Bz is positive
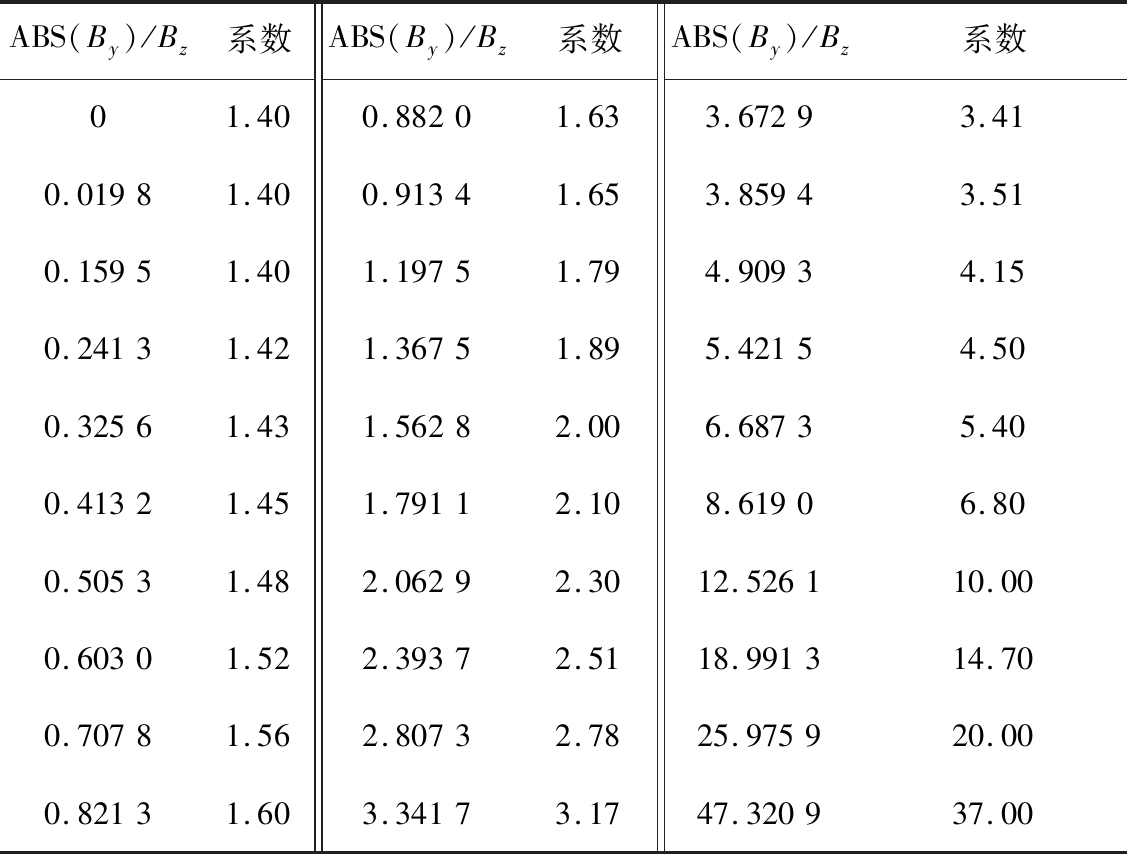
ABS(By)/Bz系数ABS(By)/Bz系数ABS(By)/Bz系数01.400.88201.633.67293.410.01981.400.91341.653.85943.510.15951.401.19751.794.90934.150.24131.421.36751.895.42154.500.32561.431.56282.006.68735.400.41321.451.79112.108.61906.800.50531.482.06292.3012.526110.000.60301.522.39372.5118.991314.700.70781.562.80732.7825.975920.000.82131.603.34173.1747.320937.00
表2 ABS(By)/Bz为负时磁感应强度Bz的调节系数表
Table 2 Adjustment coefficient of Bz when ABS (By)/Bz is negative
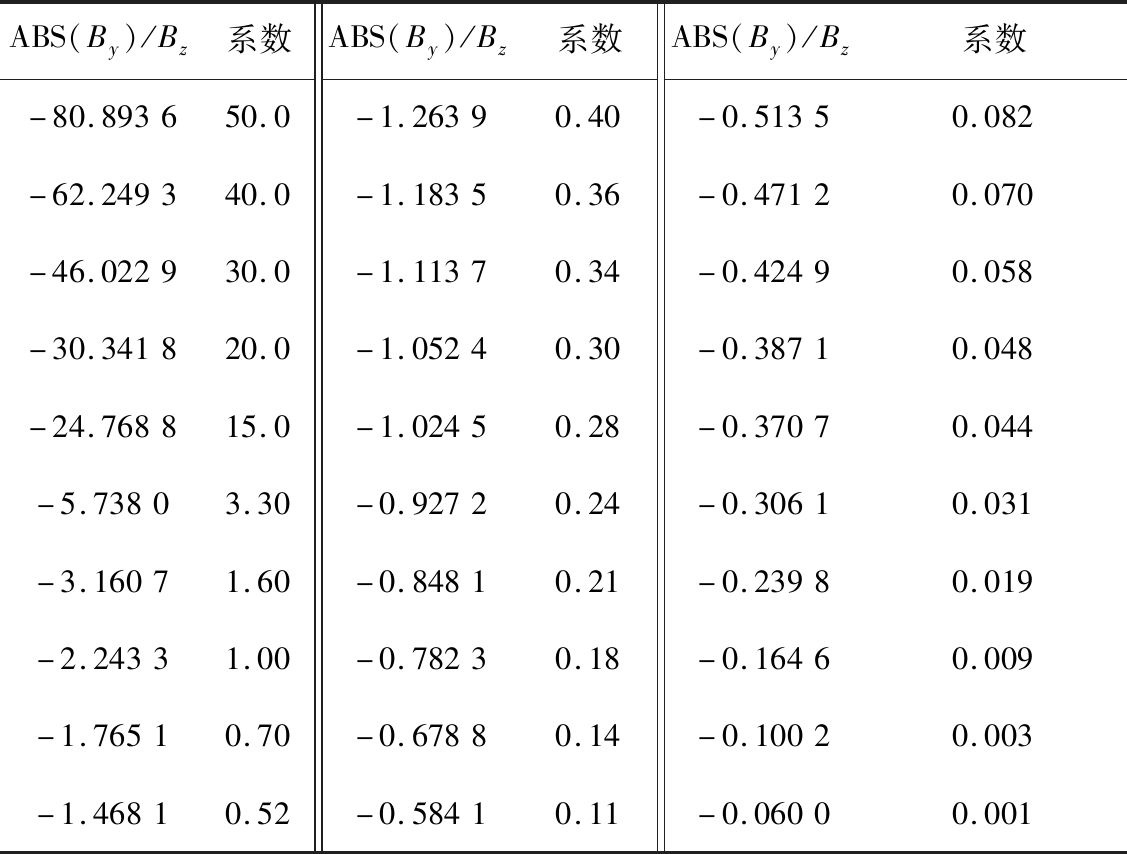
ABS(By)/Bz系数ABS(By)/Bz系数ABS(By)/Bz系数-80.893650.0-1.26390.40-0.51350.082-62.249340.0-1.18350.36-0.47120.070-46.022930.0-1.11370.34-0.42490.058-30.341820.0-1.05240.30-0.38710.048-24.768815.0-1.02450.28-0.37070.044-5.73803.30-0.92720.24-0.30610.031-3.16071.60-0.84810.21-0.23980.019-2.24331.00-0.78230.18-0.16460.009-1.76510.70-0.67880.14-0.10020.003-1.46810.52-0.58410.11-0.06000.001
2 模型验证
利用三维时域有限差分算法正演计算异常体磁感应强度三分量响应,将计算的含异常体的磁感应强度三分量响应减去相同背景均匀全空间的磁感应强度三分量响应,获得异常场磁感应强度三分量响应。设置发射回线尺寸为600 m×600 m,电流1 A,均匀半空间电阻率为100 Ω·m,水平钻孔的测线位于地下300 m,测线长200 m。添加如图7所示的异常体,异常体规模为20 m×20 m×20 m,电阻率为0.1 Ω·m,异常体中心坐标为X=78 m,Y=-24 m,Z=-34 m。
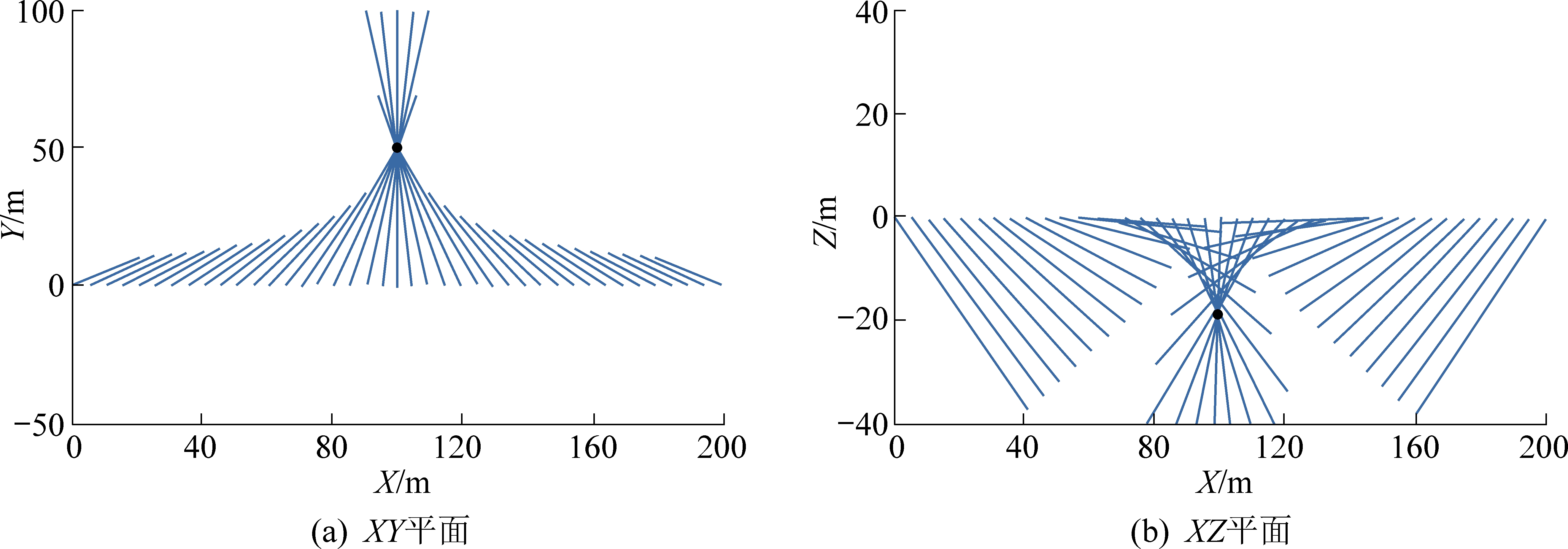
图6 浮动系数矢量交会结果
Fig.6 Results of floating coefficient vector intersection

图7 异常体相对位置示意
Fig.7 Schematic of relative position of anomalous body
经计算,异常场磁感应强度三分量响应在t=0.351 ms 时,幅值最大,磁感应强度三分量Bx、By、Bz的曲线如图8所示,曲线形态与电流环磁感应强度三分量曲线特征基本一致,因此可进行浮动系数矢量交会,矢量交会结果如图9所示。由图9可见,XY平面矢量交会的中心准确对应异常体的X、Y坐标(图9a、图9c),即为X=78 m,Y=-24 m。XZ平面直接矢量交会的结果如图9b所示,交会点显示异常体中心Z坐标约为-17 m,与实际位置相比存在偏差。利用浮动系数矢量交会计算,结果(图9d)显示异常体的中心Z坐标约为-34 m,与异常体中心位置吻合。特征点处ABS(By)/Bz为1.311 9,对应的调节系数为1.86。
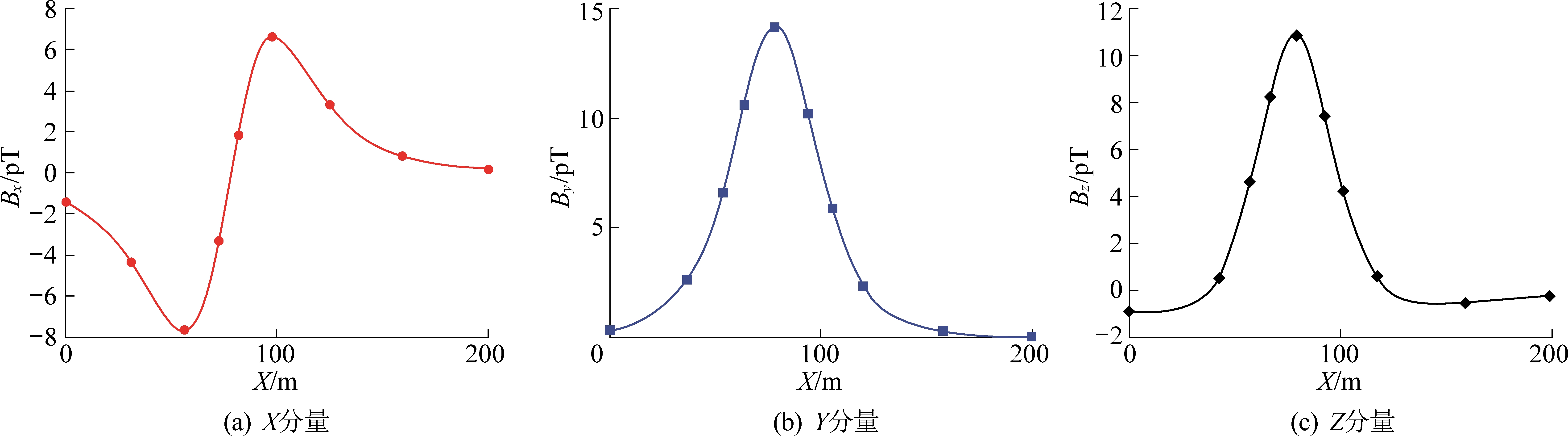
图8 磁场三分量曲线图
Fig.8 3-Component curves of magnetic field

图9 矢量交会结果
Fig.9 Result of vector intersection
3 物理模拟

图10 试验现场布置
Fig.10 Layout of test site
在野外进行物理模拟试验,试验区无明显电磁干扰,地形平坦,最大落差不超过5 m。试验参数为发射回线边长60 m×60 m、发射基频5 Hz、发射电流13 A,电流逆时针方向。人工布设7 m×5 m的金属铁板异常,水平置于坑底,距地面垂直埋深约5 m。布置测线距铁板中心约5.3 m。测点距1 m,测线长41 m。试验现场布置如图10所示。沿测线逐点测量,获得磁感应强度三分量响应,随后去掉金属薄板,再次测量,获得背景场,2次测量数据相减得到异常场磁感应强度三分量响应,t=0.366 ms时,异常响应最大,磁感应强度三分量Bx、By、Bz的曲线如图11所示。
对异常场磁感应强度三分量数据进行矢量交会,从矢量交会的结果可以看出,未对磁感应强度Bz进行调节,直接矢量交会,XZ平面矢量交会结果存在明显误差(图12b)。经浮动系数修正后,矢量交会可以较为准确的定位异常体的中心位置,图12c、图12d)显示异常体中心位置坐标大致为X=18 m,Y=6 m,Z=-5.2 m,与实际布置的模型基本一致。特征点处ABS(By)/Bz值为2.851 2,对应的调节系数为2.81。

图11 磁场三分量曲线
Fig.11 3-Component curves of magnetic field
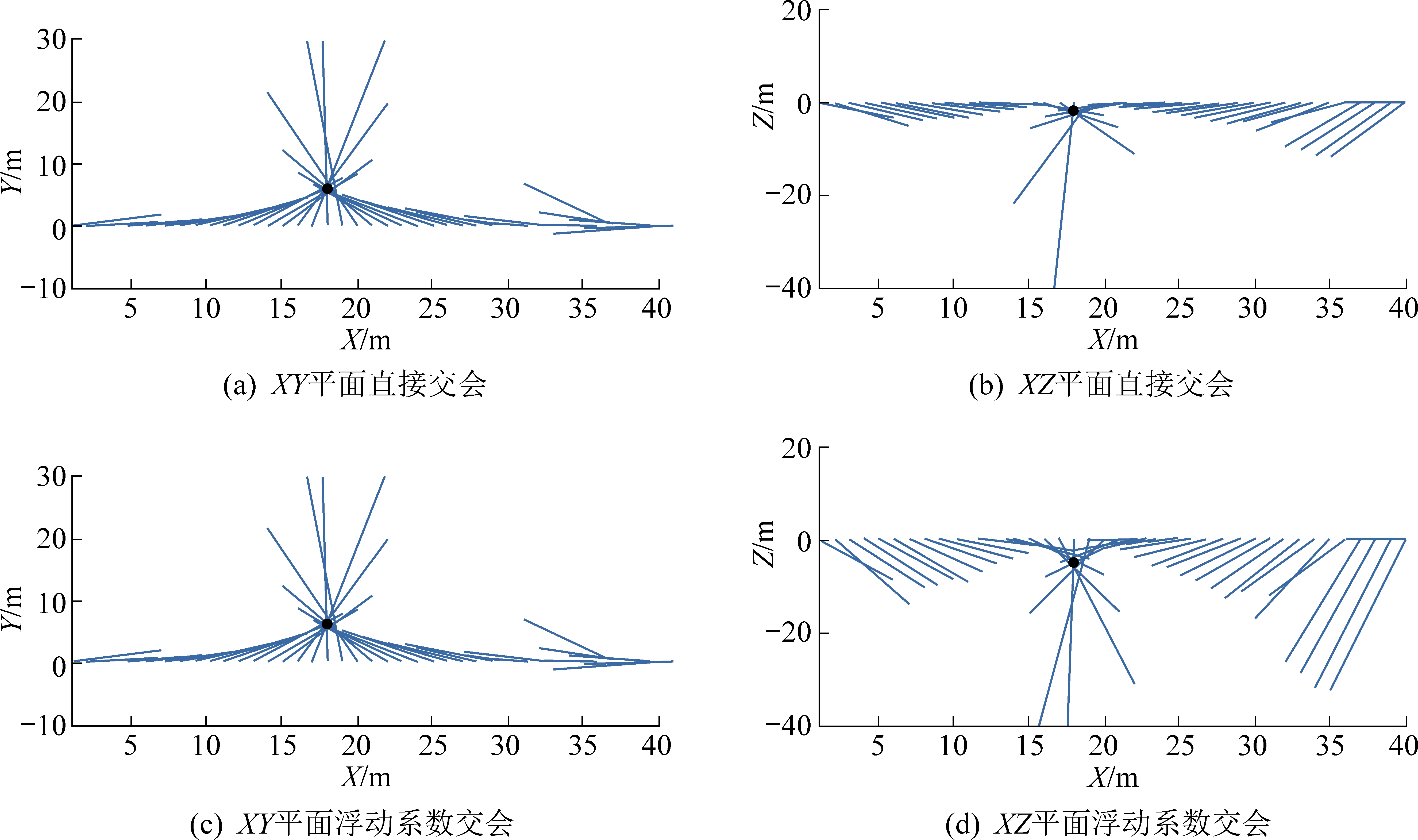
图12 矢量交会结果
Fig.12 Results of vector intersection
4 结 论
1)依据“等效涡流”理论,提出浮动系数矢量交会算法,通过对磁感应强度Bz数据的修正,使得磁感应强度Bx、By的合成矢量Bxz能准确地交会于异常体XZ平面投影坐标,从而定位异常体中心位置。
2)通过正演计算和物理模拟试验可知,该方法不需要先验信息,可以快速、准确定位异常体中心,是一种探测孔旁异常体的有效方法,因此可以考虑用于煤矿超前探测。
3)在实际探测中,由于无法准确计算背景场,异常场较难提取,需要进一步研究异常场提取的方法。
[1] 蒋邦远.实用近区磁源瞬变电磁法勘探[M].北京:地质出版社,1998.
[2] EADIE T,STALTARI G.Introduction to down-hole electromagnetic methods[J].Exploration Geophysics,1987,18(3):247-254.
[3] 李 文.煤矿采空区地面综合物探方法优化研究[J].煤炭科学技术,2017,45(1):194-199.
LI Wen.Optimization study of surface comprehensive geophysical detection methods of coal mine goafs[J].Coal Science and Technology,2017,45(1):194-199.
[4] 牟 义.浅埋采空区瞬变电磁法响应特征试验研究[J].煤炭科学技术,2018,46(10):203-208.
MOU Yi.Experimental study on response characteristics of transient electromagnetic method in shallow gob[J].Coal Science and Technology,2018,46(10):203-208.
[5] 朱宁军.地面巷道瞬变电磁探测一维正反演解释方法研究[D].徐州:中国矿业大学,2015.
[6] 王 鹏.积水采空区地井瞬变电磁法探测[J].煤炭技术,2017,36(6):140-142.
WANG Peng.Surface-hole TEM for detection of coal mine water collecting area [J].Coal Technology,2017,36(6):140-142.
[7] WOODS D V.A model study of the crone borehole pulse electromagnetic(PEM)system[D].Ontario:Queen’s University,1975.
[8] BARNETT C T.Simple inversion of time-domain electromagnetic data[J].Geophysics,1984,49(7):925-933.
[9] DUNCAN A C.Interpretation of down-hole transient EM data using current filaments[J].Exploration Geophysics,1987,18(2):36-39.
[10] FULLAGAR P K.Inversion of down-hole TEM data using circular current filaments[J].Exploration Geophysics,1987,18(3):341-344.
[11] CULL J P.Down-hole three component TEDM probes[J].Exploration Geophysics,1993,24:437-442.
[12] HUGHES N A,RAVENHURST W.Three component DHEM surveying at Balcooma[J].Exploration Geophysics,1996,27(3):77-89.
[13] VELLA L.Taking down-hole EM underground,at hill 50 decline,mount magnet,western Australia[J].Exploration Geophysics,1996,28:141-146.
[14] ELDERS J,WELLINGTON A.An application of reverse coupling to increase signal strength beneath conductive sediments-Miitel Mine,Kambalda,W A[J].Exploration Geophysics,1998,29(4):355-360.
[15] 程久龙,李明星,肖艳丽,等.全空间条件下矿井瞬变电磁法粒子群优化反演研究[J].地球物理学报,2014,57(10):3478-3484.
CHENG Jiulong,LI Mingxing,XIAO Yanli,et al.Study on particle swarm optimization inversion of mine transient electromagnetic method in whole-space[J].Chinese Journal of Geophysics,2014,57(10):3478-3484.
[16] 孟庆鑫,潘和平,牛 峥.大地介质影响下地—井瞬变电磁的正演模拟分析[J].中国矿业大学学报,2014,43(6):1113-1119.
MENG Qingxin,PAN Heping,NIU Zheng.Forward simulation of surface-borehole TEM in geological medium effect[J].Journal of China University of Mining &Technnology,2014,43(6):1113-1119.
[17] 杨海燕,徐正玉,岳建华,等.覆盖层下三维板状体地-井瞬变电磁响应[J].物探与化探,2016,40(1):190-196.
YANG Haiyan,XU Zhengyu,YUE Jianhua,et al.3D inclined conductor behavior of down-hole transient electromagnetic method with overburden layer[J].Geophysical and Geochemical Exploration,2016,40(1):190-196.
[18] 李大俊,翁爱华,杨 悦,等.地—井瞬变电磁三维交错网格有限差分正演及响应特性[J].吉林大学学报(地球科学版),2017,47(5):224-233.
LI Dajun,WENG Aihua,YANG Yue,et al.Three-dimension forward modeling and characteristics for surface-borehole transient electromagnetic by using staggered-grid finite difference method[J].Journal of Jilin University(Earth Science Edition),2017,47(5):224-233.
[19] 孟庆鑫,潘和平.地—井瞬变电磁响应特征数值模拟分析[J].地球物理学报,2012,55(3):1046-1053.
MENG Qingxin,PAN Heping.Numerical simulation analysis of surface-hole TEM responses[J].Chinese Journal of Geophysics,2012,55(3):1046-1053.
[20] 杨 毅,邓晓红,张 杰,等.一种井中瞬变电磁异常反演方法[J].物探与化探,2014,38(4):855-859.
YANG Yi,DENG Xiaohong,ZHANG Jie,et al.A borehole TEM anomaly inversion method[J].Geophysical and Geochemical Exploration,2014,38(4):855-859.
[21] 李建慧,刘树才,焦险峰,等.地—井瞬变电磁法三维正演研究[J].石油地球物理勘探,2015,50(3):556-564.
LI Jianhui,LIU Shucai,JIAO Xianfeng,et al.Three-dimensional forward modeling for surface-borehole transient electromagnetic method[J].Oil Geophysical Prospecting,2015,50(3):556-564.
[22] 徐正玉,杨海燕,邓居智,等.垂直接触带影响下地-井瞬变电磁响应研究[J].地球物理学进展,2015,30(3):1345-1353.
XU Zhengyu,YANG Haiyan,DENG Juzhi,et al.Research on response of down-hole TEM by vertical sheet[J].Progress in Geophysics,2015,30(3):1345-1353.
[23] 李 凯,孙怀凤.矿井含水构造地井瞬变电磁响应规律分析[J].中国矿业大学学报,2018,47(5):1113-1122.
LI Kai,SUN Huaifeng.Response characteristics analysis of mine water filled structure with ground-tunnel transient electromag-netic method[J].Journal of China University of Mining &Technology,2018,47(5):1113-1122.
[24] 姚伟华,王 鹏,李明星,等.地孔瞬变电磁法超前探测数值模拟响应特征[J].煤炭学报,2019,44(10):3145-3153.
YAO Weihua,WANG Peng,LI Mingxing,et al.Numerical simulation response characteristics of down-hole TEM for advanced detection[J].Journal of China Coal Society,2019,44(10):3145-3153.
[25] 姚伟华,王 鹏,李明星,等.三分量地-孔瞬变电磁法积水采空区探测试验[J].煤田地质与勘探,2019,47(5):54-62.
YAO Weihua,WANG Peng,LI Mingxing,et al.Experimental study of three-component down-hole TEM for detecting water-filled goaf[J].Coal Geology &Exploration,2019,47(5):54-62.
[26] 张 杰.地-井瞬变电磁异常特征分析及矢量交会解释方法研究[D].北京:中国地质大学(北京),2009.
[27] 张 杰,邓晓红,谭捍东,等.地—井瞬变电磁资料矢量交会解释方法[J].物探与化探,2015,39(3):572-579.
ZHANG Jie,DENG Xiaohong,TAN Handong,et al.A study of vector intersection for borehole transient electromagnetic method[J].Geophysical and Geochemical Exploration,2015,39(3):572-579.
