0 引 言
大地电磁测深(Magnetotelluric，MT)是一种发展较早的地球物理勘探方法，该方法利用天然的电磁场作为场源进行研究地球内部的电性结构，如今已广泛应用于固体矿产的勘察、石油天然气的勘探等各个领域[1-2]。大地电磁反演是大地电磁测深的关键步骤之一，而反演算法的优劣将直接影响最后的解释结果。目前，大地电磁反演算法可分为线性算法和非线性算法，这2种算法的区别在于是否对目标函数进行线性化处理[3]。一维典型的线性反演算法包含Occam法，马夸特法(Marquart)，正则化方法等[4-6]。但是反演问题本身存在非线性、不适定性和解的非一性等问题，因此线性化反演算法容易使反演陷入局部极小值，并且线性算法反演是否成功还依赖于对初始模型的选择。为了克服线性算法的缺陷，一些学者将遗传算法[7]、模拟退火法[8]、粒子群算法[9]、差分进化算法[10-11]、人工鱼群算法[12]、神经网络[13]和一些改进的群智能算法[14-17]引入大地电磁的反演之中，并取得较好的效果。
目前，单一非线性算法针对大地电磁进行反演时仍然存在收敛速度慢，求值精度低，尤其是随着反演层数的增多，会导致反演的维度增加，这使得单一的非线性算法很难满足反演精度和效率的需求。相关学者已经结合其他算法对单一的非线性智能算法进行改进并应用到反演中[18-20]。在综合研究非线性算法发现，粒子群算法(Particle Swarm Optimization，PSO)和差分进化算法(Differential Evolution，DE)尽管都有着良好的全局搜索能力，但是这2种算法也都有着自身的缺陷。如PSO算法极易陷入局部极小值而且寻优结果不稳定；DE算法容易陷入停滞和早熟状态，而且在搜索速度上较PSO慢，同时这2种算法对局部的寻优能力也相对较差。因此本文针对算法问题，提出了一种混合智能算法(Hybrid Intelligent Algorithm，HIA)。HIA算法融合了PSO算法和DE算法对全局进行迭代寻优的搜索能力，让两种算法进行优势互补，同时又利用Nelder-Mead优化算法对寻优结果进行局部寻优，使得算法能够快速的收敛到最优值，而且在进行大地电磁反演时，引入正则化因子，可以有效地避免反演问题的非唯一性。笔者详细地叙述了HIA算法的工作原理，通过多维函数、地电模型以及实测数据对HIA算法进行验证。
1 HIA算法的原理和实现
1.1 PSO算法原理
PSO算法自1995年由Kennedy和Eberhart提出以来，被广泛的应用于各领域。PSO算法在进行迭代时，主要是利用速度和位置的更新来完成对适应值函数的寻优。
粒子群的速度和位置的更新公式如下：
(1)
(2)
式中：
和
是第i个粒子在k+1次迭代的速度和位置(i=1,2,…,Np,k=1,2,…,K),Np为种群个数，K为最大迭代次数;ω为惯性因子；c1和c2均为学习因子；r1和r2为(0,1)之间的随机数；
为第k次迭代的第i个种群当前的个体极值；
为第k次迭代的全局极值；γ为约束因子，用于控制权重，取γ=1。
PSO算法中，ω越大，粒子飞行的速度越大，粒子会以较大的步长对全局进行搜索，但是不利于收敛；反之，ω较小时，粒子的速度变小，位移变小，粒子相同迭代次数搜索范围缩小，体现了粒子的局部搜索能力。c1和c2分别表示粒子自身的学习能力和粒子间的相互学习能力，因此惯性权重ω、c1和c2共同维护着粒子对全局和局部的平衡。为了保持算法的稳定，文献[21]利用式(3)来确定三者的关系：
(3)
1.2 DE算法原理
DE算法由Rainer Storn和Kenneth Price两位学者在遗传算法的基础上提出来，基本的流程包含变异、交叉和选择。关于差分进化的具体描述如下：
1)初始化。在D维的空间中，对Np个个体进行初始化，具体产生方式如下：
(4)
式中：
表示第i个个体的第j维；
和
分别为给定个体的最大值和最小值；r为(0,1)之间的随机数。
2)变异。从种群中随机选取3个不同的个体，xr1、xr2、xr3(r1≠r2≠r3)，式(4)产生变异个体vi，具体如下：
(5)
式中：F为变异因子。
3)交叉。具体公式如下：
(6)
式中：CR∈(0,1)为交叉因子；rang(j)为[1,2,…，D]的随机整数。
4)选择。用交叉后的个体
和上一代的个体
的适应值函数作比较，函数值较小的进入下一代的种群：
(7)
5)迭代停止。若种迭代次数达到最大迭代数K或者停机条件则寻优结束，否则转入步骤2)，开始下一轮的迭代。
1.3 Nelder-Mead优化算法
Nelder-Mead优化算法是一种面向局部的搜索方法，而且有较高的搜索速率。其核心思想是：在n维的搜索空间中，随机的生成有n+1个顶点相互连接生成简单的多面体。记xl为多面体的顶点，l=0,1,…,n，根据适应值函数计算f(xl)，假设f(x0)≤f(x1)≤…≤f(xn)。其中，x0为最优点，xn为最差点，然后经过反射、扩张、压缩等操作寻找极小值点，关于顶点的更新的步骤如下：
1)计算除了最差点xn以外的其他n个顶点的重心
2)反射操作：令
为反射系数，一般取α=1。若f(xn+1)<f(x0)，转到步骤3)；若f(x0)≤f(xn+1)<f(xn-1)，则用xn+1替代xn，重新生成多面体，转到步骤1)；若f(xn+1)≥f(xn-1)，则转到步骤4)。
3)扩张操作：令
为扩张系数，一般取2。若f(xn+2)<f(xn+1)，则用xn+2替代xn，重新生成多面体，转到步骤1)；若f(xn+2)≥f(xn+1)，则用xn+1替代xn，重新生成多面体，转到步骤1)。
4)压缩操作：若f(xn+1)≥f(xn-1)且f(xn+1)<f(xn)，则
则
(可以取0.5)为压缩系数。若f(xn+3)≤f(xn)，则用xn+3替代xn，生成新的多面体，转到步骤1)；若f(xn+3)>f(xn)，则转到步骤5)。
5)令xq=x0+(xq-x0)，其中,q=0,1,…,n，形成新的多面体，重新计算f(xl)转步骤1)。
1.4 HIA工作步骤
HIA算法是结合了PSO算法和DE算法的全局搜索能力和Nelder-Mead优化算法的局部搜索能力而形成的一种的混合算法。HIA算法融合了2种算法对全局进行寻优的优点，既能够很大程度上避免了PSO算法容易陷入局部最小的缺点，又弥补了DE算法寻优效率和容易早熟的不足，同时引入Nelder-Mead优化算法进行局部搜索，提高了算法整体的稳定性和鲁棒性，进一步保证了算法寻优的效率和结果的正确性。HIA算法工作步骤如下：
1)首先固定种群Np、最大迭代次数K、交换周期τ和搜索条件算子ps(0<ps<1)，搜索条件算子ps作为判定是否进入Nelder-Mead优化算法进行迭代寻优的条件算子，目标函数值Eva，其中最大迭代次数K和目标函数值Eva作为停机条件。初始化种群Np、PSO和DE算法的参数，将种群Np均匀分成2组。
2)利用目标函数计算每个种群的适应度函数值，判断是否满足停机条件。若满足，保存最优值，循环结束；若不满足停机条件，则进入下一步骤3)。
3)将Np/2种群利用PSO算法进行迭代寻优，判断是否满足r<ps(r是(0,1)之间的随机数)，若满足则进行Nelder-Mead优化算法搜索；若不满足，转下一步骤4)。
4)剩余Np/2种群利用DE算法进行迭代寻优，然后判断是否满足r<ps，若满足则进行Nelder-Mead优化算法搜索，若不满足，转下一步骤5)。
5)判断算法是否迭代了τ次，若满足，将种群Np进行重组，然后再将Np随机均匀分配成2组，转到步骤2)；若不满足，直接转步骤2)。
1.5 HIA算法测试
为了测试HIA算法的算法性能，用Rastrigin函数对算法进行验证。Rastrigin函数常用来评价优化算法处理复杂问题的能力，此外，函数会因为维度不同而存在许多局部极小值点，但其全局极小值点只有0。函数的表达式如下：
(8)
式中：j=1,2,…D为函数的维度；对于R(X)，xj∈(-5.12,5.12)。
为了彰显混合智能算法的优势，将HIA算法寻优得到的结果与文献[9]中提出的阻尼PSO算法和DE算法的寻优结果进行对比。为保证算法结果对比的可靠性，3种算法设置共同参数，最大迭代次数K=1 000,种群Np=60，ps=0.1，停止条件为1×10-20。在进行HIA迭代时，交换周期τ=250,函数的维度D=15。考虑到算法的随机性，该算法独立运行80次的平均值作为最终输出结果，具体见表1。
表1 Rastrigin函数的寻优结果对比
Table 1 Comparison of optimization results of Rastrigin function
测试函数函数维度寻优算法最优值Rastrigin15阻尼PSO9.211DE0.214HIA0
由表1可得，对于Rastrigin函数的寻优，HIA算法可以准确的求得函数的全局极小值，而阻尼PSO算法和DE算法都没有收敛到全局极小值点。图1给出了3种算法的迭代下降曲线。由图1可得，HIA算法会在迭代800多次时就达到停机条件，而阻尼PSO算法，直接陷入了局部极小值；DE算法的迭代曲线虽然仍在下降，但是算法的收敛速度和寻优结果都不理想。因此，HIA算法无论是寻优效率还是寻优结果都明显优于阻尼PSO算法和DE算法。
图1 Rastrigin函数的迭代下降曲线
Fig.1 Iterative descent curves of Rastrigin function
2 理论模型的演算与分析
2.1 反演问题的实现
在地球物理反演中，目标函数通常采用以下形式：
Φ=Φd+λΦm
(9)
式中：Φd是数据的拟合差；Φm是模型的拟合差；λ为正则化因子；m是模型向量，引入模型拟合差可以有效避免反演的多解性。
对于一维r层地电断面而言，模型向量m表示为
m=(ρ1，ρ2，…ρr，h1,h2,…hr-1)
(10)
一维反演数据拟合差Φd表达式为
(11)
式中：NT为频点个数；
分别为第t个频点的观测视电阻率与相位；
分别为第t个频点的计算视电阻率与相位。
根据不同的约束条件，模型拟合差Φm的约束有很多种，常用的有3种，模型参数的平方和最小，模型参数导数的平方和最小和模型参数二阶导数的平方和最小。在此选取最小模型的约束函数，式中，mref为背景模型。
Φm=‖m-mref‖2
(12)
对于正则化因子的选取，本文采取文献[5]提出的自适应调节正则化因子的调节方法，该方法在一定程度上同时满足了使Φd和Φm极小的条件，而且能很好的拟合数据和压制模型的冗余构造。具体公式如下：
(13)
2.2 四层地电模型
文中数值模型反演程序在Intel(R)Core(TM)i5-7200 2.5GHz(四核)上运行。
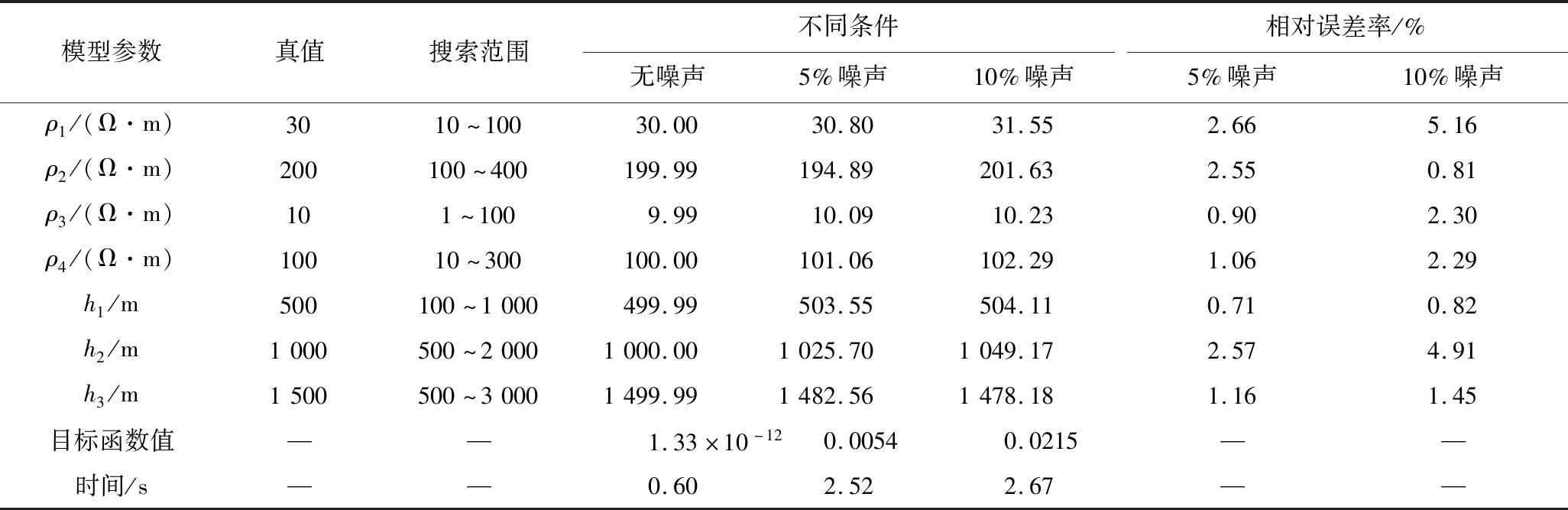
1)HIA反演分析。本文采用HIA算法对一维四层地电模型(KH)进行反演。首先对不含噪声的模型进行反演，并把正演理论数据作为反演的观察数据。为了模拟真实的观测数据和验证算法的鲁棒性，笔者对理论数据分别添加5%和10%的随机的噪声进行反演，反演结果见表2。在HIA算法进行反演时，搜索范围的上下限与真实值相差2倍或2倍以上。反演中选取的种群个数Np=60，K=100，交换次数τ=30，搜索算子ps=0.1，初始正则化因子λ=0.5。在进行无噪声反演时，设定目标函数的停止条件为1×10-10。为了保证反演结果的可靠性，文中对观测数据进行了80次反演，并把80次反演结果的平均值作为最终的结果。具体结果见表2。由表2的反演结果可知，HIA算法在不含噪的条件下能够完全的反演出四层的地电模型，而且反演所需要的时间也很短。在含5%和10%的噪声下，反演结果的最大误差率分别为2.66%和5.16%。由此可以得出，噪声对反演结果虽然有一定的影响，但是HIA算法也能够反演出KH模型,可见HIA具有良好的鲁棒性。图2给出了HIA算法反演在添加10%的噪声的视电阻率拟合曲线、相位拟合曲线。
表2 四层地电模型HIA算法反演结果
Table 2 Inversion results of HIA algorithm for four-layer geoelectric model
模型参数真值搜索范围不同条件无噪声5%噪声10%噪声相对误差率/%5%噪声10%噪声ρ1/(Ω·m)3010～10030.0030.8031.552.665.16ρ2/(Ω·m)200100～400199.99194.89201.632.550.81ρ3/(Ω·m)101～1009.9910.0910.230.902.30ρ4/(Ω·m)10010～300100.00101.06102.291.062.29h1/m500100～1000499.99503.55504.110.710.82h2/m1000500～20001000.001025.701049.172.574.91h3/m1500500～30001499.991482.561478.181.161.45目标函数值——1.33×10-120.00540.0215——时间/s——0.602.522.67——
图2 四层含10%噪声地电模型HIA算法反演拟合结果
Fig.2 HIA algorithm for inverse fitting of four-layer geoelectric model with 10% noise
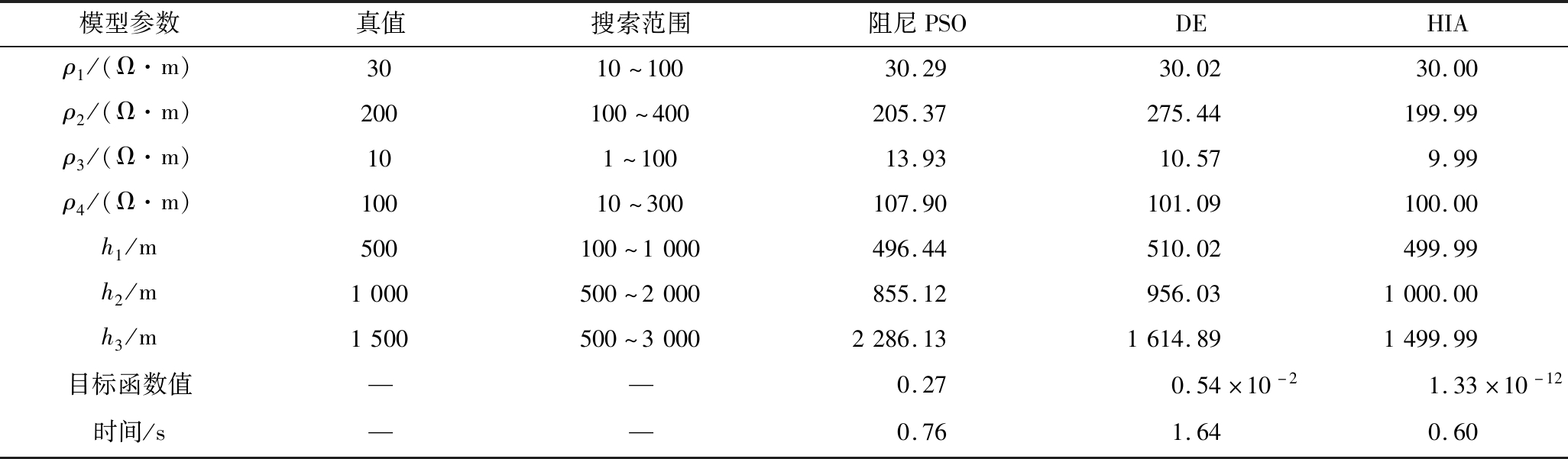
2)HIA与PSO和DE对比分析。为了彰显改进算法的优势，分别将四层地电模型在不含噪声的条件下与阻尼PSO算法和DE算法的反演结果进行了对比。同时，笔者为保证反演结果的可靠性，三种算法设置相同的参数，具体和式(1)中一致。3种算法分别独立进行80次反演，并把反演结果的平均值作为输出结果。表3给出了3种算法反演的对比结果，图3分别给出了3种算法的反演迭代收敛对比曲线和反演结果对比曲线。由表3的反演结果可知，相同的迭代次数下，HIA算法几乎可以恢复地下的模型，时间上也比DE反演和阻尼PSO反演较快。由图3的反演结果可以得到，HIA算法在进行迭代17次就达到了停止条件，反演结果几乎和理论模型重合，而阻尼PSO算法和DE算法反演的结果相对较差。由此可见，HIA算法比单独的DE算法和阻尼PSO算法在大地电磁反演方面具有优势。
表3 四层地电模型不同算法反演结果对比
Table 3 Comparison of inversion results of different algorithms for four-layer geoelectric model
模型参数真值搜索范围阻尼PSODEHIAρ1/(Ω·m)3010～10030.2930.0230.00ρ2/(Ω·m)200100～400205.37275.44199.99ρ3/(Ω·m)101～10013.9310.579.99ρ4/(Ω·m)10010～300107.90101.09100.00h1/m500100～1000496.44510.02499.99h2/m1000500～2000855.12956.031000.00h3/m1500500～30002286.131614.891499.99目标函数值——0.270.54×10-21.33×10-12时间/s——0.761.640.60
图3 四层地电模型不同算法反演的对比曲线
Fig.3 Contrast curves inverted by different algorithms for four-layer geoelectric model
2.3 实测数据反演
为进一步验证算法的可行性，利用HIA算法对实测数据进行反演。实测数据来自文献[5],取自吉林桦皮厂地热田的一个实测点数据，由钻井资料可知，地下电阻率大概呈现“高低高低”的纵向分布。采用HIA算法反演的参数设置为Np=60，K=400，交换次数τ=100，单纯形搜索算子ps=0.1，初始正则化因子λ=0.5。在算法进行反演时，采用一个六层的地电模型进行拟合反演，并将反演结果和目前常用的实测反演算法Bostick反演以及Occam的反演的结果进行了对比，图4给出了3种算法的视电阻率和相位的拟合曲线。由图4a的视电阻率曲线的拟合结果可知，Occam反演结果和本文HIA算法的反演结果效果较佳，但是Occam的高频部分拟合较差，而本文算法高低频的拟合效果都很好；由图4b相位曲线的拟合结果可以得出，Bostick和本文算法反演结果较好，但是Bostick在高低频的拟合效果较好，中频的拟合效果较差，而HIA算法虽然低频效果较Bosick的结果差，总体效果却是最佳的。采用式(11)计算3种算法的拟合差，Occam的结果为8.78，Bostick的结果为2.36，而HIA算法结果为0.781 5。由此可得，本文算法用于实测大地电磁的反演也是十分有效的。
图4 实测数据反演结果对比
Fig.4 Comparison of measured data inversion results
3 结 论
1)提出了混合HIA算法解决了PSO算法和DE算法寻优效率低和易陷入局部极小值的问题。通过对多维函数和理论模型进行对比试验，证明了HIA算法比这2种算法反演的寻优效率更高。
2)利用HIA算法对实测点数据进行反演，反演结果表明，HIA反演结果与实测数据更加吻合。
3)考虑到二维或三维更符合实际的地质情况，将来可以对HIA算法进一步研究，以便能够拓展到高维反演。
[1] 汤井田，任政勇，周 聪，等.浅部频率域电磁勘探方法综述[J].地球物理学报,2015,58(8):2681-2705.
TANG Jingtian,REN Zhengyong,ZHOU Cong,et al.Frequency-domain electromagnetic methods for exploration of the shallow subsurface:a review[J].Chinese Journal of Geophysics,2015,58(8):2681-2705.
[2] 叶高峰，王 辉，郭泽秋.长周期大地电磁测深数据采集及处理技术[J].地球物理学进展，2013，28(3):1219-1226.
YE Gaofeng,WANG Hui,GUO Zeqiu,et al.Data acquisition and processing technology of long-period magnetotclluric [J].Progressin Geophys,2013,28(3):1219-1226.
[3] 陈 理，秦其明，王 楠.大地电磁测深正演和反演研究综述[J].北京大学学报(自然科学版),2014,50(5):979-984.
CHEN Li,QIN Qiming,WANG Nan.Review of the forward modeling and inversion in magnetotelluric sounding field[J].Acta Scientiarum Naturalium Universitatis Pekinensis,2014,50(5):979-984.
[4] CONSTABLE S C,PARKER R L,CONSTABLE C G.Occam's inversion:a practical algorithm for generating smooth models from EM sounding data[J].Geophysics,1987,52(3):289-300.
[5] 陈小斌.大地电磁正反演新算法研究及资料处理与解释的可视化集成系统开发[D].北京：中国地震局地质研究所,2003.
[6] 冯思臣，王绪本，阮 帅.一维大地电磁测深几种反演算法的比较研究[J].石油地球物理勘探,2004,39(5):594-599.
FENG Sichen,WANG Xuben,RUAN Shuai.Comparison among several inversion algorithms of 1D MT[J].Oil Geophysical Prospecting,2004,39(5):594-599.
[7] 刘云峰，曹春蕾.一维大地电磁测深的遗传算法反演[J].浙江大学学报,1997,31(3):300-305.
LIU Yunfeng,CAO Chunlei.Inversion of one-dimensional MT data using genetic algorithms[J].Journal of Zhejiang University,1997,31(3):300-305.
[8] 师学明，王家映.一维层状介质大地电磁模拟退火反演法[J].地球科学:中国地质大学学报,1998,23(5):543-545.
SHI Xueming,WANG Jiaying.One dimensional magnetotelluric sounding inversion using simulated anneaking[J].Earth Science：Journal of China University of Geoscience,1998,23(5):543-545.
[9] 师学明，肖 敏，范建柯，等.大地电磁阻尼粒子群优化反演法研究[J].地球物理学报,2009,52(4):1114-1120.
SHI Xueming,XIAO Min,FAN Jianke,et al.The damped PSO algorithm and its application for magnetotelluric sounding data inversion[J].Chinese Journal of Geophysics,2009,52(4):1114-1120.
[10] 王天意,杨 进,颜廷杰,等.地球物理反演中的差分进化算法[J].地质与勘探,2014,50(5):971-975.
WANG Tianyi,YANG Jin,YAN Tingjie,et al.The differential evolution algorithm in geophysical inversion[J].Geology and Prospecting,2014,50(5):971-975.
[11] XIONG Jie,Member,IAENG,et al.A non-linear geophysical inversion algorithm for the MT data based on improved differential evolution[J].Engineering Letters,2018,26(1):161-170.
[12] 胡祖志,何展翔,杨文采,等.大地电磁的人工鱼群最优化约束反演[J].地球物理学报,2015,58(7):2578-2587.
HU Zuzhi,HE Zhanxiang,YANG Wencai,et al.Constrained inversion of magnetotelluric data with the artificial fish swarm optimization method[J].Chinese Journal of Geophysics,2015,58(7):2578-2587.
[13] 王 鹤,蒋 欢,王 亮,等.大地电磁人工神经网络反演[J].中南大学学报:自然科学版,2015,46(5):1707-1714.
WANG He,JIANG Huan,WANG Liang,et al.Magnetotelluric inversion using artificial neural network[J].Journal of Central South University(Science and Technology),2015,46(5):1707-1714.
[14] GODIO A,SANTILANO A.On the optimization of electromagnetic geophysical data:application of the PSO algorithm[J].Journal of Applied Geophysics,2018,148:163-174.
[15] LI Siyu,WANG Shuming,WANG Pengfei,et al.An improved grey wolf optimizer algorithm for the inversion of geoelectrical data[J].Acta Geophysica,2018,66(4):607-621.
[16] 孙欢乐，王世彪，郭荣文，等.基于自适应纯形模拟退火法一维大地电磁测深视电阻率和相位反演研究[[J].物探化探计算技术,2016,38(5):584-592.
SUN Huanle,WANG Shibiao,GUO Rongwen,et al.One dimensional magnetotelluric sounding apparent resistivity and phase inversion of adaptive simplex simulated annealing study[J].Computing Techniques for Geophysical and Geochemical Exploration,2016,38(5):584-592.
[17] JAMASB A,MOTAVALLI-ANBARAN S H,Ghasemi K.A novel hybrid algorithm of particle swarm optimization and evolution strategies for geophysical non-linear inverse problems[J].Pure and Applied Geophysics,2019,176(4):1601-1613.
[18] 李明星.矿井瞬变电磁 PSO-DLS 组合算法反演研究[J].煤炭科学技术,2019,47(9):268-272.
LI Mingxing.Study on mine transient electromagnetic method inversion based on PSO-DLS combination algorithm[J].Coal Science and Technology,2019,47(9):268-272.
[19] DA Conceição Batista J,SAMPAIO E E S.Magnetotelluric inversion of one-and two-dimensional synthetic data based on hybrid genetic algorithms[J].Acta Geophysica,2019,67(5):1365-1377.
[20] LIU Jianxin,GUO Rongwen,TONG Xiaozhong,et al.A decorrelation-based hybrid global search algorithm for inversion of 1D magnetotelluric data[J].Journal of Geophysics and Engineering,2011,8(2):225-232.
[21] PEREZ R E,BEHDINAN K.Particle swarm approach for structural design optimization[J].Computers &Structures,2007,85(19/20):1579-1588.
