0 引 言
在矿井安全事故中，由于瓦斯引起的事故危害最大、破坏力最强、造成的后果最严重[1-4]，而工作面上隅角处瓦斯最易积聚超限[5]，采空区的瓦斯通过漏风风流涌向工作面，会导致采空区上隅角瓦斯大量积聚，从而上隅角瓦斯浓度过高，导致一系列危及生命财产安全的事故发生[6]。瓦斯抽采是解决采空区上隅角瓦斯大量积聚问题的重要手段，因为采空区瓦斯抽采的流量较大，具有稳定的来源[7-9]，采空区瓦斯抽采能直接切断采空区瓦斯流动路径，隔离通风盲区，防止瓦斯超限[10-12]。对工作面采空区进行瓦斯抽采时，虽然能够有效控制工作面瓦斯超限，但同时也会加速采空区遗煤的自燃[13-15]。由于采空区遗煤在自然状态下会消耗氧气释放热量，在采空区内部形成温度场。对采空区进行瓦斯抽采会导致采空区内压力场的变化，进而影响采空区内漏风风流的流动。采空区内漏风风流的流动变化会影响采空区内瓦斯浓度、氧气浓度和气体温度的分布情况。
在采空区流场数学模型的建立上，章梦涛等[16]将工作面和采空区视为不同的多孔介质，利用Darcy渗流定律建立了统一的采空区流场数学模型，利用有限单元法的基本思想进行了离散与求解；李宗翔等[17-20]利用空气和瓦斯混合气体渗流-扩散方程，建立了二维坐标系下的非均质状态的采空区流场数学模型，并结合现场观测对模拟结果进行了描述；王真等[21]利用Darcy渗流定律，建立了采空区流场数学模型，通过对数学模型的各种边值问题进行求解，分析得到采空区内气体的流动状态。以上学者取得了关于采空区瓦斯抽采研究的丰硕成果，但对考虑温度变化的采空区瓦斯抽采多场耦合数学模型研究甚少，未能考虑抽采引起漏风，漏风加剧遗煤氧化升温，氧化升温引起采空区气体压力场发生改变，压力场引起气体浓度场改变，浓度场的变化又会引起温度场的变化。
为此，笔者考虑采空区瓦斯抽采前后引起采空区温度场的变化，分析建立考虑温度变化的采空区瓦斯抽采多物理场耦合数学模型，离散数学模型并编制计算机解算软件，模拟U型通风方式下采空区深埋管瓦斯抽采物理模型，分析采空区瓦斯抽采前后的压力、瓦斯浓度、氧浓度、固体温度和气体温度分布情况及变化趋势，其结果可为采空区瓦斯抽采优化提供参考依据。
1 采空区瓦斯抽采多场耦合理论
在采空区内部，存在压力场、流场、气体浓度场和温度场的多场耦合作用，若有某一场的物理量发生变化，则其他场的物理量将相应地发生改变。如果对采空区内部进行瓦斯抽采，将会发生以下变化：①对采空区进行瓦斯抽采会引起采空区内压力场的变化，进而影响采空区内漏风风流的流动；②漏风风流的流动变化会影响采空区内瓦斯浓度、氧气浓度和气体温度的分布情况；③氧气浓度的变化会引起采空区内遗煤氧化放热变化，即影响采空区内固体温度分布变化；固体温度变化会引起采空区内遗煤氧化耗氧量的变化，进而影响采空区内氧气浓度的分布情况；④采空区内固体温度的变化会引起采空区内气体和固体的换热量的变化，进而影响采空区内气体温度的分布情况；气体温度的变化又会引起采空区内气体和固体的换热量的变化，进而影响采空区内固体温度的分布情况；⑤采空区内气体温度的变化还会引起气体密度的变化，进而影响流场的分布情况，即影响漏风风流的流动，进而影响瓦斯浓度、氧气浓度和气体温度的分布情况。采空区瓦斯抽采多场耦合理论关系如图1所示。
图1 采空区瓦斯抽采多场耦合关系
Fig.1 Multi-field coupling relationship of gas drainage in goaf
2 考虑温度变化的采空区瓦斯抽采的多场耦合数学模型
垮落煤岩的采动孔隙通常比其原有孔隙大，所以采空区内气体一般认为是在垮落煤岩的采动孔隙里渗流[22-24]，而且采空区内垮落煤岩的渗透率会呈现“O”形圈的分布[25]。
2.1 采空区流场平衡方程及边界条件
笔者选取的计算区域，其采空区深度即x轴方向上的长度为300 m，工作面长度即y轴方向上的长度为200 m，同时对边界条件进行划分，如图2所示。
图2 流场计算区域和边界条件
Fig.2 Calculate area and boundary conditions of flow field
根据Darcy渗流定律和压力势函数P，依据质量守恒定律可得平衡方程表达式为
(1)
式中：K为采空区内多孔介质的气体渗透系数，m/s；g为重力加速度，m/s2；p为采空区内气体的压力，Pa；ρ为采空区内气体的密度，kg/m3；α为采空区所属煤层倾角，(°)；S为控制体的单位面积，m2；Γ为二维流场控制体；ρCH4为瓦斯的密度，kg/m3；qv为采空区内遗煤的瓦斯解吸速率，m3/(s·kg)；ρm为采空区内遗煤的密度，kg/m3。
边界条件为
p|Γ1=P(x,y)|(x,y)∈Γ1
式中：P(x,y)为边界上各个位置的气体压力组成的已知函数；Γ1为第1类边界条件。
2.2 采空区瓦斯浓度场平衡方程及边界条件
基于Fick扩散定律和质量守恒定律，确定单位时间控制体内瓦斯含量的变化量等于漏风风流流入流出控制体时带入带出的瓦斯量之差、由于扩散运动而流入流出控制体的瓦斯量之差、控制体内的遗煤的瓦斯解吸量三者之和。即
(2)
式中：cCH4为采空区内瓦斯的质量浓度，kg/m3；vx和vy分别为采空区内气体在x方向上和y方向上的渗流速度，m/s；n为采空区内多孔介质的孔隙率，%；DCH4为采空区内瓦斯的扩散系数，m2/s。
采空区瓦斯浓度场的计算区域与采空区流场的计算区域相同，其边界条件划分如图3所示。考虑到Γ1边界上、下2段的风流方向不同，故将其分为Γs和Γx两个边界。
图3 瓦斯浓度场计算区域和边界条件
Fig.3 Area and boundary conditions of gas concentration field
边界条件有
式中，Γx为边界视为第1类边界条件。
2.3 采空区氧气浓度场平衡方程及边界条件
根据质量守恒定律可知：单位时间内，控制体内氧气含量的变化量等于漏风风流流入流出控制体时导致的氧气量之差、氧气扩散时导致的氧气量之差、控制体内的遗煤的氧化耗氧量三者之和。即：
(3)
式中：cO2为采空区内氧气的质量浓度，kg/m3；DO2为采空区内氧气的扩散系数，m2/s；u(t)为单位时间内单位体积的采空区内遗煤的耗氧量，kg/(s·m3)。
采空区氧浓度场的计算区域与采空区流场的计算区域相同，其边界条件划分同采空区瓦斯浓度场一致。边界条件为
式中：cO2(x,y)为边界上各个位置的氧气质量浓度组成的已知函数，Γx边界视为第一类边界条件。
2.4 采空区固体温度场平衡方程及边界条件
根据Fourier导热定律和能量守恒定律得控制体内固体能量的变化量等于控制体内导入导出固体的热量差加上控制体内采空区遗煤的氧化放热量减去控制体内气固两项间的对流换热量。即：
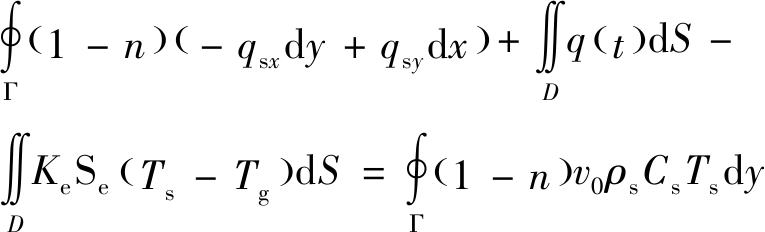
(4)
式中：qsx、qsy分别为采空区内固体颗粒在x方向上和y方向上的热流密度，W/m2；Ts为采空区内固体颗粒的温度，K；Se为控制体的比表面积，m-1；q(t)为单位时间内单位体积的采空区内遗煤的氧化放热量，W/m3；Ke为采空区内固体颗粒和气体的对流换热系数，W/(m2·K)；Tg为采空区内气体的温度，K；v0为工作面的推进速度，m/s；ρs为采空区内固体颗粒的密度，kg/m3；Cs为采空区内固体颗粒的比热容，J/(kg·K)。
由于采空区内固体不仅在采空区内部进行热量交换，还会和采空区上下边界附近的煤体进行热量交换，所以对采空区固体温度场进行计算时，上下边界需要拓展至热流密度为0处。本文中采空区固体温度的计算区域和其边界条件划分如图4所示。
图4 固体温度场计算区域和边界条件
Fig.4 Calculation area and boundary conditions of solid temperature field
对于Γx边界，其位于液压支架后端，各点的固体视为刚刚垮落的煤岩，其温度可以直接使用仪器测得，视为第1类边界条件；对于Γ7、Γ8边界，边界上各点在y方向上的热流通量为0；对于Γs、Γ4、Γ5、Γ6、Γ9、Γ10边界，边界上各点在x方向上的热流通量为0，有
式中，ts(x,y)为边界上各个位置的固体温度组成的已知函数。
2.5 采空区气体温度场平衡方程及边界条件
根据Fourier导热定律和能量守恒定律得到采空区气体温度场平衡方程为
(5)
式中：qgx、qgy分别为采空区内气体在x方向上和y方向上的热流密度，W/m2；Cg为采空区内气体的比热容，J/(kg·K)。
采空区气体温度场的计算区域与采空区瓦斯浓度场的计算区域与边界条件相同。
边界条件为
式中，tg(x,y)为边界上各个位置的气体温度组成的已知函数。
2.6 考虑温度变化的采空区瓦斯抽采的多场耦合数学模型
采空区瓦斯抽采时会受到采空区内多个物理场耦合作用的影响，将这几个场的数学模型进行联立,得到考虑温度变化的采空区瓦斯抽采的多场耦合数学模型：
边界条件为：
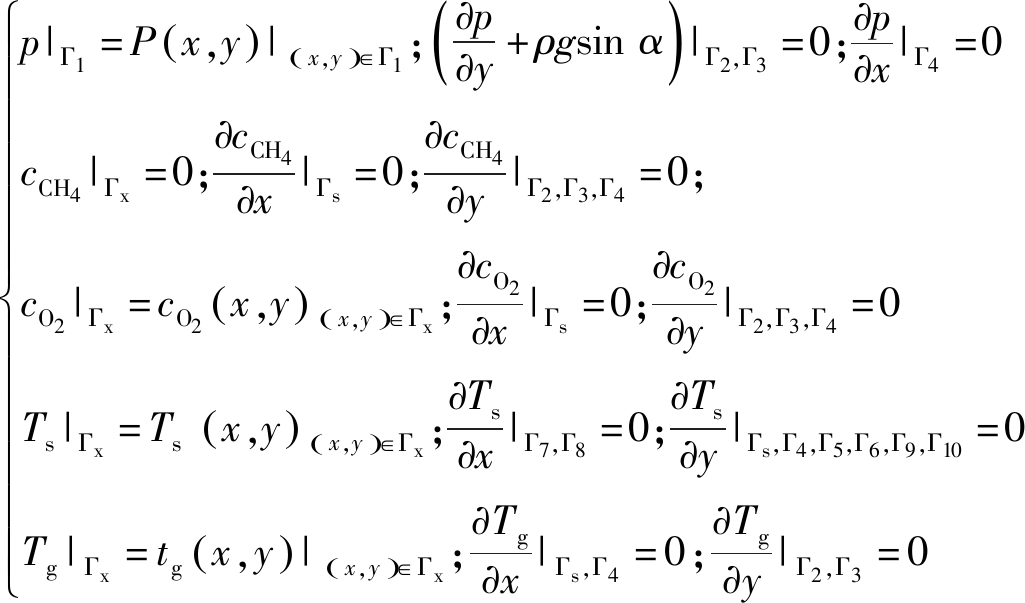
3 考虑温度变化的采空区瓦斯抽采模型的离散化
3.1 网格划分
采用“先矩形后三角形”的网格划分方法，同时根据计算区域的实际情况，在状态变化剧烈的位置进行密集划分、变化平缓的位置进行稀疏划分，其中靠近工作面中轴线处较密集，靠近采空区上下边界处较稀疏。具体划分情况如图6所示。
笔者采取从下到上、从左到右的编号原则对计算区域内的各个节点和单元进行编号。
图6 计算区域的网格划分情况
Fig.6 Meshing situation of calculation area
3.2 平衡方程离散
笔者根据插值函数三角形单元对平衡方程和边界条件进行离散。假设计算区域内压力是关于x和y的一次函数。在计算区域内任取一个三角形单元，设其压力为P，关联的3个节点的压力为Pi、Pj和Pm，那么可以得到
(6)
式中：ai=xjym-xmyj；aj=xmyi-xiym；am=xiyj-xjyi；bi=yj-ym；bj=ym-yi；bm=yi-yj；ci=xj-xm；cj=xi-xm；cm=xj-xi；xi、xj、xm分别为关联的3个节点i、j、m的横坐标值；yi、yj、ym分别为关联的3个节点i、j、m的纵坐标值。
3.2.1 采空区流场平衡方程离散
采空区流场平衡方程离散结果表示为
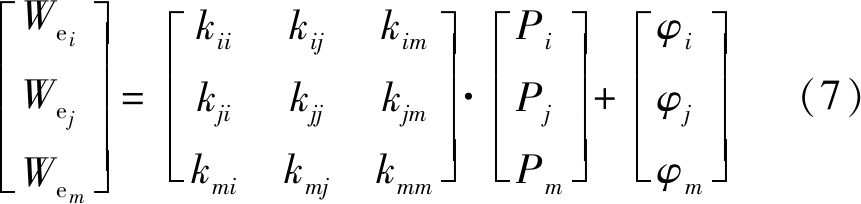
式中：
且
分别为三角形单元控制体对节点i、j、m的压力贡献值。
3.2.2 采空区瓦斯浓度场平衡方程离散
采空区瓦斯浓度场平衡方程离散结果表示为
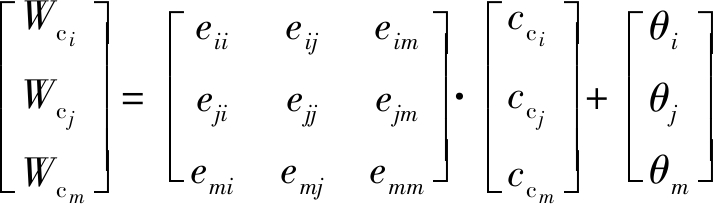
(8)
式中：
且
分别为关联的3个节点i、j、m的瓦斯体积分数；Wci、Wcj、Wcm分别为三角形单元控制体对节点i、j、m的瓦斯体积分数贡献值。
3.2.3 采空区氧气浓度场平衡方程离散
采空区氧气浓度场平衡方程离散结果表示为
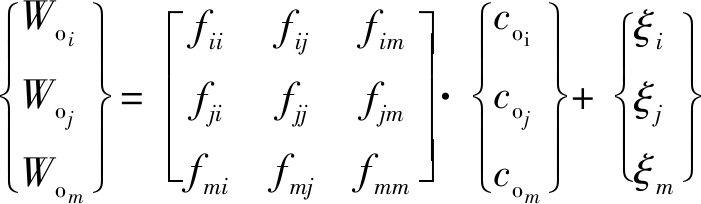
(9)
式中：
且
分别为关联的3个节点i、j、m的氧气体积分数；Woi、Woj、Wom分别为三角形单元控制体对节点i、j、m的氧气体积分数贡献值。
3.2.4 采空区固体温度场平衡方程离散
采空区固体温度场平衡方程离散表示为
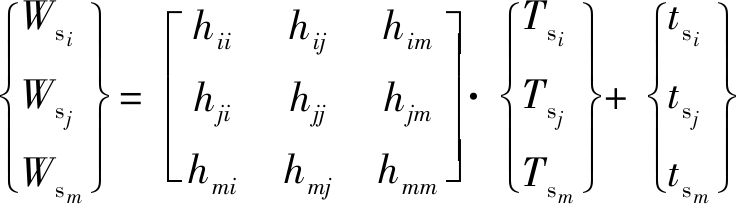
(10)
式中：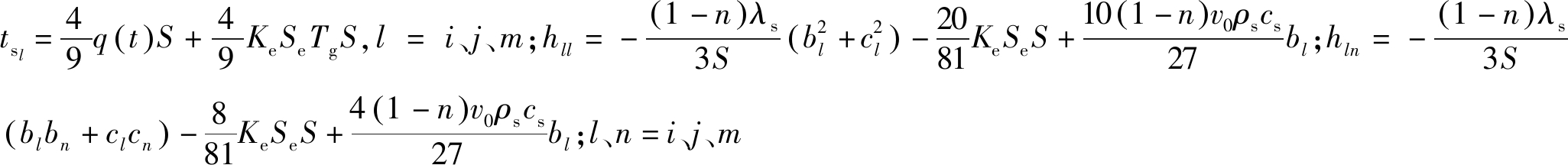
且l≠n；Tsi、Tsj、Tsm分别为关联的3个节点i、j、m的固体温度值；Wsi、Wsj、Wsm分别为三角形单元控制体对节点i、j、m的固体温度贡献值。
3.2.5 采空区气体温度场平衡方程离散
采空区气体温度场平衡方程离散表示为：
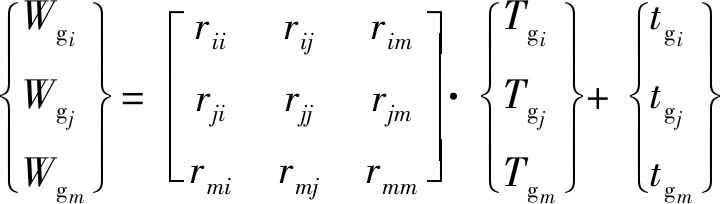
(11)
式中：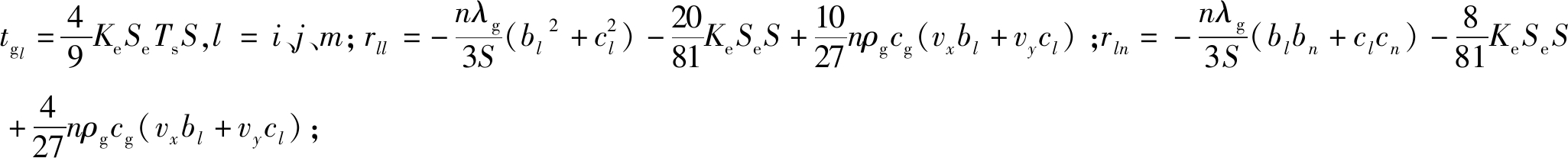
l、n=i、j、m且l≠n；Tgi、Tgj、Tgm分别为关联的3个节点i、j、m的气体温度值；Wgi、Wgj、Wgm分别为三角形单元控制体对节点i、j、m的气体温度贡献值。
4 程序解算结果
基于Microsoft Visual Basic平台编制数值模拟系统，建立的模型计算区域为采空区深度300 m，工作面长度200 m，工作面倾角0°，工作面通风阻力33.8 Pa，进风流温度20.0 ℃，回风流温度25.0 ℃，原始岩温23.1 ℃，推进速度设置为3.6 m/d，抽采负压(抽采口压力与采空区上隅角压力的差值)设置为-4 Pa，抽采点深度设置为30 m，计算模型的初始值及其他相关参数如下：
瓦斯密度/(kg·m-3)0.7168遗煤密度/(kg·m-3)1410单位面积瓦斯涌出量/(mol·m-1·s-1)0.0000287煤层原始压力/MPa1.5进、回风巷的压差/Pa15瓦斯扩散系数常数200氧气扩散影响系数150空气的动力黏性系数/(Pa·s)0.00001834空气的比热容/(J·kg-1·K-1)1010遗煤比热容/(J·kg-1·K-1)1200空气的导热系数/(W·m-1·K-1)0.0251煤的导热系数/(W·m-1·K-1)0.9对流换热系数/(W·m2·K-1)0.08温度耗氧速度系数a16.9381温度耗氧速度指数b10.0338温度放热强度系数e127.825温度放热强度指数f10.0316初始渗透率/m22×10-14
最后代入到程序中进行求解计算，利用Tecplot软件对求解结果进行可视化。
4.1 压力分布
采空区压力场的分布情况影响着漏风风流在采空区内的流动情况。设置好程序中的具体参数，求解可以得到进行瓦斯抽采前后的压力场分布情况，如图7所示。
图7 压力分布
Fig.7 Pressure distribution
由图7知，采空区气体压力的分布具有明显特征：在进行瓦斯抽采前，采空区下隅角处存在明显的气体高压区，气体压力从此处呈辐射状逐渐降低，在采空区深度方向上，其变化趋势较慢；采空区上隅角处存在明显的气体低压区，气体压力从此处呈辐射状逐渐升高，同样的，在采空区深度方向上，其变化趋势较慢。在进行瓦斯抽采后，气体高压区依旧存在于采空区下隅角处，而在抽采点处，由于抽采负压的存在，气体低压区在此处形成；气体压力从高压区呈辐射状向低压区逐渐降低，同样地在采空区深度方向上，气体压力变化趋势较慢。
4.2 瓦斯浓度分布
程序主要是对采空区瓦斯抽采的数值模拟，程序求解得到的瓦斯抽采后的瓦斯浓度场分布情况，如图8所示。由图8知，采空区瓦斯浓度的分布同样具有明显特征。
在进行瓦斯抽采前，采空区内瓦斯浓度的分布情况受采空区内漏风风流流动的影响。工作面进风巷新鲜风流从采空区下隅角流入采空区，带着一部分瓦斯从采空区上隅角流出采空区涌向工作面，造成采空区下隅角位置的瓦斯浓度较低，在采空区上隅角位置上瓦斯体积分数较高，达到7.0%，瓦斯浓度从下隅角位置向上隅角位置呈辐射状逐渐降低；由于采空区深处的垮落煤岩逐渐被压实，基本不存在流动风流，所以采空区深处的瓦斯体积分数高于近工作面的位置处，且瓦斯体积分数会随着采空区深度的增大而逐渐升高，最高达到16.0%。在进行瓦斯抽采后，采空区内漏风风流的流动会受到瓦斯抽采的影响，所以采空区瓦斯浓度的分布也出现相应的变化。采空区上隅角位置上的瓦斯浓度大幅降低，这说明从采空区上隅角流出采空区涌向工作面的瓦斯量大幅降低，大部分瓦斯被从抽采点位置抽出。因为采空区深处的垮落煤岩逐渐被压实，基本不存在流动风流，所以采空区深部的瓦斯体积分数受抽采的影响较小，但依旧高于采空区靠近工作面的位置处，且瓦斯体积分数会随着采空区深度的增大而逐渐升高，深部最大值降为13.0%。
图8 瓦斯浓度分布
Fig.8 Gas concentration distribution
4.3 氧气浓度分布
图9 氧气浓度分布
Fig.9 Oxygen concentration distribution
程序求解得到的进行瓦斯抽采前后的氧浓度场分布情况，如图9所示。由图9可知，采空区氧气浓度的分布同样具有明显特征：在瓦斯抽采前，采空区内氧气浓度的分布情况受采空区内漏风风流流动的影响。工作面进风巷新鲜风流携带着氧气从采空区下隅角流入采空区、从采空区上隅角流出采空区，所以在采空区下隅角位置上氧气浓度较高、在采空区上隅角位置上氧气浓度较低，氧气浓度从下隅角向上隅角呈辐射状逐渐降低；因为采空区深处的垮落煤岩逐渐被压实，基本不存在流动风流，所以采空区深处的氧气浓度会比采空区靠近工作面的位置处的氧气浓度低，且氧气浓度会随着采空区深度的增大而逐渐降低。在瓦斯抽采后，采空区内漏风风流的流动会受到瓦斯抽采的影响，所以采空区氧气浓度的分布也出现相应的变化。采空区浅部(0～100 m)各个位置的氧气浓度都有所升高，而采空区深部(100～300 m)各个位置的氧气浓度基本保持不变。这是因为采空区浅部的渗透率较大，抽采负压对采空区内漏风风流的流动的影响较明显；而采空区深部的冒落煤岩逐渐被压实，基本不存在流动风流，所以采空区深处的氧气浓度受抽采的影响较小。
4.4 固体温度分布
图10 固体温度分布
Fig.10 Solid temperature distribution
程序求解得到的进行瓦斯抽采前后的固体温度场分布情况，如图10所示。由图10知，采空区固体温度的分布同样具有明显特征：在瓦斯抽采前，进风巷新鲜风流从采空区下隅角流入采空区，采空区内遗煤与漏风风流中的氧气发生氧化反应放出大量热量。由图10可知，采空区下隅角位置比上隅角位置的氧气浓度高，加之采空区深部几乎无风流流动，采空区内遗煤放出的热量继续积聚形成高温区，固体温度向四周呈辐射状降低。在瓦斯抽采后，采空区内漏风风流的流动会受到瓦斯抽采的影响，采空区内氧气浓度的分布发生变化，最终导致采空区固体温度的分布也出现相应的变化。在瓦斯抽采的影响下，采空区内固体高温区的范围扩大，高温区的温度升高，从数值上看，采空区内各点的固体温度均比抽采前的固体温度高2 ℃。
4.5 气体温度分布
图11 气体温度分布
Fig.11 Air temperature distribution
程序求解得到瓦斯抽采前后的气体温度场分布情况，如图11所示。由图11可知，采空区气体温度的分布同样具有明显特征：在瓦斯抽采前，工作面进风巷新鲜风流从采空区下隅角流入采空区，采空区内遗煤会与漏风风流中的氧气发生氧化反应放出大量热量。而采空区内气体会与固体进行对流换热，所以采空区内气体温度的分布与固体温度的分布大致相似，都会形成高温区。气体温度由高温区向四周呈辐射状降低。在瓦斯抽采后，采空区内固体温度的分布出现相应的变化，这样采空区内气体温度的分布也会发生变化。在瓦斯抽采的影响下，采空区内气体高温区的范围扩大，高温区的温度升高，从数值上看，采空区内各点的气体温度均比抽采前的气体温度高2 ℃。
5 结 论
1)瓦斯抽采前，下隅角附近存在明显的气体高压区并且向四周逐渐降低，上隅角附近存在明显的气体低压区并且向四周逐渐升高，气体压力在采空区深度方向变化趋势缓慢；瓦斯抽采后，下隅角附近依旧存在气体高压区，而在抽采点处形成气体低压区，气体压力在采空区深度方向依旧变化趋势缓慢。
2)瓦斯抽采前，采空区下隅角附近的瓦斯浓度较低，采空区上隅角附近的瓦斯浓度较高，瓦斯浓度从下隅角向上隅角逐渐降低，采空区深处的瓦斯浓度会比采空区靠近工作面置处的瓦斯浓度高；瓦斯抽采后，采空区上隅角附近的瓦斯浓度大幅降低，而采空区深处的瓦斯受抽采的影响较小，浓度依旧高于采空区近工作面位置处。
3)瓦斯抽采前，采空区下隅角附近的氧气浓度较高，采空区上隅角附近的氧气浓度较低，氧气浓度从下隅角向上隅角逐渐降低，采空区深处的氧气浓度低于采空区靠近工作面位置处；瓦斯抽采后，采空区浅部(0～100 m)各个位置的氧气浓度都有所升高，而采空区深部(100～300 m)各个位置的氧气浓度基本保持不变。
4)瓦斯抽采前，在采空区漏入风侧存在明显的固体和气体高温区，并且温度由此处向四周逐渐降低；瓦斯抽采后，高温区依旧形成于采空区漏入风侧，但高温区的范围有所扩大，从数值上看，采空区内固体和气体温度最大值有所升高，要比抽采前高2 ℃。
[1] 孙继平,钱晓红.2004—2015年全国煤矿事故分析[J].工矿自动化,2016,42(11):1-5.
SUN Jiping,QIAN Xiaohong.Analysis of national coal mine accidents from 2004 to 2015[J].Industry and Automation,2016,42(11):1-5.
[2] 王旭昭,侯 磊,苏 龙.2011—2014年全国煤矿重特大事故统计分析与启示[J].中国公共安全(学术版),2015(2):26-29.
WANG Xuzhao,HOU Lei,SU Long.Statistical analysis and enlightenment of national coal mine heavy accidents in 2011-2014[J].China Public Safety(Academic Edition),2015(2):26-29.
[3] 安 宇,李 丹.2008—2014年我国煤矿事故统计分析及防治措施[J].煤矿现代化,2016(1):56-59.
AN Yu,LI Dan.Statistical analysis and prevention measures of coal mine accidents in China from 2008 to 2014[J].Modernization of Coal Mines,2016(1):56-59.
[4] 李 波,巨广刚,王 珂,等.2005—2014年我国煤矿灾害事故特征及规律研究[J].矿业安全与环保,2016,43(3):111-114.
LI Bo,JU Guanggang,WANG Ke,et al.Research on characteristics and laws of coal mine disaster accidents in China from 2005 to 2014[J].Mining Safety and Environmental Protection,2016,43(3):111-114.
[5] 朱红青,霍雨佳,方书昊,等.寺家庄矿综采工作面顶板走向高抽巷合理层位研究[J].煤炭科学技术,2021,49(1):234-239.
ZHU Hongqing,HUO Yujia,FANG Shuhao,et al.Research on the reasonable level of the high-drainage roadway with the roof strike of the fully mechanized mining face in Sijiazhuang Mine[J].Coal Science and Technology,2021,49(1):234-239.
[6] 康 雪.上隅角瓦斯治理及采空区漏风流场模拟研究[D].阜新:辽宁工程技术大学,2012.
[7] 刘彦青,孙永新,赵 灿,等.采空区密闭联络巷埋管抽采瓦斯技术参数优化及应用[J].煤炭科学技术,2020,48(12):131-140.
LIU Yanqing,SUN Yongxin,ZHAO Can,et al.Optimization and application of technical parameters for gas drainage with buried pipes in closed connected roads in goafs[J].Coal Science and Technology,2020,48(12):131-140.
[8] 孟 然,徐经苍,魏攀登.顺层瓦斯抽放钻孔渗流场数值模拟及应用[J].西安科技大学学报,2015,35(5):561-566.
MENG Ran,XU Jingcang,WEI Pandeng.Numerical simulation and application of seepage field in gas drainage of bedding gas[J].Journal of Xi′an University of Science and Technology,2015,35(5):561-566.
[9] 程卫民,张孝强,王 刚,等.综放采空区瓦斯与遗煤自然耦合灾害危险区域重建技术[J].煤炭学报,2016,41(3):662-671.
CHENG Weimin,ZHANG Xiaoqiang,WANG Gang,et al.Reconstruction technology of natural coupled disaster hazard area in gas and coal mining areas in fully mechanized caving face[J].Journal of China Coal Society,2016,41(3):662-671.
[10] 毕慧杰,邓志刚,赵善坤,等.高瓦斯综采工作面定向高位钻孔瓦斯抽采技术研究[J].煤炭科学技术,2019,47(4):134-140.
BI Huijie,DENG Zhigang,ZHAO Shankun,et al.Research on directional high-location borehole gas drainage technology in high gas fully mechanized mining face[J].Coal Science and Technology,2019,47(4):134-140.
[11] 刘 军,周东平,黄旭超,等.急倾斜特厚煤层分段开采卸压瓦斯抽采技术[J].煤炭科学技术,2020,48(4):206-210.
LIU Jun,ZHOU Dongping,HUANG Xuchao,et al.Pressure-relief gas drainage technology for section mining in steeply inclined and extra-thick coal seams[J].Coal Science and Technology,2020,48(4):206-210.
[12] 闫保永,曹 柳,张家贵.煤层顶板裂隙带瓦斯抽采技术与装备探索[J].煤炭科学技术,2020,48(10):60-66.
YAN Baoyong,CAO Liu,ZHANG Jiagui.Exploration of gas drainage technology and equipment in the cracked zone of coal roof[J].Coal Science and Technology,2020,48(10):60-66.
[13] 周连春.低透气性高瓦斯矿井瓦斯抽放参数优化研究[D].包头:内蒙古科技大学,2011.
[14] 方前程,王兆丰,王 林.高瓦斯厚煤层综放工作面采空区瓦斯抽放的研究[J].煤炭工程,2007(9):77-79.
FANG Qiancheng,WANG Zhaofeng,WANG Lin.Study on gas drainage in goaf of fully mechanized caving face in high gas thick coal seam[J].Coal Engineering,2007(9):77-79.
[15] 周加川.采空区瓦斯抽放技术的研究与应用[D].太原:太原理工大学,2012.
[16] 章梦涛,王景琰.采场空气流动状况的数学模型和数值方法[J].煤炭学报,1983(3):48-56.
ZHANG Mengtao,WANG Jingyan.Mathematical model and numerical method for air flow in stope[J].Journal of China Coal Society,1983(3):48-56.
[17] 李宗翔,纪书丽,题正义.采空区瓦斯与大气两相混溶扩散模型及其求解[J].岩石力学与工程学报,2004,24(16):2971-2976.
LI Zongxiang,JI Shuli,TI Zhengyi.The two-phase miscible diffusion model of gas and atmosphere in goaf and its solution[J].Chinese Journal of Rock Mechanics and Engineering,2004,24(16):2971-2976.
[18] 李宗翔,孟宪臣,赵国忱.任意形冒落非均质采空区流场流态数值模拟[J].力学与实践,2005,27(6):26-28.
LI Zongxiang,MENG Xianchen,ZHAO Guochen.Numerical simulation of flow pattern of arbitrary caving heterogeneous in goaf[J].Mechanics in Engineering,2005,27(6):26-28.
[19] 李宗翔,许端平,刘立群.采空区自然发火“三带”划分的数值模拟[J].辽宁工程技术大学学报(自然科学版),2002(5):545-548.
LI Zongxiang,XU Duanping,LIU Liqun.Numerical simulation of the“three belts”division of natural ignition in goaf[J].Journal of Liaoning Technical University(Natural Science Edition),2002(5):545-548.
[20] 李宗翔,吴志君,王振祥.采空区遗煤自燃升温过程的数值模型及其应用[J].安全与环境学报,2004,4(6):58-61.
LI Zongxiang,WU Zhijun,WANG Zhenxiang.Numerical model and application of self-ignition heating process of coal in goaf[J].Journal of Safety and Environment,2004,4(6):58-61.
[21] 王 真,陈长华,杨 羽.采空区气体流动状态与渗流模型[J].煤矿安全,2009,40(11):98-101.
WANG Zhen,CHEN Changhua,YANG Yu.Gas flow state and seepage model in goaf[J].Safety in Coal Mines,2009,40(11):98-101.
[22] 李新华,许家林,汪 锋,等.工作面宽度对采动裂隙“O”形圈发育形态的影响规律[J].煤矿安全,2012,43(9):34-36.
LI Xinhua,XU Jialin,WANG Feng,et al.Effect of working face width on the developmental morphology of mining O-rings[J].Safety in Coal Mines,2012,43(9):34-36.
[23] 彭 冬.王家岭矿上隅角瓦斯治理机制及定向钻孔关键设计参数研究[D].北京:煤炭科学研究总院,2019.
[24] 许家林,孟广石.应用上覆岩层采动裂隙“O”形圈特征抽放采空区瓦斯[J].煤矿安全,1995,26(7):2-4.
XU Jialin,MENG Guangshi.Application of the o-rings feature of the mining overlying strata to pump gas in the goaf[J].Coal Mine Safety,1995,26(7):2-4.
[25] 钱鸣高,许家林.覆岩采动裂隙分布的“O”形圈特征研究[J].煤炭学报,1998,23(5):466-469.
QIAN Minggao,XU Jialin.Study on the characteristics of O-rings in the fracture distribution of overburden mining[J].Journal of China Coal Society,1998,23(5):466-469.
