0 引 言
地下工程中,岩柱或煤柱作为主要支承结构在地下煤矿开采和金属矿床开采等工程中广泛存在。无论是长期永久使用还是短期临时使用,岩柱或煤柱都要有足够的稳定性,否则岩柱发生破坏可能会造成十分严重的后果[1-2]。地下空间开挖打破原有应力平衡状态,将原有三向受力状态转为二向甚至单向受力状态,应力转移到相邻支承结构,导致地下空间结构中局部地方出现应力集中、大变形、甚至垮塌现象,围岩结构稳定性显著降低[3-4]。因此,岩柱强度问题直接关系到岩柱稳定性,关系到地下空间工程安全。地下空间环境复杂,岩柱强度受到多种因素影响,包括岩柱尺寸、岩体岩性、岩体中节理裂隙分布特征等因素。由于所受影响因素复杂,目前尚未有确定岩柱强度的统一标准与方法。在工程实践中,一般采用经验类比法和简化条件下的理论分析[5-6]。经验类比法是以实际工程为背景,考虑岩柱形状、尺寸和不连续等特性,基于岩样实验室岩石物理力学试验估算的强度。常用经验类比法包括形状影响经验公式法、尺寸影响经验公式法、经验岩体强度破坏准则和结构不连续经验分析。理论分析多以弹塑性理论为基础,认为岩柱从边缘到核心是由塑性屈服区向弹性区过渡的,承载能力从外向内逐渐增大。虽然这2种方法为实际工程解决了很多问题,但均不能详细地考虑具体实际工况,不能很好地预测岩柱的破坏强度及破坏形式。随着计算机技术发展,数值模拟技术在解决工程实际复杂问题中应用越来越广泛。对于岩柱破坏强度和破坏形式的研究,常用的数值模拟方法是离散元法,该方法最早由CUNDALL[7]提出:该方法将岩体视为由节理分割形成的离散块体组合,并通过接触相互连接,每个块体服从牛顿第二定律。近年来,在传统离散元基础上,POTYONDY[8]提出黏结颗粒模型(Bonded particle model),成功模拟岩石多种力学特征,包括变形、开裂、膨胀和声发射等。在此基础之上,合成岩体模型技术(Synthetic Rock Mass,SRM)[9]被提出并用以构造岩体结构模型,解决实际工程复杂问题。周喻等[10]基于等效岩体技术分析了断续双节理岩石试件破裂机制,并结合室内试验研究成果,验证了等效岩体技术在断续节理岩体力学特性研究中的适宜性和可靠性;朱万成等[11]从节理岩体表征单元体的力学意义出发,研究了节理岩体参数确定方法,得出节理岩体表征单元尺寸(Representative Elementary Volume,REV)及其影响因素;王培涛等[12]研究了应用于颗粒流的节理边坡岩体强度参数获取方法和挂帮矿回采中岩体变形、失稳、破坏过程,得到的岩体破坏模式与现场勘测结果以及相似试验结果相似。但以往研究较少涉及岩柱稳定性,基于此,针对裂隙分布特征对岩柱稳定性影响问题,阐述合成岩体模型、建模方法和微观参数的选择与标定,通过模拟结果分析岩体中裂隙密度和裂隙倾角对岩柱破坏强度及破坏形式的影响,为岩柱稳定性分析提供思路和方法。
1 合成岩体模型
合成岩体模型是由IVARS等[9]提出的数值模拟技术,主要包含离散元(Discrete Element Model,DEM)和节理网络模型(Discrete Fracture Network,DFN)2种模拟方法。复杂结构岩体可通过黏结颗粒模型(使用平直节理黏结模型)、节理模型(采用光滑节理模型)和节理网络模型(DFN)模拟岩块、裂隙以及节理网络。
1.1 平直节理黏结模型
颗粒流离散元模型由一系列直径不同的刚性颗粒组成,通过颗粒与颗粒间接触的相互作用来模拟颗粒流介质力学特性。颗粒间接触的相互作用服从初始设置的本构模型。目前模拟岩石最常用的接触类型有3种:接触黏结模型(Contact-Bonded Model,CBM)、平行黏结模型(Parallel-Bonded Model,PBM)和平直节理黏结模型(Flat-Joint-Bonded Model,FJBN)。以往研究[8,11]表明前2种接触模型较难得到合理的压拉强度比,而平直节理黏结模型能够较好解决这个问题,除此之外,还能更好地模拟岩石的微观结构(图1)。因此,宜采用平直节理黏结模型模拟岩块。

图1 岩石的微观结构
Fig.1 Rock microstructure
典型的二维平直节理黏结接触模型包含刚性球和接触(图2)。不同于接触黏结模型和平行黏结模型,平直节理黏结模型的接触可以分割成均长黏结的子接触和未黏结的子接触[13-16]。这2种接触服从不同的本构关系,在黏结接触中,其剪切力服从摩尔-库伦准则:
τe=c+σetan φ
(1)
其中:σe和τe分别为黏结接触法向和切向应力;c、φ分别为黏结的黏聚力、内摩擦角。黏结接触受力大于剪切强度或者抗拉强度时,子接触破坏形成微裂隙。
在未黏结接触中,其剪切力服从库伦摩擦准则:
τe=σetan φr
(2)
式中:φr为残余摩擦角。

μ′—颗粒间切向摩擦因数;σt—黏结的抗拉强度; gc—颗粒表面最小间距,用于判断是否接触
图2 平直节理黏结模型
Fig.2 Flat joint model
1.2 光滑节理模型
为模拟裂隙力学性质及其破坏行为,文献[7]提出了光滑节理模型。当光滑节理模型嵌入黏结模型时,平直节理黏结模型将会被光滑节理模型代替,周围被赋予光滑节理模型的球体的力学行为不再受颗粒黏结接触方向影响。2个相邻颗粒不发生沿颗粒表面的绕行行为,只发生相对滑动,从而模拟裂隙的力学行为(图3)。

![]() 节理单位法向向量;
节理单位法向向量;![]() 节理单位切向向量;
节理单位切向向量;![]() 光滑节理接触法向量;θp—节理倾角;
光滑节理接触法向量;θp—节理倾角;![]() 两颗粒平均半径
两颗粒平均半径
图3 光滑节理模型
Fig.3 Smooth joint model
1.3 裂隙网络模型
成岩作用和长期地质作用下,岩体中通常存在大量随机裂隙。裂隙网络模拟技术基于蒙特卡洛方法,认为裂隙参数(长度、倾角、密度、位置等)服从某种随机分布的随机变量,通过计算机模拟生成相关随机数,进而生成相应随机裂隙,典型的裂隙分布函数有均匀分布、负指数分布、正态分布、对数分布[17-18]。这些方法生成随机网络裂隙一般包括裂隙中心点坐标、裂隙倾角以及裂隙迹长的确定。
1)裂隙中心点坐标的确定。以往研究表明裂隙中心坐标服从均匀分布,即裂隙中心点坐标(x0,y0)以相同概率出现在研究区域内。假设研究区域为边长为l的正方形,R1和R2为服从(0,1)均匀分布的随机数,则中心点坐标可以通过式(3)、式(4)获得
x0=lR1
(3)
y0=lR2
(4)
2)裂隙倾角的确定。在二维应用过程中,裂隙倾角θ服从可以通过包装正态分布(wrapped normal distribution)和冯·米塞斯分布模拟。包装正态分布函数如下:
(5)
式中:μ为裂隙的平均角度;σ为倾角的标准差。
冯·米塞斯分布如下:
f(θ)=ekcos(θ-μ)/[2πI0(k)]
(6)
式中:I0(k)为贝叶斯公式;k为方位角集中程度。
3)裂隙迹长的确定。现场研究表明,裂隙的迹长L服从负指数分布和幂律分布。假设迹长服从负指数分布,迹长均长为u,则裂隙迹长见式(7)。
L=-uln(1-R)
(7)
式中:R为服从(0,1)均匀分布的随机数。
2 合成岩体模型建立
离散元模型细观参数与模型宏观力学性质没有直接关系,需通过标定过程来确定与宏观力学性质对应的细观力学参数。此过程通常采用数值模拟试验(单轴抗压、单轴抗拉或者劈裂试验等)来建立彼此间关系。以陕西西王寨煤矿为研究背景,地质勘探表明岩体完整性差,内、外生裂隙较发育,有必要研究裂隙对岩柱稳定性影响。以灰岩为研究对象,其力学性质见表1。
表1 宏观力学参数
Table 1 Macro-mechanical parameters
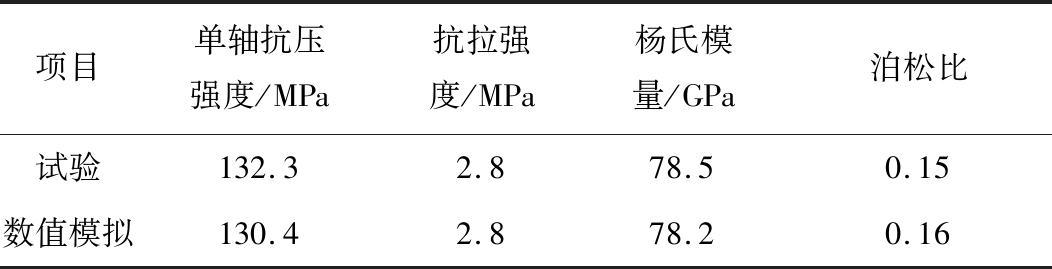
项目单轴抗压强度/MPa抗拉强度/MPa杨氏模量/GPa泊松比试验132.32.878.50.15数值模拟130.42.878.20.16
2.1 平直节理黏结模型
采用单轴抗压和单轴抗拉试验标定岩体宏观力学参数(单轴抗压强度、抗拉强度、杨氏模量和泊松比),即用数值模拟得到的宏观力学参数去匹配实验室所得的相应力学参数。如图4所示,试件宽度50 mm,高100 mm。试件上下两端为刚性墙体,模拟加载压盘,单轴抗压加载过程中,底压盘保持不动,而上压盘以一定速度向下移动,直至试件破坏,加载过程记录试件应力-应变关系,以获取试件力学参数(单轴抗压强度、杨氏模量和泊松比)。单轴抗拉试验中,定义上下两端的部分球体为端部,在抗拉过程中,端部分别以一定速度向外侧拉,从而获取抗拉强度。
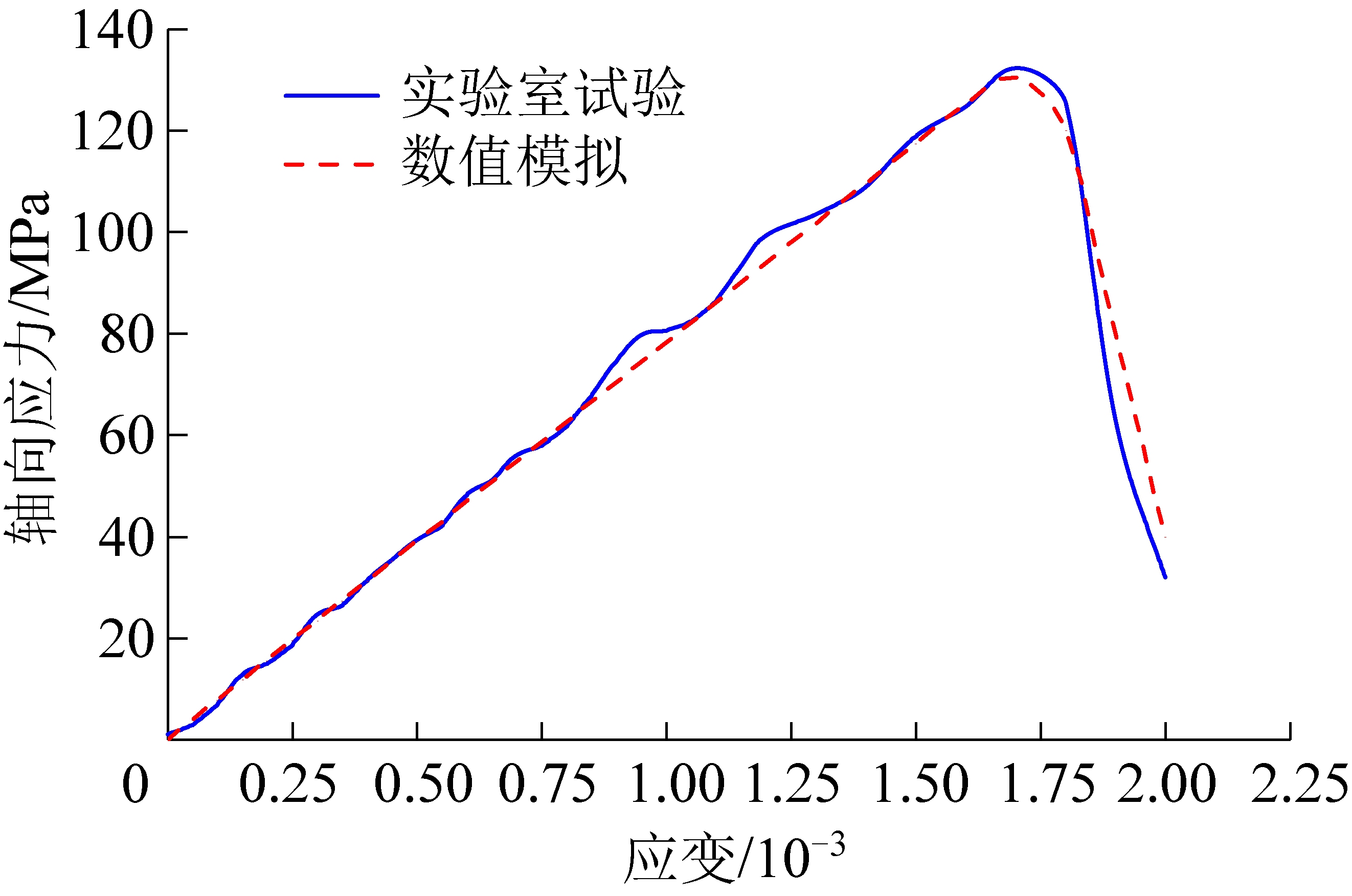
图4 岩石单轴压缩实验室结果和数值模拟结果
Fig.4 Uniaxial compression tests of intact rock from experimental and numerical results
标定PFC模型的力学参数与试验结果对比见表2,误差基本小于1%,标定的符合宏观岩体特性的颗粒流细观力学参数见表2。另外,实验室和数值模拟单轴压缩应力-应变曲线对比(图4)表明:数值模拟结果高度吻合实验室试验结果,可应用于下一步数值建模分析。
表2 合成岩体模型细观力学参数
Table 2 Micro-parameters of SRM model
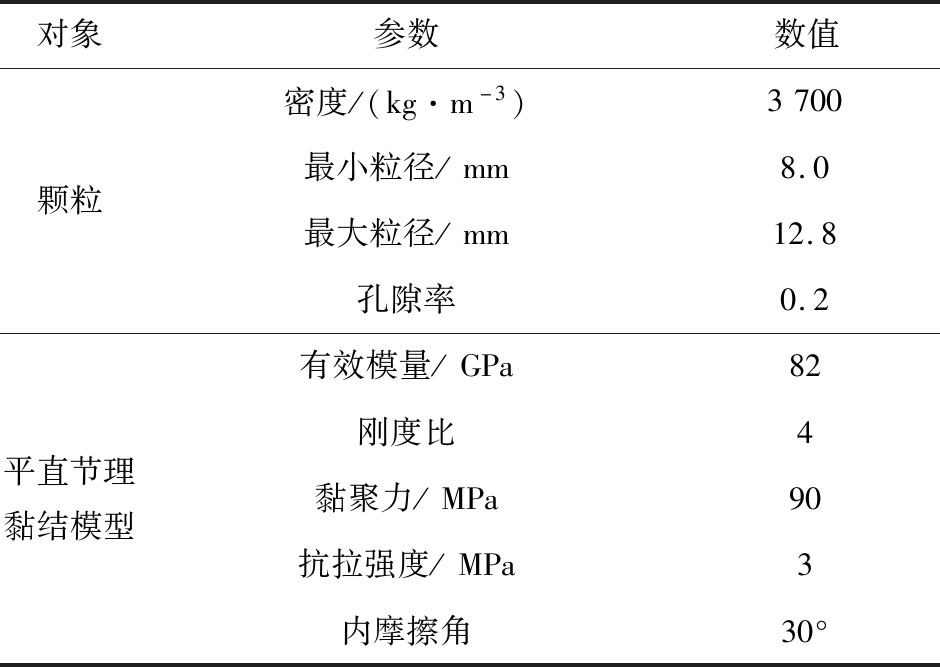
对象参数数值颗粒密度/(kg·m-3)3700最小粒径/mm8.0最大粒径/mm12.8孔隙率0.2平直节理黏结模型有效模量/GPa82刚度比4黏聚力/MPa90抗拉强度/MPa3内摩擦角30°
2.2 光滑节理模型参数
完整岩块力学参数标定后,加入光滑节理模型,可模拟裂隙岩体。采用试错方法,标定光滑节理模型力学参数。光滑节理微观力学参数如下:法向刚度200 GPa/m,切向刚度100 GPa/m,黏聚力0.5 MPa,内摩擦角30°。
2.3 建立合成岩体模型
岩体合成模型技术如图5所示,将裂隙网络模型建立的裂隙网络嵌入由平直节理黏结模型建立的岩石模型中,并将光滑节理模型的参数赋予裂隙,从而建立起岩体模型[19]。

图5 合成岩体模型
Fig.5 Synthetic rock mass model
岩柱模型相对于实验室岩样较大,需要颗粒数目较多,采用连续-非连续周期边界技术建立平直节理黏结模型,以降低模型生成时间。
3 模拟结果
采用2 m(直径)×4 m(高度)岩柱模型研究裂隙密度和裂隙倾角对岩柱强度的影响,模拟过程和结果分析如下。
3.1 裂隙密度对岩柱强度的影响
为研究裂隙密度对岩柱强度的影响,采取控制变量法,即裂隙的其他参数保持不变,裂隙位置和裂隙倾角采用均匀分布,裂隙长度采用幂次分布。图6为裂隙密度P21(单位面积内累计裂缝长度)由1.0 m/m2增加至5.0 m/m2的合成岩体岩柱模型。

图6 不同裂隙密度的合成岩体岩柱模型
Fig.6 Composite rock pillar models with different fracture density
为更好反映裂隙随机性和不确定性,裂隙网络随机因子设置8次,获取相同参数条件下不同裂隙结构,然后将岩柱模型进行单轴加载获取岩柱单轴抗压强度。不同裂隙密度条件下,单轴抗压强度和变形模量随裂隙密度增强而减弱。如图7所示,由于裂隙结构不确定性和随机性,裂隙密度相同的条件下单轴抗压强度和变形模量在一定区间内波动,其平均值与裂隙密度呈负相关,因而裂隙的存在可显著降低岩柱强度。

图7 裂隙密度P21对岩柱抗压强度和变形模量的影响
Fig.7 Effect of fracture density P21 on compressive strength and deformation modulus of rock pillars
裂隙密度P21由1 m/m2增加至5 m/m2过程中,岩柱平均强度由103.5 MPa 降低至69.5 MPa,岩柱平均强度降低34.0 MPa,岩柱平均变形模量由66.7 GPa降低至45.7 GPa。岩柱破坏形式也受裂隙密度影响,如图8所示,裂隙密度较小时,岩柱易形成“X”形压剪破坏,并且形成较小的破坏块体;随裂隙密度增大,“X”形压剪破坏逐渐消失,并形成较大的破坏块体。此外,如图9所示,随裂隙密度增大,外界作用力产生的微裂隙反而减小。这种现象是由于在裂隙较多的情况下,更容易使本身具有的裂隙相互贯通,形成破坏,而裂隙较少时,岩柱的岩块部分更容易发生破坏,形成小块体和微裂隙。

图8 裂隙密度对岩柱破坏形式的影响
Fig.8 Effect of fracture density on failure modes of rock pillars

图9 裂隙密度对微裂隙的影响
Fig.9 Effect of fracture density on micro-fractures
3.2 裂隙倾角对岩柱强度的影响
类似的,研究裂隙倾角对岩柱强度影响过程中,其他参数保持不变,裂隙密度P21设置为3 m/m2,裂隙位置采用均匀分布,裂隙长度采用幂次分布,裂隙倾角由0°增加至90°。不同角度、相同裂隙网络参数条件下,生成8个随机模型如图10所示。
裂隙角度小于裂隙摩擦角时,裂隙的存在对岩柱强度没有影响,如图11所示。裂隙角度大于裂隙摩擦角时,岩柱强度随倾角增加而降低,裂隙角度为60°时,达到最小值,然后随裂隙角度增加而降低;裂隙角度与加载方向一致时,岩柱强度又重新达到最大值;岩柱变形模量随裂隙倾角增加而逐渐增加。
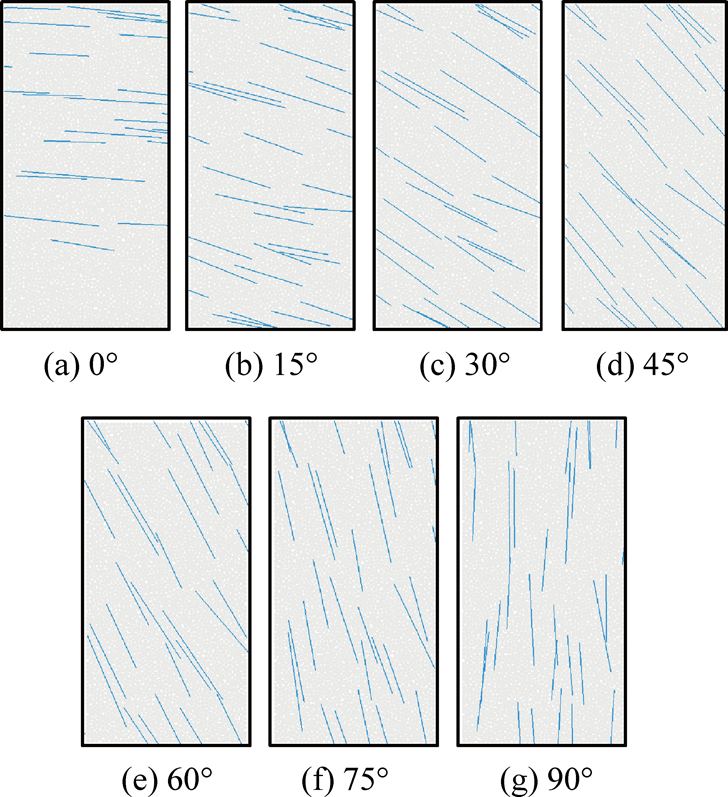
图10 裂隙不同倾角的合成岩体岩柱模型
Fig.10 Composite rock pillar models with different dip angles
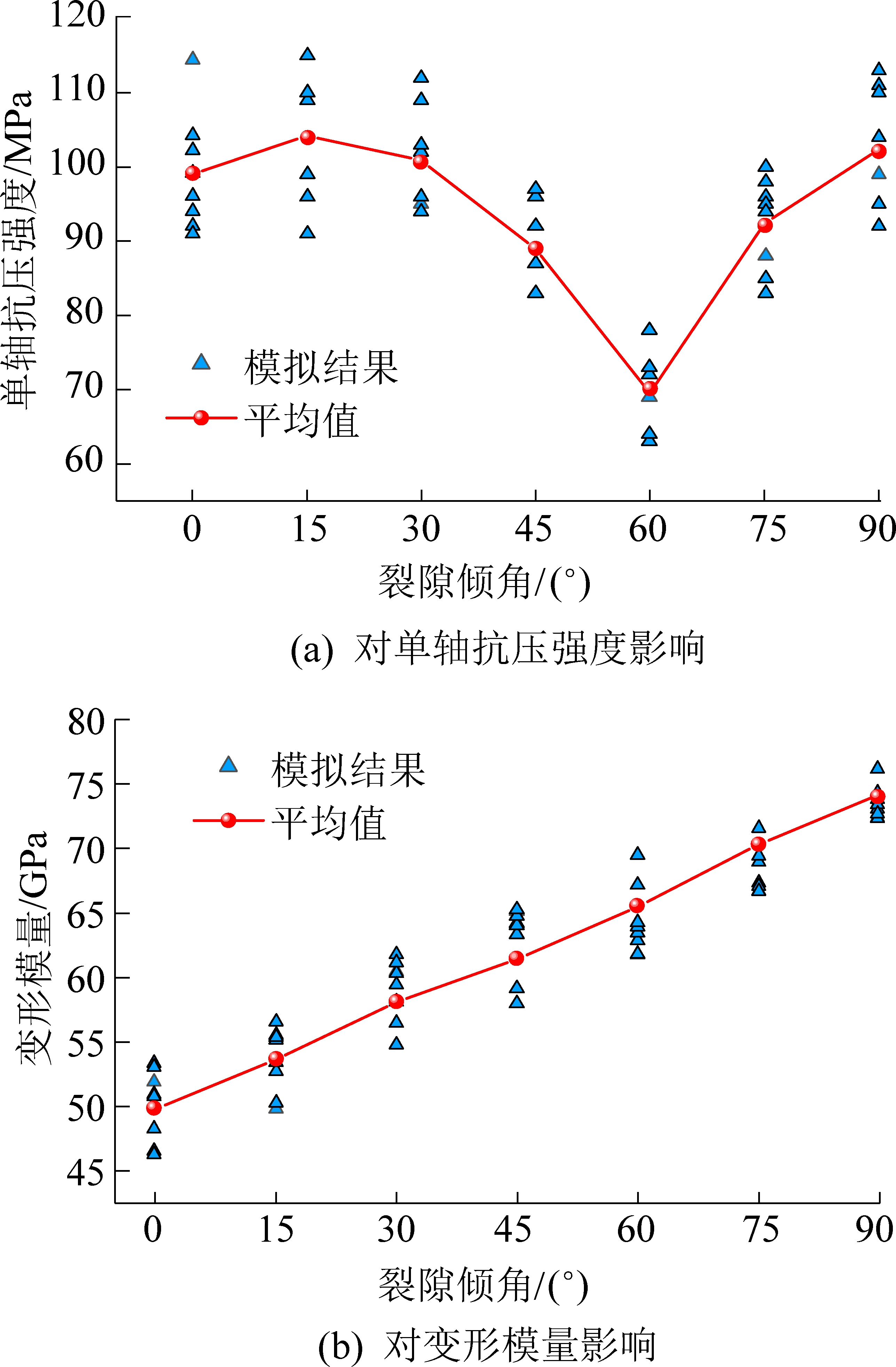
图11 裂隙倾角对岩柱抗压强度和变形模量的影响
Fig.11 Effect of joint orientation on compressive strength and deformation modulus of rock pillars
岩柱破坏形式也受裂隙密度影响,如图12所示,裂隙倾角小于临界角φ时,岩柱破坏形式成“X”形压剪破坏,形成较小的破坏块体;随裂隙倾角增大至45°和60°,岩柱“X”形破坏逐渐消失,并形成剪切滑移破坏,形成的破坏块体较大;随裂隙倾角继续增大至大于45°+φ/2时,岩柱破坏形式又重新形成“X”形破坏,形成较小的破坏块体。另一方面,如图13所示,微裂隙数量也随裂隙角度成“U”形变化。裂隙倾角大于临界角度时,原裂隙端部更容易产生翼型张拉微裂隙,更容易发生贯通,形成破坏。
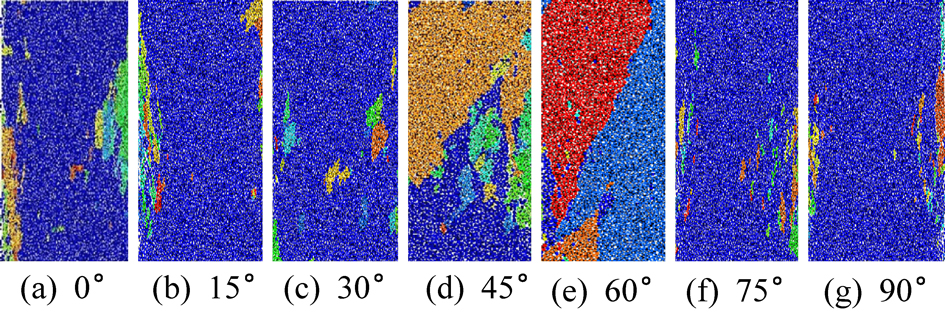
图12 裂隙倾角对岩柱破坏形式的影响
Fig.12 Effect of fracture dip on failure mode of rock pillars
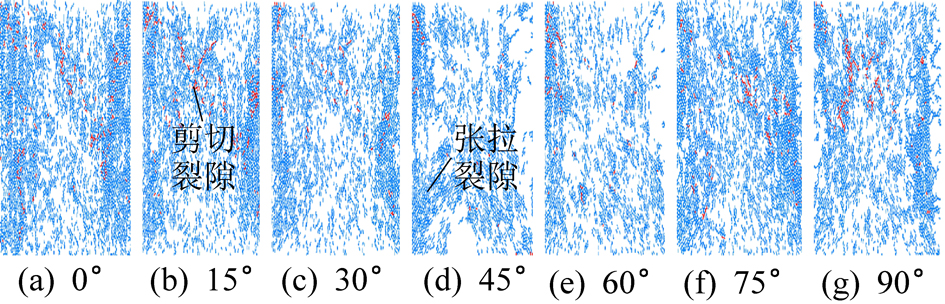
图13 裂隙倾角对微裂隙的影响
Fig.13 Effect of fracture dip on micro-fractures
4 结 论
1)通过节理网络模型和离散元构建合成岩柱模型,研究裂隙参数对岩柱强度的影响,可为确定岩柱强度提供思路。
2)岩柱强度随裂隙密度P21增加而降低。裂隙密度较小时,岩柱成“X”形压剪破坏;裂隙密度较大时,岩柱“X”形压剪破坏逐渐消失;岩柱产生的微裂隙与裂隙密度成负相关。
3)岩柱强度和微裂隙随裂隙倾角变化(0°到90°)而呈“U”形变化,裂隙倾角为0°和90°时达到最大值,在60°达到最小值;岩柱变形模量随裂隙倾角增加而增加;裂隙倾角小于φ或大于45°+φ/2时,岩柱易形成“X”形压剪破坏,而裂隙倾角介于φ与45°+φ/2之间时,岩柱易形成剪切滑移破坏。
[1] 孙广忠.岩体结构力学[M].北京:科学出版社,1988.
[2] 焦建康,鞠文君,吴拥政,等.动载冲击地压巷道围岩稳定性多层次控制技术[J].煤炭科学技术,2019,47(12):10-17.
JIAO Jiankang,JU Wenjun,WU Yongzheng,et al.Multi-layer control technologies for surrounding rock stability of dynamic-loading rock burst roadway[J].Coal Science and Technology,2019,47(12):10-17.
[3] 石 崇,杨文坤,沈俊良,等.动压巷道区段煤柱合理留设宽度研究[J].煤炭科学技术,2019,47(7):108-114.
SHI Chong,YANG Wenkun,SHEN Junliang,et al.Study on reasonable width of coal pillar in dynamic pressure roadway[J].Coal Science and Technology,2019,47(7):108-114.
[4] 杨军辉,蒋再胜,谢生荣.深部大断面巷道交叉点围岩稳定性分析及控制技术[J].煤炭科学技术,2020,48(6):49-56.
YANG Junhui,JIANG Zaisheng,XIE Shengrong.Stability analysis and control technology of surrounding rocks at deep large cross-section roadway[J].Coal Science and Technology,2020,48(6):49-56.
[5] 尹升华,吴爱祥,李希雯.矿柱稳定性影响因素敏感性正交极差分析[J].煤炭学报,2012,37(S1):48-52.
YIN Shenghua,WU Aixiang,LI Xiwen.Orthogonal polar difference analysis for sensitivity of the factors influencing the ore pillar stability[J].Journal of China Coal Society,2012,37(S1):48-52.
[6] 周晓明,刘长武,王 东,等.岩柱应力分布规律及其稳定性分析[J].铜业工程,2011(3):1-6.
ZHOU Xiaoming,LIU Changwu,WANG Dong,et al.Distribution and stability analysis of rock pillar stress[J].Copper Engineering,2011(3):1-6.
[7] CUNDALL P A.A computer model for simulating progressive,large-scale movement in blocky rock system[A].Proceedings of the Symposium of the International Society for Rock Mechanics,Society for Rock Mechanics(ISRM),1971,II-8,France.
[8] POTYONDY D O.The bonded-particle model as a tool for rock mechanics research and application:current trends and future directions[J].Geosystem Engineering,2015,18(1):1-28.
[9] IVARS D M,PIERCE M E,DARCEL C,et al.The synthetic rock mass approach for jointed rock mass modelling[J].International Journal of Rock Mechanics and Mining Sciences,2011,48(2):219-244.
[10] 周 喻,吴顺川,王 莉,等.等效岩体技术在断续双节理岩石试件破裂机制细观分析中的应用[J].岩土力学,2013,34(10):2801-2809.
ZHOU Yu,WU Shunchuan,WANG Li,et al.Distribution and stability analysis of rock pillar stress[J].Rock and Soil Mechanics,2013,34(10):2801-2809.
[11] 朱万成,张敏思,张洪训,等.节理岩体表征单元体尺寸确定的数值模拟[J].岩土工程学报,2013,35(6):1121-1127.
ZHU Wancheng,ZHANG Minsi,ZHANG Hongxun,et al.Numerical simulation for determining the size of representative element volume(REV)of jointed rock mass[J].Chinese Journal of Geotechnical Engineering,2013,35(6):1121-1127.
[12] 王培涛,杨天鸿,于庆磊,等.节理边坡岩体参数获取与PFC2D应用研究[J].采矿与安全工程学报,2013,30(4):560-565.
WANG Peitao,YANG Tianhong,YU Qinglei,et al.On obtaining jointed rock slope geo-parameters and the application of PFC2D[J].Journal of Mining &Safety Engineering,2013,30(4):560-565.
[13] 张学朋,王 刚,蒋宇静,等.基于颗粒离散元模型的花岗岩压缩试验模拟研究[J].岩土力学,2014,35(S1):99-105.
ZHANG Xuepeng,WANG Gang,JIANG Yujing,et al.Simulation research on granite compression test based on particle discrete element model[J].Rock and Soil Mechanics,2014,35(S1):99-105.
[14] WU Shunchuan,XU Xueliang.A Study of three intrinsic probl-ems of the classic discrete element method using flat-joint model[J].Rock Mechanics and Rock Engineering,2016,49(5):1813-1830.
[15] CASTRO-FILGUEIRA U,ALEJANO L R,![]() J,et al.Sensi-tivity analysis of the micro-parameters used in a PFC analysis towards the mechanical properties of rocks[J].Procedia Engineering,2017,191:488-495.
J,et al.Sensi-tivity analysis of the micro-parameters used in a PFC analysis towards the mechanical properties of rocks[J].Procedia Engineering,2017,191:488-495.
[16] DE SILVA V R S,RANJITH P G,PERERA M S A,et al.A low energy rock fragmentation technique for in-situ leaching[J].Journal of Cleaner Production,2018,204:586-606.
[17] LISJAK A,GRASSELLI G.A review of discrete modeling techniques for fracturing processes in discontinuous rock masses[J].Journal of Rock Mechanics and Geotechnical Engineering,2014,6(4):301-314.
[18] 刘富有,陈鹏宇,余宏明.基于Flatjoint接触模型的岩石单轴压缩和巴西劈裂颗粒流模拟研究[J].长江科学院院报,2016,33(9):60-65.
LIU Fuyou,CHEN Pengyu,YU Hongming.PFC simulation of uniaxial compression and Brazilian splitting test of rock based on Flat-jointed bonded-particle material[J].Journal of Yangtze River Scientific Research Institute,2016,33(9):60-65.
[19] 许永祥,王国法,李明忠,等.基于黏结颗粒模型的特厚坚硬煤综放开采数值模拟研究[J].煤炭学报,2019,44(11):3317-3328.
XU Yongxiang,WANG Guofa,LI Mingzhong,et al.Numerical simulation of longwall top-coal caving with extra-thick and hard coal seam based on bonded particle model[J].Journal of China Coal Society,2019,44(11):3317-3328.
