0 引 言
西北矿区煤炭资源储量丰富,可采煤层数量多,且层间距较小。由于早期开采技术相对落后,上组煤层多采用房式开采,遗留大面积房式采空区,据统计,仅鄂尔多斯境内的房式采空区面积就达307.61 km2[1]。房式采空区的独特性在于其上覆岩层自重均由遗留煤柱群来承担,煤柱的稳定性决定了整个采空区的稳定状态。下组煤层开采过程中,煤柱上方应力重新分布,造成煤柱的最大主应力增大,当上覆载荷大于煤柱极限强度时,煤柱塑性破坏区将由四周逐渐向中心扩展,直至发生整体塑性破坏从而失去支撑顶板的能力[2],此过程易诱发煤层顶板联动垮落形成强矿压致灾[3]。因此,评价房式煤柱稳定性对下组煤层群安全开采具有重要的意义。房式采煤法是柱式采煤法的一种,在煤层每隔一定距离开采煤房,煤房之间留有一定宽度的煤柱支撑顶板,煤房及煤柱的尺寸设计取决于采高、埋深、煤层顶底板力学特性等[4]。房、柱分布规律分为平行分布(棋盘形)、“品”字形分布两类,煤柱为采空区内的唯一承载结构[5-6]。影响房式采空区煤柱稳定性的因素主要有煤柱分布方式、上覆载荷及力学、几何特性参数等[7]。Voronoi图法、模糊理论、重整化群理论广泛应用于不规则房式煤柱群、条带煤柱、非煤矿柱的稳定性研究中[8-10],认为影响煤柱群失稳的主要因素为柱群的分布形式、各柱体间尺寸及强度的均匀性。为具体研究煤柱群中某一煤柱失稳破坏特征,基于煤柱群稳定性的研究基础,结合煤柱上覆载荷分布及传递特性发展出了概率逼近法、逻辑回归法及蒙特卡洛法等数理统计方法[11-13],这类方法考虑了煤柱尺寸及力学参数的不确定性及其他因素,在房式煤柱的稳定性评估中应用广泛。随后尖点突变失稳模型将拓扑学、奇点理论等非线性理论引入到煤柱失稳的机理中,得出突变失稳对应的控制变量变化路径及临界条件[14]。由于房式采空区中煤柱的稳定性是一个动态演化的过程且受众多因素的影响,需充分考虑煤岩单元塑性弱化、能量传递及损伤发展等非线性变化过程。元胞自动推理机可利用简单单元之间的相互作用规则,得到整个离散动力系统自组织演化的非线性数学模型[15],从而用于岩石类材料受载后动态演化过程的研究中[16-18]。上述研究成果从煤柱系统稳定性的角度分析并研究了煤柱的长期承载及失稳特征,而针对煤柱分形单元的损伤演化涉及较少,基于上述研究,采用元胞自动机的方法建立二维8Moore元胞房式煤柱稳定性评价模型,结合能量传递及元胞储能极限准则,动态演化煤柱元胞破坏失稳规律,通过有限差分模拟程序揭示房式煤柱单元失稳时序,确定煤柱内元胞动态失稳模式煤柱稳定特征,并结合现场试验评价模型的可靠性。
1 房式煤柱元胞自动机模型
1.1 元胞上覆均布载荷计算
选取品字形分布房式采空区煤柱群中1个煤柱作为研究对象,煤柱上方的受载情况如图1所示。
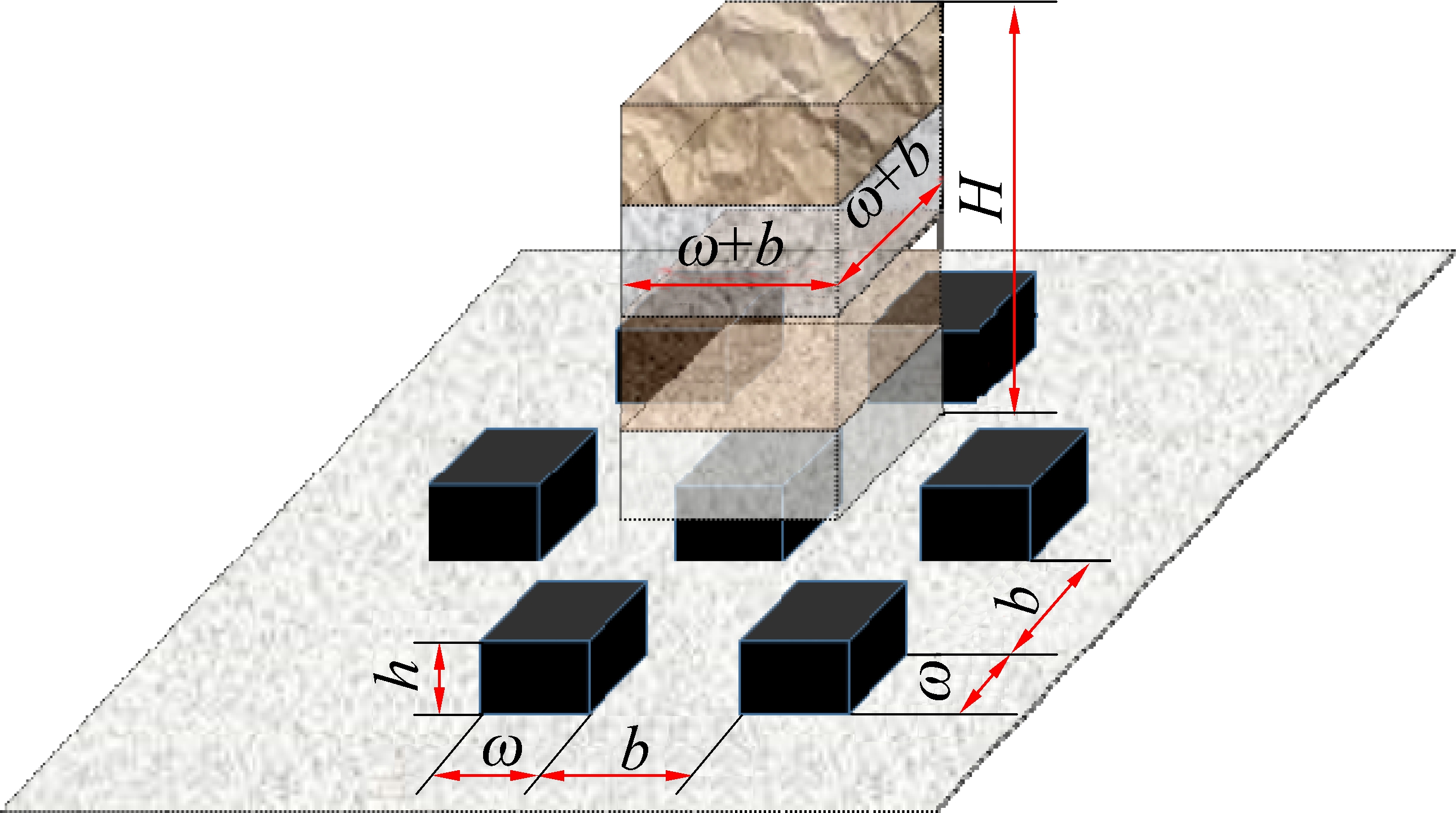
h—煤柱高度;H—开采深度;ω—煤柱截面边长;b—煤柱间距即煤房宽度
图1 房采煤柱受载示意
Fig.1 Schematic of loading coal pillars
结合图1,考虑房式采空区煤柱埋深较浅,采出宽度较小,采空区矸石不承载且每个煤柱承载特性相同等因素,采用有效面积理论对元胞上覆均布载荷进行估算,煤柱的水平截面形状及从属面积形状均为矩形,则煤柱元胞承受的均布载荷Lv可由式(1)表示[19]。
Lv=γH(ω+b)2/ω2
(1)
式中:γ为上覆岩层的平均容重。
1.2 元胞模型建立
采用8Moore元胞自动机模型将被研究的采空区煤柱沿其横截面离散成15×15的矩形网格,每个网格单元均为1×1的正方形,代表1个元胞,每个元胞的位置用(xi,yi)(i,j=1,2,…,15)表示。由于每个元胞单元的边长均为1,可用元胞吸收的广义能量代表系统施加的广义应力,且二者在量纲上保持统一。以E(xi,yi,t)代表各位置元胞单元t时刻存储的广义能量,等效于该元胞此刻存储的弹性应变能,则E(xi,yi,0)代表元胞初始广义能量。本模型将煤柱模型抽象为受损和完好2个部分,且规定已损部分不再具有承担载荷的能力,全部载荷将由未受损的部分承担。
1.3 元胞储能极限
假设煤柱为各向同性材料,除四角元胞外,位于模型内部的元胞均受到来自周围元胞群的约束作用,这种约束作用来自相连元胞之间的黏聚力以及四周元胞群上下表面所受摩擦力,定义元胞储能极限为使周围元胞群约束作用丧失时的元胞能量。在模型中,将这种约束作用等效于围压,不同围压对应不同的储能极限,元胞所受的围压状态及大小与元胞所处位置有关,由此定义二维元胞模型储能极限如图2所示。

图2 元胞储能极限分布
Fig.2 Cell storage limit distribution
由于模型采用15×15正方形元胞矩阵,所以整体元胞储能极限沿对角线对称分布,因此仅分析图2中黑色线框区域。图2中,一级元胞:位于模型四角的4个元胞,处于完全单轴压缩状态,所以储能极限最小,表示为U1;二级元胞:位于边缘一周除四角外的元胞,近似处于单轴压缩状态,但每个元胞两边存在较小约束,储能极限大于一级元胞,表示为U2;三级元胞:位于模型对角线上的元胞单元,处于等围压状态,研究表明,随着围压的增高,岩石的强度及储能极限大幅增长,总体呈幂指数形式[20]。本模型随着围压的逐渐增大,对应三级元胞的储能极限也随之呈幂指数增加,可由式(2)表示。
U3(xi,yi)=U1+σik
(2)
式中:σi为各位置三级元胞破坏所需的极限围压,(i=2,3,…,8);k为与煤岩物理力学性质相关的常数。
对于四级元胞:处于双向不等围压下其他位置的元胞,王云飞等[21]通过室内试验及颗粒流与Fish语言程序对煤岩进行不同围压组合试验,得出在最小主应力一定的情况下,随着中间主应力的增加,煤岩的弹性储能极限也随之线性增加,则在元胞模型中,在每一圈的四级元胞向中间移进的过程中,各四级元胞破坏所需的围压比n(中间主应力σ2/最小主应力σ3)随着增加,对应的储能极限也随之线性增加,可由式(3)表示。
U4(xi,yj)=U3(xi,yi)+kn
(3)
式中:U4(xi,yj)为各位置四级元胞储能极限(i≠j≠1);U3(xi,yi)为各位置三级元胞储能极限;n为四级元胞破坏的极限围压比。
三级元胞中位于模型中心的元胞处于最大等围压状态,且所受的约束力最大,储能极限值也最大。根据模型的对称性及储能极限分布规律得到模型中所有元胞的破坏极限阈值U(xi,yi),(i,j=1,2,3,…,15)。
1.4 元胞模型能量输入及传递规律
煤柱上方为均布载荷,因此系统广义能量的输入方式为恒定加载,每一时步对系统所有未破损元胞施加相同的广义能量,模拟煤柱上方的恒定均布载荷,随后元胞系统开始自动进行演化,在任意时步t内,计算该时步内每个元胞所存储的广义应变能E(xi,yi,t)若满足式(4)
E(xi,yi,t)≥U(xi,yi)
(4)
则认为该元胞破坏且不再具有承载能力,破坏元胞的一部分能量以等比例、等概率的形式传递给周围未破坏的邻居元胞,剩余的能量根据热力学第一定律以一定的能量耗散率损耗,系统满足能量守恒定律。
所有元胞按照上述规则进行演化,形成雪崩式的能量传递及元胞破损,直到某一时步t,输入广义能量后,系统内剩余各元胞的能量均小于其对应的储能极限阈值时,演化终止,结合破坏统计量D表示元胞模型的破坏程度
D=At/A
(5)
其中:At为演化终止时已破坏元胞的数量,即煤柱横截面上宏观破坏的表征;A为系统内元胞总数量(15×15)。当损伤量D达到一定值时,认为煤柱失稳。
2 演化结果分析
由于模型具有对称性,演化结果分析依旧以图2中黑色线框内的元胞为主。为便于描述演化过程及结果,假设所有元胞的初始能量均为0,并规定每个元胞破坏后向周围各元胞传递的能量为定值。由于模型破坏演化的形式主要取决于不同位置元胞所受约束力大小,若假定每个元胞在x、y轴方向上对其他元胞所提供的约束力均为σt,且随着轴向元胞数量增多,约束力线性叠加。对于对角线上的元胞,随着x的增加,对应元胞所受的最大约束(极限围压)也随之线性增加,如式(6)所示。
σi=xσt
(6)
式中:σi为位于(xi,yi)处的三级元胞的最大约束(极限围压)。
而对于同圈的四级元胞,其围压比也会随着x近似线性变化,如式(7)所示。
n=k1x
(7)
式中:k1为煤岩单元围压变化系数,随着y增加逐渐减小。
将式(6)及式(7)分别代入式(2)和式(3)中,可得式(8),即
(8)
将式(8)统一到同一坐标中,其中横坐标为煤柱二维元胞模型的x轴,纵坐标为各元胞储能极限值U,如图3所示。

图3 Ⅰ型演化元胞储能极限变化
Fig.3 First evolutionary of cell energy storage limit change
其中,一级元胞储能极限最低,在施加广义能量后最先破坏,随后二级元胞逐渐全部破坏,而三级与四级元胞的破坏有2种情况,对应以下2种演化模式。
Ⅰ型演化:由图3可知,每圈所有四级元胞储能极限均小于其紧邻内圈三级元胞的储能极限,在能量加载过程中,储能极限阈值较小的元胞容易先行破坏。如图4所示,由于对角三级元胞的储能极限均大于其紧邻外圈四级元胞的极限阈值,且假设的每个元胞破坏后向周围元胞传递能量的值相同,在演化过程中只有当外圈四级元胞先开始破坏或全部破坏时,紧邻内圈的三级元胞才开始破坏。而在同一圈中只有当三级元胞破坏后,四级元胞才开始破坏,因此煤柱的破坏过程呈逐层演化形式,其弹性核区逐渐向矩形转化,演化特性如图4b、图4c、图4d所示,并在图4b、图4c、图4d之间不断转化;随着演化逐渐转向内部,三级元胞的储能极限不断增加,直至某一步时演化停止,煤柱趋于稳定,最终的弹性核区如图4d所示呈矩形。

图4 Ⅰ型演化过程
Fig.4 First evolutionary model
演化初期元胞的损伤较剧烈,损伤当量D随着时步先急剧增加后逐渐平缓,代表煤柱逐渐趋于稳定。由于初期破坏主要为一级元胞与二级元胞,且二级元胞储能极限相同,边缘煤柱破坏较快,因此初期演化破坏较剧烈,损伤当量D也随之急剧增加。当边缘元胞全部破坏后,演化向内部转移,破坏主要以四级元胞为主,三级元胞破坏较少。
Ⅱ型演化如图5所示,每圈的四级元胞中均存在1个与其紧邻内圈三级元胞储能极限相等的元胞,称之为等效元胞,位于等效元胞前的四级元胞储能极限小于该三级元胞储能极限,之后的四级元胞极限值大于该三级元胞储能极限值。

图5 Ⅱ型演化元胞储能极限变化
Fig.5 Second evolutionary of cell energy storage limit change
Ⅱ型演化元胞的破坏特征同样服从极限值较小的元胞先破坏的规律,演化也是先由一级元胞开始破坏,随后二级元胞逐渐全部破坏,并诱发紧邻内圈的三级元胞及四级元胞逐层破坏。元胞破坏演化特征如图6a、图6b、图6c所示,与Ⅰ型演化初期(一级、二级及可能的三级和四级元胞破坏)的演化过程相一致,但由于Ⅱ型演化每圈四级元胞中等效元胞的存在,位于等效元胞之后的四级元胞储能极限值大于该元胞储能极限值,且四级元胞储能能力由外向里逐渐递增,因此Ⅱ型演化四级元胞整体储能极限要大于Ⅰ型演化。当2种演化中三级元胞储能极限及外部施加广义能量相同时,Ⅱ型演化四级元胞的损伤破坏范围较Ⅰ型演化小,则演化终止时Ⅱ型演化的弹性核区形态特征如图6d所示近似呈四周凸起的多边形。

图6 Ⅱ型演化过程
Fig.6 Second evolution mode
由此可见,Ⅱ型演化的演化过程中也是初期损伤较多,损伤当量先急剧增加,后逐渐趋于缓和。但由于Ⅱ型演化四级元胞破坏范围较小,最终稳定后弹性核区总面积要大于Ⅰ型演化,因此稳定性相比Ⅰ型演化更好。
3 数值模拟
为研究房式采空区下单个煤柱破坏演化的特性,结合石圪台煤矿3-1-1煤层房式开采现状,建立FLAC3D数值模拟模型,模型外界尺寸为10 m×10 m×38 m,煤柱尺寸为6 m×6 m×2 m,如图7所示。

图7 煤柱数值计算模型
Fig.7 Coal column numerical calculation model
结合现场现状及岩石力学试验得出岩层各分层的岩性,见表1[10]。
表1 煤岩力学参数
Table 1 Coal and rock mechanics parameters
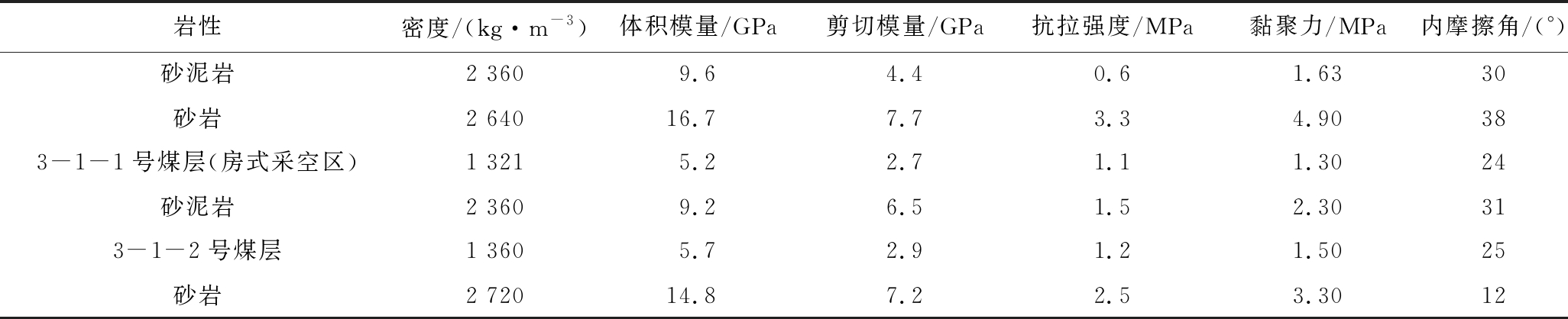
岩性密度/(kg·m-3)体积模量/GPa剪切模量/GPa抗拉强度/MPa黏聚力/MPa内摩擦角/(°)砂泥岩2 3609.64.40.61.6330砂岩2 64016.77.73.34.90383-1-1号煤层(房式采空区)1 3215.22.71.11.3024砂泥岩2 3609.26.51.52.30313-1-2号煤层1 3605.72.91.21.5025砂岩2 72014.87.22.53.3012
模型下表面固支,顶底板岩层四周表面施加法向位移约束,煤柱四周无约束,模型上表面施加1.0 MPa垂直应力,侧压系数为1.2。塑性区演化结果如图8所示。
由图8a可知,由于煤柱的边缘处于单向受力状态,所以煤柱4个角先出现剪切破坏,随后应力向煤柱内部转移,使边缘煤柱单元依次塑性破坏,并致使紧邻内圈煤柱的对角单元破坏,如图8b所示一级元胞及二级元胞全部破坏。由图8c可知,在图8b向图8c过渡期间,对角单元不再产生破坏,而其紧邻外圈单元从两端开始向里逐渐破坏,这与元胞模型Ⅱ型演化图6c对应;由图8d可知,模拟计算至平衡,煤柱的弹性核区形态呈四周凸起的多边形,与Ⅱ型演化最终弹性核区形态特征相对应。

图8 数值计算模拟结果
Fig.8 Numerical calculation simulation results
数值模拟结果表明:煤柱的破坏主要为剪切破坏,且同样由外向里渐进式破坏,其弹性核区分布变化规律与元胞模型的Ⅱ型演化一致,由此揭示房式采空区煤柱的稳定演化服从Ⅱ型演化,同时验证了煤柱元胞自动机模型的可靠性。
4 现场实例
乌兰集团石圪台煤矿3-1-1号煤层埋深较浅,为确保生态环境不遭到破坏,采用房式采煤法开采3-1-1号煤层,煤柱及煤房宽度均为6 m,经过多年后形成房式采空区,遗留大量煤柱,通过对现场1435房采工作面采空区进行表土层剥离揭露,揭露后处于稳定状态下的煤柱如图9所示。

图9 房式采空区表土层剥离试验
Fig.9 Topsoil stripping experiment reveals room coal pillar
由图9a可知,揭露后的房式煤柱呈“品”字形分布,煤柱均处于稳定状态,且煤柱尺寸基本相同。选取其中稳定性较好的煤柱(在图9a中红色线框标出)并放大如图9b所示,此时煤柱四周存在塑性区并有少量煤块脱落,表明一级元胞及二级元胞已全部破坏,煤柱水平截面弹性核区的形态特征与Ⅱ型演化结论及数值模拟结果一致,大致呈四周凸起的多边形(图9b中红色虚线所示)。表明提出的房式煤柱稳定性元胞演化模型及数值模拟结果的可靠性强,可为后续房式采空区煤柱稳定性分析提供新的研究思路。
5 结 论
1)基于房式采空区承载特性,采用元胞自动推理机理论,建立了二维煤柱元胞模型,结合围压对煤岩储能极限影响规律定义了元胞模型的储能极限分布规律,推演出房式煤柱的2种演化模式,其中Ⅰ型演化最终弹性核区近似呈矩形,Ⅱ型演化最终弹性核区近似呈四周凸起的多边形。
2)Ⅱ型演化模式每圈的四级元胞中存在与紧邻内圈三级元胞储能极限相同的等效元胞,其整体元胞储能极限高于Ⅰ型演化模式,在同样演化规则及外部施加相同广义能量的条件下,Ⅱ型演化模式的稳定性相对较好。
3)采用FLAC3D模拟了煤柱、煤房宽度均为6 m时的浅埋房式采空区煤柱,煤柱整体稳定性较好,煤柱塑性区及弹性核区的演化规律与Ⅱ型演化相一致。
4)通过对石圪台煤矿3-1-1号煤层房式采空区煤柱进行揭露试验得出,煤柱均处于稳定状态,且煤柱水平截面弹性核区形态特征与Ⅱ型演化相对应,由此验证了房式煤柱元胞演化模型及数值模拟结果的正确性。
[1] 张永爱. 房式采空区遗留煤炭资源回收及生态重建[J]. 煤矿安全,2014,45(2):197-199.
ZHANG Yongai.Residual coal resource recovery and ecological reconstruction for room mining goaf[J].Safety in Coal Mines,2014,45(2):197-199.
[2] 李正胜,李宏杰. 房柱式采空区影响下露天端帮煤开采安全控制技术[J].煤炭科学技术, 2020, 48(8):76-81.
LI Zhengsheng, LI Hongjie. Safety control technology of open-pit end wall coal mining under influence of room pillar gob[J].Coal Science and Technology,2020,48(8):76-81.
[3] 刘成勇. 房柱式采空区对下分层复采矿压显现的影响规律研究[J]. 煤炭科学技术, 2020,48(5):41-49.
LIU Chengyong. Study on influence law of room and pillar gob on pressure behavior of lower seam mining[J].Coal Science and Technology, 2020,48(5):41-49.
[4] 杜计平,孟宪锐. 采矿学[M]. 徐州:中国矿业大学出版社,2014,556.
[5] JIANG Bangyou,WANG Lianguo,LU Yinlong. Ground pressure and overlying strata structure for a repeated mining face of residual coal after room and pillar mining[J]. International Journal of Mining Science & Technology,2016,26(4):645-652.
[6] 李海清,向 龙,贾宏宇. 品字形房柱式采空区开采地表移动规律[J]. 地下空间与工程学报,2011,7(3):541-546.
LI Haiqing,XIANG Long,JIA Hongyu.The laws of surface movement in the pin-pillar style mining goaf area[J]. Chinese Journal of Underground Space and Engineering,2011,7(3):541-546.
[7] 解兴智. 浅埋煤层房柱式采空区顶板-煤柱稳定性研究[J]. 煤炭科学技术,2014,42(7):1-4,9.
XIE Xingzhi.Study on stability of roof-coal pillar in room and pillar mining goaf in shallow depth seam[J]. Coal Science and Technology,2014,42(7):1-4,9.
[8] 刘彩平,王金安,侯志鹰. 房柱式开采煤柱系统失效的模糊理论研究[J]. 矿业研究与开发,2008,28(12):8-9,12.
LIU Caiping,WANG Jin′an,HOU Zhiying. Study on failure of coal-pillar system in room-and-pillar mining based on fuzzy set theory[J].Mining Research and Eevelopment,2008,28(1):8-9,12.
[9] 彭小沾,崔希民,王家臣,等. 基于Voronoi图的不规则煤柱稳定性分析[J]. 煤炭学报,2008,33(9):966-970.
PENG Xiaozhan,CUI Ximin,WANG Jiachen,et al. Stability analysis of irregular coal pillars based on Voronoi diagram[J]. Jouranal of China Coal Society,2008,33(9):966-970.
[10] 朱德福,屠世浩,王方田. 浅埋房式采空区煤柱群稳定性评价[J]. 煤炭学报,2018,43(2):390-397.
ZHU Defu,TU Shihao,WANG Fangtian.Stability evaluation on pillar system of room and pillar mining in goaf at shallow depth seam[J]. Journal of China Coal Society,2018,43(2):390-397.
[11] M NAJAFI. Probabilistic analysis of stability of chain pillars in Tabas coal mine in Iran using Monte Carlo simulation[Z]. E JALALI S M,F SErRESHKI,2016:1,25-35.
[12] WATTIMENAR K. Predicting the stability of hard rock pillars using multinomial logistic regression[J]. International Journal of Rock Mechanics and Mining Sciences,2014,71:33-40.
[13] SCOTT. Evaluation of the stability of underground rock pillars through a probabilistic approach[J]. American Journal of Applied Sciences,2012,9(8):1273-1282.
[14] 王方田,屠世浩,李召鑫. 浅埋煤层房式开采遗留煤柱突变失稳机理研究[J]. 采矿与安全工程学报,2012,29(6):770-775.
WANG Fangtian,TU Shihao,LI Zhaoxin.Mutation instability mechanism of the room mining residual pillars in the shallow depth seam[J]. Journal of Mining & Safety Engineering,2012,29(6):770-775.
[15] VON NEUMANN J,BURKS A W. Theory of self-reproducing automata [M]. Urbana:University of Illinois Press,1996.
[16] 尹光志,张东明,王 浩. 岩石损伤断裂的沙堆元胞自动机模拟[J]. 岩土力学,2005,26(6):986-989.
YIN Guangzhi,ZHANG Dongming,WANG Hao.A BTW approach to damage and fracture of rock [J].Rock and Soil Mechanics,2005,26(6):986-989.
[17] 马志涛,谭云亮. 岩石破坏演化细观非均质物理元胞自动机模拟研究[J]. 岩石力学与工程学报,2005,24(15):2704-2708.
MA Zhitao,TAN Yunliang.Simulation study of rock failure based on MH-PCA model[J].Chinese Journal of Rock Mechanics and Engineering,2005,24(15):2704-2708.
[18] 谭云亮,颜 伟,马洪岭. 细观非均质岩石蠕变特征的物理元胞自动机模拟[J]. 岩土力学,2006,27(S1):9-12.
TAN Yunliang,YAN Wei,MA Hongling.Creep simulation for MESO-heterogeneous rock based on MH-PCA model[J].Rock and Soil Mechanics,2006,27(S1):9-12.
[19] 胡炳南. 条带开采中煤柱稳定性分析[J]. 煤炭学报,1995,20(2):205-210.
HU Bingnan.Stability analysis of coal pillars in strip mining[J]. Jouranal of China Coal Society,1995,20(2):205-210.
[20] 张志镇,高 峰. 受载岩石能量演化的围压效应研究[J]. 岩石力学与工程学报,2015,34(1):1-11.
ZHANG Zhizheng,GAO Feng.Confining pressure effect on rock energy[J]. Chinese Journal of Rock Mechanics and Engineering,2015,34(1):1-11.
[21] 王云飞,郑晓娟,赵洪波. 双向不等围压煤岩破坏能量演化机理与能量强度准则[J]. 安全与环境学报,2016,16(6):59-65.
WANG Yunfei,ZHENG Xiaojuan,ZHAO Hongbo.Energy evolution mechanism and energy intensity criteria for destructive energy of two-dimensional confining coal and rock[J].Journal of Safety and Environment,2016,16(6):59-65.
