0 引 言
从文献[1-2]中可以发现一个重要力学现象,即进行锚杆(索)拉拔试验时,当拉拔荷载加到一定数值,锚杆(索)体未从孔内拔出,岩体试件却伴随巨响或震动,瞬间沿钻孔径向发生整体开裂。该现象表明,在拉拔试验过程中,钻孔孔壁受到很大的径向压力,致使岩体试件开裂。由于这种径向压力足以引起整个试件迅速开裂,可见其对锚杆承载力的影响是不可忽视的,在实际锚固工程中,整个岩体是不可能被挤裂的,因此这种径向压力作用就愈加明显。分析认为,钻孔孔壁形态是产生这个径向应力的最主要因素。
与此类似,文献[3]对钻孔灌注桩桩侧阻力分析时,提出过孔壁粗糙度对桩侧阻力和抗拔力有较大影响,认为这种影响可达20%~40%,在其分析中采用孔壁凹凸度因子与岩石单轴抗压强度相乘。文献[4]分析了结构面粗糙角i对其抗剪强度的影响,认为当法向压力较小时,i提高了滑移面的内摩擦角,从而使其抗剪能力提高。文献[5]从起伏差对有约束滑移面的法向应力有较大影响的角度去考虑,但没有考虑实际工程中存在的初始法向应力[6]。PATTON[7]对岩-岩结构面剪切特性研究后认为结构面剪切过程必须考虑剪胀角的影响。同时,很多扩孔理论的研究成果表明,岩土类材料在受力过程中产生剪胀现象。同时,很多扩孔理论的研究成果表明,岩土类材料在受力过程中产生剪胀现象。如传统的Vesic扩孔理论分析了孔中的挤土效应[8-9]。蒋明镜[10-12]等通过多种测试形成了扩孔理论基础,也有学者运用Mohr-Coulomb强度理论推导了考虑剪胀的扩孔理论解析解[13-15]。范文等[16]基于统一强度理论并考虑剪胀效应,详细推导了柱形孔扩孔问题的统一解。综上所述,诸多国内外学者对孔壁或结构面形态的影响进行了大量研究,并取得了诸多有意义的成果,借鉴上述成果,引申考虑到目前锚杆设计和施工没有系统的孔壁形态对荷载传递以及承载力影响的理论支撑。
基于此,有必要对文献[1-2,5]中相关内容再深入分析,系统地研究孔壁形态对锚杆荷载传递以及承载力的影响。在考虑锚杆钻孔孔壁粗糙形态的前提下,基于非线性Mohr-Coulomb强度准则,结合荷载传递函数法和锚固体-围岩结构面剪胀效应及破坏机理,建立了适应于圆形巷道锚杆锚固体应力传递模型,分别推导出了破坏和弹性条件下锚固体轴力及剪应力解析式。基于所获得的解析式,深入探讨了锚固体轴力随剪胀角即钻孔孔壁粗糙度变化的分布规律和随圆形巷道应力场切向应力变化的分布规律。对钻孔孔壁形态对锚杆荷载传递的影响有了一个规律性的认识,建议在实际锚固工程设计和施工中适当考虑。
1 非线性Mohr-Coulomb强度准则
岩土工程中常采用线性Mohr-Coulomb非强度准则,在这个强度准则中,最大主应力σ1和最小主应力σ3呈线性关系,其表达式为
σ1=qp+Mpσ3
(1)
其中:qp、MP为试验常量,与岩土的抗剪强度指标c、φ关系为
Mp=(1+sin φ)/(1-sin φ),qp=2ccos φ/(1-sin φ),
然而,试验表明在软弱的围岩中,最大主应力σ1和最小主应力σ3的关系是非线性关系,而线性关系只是其中的特例,其非线性曲线见式(2)。
(2)
其中,![]() 和α是由三轴实验确定的参数。式(2)是BIENIAWSKI于1974年首次提出的,是在线性Mohr-Coulomb强度准则的基础上发展起来的。在应力空间(τ,σn)中,式(2)的等价表达式为
和α是由三轴实验确定的参数。式(2)是BIENIAWSKI于1974年首次提出的,是在线性Mohr-Coulomb强度准则的基础上发展起来的。在应力空间(τ,σn)中,式(2)的等价表达式为
τ=c0(1+σn/σt)1/m
(3)
其中:τ为切应力;c0为曲线与纵轴的截距;σn为正应力;c0、σt和m为由三轴试验确定的岩土材料参数。当m=1时,式(3)变成线性Mohr-Coulomb强度准则,将式(3)绘制成曲线如图1所示。
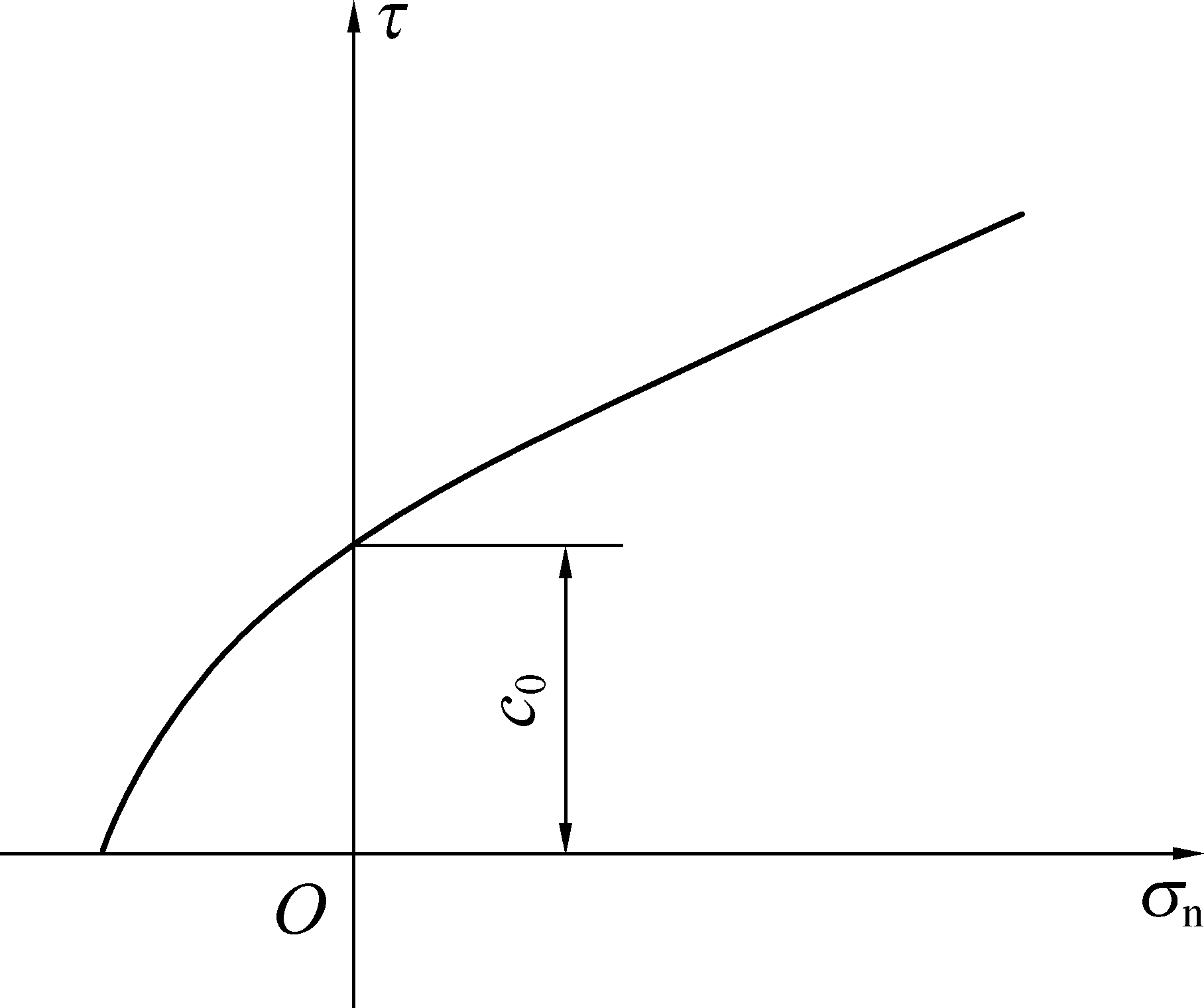
τ—切应力;σn—正应力;c0—曲线与纵轴的截距
图1 非线性屈服准则的切线
Fig.1 Tangent of nonlinear yield criterion
2 基于剪胀效应的应力计算模型
锚杆钻孔孔壁表面一般呈现沿轴线上下起伏的现象,这是由钻孔施工过程中钻杆上的钻头上下左右摆动造成的,尽量使钻孔孔壁凹凸[18]不平以提供足够的抗拉拔承载力。在进行锚杆拉拔试验过程中,锚固体-围岩界面法向应力增加,迫使围岩向外撑开,界面形成空隙,如图2所示。当围岩的弹性模量小于锚固体综合弹性模量时,围岩-锚固体界面的压力和剪应力是由于剪胀作用产生的,而不是锚固体受压时的侧向膨胀。

D—圆筒直径;ΔD—孔壁径向膨胀量;Δs—弹性位移变量;σn0—初始应力
图2 锚固体-围岩滑移示意
Fig.2 Diagram of anchor solids-wall rock slip
2.1 锚固体剪应力产生机理理论分析
由于锚杆钻孔孔壁存在凹凸不平的粗糙体,类似于岩石节理的起伏面,当锚固体-围岩界面滑移时,会出现滑移膨胀扩张现象,界面的法向应力增加,锚固体剪应力的产生主要由此引起。为便于理论推导,作如下假定:①锚固体为近似圆柱形;②锚固体-围岩结构面为不规则锯齿形起伏面,其起伏角为β;③沿锚固体轴线发生位移和破坏,破坏面为锚固体-围岩结构面。
根据厚壁圆筒弹性理论[19],当孔壁发生径向扩张ΔD时,产生的法向应力增量Δσn为
Δσn=[ErmΔD/(1+vr)D]
(4)
其中:Erm为围岩的弹性模量;ΔD为孔壁径向膨胀量;vr为围岩泊松比;D为圆筒直径。因为法向刚度k=Erm/[(1+vr)D]为常量,故法向应力增量与孔壁径向扩张成线性关系。
图2中不规则凸起为锚固体-围岩界面,当深度z处的锚固体-围岩的弹性位移为Δs(z),且凸起没有被剪断时,则孔壁的径向扩张为
ΔD=2tan β·Δs(z)
(5)
式中:β为剪胀角;Δs(z)为弹性位移。
将式(6)代入(5)得凸起没有被剪断时,则孔壁的法向应力增量表达式为
Δσn=2ktan βΔs(z) (Δs(z)<s0)
(6)
式中:s0为弹性极限位移。
由上述分析知,锚固体-围岩界面的实际法向应力由初始应力和剪胀应力增量2个部分构成,则剪应力本构模型如图3所示。第1阶段锚固体-围岩界面凸起没有剪断,剪应力与剪切位移成比例变化,处于弹性阶段;第2阶段锚固体-围岩界面凸起被剪断,锚固体-围岩界面剪切强度过渡为残余剪切强度,进入破坏阶段(锚固体作用机理如图4所示)。

图3 锚固体与围岩界面本构模型
Fig.3 interface constitutive model of anchor solids and surrounding rocks

图4 锚固体作用机理示意
Fig.4 Action mechanism of anchor solids
相应的表达式可表示为
(7)
其中:φu为锚固体-围岩界面内摩擦角;φr为锚固体-围岩界面凸起被剪断后的界面内摩擦角;s(z)为锚固体位移。由非线性Mohr-Coulomb强度准则知τ=c0(1+σn/σt)1/m,由当λ=1时,p=q,围岩处于静水应力状态圆形硐室应力场切向应力[6]为
σn=K0γh[1+R2/(z+R)2]
(8)
式中:K0为灌浆压力系数;γ上覆土层平均重度,kN/m3;h为巷道深度,m; R为圆形巷道半径,m;z为剪切位移。
2.2 荷载传递函数的理论推导
设锚固体截面积为A,周长为U,弹性模量为E,锚杆与锚固体共同变形;锚固体-围岩界面剪应力为τ(z)。假定锚固材料符合虎克定律,则在锚杆深z处取一锚固体微段,其长度为dz(图5),考虑应变与轴力的关系以及锚固体微段的静力平衡,由荷载传递函数法知
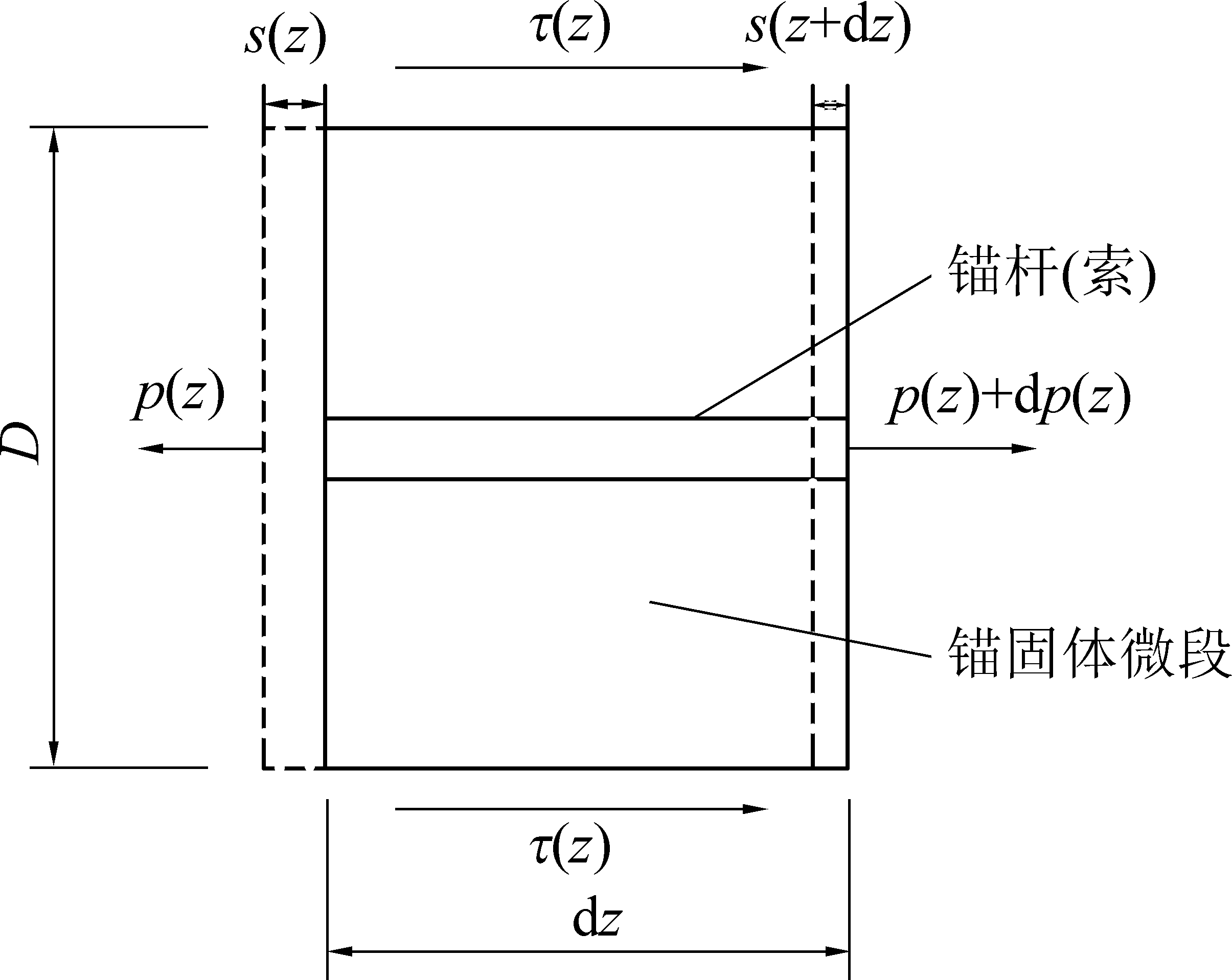
p(z)—锚固体轴力表达式即拉拔荷载;s(z)—锚固体位移表达式;s(z+dz)—锚固体微段的位移;p(z)+dp(z)—锚固体微段所受拉拔荷载
图5 锚固体微段的静力平衡示意
Fig.5 Schematic of static equilibrium of micro segment of anchor solid
(9)
2.2.1 破坏区理论分析
将式(7)中Δs(z)>s0时剪应力表达式代入式(9)得
(10)
假定作用于锚固体顶端的拉拔荷载为Pd时,锚固体相应的位移为sd,锚固体的长度为l。
则由边界条件:![]() 得:
得:
c1=-Pd/EA,c2=sd,并对τ进行幂级数展开得:
P(z)=Pd-(2Uktan βs0+M)z
(11)
式中,令M=c0[1+(1+K0γh)/σt]。
由式(11)知,当锚固体-围岩界面凸起被剪断时,锚固体-围岩界面过渡到残余强度τm,轴力在破坏区内呈线性分布规律。
2.2.2 弹性区理论分析
将式(7)中Δs(z)≤s0时剪应力表达式代入式(9)得
(12)
由边界条件:![]() 并对τ进行幂级数展开解得
并对τ进行幂级数展开解得
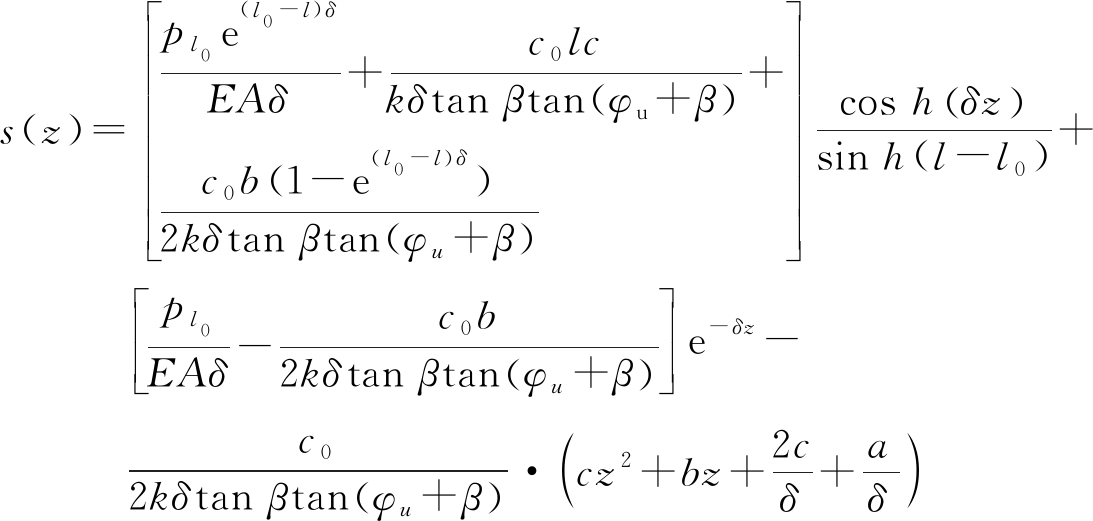
(13)
式中:l0为锚固体破坏区的长度;Pl0为锚固体l0处受到的拉拔荷载;δ为正常数;令
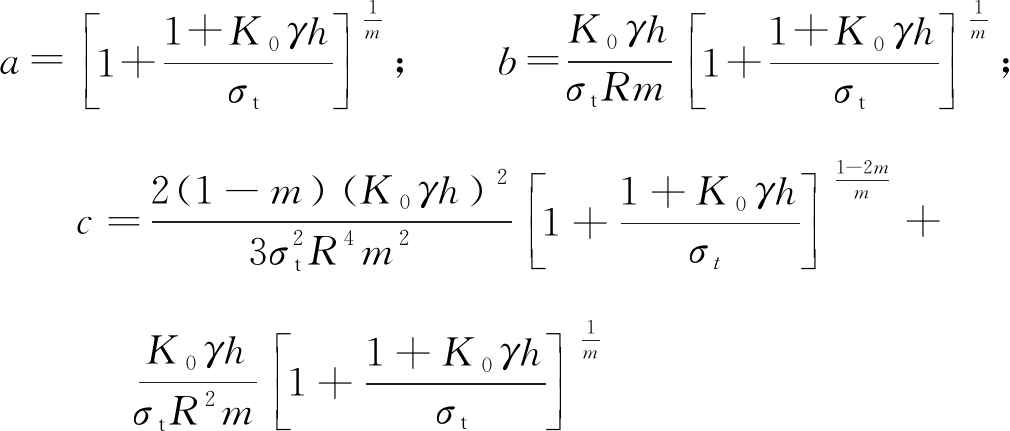
将式(13)代入式(9)解得锚固体的剪应力表达式为
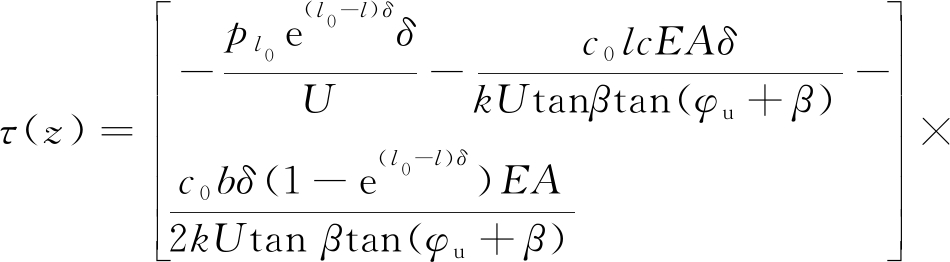
![]()
![]()
![]()
(14)
而锚固体的轴力表达式为
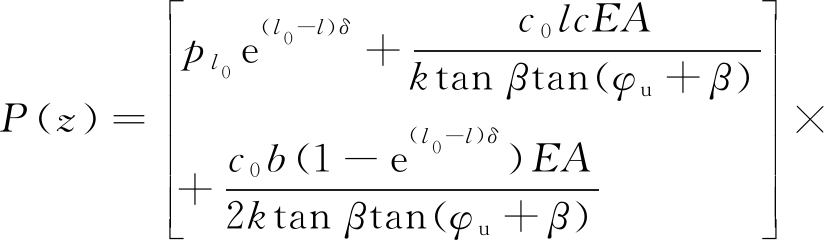
![]()
![]()
![]()
(15)
由以上推导分析知,在外加拉拔荷载的作用下,锚杆锚固体与围岩界面由于发生位移而产生剪胀效用,从而产生界面径向压力和剪应力。当锚固体-围岩界面凸起被剪断时,锚固体-围岩界面过渡到残余剪切强度τm,剪应力沿锚固体轴向分布重新分配,剪应力峰值点会向锚固段后部移动。剪应力的大小除与锚固体直径、上覆岩土层自重和围岩泊松比、弹性模量等物理力学性质有关外,主要受钻孔孔壁和锚固体界面的粗糙程度和灌浆压力等因素的影响,因此下面从锚固体—围岩界面粗糙程度和灌浆压力两方面分析对锚固体荷载传递性状的影响。
3 锚固体轴力和剪应力分布规律及影响因素
3.1 锚固体轴力和剪应力分布规律
由剪应力和轴力表达式(14)和(15)可知,锚固体应力分布和施加的拉拔荷载的大小有很大的关系,假定施加不同的拉拔荷载,取值分别为:50、80、100、150、200、300、350 kN,圆形巷道半径R=3 m,巷道埋深h=100 m,岩层容重γ=16 kN/m3,侧压系数λ=1,围岩弹性模量Erm=3×109 MPa,围岩泊松比υ=0.3,锚杆直径d=32 mm,孔径D=100 mm,砂浆弹性模量Es=2.0×104MPa,锚杆弹性模量Eg=2.0×105MPa,锚杆长度l=3 m,界面内摩擦角φu=35°,锚固体—围岩界面凸起被剪断后的界面内摩擦角φr=13°,剪胀角β=5°,m=3,c0=0.2 MPa,σt=0.3 MPa,则锚固体轴力和剪应力分布曲线分别如图6、图7所示。
由图6、图7分析可知,随着施加的拉拔荷载的增加,锚固段轴力和剪应力也随之增大,其作用范围也随之增大。因此,增大施加的预紧荷载可以有效地提高其锚固效果。但由此产生的最大剪应力必须小于界面之间的容许强度,以免出现界面破坏产生滑移,导致锚固效果降低或失效。

图6 不同拉拔荷载下锚固段轴力分布
Fig.6 Distribution of axial force in anchorage section under different drawing loads
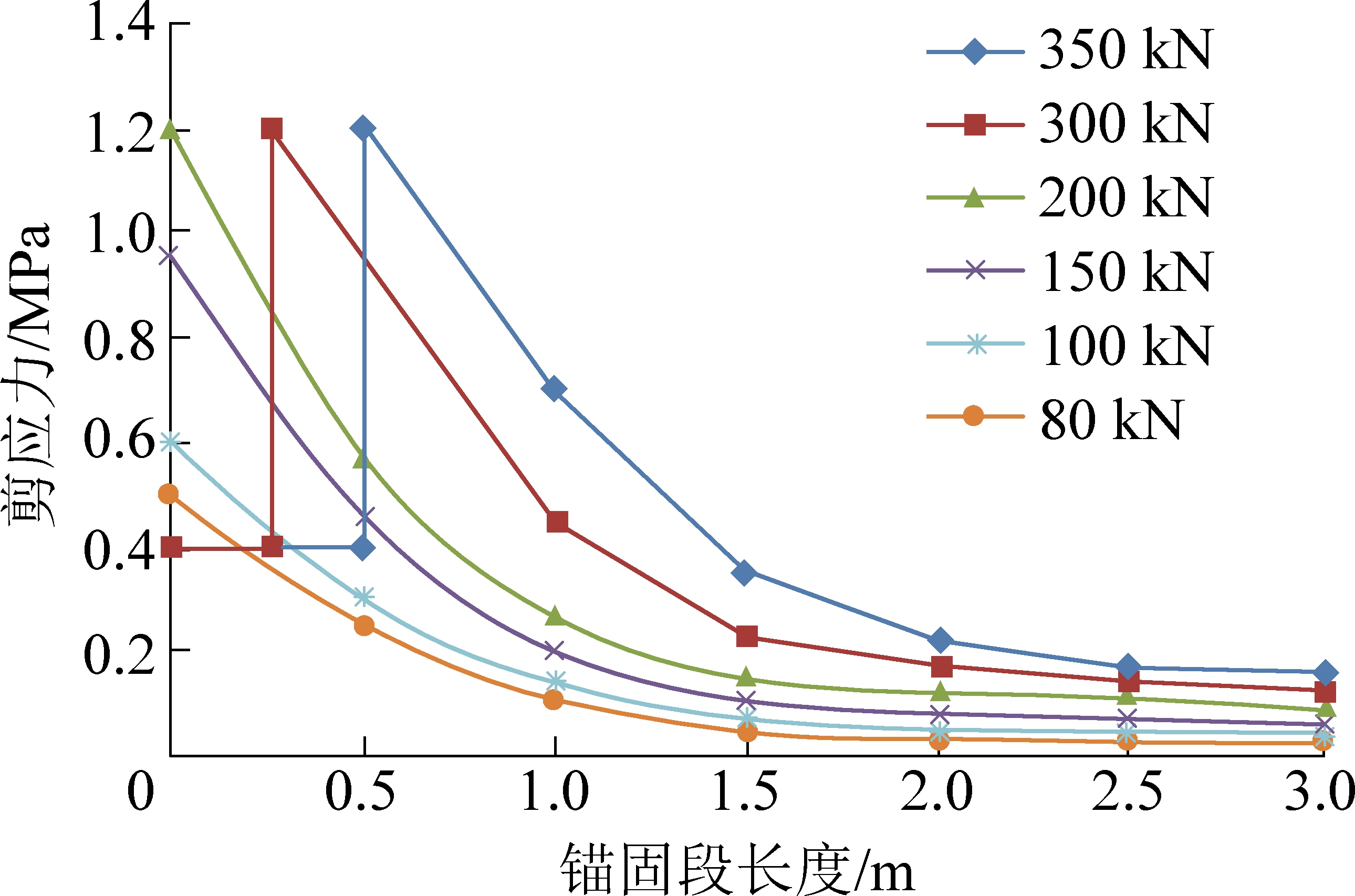
图7 不同拉拔荷载下锚固段剪应力分布
Fig.7 Shear stress distribution curve of anchorage section under different drawing loads
3.2 孔壁粗糙度对锚固体轴力分布的影响
由假设知孔壁粗糙度由剪胀角β体现,所以研究钻孔孔壁粗糙度对锚固体轴力分布的影响,就是β对锚固体轴力分布的影响。假定β分别为0°、3°、5°、8°,拉拔荷载为150 kN,其他参数同上,分析其对锚固体轴力分布的影响,根据式(15),其锚固体轴力分布曲线如图8所示。

图8 不同β时锚固体轴力分布
Fig.8 Axial force distribution of anchor solids with different β values
由图8知,随着β的增大,锚固体的轴力曲线斜率随之增大;剪胀角越大,轴力在锚固体顶端的分布就越集中,递减速率越大,荷载传递的深度越小。同等条件下,剪胀角越大即孔壁粗糙度越大,锚杆的抗拉拔性能越好,极限拉拔力越大。因此,在实际锚固工程中,建议适当增加孔壁的粗糙度以提高锚固效果。
3.3 初始应力对锚固体轴力分布的影响
在巷道深度和巷道半径一定时,根据式(9),初始应力大小主要取决于灌浆压力系数K0,假定灌浆压力系数K0分别为0.4、0.6、0.8、1.0、1.2,拉拔荷载为150 kN,其他参数同上,分析其对锚固体轴力分布的影响,根据式(15),其锚固体轴力分布曲线如图9所示。
由图9可知,随着灌浆压力系数K0的增大,锚固体的轴力曲线斜率随之增大;轴力分布曲线递减速率是随着初始应力的增大而增大,荷载在锚固体顶端的分布也越集中,荷载传递深度也随之减小。因此在不破坏岩土体整体性的前提下可以适当增加灌浆压力以提高锚杆的承载力。

图9 不同K0时锚固体轴力分布
Fig.9 Axial force distribution anchor solids with different K0 values
4 结 论
1)在考虑锚杆钻孔孔壁粗糙形态的前提下,基于非线性Mohr-Coulomb强度准则,结合荷载传递函数法和锚固体—围岩结构面剪胀效应及破坏机制,建立了适应于圆形巷道锚杆锚固体应力传递模型,分别推导得出破坏和弹性条件下锚固体轴力及剪应力解析式。
2)分析了孔壁粗糙度的变化对锚固体荷载分布的影响。同等条件下,剪胀角越大即钻孔孔壁粗糙度越大,锚杆的抗拉拔性能越好,极限拉拔力越大。因此,在实际的工程中,建议适当增加孔壁的粗糙度以提高锚固效果。
3)由圆形巷道应力场切向应力变化对锚固体轴力分布的影响进行了分析,在巷道深度和巷道半径一定时,初始正应力大小主要取决于灌浆压力系数K0,随着灌浆压力系数K0的增大,锚固体的轴力曲线斜率随之增大;轴力分布曲线递减速率是随着初始应力的增大而增大,荷载在锚固体顶端的分布也越集中,荷载传递深度也随之减小。说明注浆锚杆的围岩初始应力对锚杆的抗拉拔力有着重要的制约作用,因此在不破坏岩土体整体性的前提下可以适当增加灌浆压力来改善锚杆的承载性能。
[1] 徐景茂,顾雷雨.锚索内锚固段注浆体与孔壁之间峰值抗剪强度试验研究[J].岩石力学与工程学报,2004,23(22):3765-3769.
XU Jingmao,GU Leiyu. Testing study on the peak shear strength between grout and bore wall in the interior bond section of prestessed anchorage cable[J].Chinese Journal of Rock Mechanics and Engineering,2004,23(22):3765-3769.
[2] 杨永刚,杨张杰,余大军.小孔径预应力锚索内锚力增强技术研究[J].煤炭科学技术,2017,45(4):14-19.
YANG Yonggang,YANG Zhangjie,YU Dajun.Study on internal anchoring force enhanced technology of small diameter hole pre-stressed anchoring cable[J].Coal Science and Technology,2017,45(4):14-19.
[3] 张建新,刘利民.孔壁粗糙度对钻孔灌注桩桩侧阻力的影响[J].工程勘察,2003(1):13-15.
ZHANG Jianxin,LIU Limin. The effect of hole side roughness on the pile side resistance for cast-in-site pile[J].Geotechnical Investigation and Surveying,2003(1):13-15.
[4] 顾金才,沈 俊,陈安敏,等.预应力锚索加固机理与设计计算方法研究[C]//第八次全国岩石力学与工程学术大会论文集,成都:中国岩石力学与工程学会,2004:43-50.
[5] 顾雷雨,徐景茂,顾 欣,等.锚杆孔壁形态对其承载力影响分析[J].岩石力学与工程学报,2005,24(20):3771-3776.
GU Leiyu,XU Jingmao,GU Xi.Effect of geometric wave shape of anchor cable borehole wall on its bearing capacity[J]. Chinese Journal of Rock Mechanics and Engineering,2005,24(20):3771-3776.
[6] 谷拴成,苏 锋,崔希鹏. 煤巷复合顶板破坏规律分析[J]. 煤炭科学技术,2012,40(5):20-23.
GU Shuancheng,SU Feng,CUI Xipeng.Anslysis on deformation and failure law of complex roof in seam gareway[J].Coal Science and Technology,2012,40(5):20-23.
[7] PATTON F D.Multiple modes of shear failure in rock[C].Proceeding 1st Congress International Rock Mechanics Lisbon,1966:509-518.
[8] WILSON A H.A method of estimating the closure and strength of lining required indrivages surrounded by a yield zone[J] .Int J Rock Mech Min Sci,1980,17(6):349-355.
[9] VESIC A S. Expansion of cavities in infinite soil mass[J].ASCE-JSMFD,1972,98(3):265-290.
[10] 蒋明镜,沈珠江.考虑材料应变软化的柱形孔扩张问题[J].岩上工程学报,1995,17(4):10-19.
JIANG Mingjing,SHEN Zhujiang.The expansion of cylindrical holes for strain softening of materials is considered[J].Chinese Journal of Geotechnical Engineering,1995,17(4):10-19.
[11] 蒋明镜,沈珠江.岩土类软化材料的柱形孔扩张统一解问题[J].岩上力学,1996,17(1):1-8.
JIANG Mingjing,SHEN Zhujiang.A unified solution to the problem of cylindrical hole expansion for geotechnical softening materials[J].Rock and Soil Mechanics,1996,17(1):1-8.
[12] 蒋明镜,沈珠江.考虑剪胀的弹脆塑性软化柱形孔扩张问题[J].河海大学学报,1996,24(4):65-72.
JIANG Mingjing,SHEN Zhujiang.The expansion of elasto-embrittlement plastic softened cylindrical hole is considered[J].Journal of the Hohai University,1996,24(4):65-72.
[13] 王晓鸿,王家来,梁发云.应变软化岩上材料内扩孔问题解析解[J].工程力学,1999,16(5):71-76.
WANG Xiaohong,WANG Jialai,LIANG Fayun.An analytical solution to the problem of expanding holes in strain-softened rock[J].Engineering Mechanics,1999,16(5):71-76.
[14] 蒋明镜,沈珠江.考虑剪胀的线形软化模型柱形孔扩张问题[J].岩石力学与工程学报,1998,16(6):550-557.
JIANG Mingjing,SHEN Zhujiang.The cylindrical hole expansion problem of linear dilatant model is considered[J].Chinese Journal of Rock Mechanics and Engineering,1998,16(6):550-557.
[15] 邹金峰,彭建国,张进华,等.基于非线性Mohr-Coulomb强度准则下的扩孔问题解析[J].土木工程学报,2009,42(7):90-97.
ZOU Jinfeng,PENG Jianguo,ZHANG Jianhua.Analytical solution of cavity expansion with the non-linear mohr-coulomb failure rule[J].China CIvil Engineering Journal,2009,42(7):90-97.
[16] 范 文,廖红建,陈立伟.考虑材料剪胀及软化的扩孔问题的统一解[J].西安交通大学学报,2003,37(9):957-961.
FAN Wen,LIAO Hongjian,CHEN Liwei.Unified solution on expansion cavity considering material dilatancy and softening[J].Journal of Xi’an Jiaotong University,2003,37(9):957-961.
[17] 邹金峰,李 亮,杨小礼,等.基于非线性Mohr-Coulomb强度准则下锚索极限抗拔力研究[J].岩土工程学报,2007,29(1):107-111.
ZOU Jinfeng,LI Liang,YANG Xiaoyu,et al. Study on the ultimate pullout force of pre-stressed cable based on nonlinear Mohr-Coulomb failure criterion [J]. Chinese Journal of Geotechnical Engineering,2007,29(1):107-111.
[18] JGJ 120—2012建筑基坑支护技术规程[S].
[19] 李通林,谭学术. 矿山岩石力学[M].重庆:重庆大学出版1991.
