0 引 言
大地电磁测深法(Magnetotelluric,MT)是一种以天然电磁场作为场源的电磁勘探方法,被广泛地应用于固体矿产勘查、石油天然气勘探等领域[1]。大地电磁勘探资料反演技术难度大,其处理结果准确与否直接影响到地质解释的精度,是MT勘探的关键技术。大地电磁反演的最终目的是实现目标泛函的最优化。反演的方法分为线性反演[2-3 ]和非线性反演[4-6],两类算法的区别在于是否对目标函数进行线性化处理。两类算法各自有自己的缺陷,线性反演算法对初始模型比较依赖,容易陷入局部极小;非线性反演算法对初始模型依赖大幅减弱,但是随着模型参数的增加导致搜索空间呈几何级数增加。
大地电磁反问题是不适定问题,正则化处理[7]是获得反问题稳定解的有效方法。地球物理工作者将正则化的思想与大地电磁反演问题相结合,对数据目标泛函添加不同的稳定泛函,如最小模型稳定泛函、最光滑模型稳定泛函、最小支撑泛函、最小梯度支撑泛函等。
在经典的Tikhonov正则化框架下,可以选择零阶、一阶、二阶差分算子来获得最小、平缓、光滑解。如基于最平缓模型约束如Occam反演[8-11]、基于最光滑模型约束的NLCG反演[12],2种反演方法能得稳定平滑的反演结果;然而考虑到对地电界面进行清晰的成像,聚焦反演在MT资料处理中也有较多应用,能够获得较清晰的电性分界面[13-16]。光滑反演与聚焦反演均为正则化的处理方式,两者的区别在于正则化项。
大地电磁一维反演正则化反演中,比较典型的有Occam反演[8]和ARIA一维反演[17]。针对大地电磁反演问题的不适定性,特别对于二维和三维的反演,算法的收敛速度占重要地位[18-22]。2种正则化反演算法被提出,最小二乘光滑约束反演和同伦正则反演算法。其中同伦正则算法是将同伦延拓思想与Tikhonov正则化思想相结合,使算法具备了同伦算法对非线性问题的收敛性好的优点。在详细叙述2种算法的工作原理之后,采用理论模型和实测数据对2种算法的正确性和可靠性进行验证。
1 反演理论和方法
1.1 大地电磁反演理论
反演问题可表示为
d=F(m)
(1)
式中:d为N维观测数据向量;m为M维模型参数向量;F为正演响应算子。
反演问题是已知观测数据向量d,寻求合理的地下模型参数向量m来拟合观测数据向量d。式(1)是不适定问题,解具有不唯一性和不稳定性,因此需要正则化处理获得反演问题的稳定解。根据Tikhonov理论[7],构造反问题的目标泛函如下:
Φ(m)=φ(m)+αs(m)
(2)
式中:Φ(m)为目标泛函;φ(m)为数据目标泛函;s(m)为稳定泛函,其作用是使反演过程稳定;α为正则因子。
1.2 最小二乘光滑约束反演算法
最小二乘光滑约束反演采用基于先验模型的最光滑模型约束,在L2范数的框架下,反演的目标泛函表示为
![]()
![]()
(3)
式中:Wd和Wm分别为数据和模型加权矩阵;mapr是先验模型。
对目标泛函式(3)中的F(m)在m-mk处线性化代处理,则式(3)可表示为
Φ(m)≈||Wd(F(mk)+Jk(m-mk)-d)||2+
α||Wm(m-mapr)||2
(4)
式中:Jk为灵敏度矩阵;k为当前迭代次数。
令式(4)的一阶变分等于零,得到如下的迭代式,即
且有![]()
1.2 同伦正则反演算法
同伦算法最早用于方程求根,KALLER等[23]首次采用同伦算法求解反问题,提出了一种地震波射线快速追踪算法。其后,许多学者对同伦算法进行了研究[24-25]。同伦算法由于具有收敛性好的优点,因而是求解非线性问题的强有力工具。
同伦算法来源于代数拓扑学同伦算法是代数拓扑学中的一个基本概念,设均为拓扑空间,f和g是X到Y的连续映射,若存在连续映射H:X×[0,1]→Y,使得对任意的x∈X,有H(x,0)=f(x),H(x,1)=g(x),则称f和g同伦,并称H是连接f(x)和g(x)的一个同伦。
针对反问题(1),考虑用不动点同伦进行求解。将同伦技巧和Tikhonov正则化算法结合,构造了大地电磁反演目标泛,该泛函如下:
(5)
式中:m0是初始模型;α正则因子取0<α≤1。
将F(m)在mk处进行一阶泰勒展开,并令(5)式的一阶变分等于零,得到如下的迭代格式,即
mk+1=mk+Δα
(6)
(7)
当α=0时,式(5)为模型目标泛函g1(m)=||Wm(m-m0)||2,有唯一解m=m0;当α=1时,g2(m)=||Wd(d-F(m))||2为数据目标泛函。g1(m)的零点已知,g2(m)的零点是待求的参数。因此,反问题的解可以表示为从给定的问题到目标问题的一个连续逼近的过程。应用该方法求解反问题式(1),算法可以全局收敛到反问题的最优解,且在一定程度上改善了线性反演对初值的依赖性。
1.3 正则因子的选取
正则因子是数据目标泛函和模型目标泛函的折衷。正则因子较大,则反演结果过度强调模型约束;正则因子太小,表示反演结果过度注重拟合数据,从而压制了模型约束,这将导致反演结果容易受到噪声影响产生虚假异常。因此,合适的正则因子选择至关重要。在正则因子选取上,已有的工作有正则因子递降法[26],即是从初始的正则因子α0出发,每次迭代根据一定的步长递减正则因子。陈小斌2005年提出的MD和CMD方案[17],其以每一次迭代的数据目标泛函和模型目标泛函的商作为下一次的迭代正则因子的值。及Zhdanov提出的自适应算法[27]。
鉴于Morozov偏差原理在正则因子选取上有着广泛的研究和应用,按照Morozov偏差原理选取正则因子,即所求正则因子α的选取与原始数据的观测误差δ匹配,即满足以下
||F(m)-d||2=δ2
(8)
其中,δ是观测数据的误差水平,构造泛函如
ψ(α)=||F(m)-d||2-δ2=0
(9)
对(9)式进行一阶泰勒展开,则
ψ(α)≈l(α)=ψ(αk)+ψ′(αk)(α-αk)
(10)
令l(α)=0,则第k次迭代的Newton迭代格式为
(11)
2 算例分析
2.1 算例一
假设有3层K型地电模型具体的参数:视电阻率ρ1=10 Ω·m,ρ2=200 Ω·m,ρ3=20 Ω·m;深度h1=500 m,h2=2 000 m。反演过程中将Bostick反演结果作为反演的初始模型,最小二乘光滑约束反演结果如图1所示。
图1中的图标中的1表示最小二乘光滑约束反演算法正则因子由递降法决定[26];2表示正则因子由Morozov偏差原理选取。由图1a可得,采用偏差原理选取正则因子的最小二乘光滑约束反演结果与实际地电模型最吻合。和Bostick相比能更准确反映中间高阻体大小和位置。除此之外,还能看出同一种算法,正则因子的选取方法不同,反演效果也不同。本文偏差原理决定正则因子反演结果(图1a的红色曲线)比用递降法决定正则因子反演结果(图1a中蓝绿色曲线)效果好,更吻合真实模型。
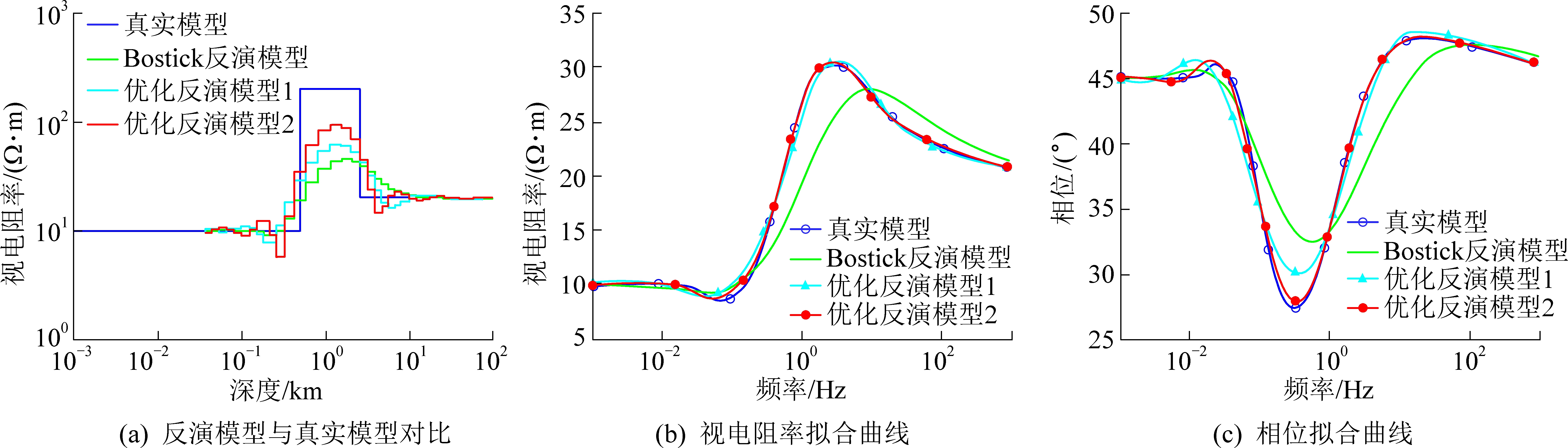
图1 K型地电模型反演结果对比
Fig.1 Comparison of inversion results of K-type geoelectric model
从图1b和图1c中可以看出,在数据的拟合程度上,采用偏差原理决定正则因子的最小二乘光滑约束反演比Bostick、采用递降法决定正则因子的最小二乘光滑约束反演的拟合效果要好。考虑到实测数据通常带有一定的误差,为了能够模拟真实的观测数据,验证算法的稳定性,对理论数据添加5%的随机高斯噪声进行反演,反演的结果如图2所示。由图2可知,加入5%的随机高斯噪声后反演的结果基本能反应出高阻体的位置和大小,说明了最小二乘光滑约束反演算法能有着良好的鲁棒性。图3给出了无噪声和 添加5%高斯随机噪声对应的迭代收敛曲线图。最小二乘光滑约束反演算法用偏差原理、递降法选取正则因子的收敛曲线分别对应图3中的红色、青绿色曲线。可知,用偏差原理决定正则因子对应的收敛曲线收敛速度更快,迭代次数少,说明了本文算法一定程度上提高了反演效率。

图2 K型地电模型的反演结果对比(添加5%噪声)
Fig.2 Comparison of inversion results of K-type geoelectric model(adding 5% noise)
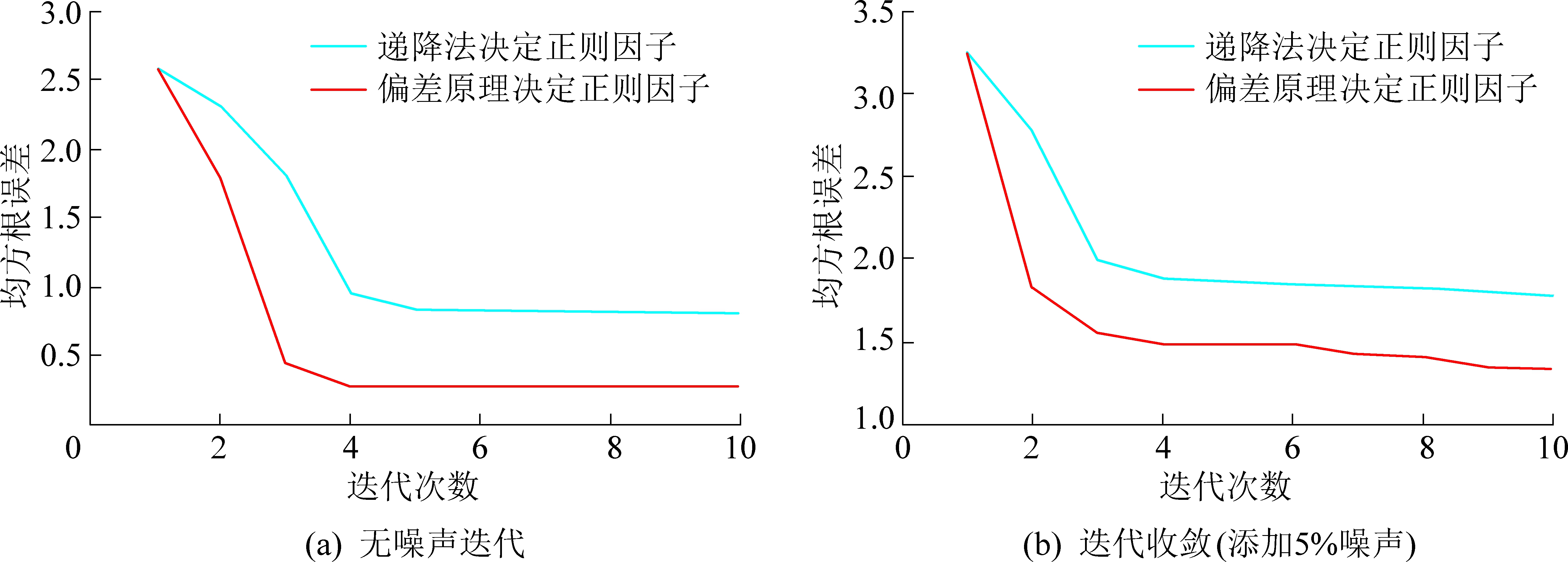
图3 迭代收敛曲线
Fig.3 Iterative convergence curves
2.2 算例二
假设有4层KH型地电模型具体的参数:视电阻率ρ1=30、,ρ2=200、ρ3=10、ρ4=100 Ω·m;深度h1=500 m,h2=1 000 m,h3=1 500 m。为了说明观测数据误差对反演的影响,对原始模型正演的数据分别添加了1%、5%、10%、20%的高斯随机噪声,并分别对不同的噪声水平进行同伦正则反演。算法反演的结果见表1。
表1 四层地电模型的反演结果
Table 1 Inversion results of four-layer geoelectric model

模型ρ1/(Ω·m)ρ2/(Ω·m)ρ3/(Ω·m)ρ4/(Ω·m)h1/mh2/mh3/m真实参数30.00200.0010.00100.00500.001 000.001 500.00无噪声29.99199.9910.0099.99499.991 000.001 500.001%噪声30.01196.5510.2399.46491.88992.221 526.785%噪声29.21142.0310.47103.97446.311 058.531 599.3210%噪声30.12153.7511.1398.37453.53978.891 389.2420%噪声30.08136.736.7875.70438.511 258.62796.50
由表1可知,同伦正则反演能很好的反演地电模型参数,且有着很好的抗噪能力。图4—图6分别给出了反演结果和模型正演结果在无噪声、5%噪声和20%噪声条件下的视电阻率和相位拟合效果图。

图4 KH型地电模型的反演拟合结果(无噪声)
Fig.4 Inversion fitting result of KH type geoelectric model(no noise)
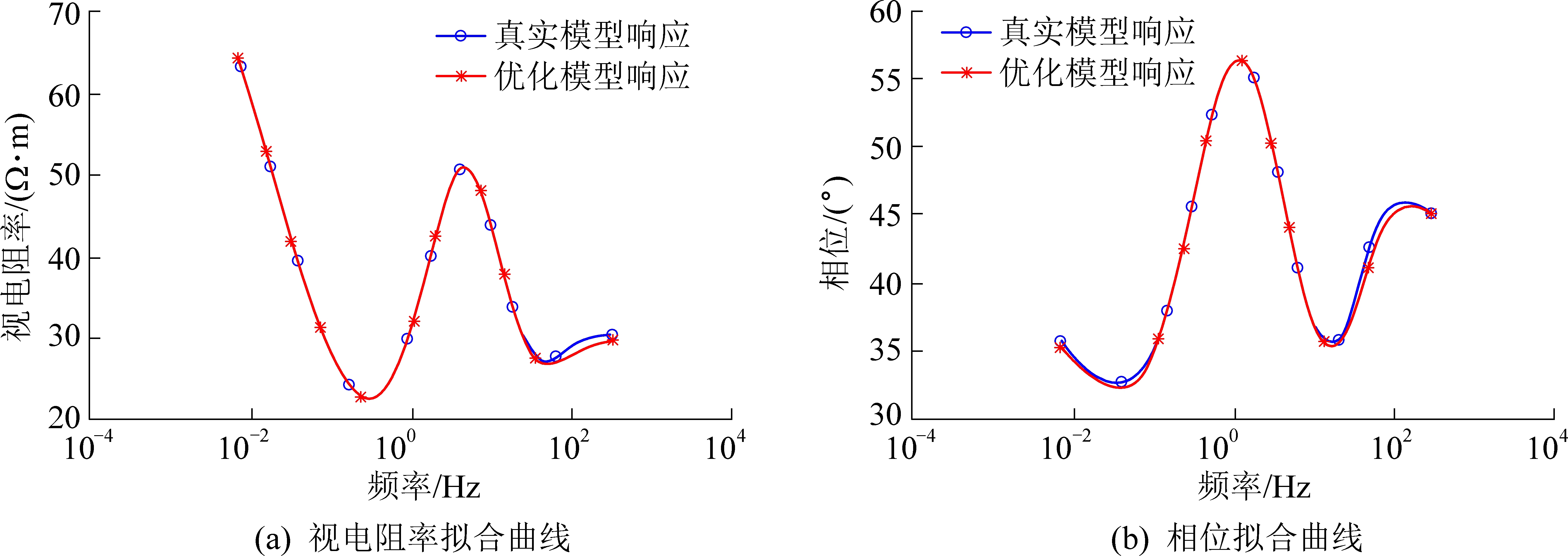
图5 KH型地电模型的反演拟合结果(5%噪声)
Fig.5 Inversion fitting result of KH type geoelectric model(5% noise)
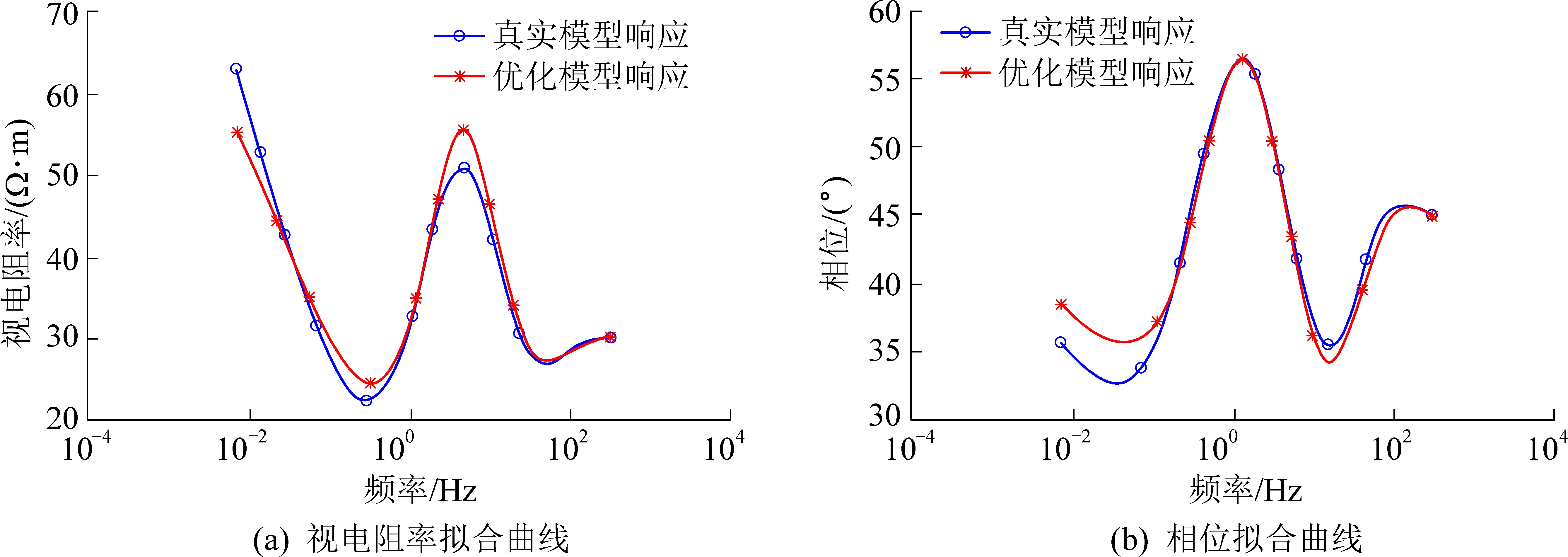
图6 KH型地电模型的反演拟合结果(20%噪声)
Fig.6 Inversion fitting result of KH type geoelectric model(20% noise)
2.3 实测数据反演
为进一步验证同伦正则反演算法的有效性,对实测数据进行反演。实测数据来自文献[28],是吉林桦皮厂地热田的一个实测点数据,用一个七层的地电模型对该实测数据进行反演,将反演结果和Bostick反演、及比较常用的线性算法Occam的反演的结果进行了对比。图7给出了3种算法的视电阻率和相位的拟合曲线。针对视电阻率曲线的拟合结果来看,虽然Occam反演与同伦正则反演较结果整体优于Bostick算法。但是Occam的高频部分拟合较差,而同伦正则反演算法在高低频的拟合效果都较好;从相位曲线的拟合结果来看,Bostick在高低频的拟合效果较好,中频的拟合效果较差,Occam在高低频段拟合效果较差,而同伦正则算法效果是最佳的。说明了本文算法用于实测大地电磁的反演也十分有效。

图7 实测数据反演结果对比
Fig.7 Comparison of inversion results of measured data
3 结 论
1)给出了2种正则化算法:最小二乘光滑约束反演与同伦正则反演算法。其中,首次将同伦正则反演应用到大地电磁反演中。2种算法应用到不同地电模型中,均取得较好的反演结果。体现了算法的有效性和稳健性。
2)正则因子的选取上,两种算法均采用偏差原理决定正则因子。算例一将其与传统正则因子递减法的反演结果进行了对比分析,证明了用偏差原理选取正则因子,效率更高,反演效果更好。
3)同伦正则反演算法是考虑到同伦算法收敛性好的优点,构造了目标泛函,并成功应用在大地电磁一维反演中。将来,可以尝试将此算法推广到大地电磁二维、三维的反演中。
[1] 汤井田,任政勇,周 聪,等.浅部频率域电磁勘探方法综述[J].地球物理学报,2015,58(8):2681-2705.
TANG Jingtian,REN Zhengyong,ZHOU Cong,et al. Frequency-domain electromagnetic methods for exploration of the shallow subsurface:a review[J]. Chinese Journal of Geophysics,2015,58(8):2681-2705.
[2] WANG K,CAO H,DUAN C,et al. Three-dimensional scalar controlled-source audio-frequency magnetotelluric inversion using tipper data[J]. Journal of Applied Geophysics,2019,164:75-86.
[3] XIANG Yang,YU Peng,ZHANG Luolei,et al. Regularized magnetotelluric inversion based on a minimum support gradient stabilizing functional[J]. Earth,Planets and Space,2017,69(1):158.
[4] GODIO A,SANTILANO A. On the optimization of electromagnetic geophysical data:Application of the PSO algorithm[J].Journal of Applied Geophysics,2018,148:163- 174.
[5] LI Siyu ,WANG Shuming ,WANG Pengfei,et al. An improved grey wolf optimizer algorithm for the inversion of geoelectrical data[J]. Acta Geophysica,2018,66(4):607-621.
[6] JAMASB A,MOTAVALLI-ANBARAN S H,GHASEMI K. A novel hybrid algorithm of particle swarm optimization and evolution strategies for geophysical non-linear inverse problems[J]. Pure and Applied Geophysics,2019,176(4):1601-1613.
[7] TIKHONOV A N,ARSENIN V Y,Solutions of ill-posed problems[M].New York:John Wiley and Sons,1977.
[8] CONSTABLE S C,PARKER R L,CONSTABLE C G. Occam’s inversion:a practical algorithm for generating smooth models from electromagnetic sounding data[J]. Geophysics,1987,52(3),289-300.
[9] DEGROOTHEDLIN C,CONSTABLE S. Occam’s inversion to generate smooth,two-dimensional models from magnetotelluric data[J]. Geophysics,1990,55(12),1613-1624.
[10] LI Yaoguo,OLDENBURG D W. 3-D inversion of magnetic data[J]. Geophysics,1996,61(2),394-408.
[11] Siripunvaraporn W,Egbert G. An efficient data-subspace inversion method for 2-D magnetotelluric data[J]. Geophysics,2000,65(3),791-803.
[12] RODI W,MACKIE R L. Nonlinear conjugate gradients algorithm for 2-D magnetotelluric inversion[J]. Geophysics,2001,66(1),174-187.
[13] ZHDANOV M,TOLSTAYA E. Minimum support nonlinear parametrization in the solution of a 3D magnetotelluric inverse problem[J]. Inverse Problems,2004,20(3),937-952.
[14] 张罗磊,于 鹏,王家林,等. 二维大地电磁尖锐边界反演研究[J]. 地球物理学报,2010,53(3):631-637.
ZHANG Luolei,YU Peng,WANG Jialin,et al. A study on 2D magnetotelluric sharp boundary inversion[J]. Chinese Journal of Geophysics 2010,53(3),631-637.
[15] ZHANG Luolei,KOYAMA T,UTADA H,et al. A regularized three-dimensional magnetotelluric inversion with a minimum gradient support constraint[J]. Geophysical Journal International,2012,189(1),296-316.
[16] PORTNIAGUINE O,ZHDANOV M S. Focusing geophysical inversion images[J]. Geophysics,1999,64(3),874-887.
[17] 陈小斌,赵国泽,汤 吉,等. 大地电磁自适应正则化反演算法[J]. 地球物理学报,2005,48(4),937-946.
CHEN Xiaobin,ZHAO Guoze,TANG Ji,et al. An adaptive regularized inversion algorithm for magnetotelluriv data[J].Chinese Journal of geophysics,2005,48(4),937-946.
[18] MACKIE R L,MADDEN T R,WANNAMAKER P E. Three-dimensional magnetotelluric modeling using difference equations:theory and comparisons to integral equation solutions[J]. Geophysics,1993,58(2),215-226.
[19] NEWMAN G A,ALUMBAUGH D L. Three-dimensional magnetotelluric inversion using non-linear conjugate gradients[J].Geophysical Journal International,2000,140(2),410-424.
[20] KELBERT A,MEQBEL N,EGBERT G D,et al. Modem:a modular system for inversion of electromagnetic geophysical data[J]. Computers & Geosciences,2014,66,40-53.
[21] DE Groot-Hedlin C,CoNSTABLE S. Inversion of magnetotelluric data for 2D structure with sharp resistivity contrasts[J]. Geophysics,2004,69(1),78-86.
[22] MACKIE R L,MADDEN T R. 3-dimensional magnetotelluric inversion using conjugate gradients [J]. Geophysical Journal International,1993,115(1),215-229.
[23] KELLER H,PEROZZI D. Fast seismic ray tracing[J]. SIAM Journal on Applied Mathematics,1983,43(4):981-992.
[24] EVERETT M. Homotopy,polynomial equations,gross boundary data,and small Helmholtz systems[J].Journal of computational physics,1996,124(2):431-441.
[25] BAO Gang,LIU Jun. Numerical solution of inverse scattering problems with multi-experimental limited aperture data[J]. SIAM Journal on Scientific Computing,2003,25(3):1102-1117.
[26] 吴小平,徐果明. 大地电磁数据的Occam反演改进[J]. 地球物理学报,1998,41(4),547-554.
WU Xiaoping,XU Guoming. Improvement of occam’s inversion for MT data[J]. Chinese Journal of Geophysics,1998,41(4):547-554.
[27] ZHDANOV M S,Geophysical inverse theory and regularization problems[M].Elsevier ,2002.
[28] 陈小斌.大地电磁正反演新算法研究及资料处理与解释的可视化集成系统开发[D].北京:中国地震局地质研究所,2003.
