0 引 言
水力压裂作为一种非常规油气藏的增产技术,已经广泛应用在页岩气开采中[1]。页岩储层为低渗透储层,通过水力压裂产生大量裂缝,以改造页岩储层渗透性实现增产[2]。地质调查与现场研究发现页岩储层中存在较多的天然裂缝,会影响水力压裂裂缝的扩展路径,继而对裂缝内压裂液和支撑剂的流动产生影响[3-5]。因此考虑天然裂缝影响下的页岩水力压裂数值模拟工作对页岩气的增产开发具有重要意义[6]。
许多学者通过试验手段研究了压裂裂缝的扩展规律[7-8]。文献[9-10]通过室内试验和理论分析总结了水力裂缝与天然裂缝相互作用准则,提出了水力裂缝贯穿天然裂缝的条件。认为水力裂缝与天然裂缝相交作用表现为:水力裂缝的穿越、天然裂缝的张开与水力裂缝的阻止3种行为。朱宝存等[11]利用有限元方法分析了地应力、天然裂缝对煤岩水力压裂起裂压力的影响。KHOEI等[12]基于扩展有限元方法利用力学响应模拟了水力裂缝与天然裂缝交点的关系。DAHI 等[13]提出了一种基于丰富节点的数值模型,研究了不渗透介质中水力裂缝被天然裂缝阻止情况下的裂缝交叉点关系。KESHAVARZI等[14]假设水力裂缝中保持恒定、均匀的净压力,研究了水力裂缝与天然裂缝之间的相互作用。KHOEI等[15]利用一个交叉富集函数来表示裂缝之间的交点,模拟了流体驱动裂缝与摩擦性天然断层之间的相互作用,利用罚函数法表示断层表面之间的摩擦接触行为,但假设裂缝内的流体压力是恒定的。文献[16-17]利用扩展有限元方法采用伦肖-波拉德判据,确定水力裂缝与天然裂缝交点的穿越或阻止行为。研究了摩擦型天然裂缝与胶结型天然裂缝的差异,发现含摩擦型天然裂缝的页岩储层的水力压裂裂缝网络更加复杂。
以上研究为水力裂缝与天然裂缝相交作用提供了理论基础,但在计算过程为简化计算往往忽略裂缝内的流体流动,只是施加均匀水压,这与实际情况不符。同时对于水力裂缝与天然裂缝相交后的裂缝扩展变化规律研究较少,天然裂缝对水力压裂得到压裂裂缝影响规律不明晰。因此笔者在考虑岩石储层基质变形、裂缝内的流体流动以及天然裂缝与水力裂缝的相交作用情况下,建立了二维水力压裂裂缝相交扩展模型。对水平应力差、天然裂缝相交角与天然裂缝长度影响裂缝相交前后的水力压裂裂缝扩展问题进行了研究。
1 水力压裂裂缝相交扩展模型
假设页岩储层Ω为不可渗透的线弹性均质体,水力压裂裂缝相交扩展模型中分别含有水力裂缝和天然裂缝。Q0为压裂液注入点速度;Γf和Γu分别为模型的外力与位移边界;Γc为裂缝水压边界;![]() 为外力;p为裂缝内流体压力;u为位移;s为裂缝长度;l为水力裂缝总长,模型如图1所示。
为外力;p为裂缝内流体压力;u为位移;s为裂缝长度;l为水力裂缝总长,模型如图1所示。
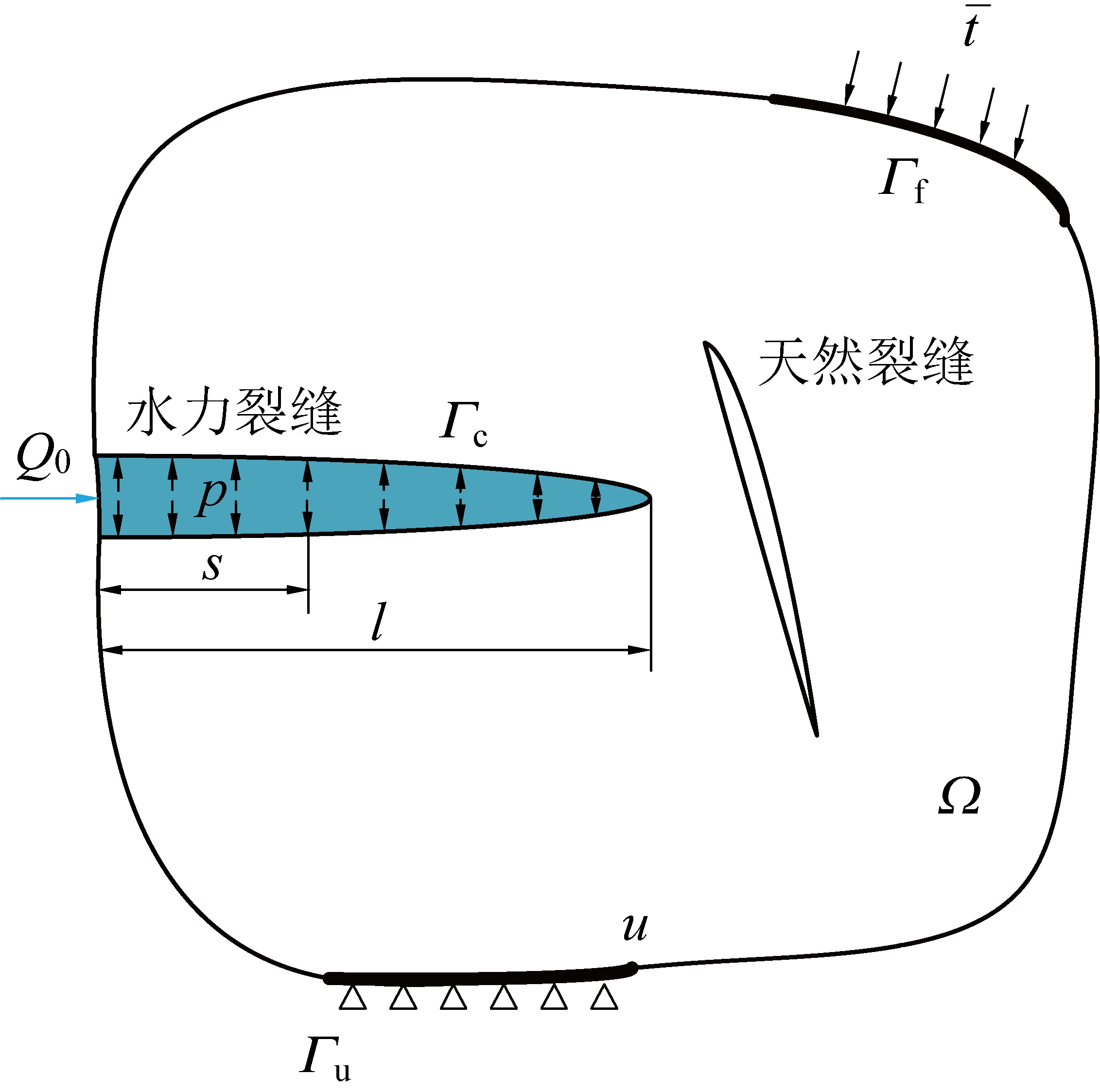
图1 水力压裂裂缝相交扩展模型示意
Fig.1 Schematic of intersection propagation model of hydraulic fracturing
1.1 岩石基质变形方程
水力压裂模型中的岩石基质在地应力和水力裂缝内的流体压力共同作用下发生变形,基于线弹性理论方程得岩石基质变形控制方程为
∇·σ+tb=0
(1)
式中:∇为Laplace算子;σ为应力张量;tb为体力张量。
对应的边界条件如式(2)所示,即
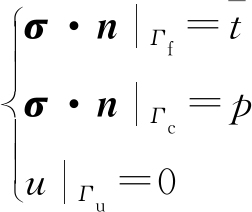
(2)
1.2 水力裂缝内渗流方程
假设水力裂缝内流体是不可压缩牛顿流体,水力裂缝内流体流动方程由润滑理论定律可得[18]
(3)
式中:q为流体流量;w为水力裂缝张开宽度;μ为流体黏度。
设t为时间,则水力裂缝内流体应满足局部质量守恒定律,则有
(4)
将式(3)代入式(4)可得
(5)
同时满足整体质量守恒方程式(6),即
(6)
压裂液注入点为定流量条件,注入速率为Q0。假设裂尖宽度为0,流体无滞留,则边界条件为
(7)
1.3 裂缝相交与扩展准则
当水力裂缝与天然裂缝发生相交作用时,水力裂缝尖端与天然裂缝相交如图2所示。其中β为水力裂缝与天然裂缝相交角,σH和σh分别表示最大水平地应力和最小水平地应力,τβ和σβ,n为作用于天然裂缝表面剪切力和法向力。
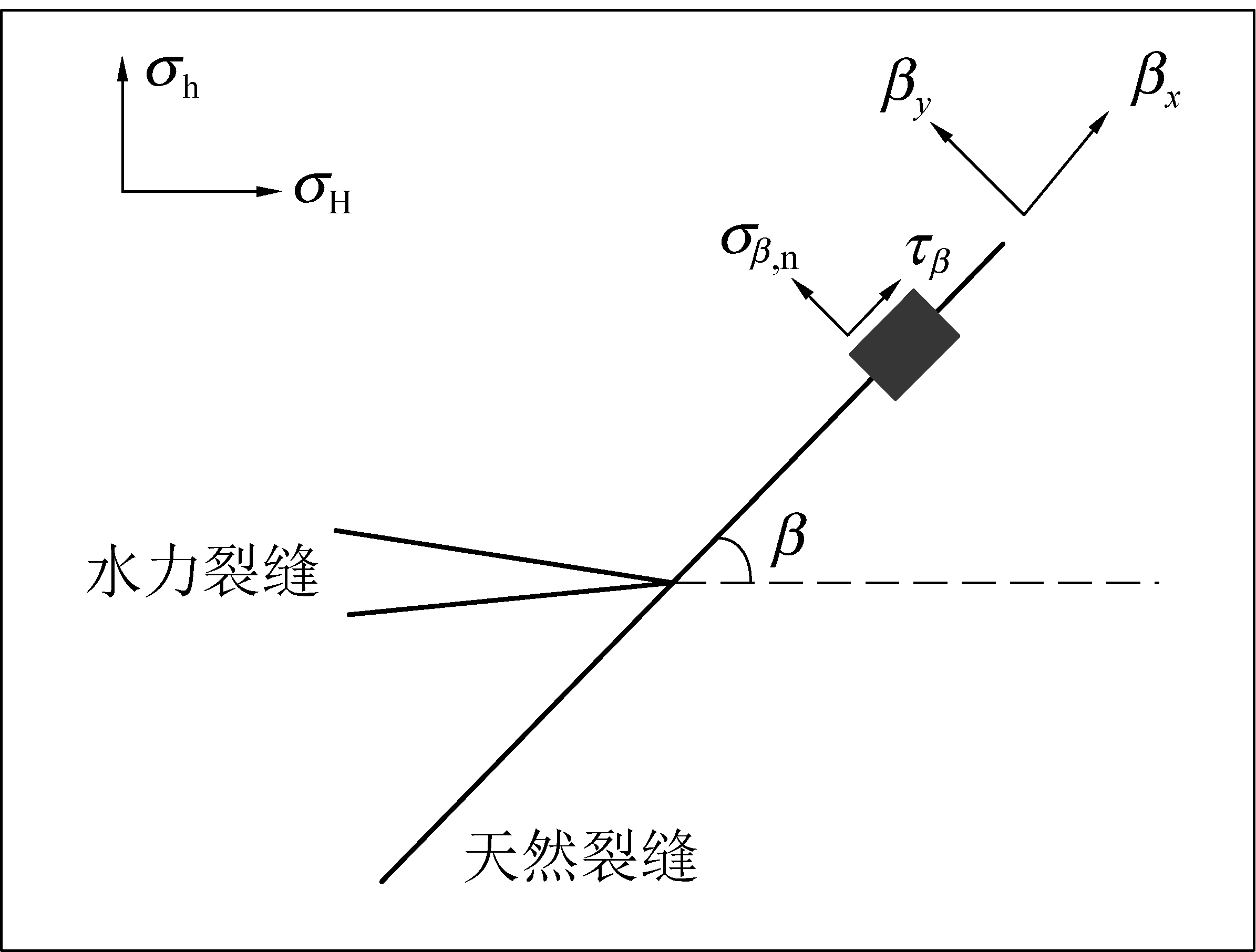
图2 水力裂缝与天然裂缝相交应力场示意
Fig.2 Schematic of stress field at intersection of hydraulic fracture and natural fracture
当最大主应力σ1大于岩石抗拉强度T0,且天然裂缝摩擦面不发生滑移,水力裂缝将穿越天然裂缝,在天然裂缝另一侧岩石基质中产生一个新裂缝,其临界条件 [10]为
σ1=T0
(8)
|τβ|<C-μfσβ,n=0
(9)
式中:τβ和σβ,n为作用于天然裂缝表面剪切应力和法向应力;C为天然裂缝界面黏结力;μf为天然裂缝摩擦因数。
裂缝扩展行为采用最大周向应力准则进行判断[19]。先利用相互积分法计算的裂缝尖端应力强度因子KⅠ与KⅡ,通过比较破裂方向等效应力强度因子Ke与岩体的断裂韧度KIC,即可获得对应的裂缝是否扩展。其临界条件为
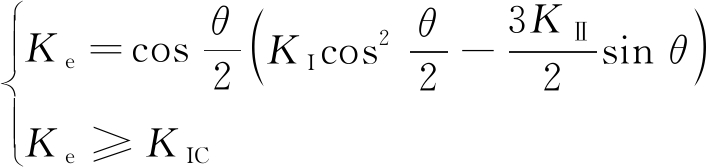
(11)
裂缝起裂角θ计算公式为
(12)
水力压裂裂缝相交扩展模型的求解是考虑岩石基质变形与裂缝内流体流动的非线性流固耦合问题。笔者以岩石基质变形位移和裂缝内流体压力作为基本变量,采用扩展有限元方法和有限元方法分别对岩石基质变形方程和裂缝内渗流方程进行离散,利用Newton-Raphson方法全耦合求解模型,编制了数值程序,进行数值模拟研究。
2 模型验证
为验证水力压裂裂缝相交扩展模型的正确性,分别与经典KGD模型解析解和Blanton室内水力压裂试验结果进行了对比。
2.1 与KGD模型对比
首先对无天然裂缝存在时的二维水力压裂裂缝扩展数值结果与经典KGD模型解析解[20]比较,数值计算输入参数如下:
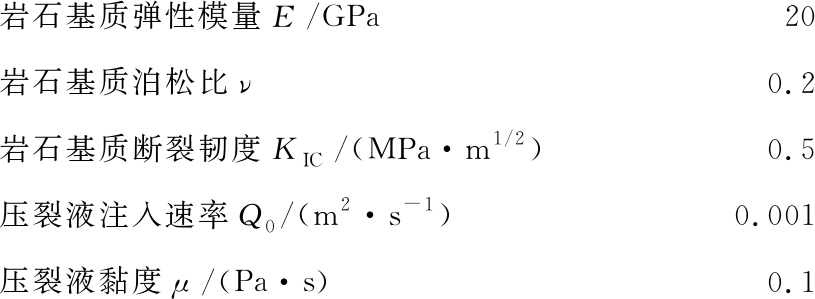
岩石基质弹性模量E/GPa20岩石基质泊松比ν0.2岩石基质断裂韧度KIC/(MPa·m1/2)0.5压裂液注入速率Q0/(m2·s-1)0.001压裂液黏度μ/(Pa·s)0.1
注水压力随时间变化关系如图3所示,可知数值计算结果与经典KGD模型解析解基本吻合,两者误差为1.1%,初步验证了模型的正确性。
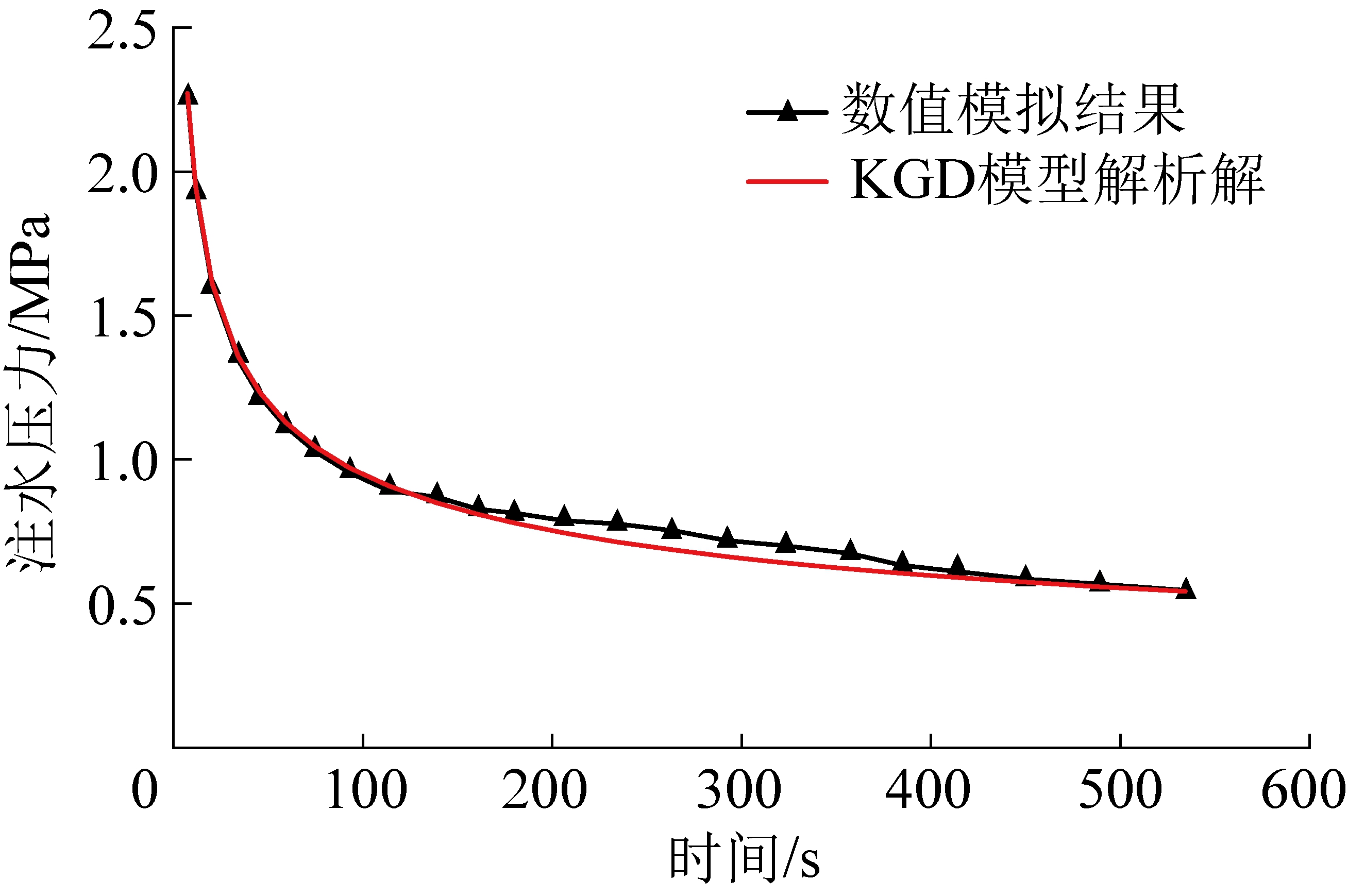
图3 注水压力变化曲线
Fig.3 Curves of water injection pressure
2.2 与Blanton试验对比
BLANTON等[9]在室内进行了三轴应力状态下预压裂材料水力压裂试验,研究了水力裂缝与天然裂缝在不同水平应力差和裂缝相交角下扩展情况。为验证本模型考虑水力裂缝与天然裂缝相交作用时的正确性,进行了6种水平应力差和4种相交角度组合下的水力压裂数值试验对比Blanton室内试验,其中水平应力差Δσ=σH-σh。计算模型如图4所示,区域模型具体参数如下:

岩石基质弹性模量E/GPa15岩石基质泊松比ν0.25岩石基质断裂韧度KIC/(MPa·m1/2)0.176岩石基质抗拉强度T0/MPa3.1天然裂缝摩擦因数μf0.75天然裂缝黏结力C/MPa0压裂液注入速率Q0/(m2·s-1)0.001压裂液黏度μ/(Pa·s)0.1

图4 水力裂缝与天然裂缝相交计算模型
Fig.4 Calculation model for intersection of hydraulic fracture and natural fracture
相交角等于60°时,应力差分别为2 MPa和15 MPa情况下的水力裂缝与天然裂缝相交扩展情况(图5)。可知在应力差为2 MPa时,水力裂缝与天然裂缝相交后,天然裂缝张开,水力裂缝沿天然裂缝轨迹扩展。此时天然裂缝段的宽度沿相交点上下出现差异性变化,天然裂缝上段受水力裂缝产生的诱导应力影响,其宽度小于天然裂缝下段宽度。当应力差为15 MPa时,水力裂缝直接穿越天然裂缝继续传播。11组数值试验结果与Blanton试验的对比结果见表1,除了一种结果外,其余都与Blanton试验结果相同,由此验证了笔者建立的水力压裂裂缝相交扩展模型的有效性。
表1 数值模型与Blanton试验对比结果
Table 1 Comparison between numerical model and Blanton’s experiment
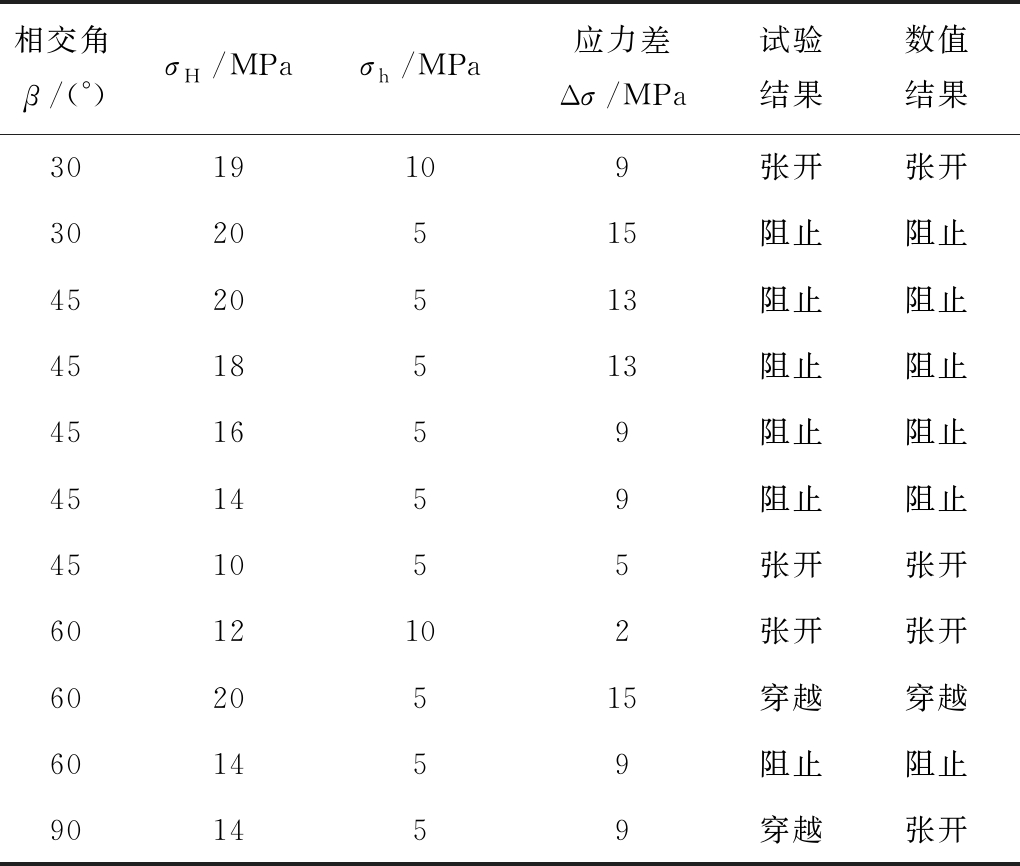
相交角β/(°)σH/MPaσh/MPa应力差Δσ/MPa试验结果数值结果3019109张开张开3020515阻止阻止4520513阻止阻止4518513阻止阻止451659阻止阻止451459阻止阻止451055张开张开6012102张开张开6020515穿越穿越601459阻止阻止901459穿越张开

图5 不同水平应力差下水力裂缝与天然裂缝相交结果
Fig.5 Simulation results of hydraulic fracture interacting with natural fracture at different horizontal stress differences
3 裂缝相交扩展数值模拟
3.1 水平应力差对裂缝扩展的影响
为研究水平应力差Δσ对水力裂缝与天然裂缝相交后裂缝扩展的影响,进行了当水平应力差Δσ分别为0、1、2、3 MPa时的水力压裂数值试验。计算模型,为25 m×25 m的正方形区域。模型四周受最小水平主应力σh和最大水平主应力σH作用,沿模型中央点建立xoy坐标系(图6)。初始水力裂缝半
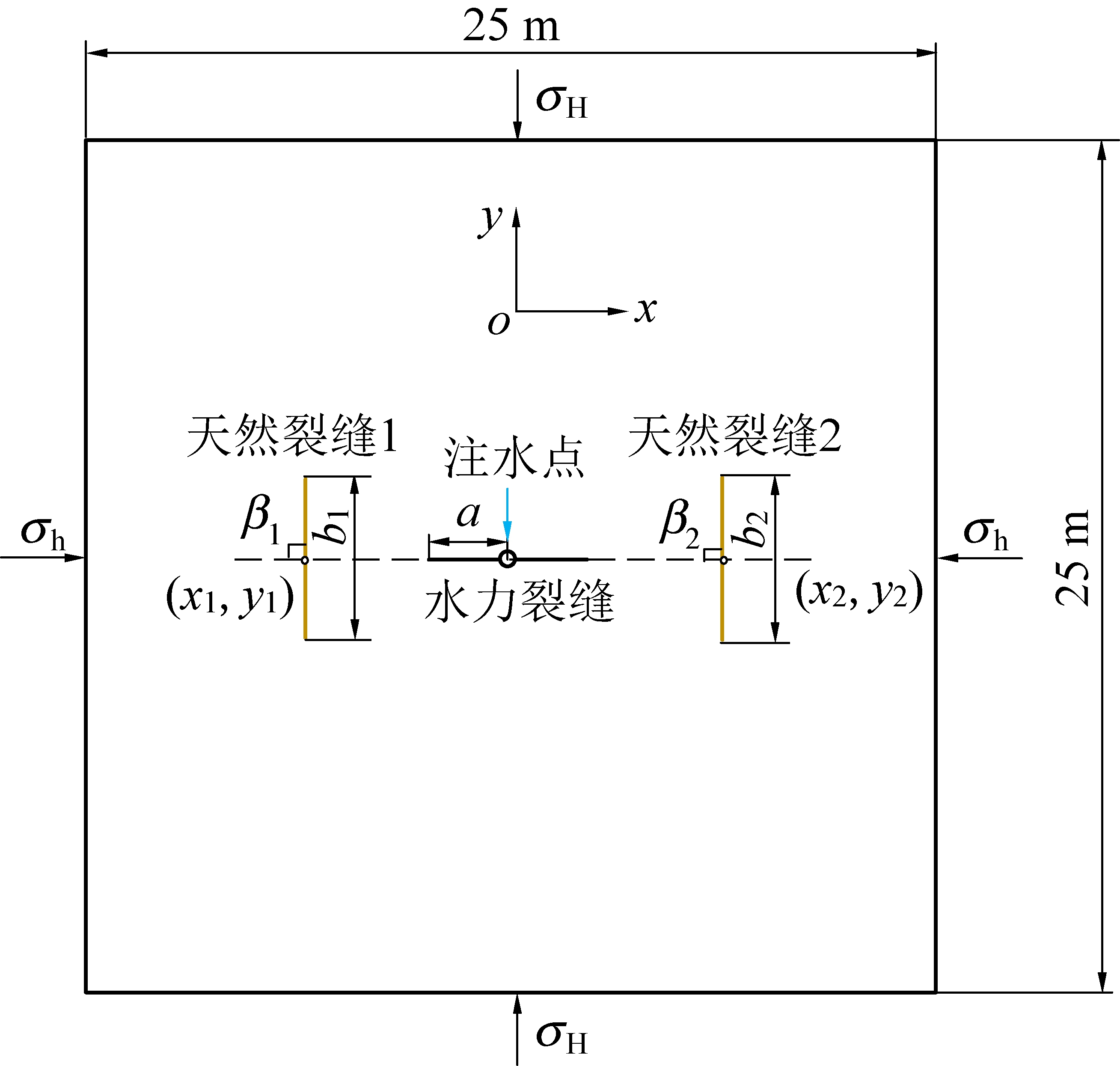
图6 计算模型1示意
Fig.6 Schematic of calculation model 1
长a=2 m,压裂液注入速率为Q0。2条天然裂缝沿y轴布置在水力裂缝两侧,其中心点坐标(x1、y1)和(x2、y2)分别为(-4,0)和(4,0),长度b1=b2=4 m,裂缝相交角β1=β2=90°,模型具体参数取值如下:

最大水平主应力σH/MPa4,5,6,7最小水平主应力σh/MPa4岩石基质弹性模量E/MPa20岩石基质泊松比ν0.25岩石基质断裂韧度KIC/(MPa·m1/2)0.5岩石基质抗拉强度T0/MPa2天然裂缝摩擦因数μf0.69天然裂缝黏结力C/MPa1压裂液注入速率Q0/(m2·s-1)0.001压裂液黏度μ/(Pa·s)0.1
σh=4 MPa、σH=4 MPa,应力差为0时前3个压裂步的水力压裂裂缝扩展应力云图如图7所示。随着压裂液的注入,当t=2.14 s时水力裂缝开始在水压和地应力共同作用下,沿最大主应力方向(水平方向)向两翼扩展,如图7a、图7d、图7g所示。

图7 不同注水时间下水力压裂裂缝扩展应力(σxx、σyy和σxy分别表示x方向应力、y方向应力及剪应力)
Fig.7 Contours of stress of hydraulic fracturing crack propagation at different injection time (σxxstress in x direction,σyystress in y direction,σxyshear stress)
t=8.35 s时水力裂缝与天然裂缝相交,此时储层应力状态发生明显的变化。如图7b、图7d、图7h所示,x方向应力减小,y方向应力和剪应力增大(本文应力为正值时表示拉应力)。水力裂缝两侧的压应力减小,水力裂缝与天然裂缝相交点处出现x方向应力、y方向应力与剪应力集中区,同时天然裂缝两尖端均有较大的y方向应力与剪应力产生。图7c、图7f、图7i为水力裂缝与天然裂缝相交后沿天然裂缝两端扩展情况,可知水力裂缝贯通天然裂缝后沿天然裂缝两端继续沿储层基质传播,裂缝相交点和裂缝尖端均有较大的剪应力产生。
4种水平应力差水平下水力压裂裂缝最终扩展路径分布如图8a所示,A-F为Δσ=3 MPa时每一破裂步的裂缝扩展位置,A点为第1次裂缝扩展的裂尖位置。随着水平应力差的减小,与天然裂缝相交后裂缝沿天然裂缝两端继续扩展的裂缝路径由水平方向逐渐向垂直方向倾斜,向最大主应力方向偏转。
由图8b可知当水平应力差Δσ分别为0、1、2和3 MPa时,裂缝起裂压力p0分别为5.93、6.93、7.94和8.93 MPa,可知裂缝的起裂压力随水平应力差线性增加。水力裂缝未与天然裂缝相交前,注水点压力从裂缝起裂A点开始逐渐减小,水力裂缝与天然裂缝在B点相交,但此时水力裂缝中的压裂液还未与天然裂缝直接沟通,C点为水力裂缝沟通天然裂缝并沿天然裂缝两端传播得到的裂缝裂尖,此时注水点净水压力快速降低了0.46 MPa。这是由于天然裂缝黏结力较低,当水力裂缝与天然裂缝相交,发生天然裂缝张开行为时,压裂液快速贯通天然裂缝,使得注水水压出现骤降现象。

图8 水平应力差对裂缝扩展以及注水压力的影响
Fig.8 Effect of horizontal differential stress on crack propagation and water injection pressure horizontal stress differences
3.2 天然裂缝相交角与长度对裂缝扩展的影响
为研究天然裂缝相交角对水力压裂裂缝扩展的影响,模拟计算了在最大水平主应力σH=4 MPa和最小水平主应力σh=2 MPa时,天然裂缝相交角β分别为45°、60°和75°的水力压裂裂缝扩展数值实验。为简化计算,本节分析水力裂缝单翼扩展与单天然裂缝相交扩展的对称模型如图9所示。其中模型原点位于左下角,注水点坐标(0,12.5)水力裂缝沿水平方向x布置,其长度a=2.5 m天然裂缝长度b=4 m,天然裂缝中点坐标为(8.5,12.5),模型其他参数见上文。

图9 计算模型2示意
Fig.9 Schematic of calculation model 2
为更加清楚描述天然裂缝相交角大小与天然裂缝长度对水力压裂效果的影响。对于本文中二维水力压裂裂缝扩展模型,引入压裂裂缝面积Sf,对裂缝宽度和长度进行量化描述。其中压裂裂缝面积Sf计算公式为
Sf=![]() wids
wids
(13)
式中:s=0处为注水点位置,s=l为压裂裂缝末端尖位置;wi为第i个裂缝计算点的裂缝宽度。
由图10a可知天然裂缝与水力裂缝相交后天然裂缝上端裂尖停止向岩石基质传播,仅沿天然裂缝下端继续传播。可知天然裂缝上段靠近水力裂缝,受水力裂缝产生的诱导应力影响作用明显,使得天然裂缝上端裂尖停止向岩石基质传播。而天然裂缝下段离水力裂缝较远,受其产生的诱导应力影响较小,天然裂缝下端裂尖可继续扩展。
裂缝宽度与长度变化规律如图10b所示,可知:①水力裂缝A点与天然裂缝相交B点,裂缝宽度逐渐减小,3种相交角度下的裂缝宽度减小趋势相同,相交角越大AB段裂缝宽度越大。②天然裂缝BD段,裂缝宽度出现不连续变化,从相交点B到天然裂缝端D宽度先增大后减小。由4.1节可知,水力裂缝与天然裂缝相交点周围出现应力集中区,因此天然裂缝段宽度分布受到限制,使得裂缝相交处的裂缝宽度出现间断变化,容易造成压裂液流动困难,支撑剂堵塞等情况。由图10b可知裂缝相交角越大限制作用越强,间断现象越明显。③D点之后为沿天然裂缝下端扩展的裂缝,其宽度分布先增大后逐渐减小为0,相交角越小裂缝宽度越大。3种相交角45°、60°和75°最终得到的压裂裂缝长分别为24.15、23.46和22.12 m,压裂面积Sf分别为0.312 7、0.301 7和0.283 6 m2。可知随着天然裂缝相交角度的增大,水力压裂总裂缝长度与压裂面积都随之减小。

图10 天然裂缝相交角的影响
Fig.10 Effect of intersection angle of natural crack
同时研究了天然裂缝长度对裂缝扩展的影响,分别计算了天然裂缝长度为b=6、8 和10 m三种情况下水力压裂裂缝扩展情况,天然裂缝相交角设置β为60°,其他模型参数取值与上一算例相同。从图11a可知3种天然裂缝长度下,水力裂缝与天然裂缝相交后裂缝扩展路径相似,最终获得的裂缝长度分别为25.77、25.78、25.78 m,差别很小,即天然裂缝长度对水力压裂总裂缝长度影响不大。但天然裂缝长度影响最终的裂缝宽度分布,天然裂缝长度的增加,裂缝相交前AB段裂缝宽度逐渐减小,3种天然裂缝长度下的宽度减小趋势相同。同时随着天然裂缝的增大天然裂缝BD段宽度限制作用逐渐增大,D点之后的裂缝宽度越小。由图11b可知3种长度下最终的压裂裂缝面积Sf分别为:0.442 5、0.353 1和0.306 5 m2。随着天然裂缝长度的增加,压裂裂缝面积逐渐减小。
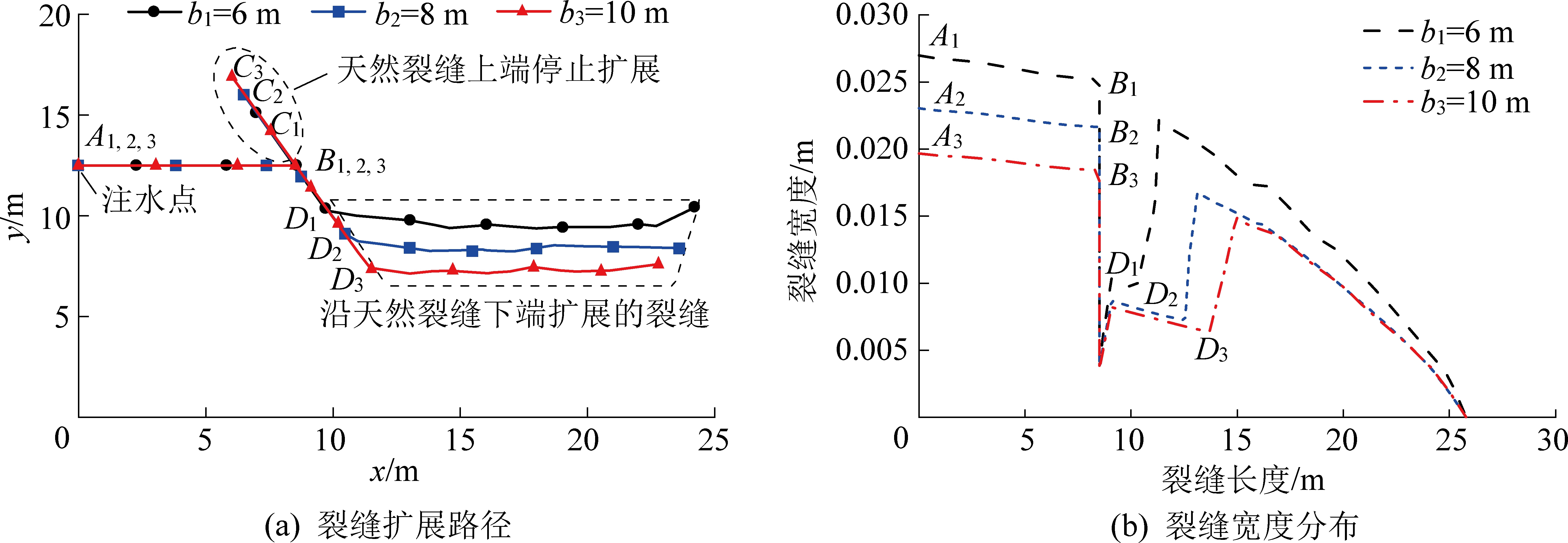
图11 天然裂缝长度的影响
Fig.11 Effect of length of natural crack
4 结 论
在考虑岩石储层基质变形,裂缝内的流体流动以及天然裂缝与水力裂缝的相交作用情况下建立了二维水力压裂裂缝相交扩展模型,研究分析了水平应力差、天然裂缝相交角和天然裂缝长度对水力压裂过程中发生水力裂缝与天然裂缝相交扩展时裂缝扩展变化的规律,得出以下结论:
1)随着水平应力差的线性增加,裂缝起裂注水压力呈线性增大趋势。水平应力差对水力裂缝与天然裂缝相交后的裂缝扩展路径有显著影响,裂缝逐渐向最大主应力方向偏转。
2)水力裂缝与天然裂缝相交时,注水点水压出现骤降现象,裂缝相交点处易出现应力集中区,天然裂缝段宽度受到限制作用,裂缝相交处宽度出现间断现象。
3)天然裂缝相交角影响压裂裂缝长度、宽度和面积。天然裂缝相交角越大,裂缝相交点前裂缝宽度越大,而裂缝相交点后的裂缝宽度变的越小,裂缝相交处宽度间断现象越明显。最终的压裂裂缝长度和压裂裂缝面积也越小。
4)天然裂缝长度对压裂裂缝长度影响较小,但对压裂裂缝的宽度和面积影响明显。天然裂缝长度越长,裂缝相交点前裂缝宽度越小,裂缝相交点后的裂缝宽度也越小,压裂裂缝面积越小。
[1] LI Quanshu,XING Hulin,LIU Jianjun,et al. A review on hydraulic fracturing of unconventional reservoir [J].Petroleum,2015,1(1):8-15.
[2] ECONOMIDES M J,Nolte K G. Reservoir stimulation [M].3rd . New Jersey:John Wiley Sons,Ltd,2002.
[3] 刘 顺,何 衡,赵倩云,等.水力裂缝与天然裂缝交错延伸规律[J].石油学报,2018,39(3):320-326.
LIU Shun,HE Heng,ZHAO Qianyun,et al. Staggered extension laws of hydraulic fracture and natural fracture[J]. Acta Petrolei Sinica,2018.39(3):320-326.
[4] WARPINSKIN R,TEUFEL W. Influence of geologic discontinu-ities on hydraulic fracture propagation[J].Journal of Petroleum Technology,1987,39(2):209-220.
[5] LIANG Chao,JIANG Zaixing,ZHANG Chuming,et al. The shale characteristics and shale gas exploration prospects of the lower Silurian Longmaxi shale,Sichuan Basin,South China[J]. Journal of Natural Gas Science and Engineering,2014(21):636-648.
[6] LAMONT N,JESSEN F W .The effects of existing fractures in rocks on the extension of hydraulic fractures[J].Journal of Petroleum Technology,1963,15(2):203-209.
[7] 王 磊,梁卫国.超临界CO2压裂下煤岩体裂缝扩展规律试验研究[J].煤炭科学技术,2019,47(2):65-70.
WANG Lei,LIANG Weiguo. Experimental study on crack propagation of coal-rock mass under supercritical CO2 fracturing[J].Coal Science and Technology,2019,47(2):65-70.
[8] 刘正和,杨录胜,廉浩杰,等.砂岩钻孔轴向预制裂缝定向压裂试验研究[J].煤炭学报,2019,44(7):2057-2065.
LIU Zhenghe,YANG Lusheng,LIAN Haojie,et al.Experimental study of directional fracturing in sandstones with pre-fabricated cracks in the axial direction of borehole[J].Journal of China Coal Society,2019,44(7):2057-2065.
[9] BLANTON T L. An experimental study of interaction between hydraulically induced and pre-existing fractures[C]//Proceedings of the SPE unconventional gas recovery symposium,Society of petroleum engineers,1986:559-571.
[10] GU Hongren,WENG Xiaowei,LUND Jeffrey,et al.Hydraulic fracture crossing natural fracture at nonorthogonal angles:a criterion and its validation[J].SPE Production and Operations,2012,27(1):20-26.
[11] 朱宝存,唐书恒,颜志丰,等.地应力与天然裂缝对煤储层破裂压力的影响[J].煤炭学报,2009,34(9):1199-1202.
ZHU Baocun,TANG Shuheng,YAN Zhifeng,et al. Effects of crustal stresses and natural fractures on fracture pressure of coal reservoirs[J].Journal of China Coal Society,2009,34(9):1199-1202.
[12] KHOEI A R,HIRMAND M,WAHAB M,et al. An enriched FEM technique for modeling hydraulically driven cohesive fracture propagation in impermeable media with frictional natural faults:Numerical and experimental investigations [J].International Journal for Numerical Methods in Engineering,2015,104(6):439-468.
[13] DAHI Taleghani A,OLSON JE. Numerical Modeling of ultistran-ded Hydraulic Fracture Propagation:accounting for the interaction between induced and natural fractures [J].SPE Journal,2011,16(3):575-581.
[14] KESHAVARZI R,MOHAMMADI S.A new approach for nume-rical modeling of hydraulic fracture propagation in naturally fractured reservoirs[C]//Proceedings of SPE/EAGE European Unconventional Resources Conference and Exhibition-From Potential to Production.Vienna,Austria,2012:1-12.
[15] KHOEI A R,VAHAB M,HIRMAND M. Modeling the interaction between fluid-driven fracture and natural fault using an enriched-FEM technique[J].International Journal of Fracture,2016,197(1):1-24.
[16] SHI Fang,WANG Xiaolong,LIU Chuang,et al. An XFEM-based method with reduction technique for modeling hydraulic fracture propagation in formations containing frictional natural fractures[J].Engineering Fracture Mechanics,2017,173:64-90.
[17] 王小龙.扩展有限元法应用于页岩气藏水力压裂数值模拟研究[D].合肥:中国科学技术大学,2017.
[18] BATCHELOR G K. An Introduction to Fluid Dynamics[M].London:Cambridge University Press,1987.
[19] ERDOGAN F,SIH G C. On the crack extension in plates under plane loading and transverse shear[J].Basic Eng-Trans ASME 1963,85:525-527.
[20] GEERSMA J,KLERK F D.A rapid method of predicting width and extent of hydraulically induced fractures[J].Journal of Petroleum Technology,1969,21(12):1571-1581.
