0 引 言
岩石蠕变扰动问题是影响地下岩体工程顺利进行以及后期安全运营的重要问题之一,随着地下岩体工程埋深及规模越来越大,岩体的应力应变状态越来越复杂,部分岩体对外界扰动十分敏感,极易因扰动产生相应的蠕变,导致岩体破坏,给工程岩体的支护和返修带来难题。由岩石蠕变扰动效应强度极限邻域相关理论可知:处于强度极限邻域内的岩石,在外界扰动条件下易产生相应的蠕变变形;处于强度极限邻域外的岩石,在外界扰动条件下不易产生相应的蠕变[1-2]。因此开展岩石蠕变扰动效应相关试验研究,掌握强度极限邻域、其划分依据及蠕变扰动相关规律是预防和解决问题的关键。高延法等[1-2]提出了岩石蠕变扰动效应及强度极限邻域等概念,并进行了相关试验研究,研究表明:强度极限邻域分为左邻域和右邻域,可初步认为左邻域为岩石的长期强度至岩石的单轴抗压强度极限值,在此研究基础上众多学者对岩石蠕变扰动效应这一课题展开了研究。文献[3-5]分别研制了RRTS-I至RRTS-Ⅲ型岩石流变扰动效应试验仪和试验系统。范庆忠[6]进行了岩石蠕变扰动效应单轴、三轴压缩试验和岩梁弯曲蠕变扰动效应试验,得到了岩石的非线性蠕变特征、对扰动荷载敏感的邻域以及强度极限邻域内的蠕变扰动效应。崔希海等[7-8]利用自主研发的常载三轴扰动流变仪和MTS试验系统对2种较典型的岩石(红砂岩和软弱泥岩)进行岩石压缩流变、岩石压缩扰动流变和岩石拉伸扰动流变试验,得出岩石扰动流变的应变远大于同应力下的瞬时应变和流变应变,且每一扰动均产生相应的应变突变,并通过对试验结果的数值分析,建立起以应力状态和扰动载荷及时间为自变量的扰动流变本构方程。付志亮[9]应用新研制的三轴蠕变扰动仪、MTS和弯曲试验仪进行了岩石低围压分级加载条件下的三轴压缩蠕变试验和三轴蠕变扰动效应试验,得出围压对岩石的强度、破坏形态以及横向、轴向蠕变有明显影响,以及在围压相同情况下,岩石的蠕变损伤与扰动冲击荷载能量有关的结论。王波等[10-11]进行了岩石蠕变扰动效应单轴压缩试验,得出强度极限邻域内岩石蠕变对外界扰动响应明显,扰动产生的蠕变扰动变形量剧烈增加且不可恢复,随着扰动能量的累积,蠕变加速增长至试件破坏,并根据试验结果,绘制了不同流变阶段的累计扰动变形量-累积扰动能量曲线,结合岩石流变扰动的影响因素,在流变扰动曲线的基础上建立了岩石流变扰动本构方程。黄万朋[12]开展了深井巷道变形机理与围岩流变变形控制研究,分析了深部巷道围岩破坏机理与支护体的作用机理,理论推导出了巷道围岩保持长期稳定所需要的支护反力的计算公式。王军等[13]进行了钢管混凝土组合支架支护技术研究,通过有限元分析、理论计算和二次流变扰动试验,验证了组合支架承载力基本满足动压扰动作用下的围岩稳定需求,并设计出基于钢管混凝土组合支架的交岔点返修支护方案。此外大量学者[14-15]开展了岩石蠕变特性相关研究,并得到了岩石在单轴压缩条件下的蠕变变化规律以及岩石的非线性蠕变变化特征。但上述研究均未关注扰动条件对蠕变的影响。文献[16]以红砂岩为研究对象进行岩石单轴压缩蠕变试验,试验结果表明由轴向稳定蠕变和横向稳定蠕变所确定的岩石长期强度存在较大差异。长期强度的判定可能直接影响到强度极限邻域的划分,以上有关强度极限领域范围的研究中,均未针对轴向蠕变和横向蠕变所确定的岩石长期强度存在差异这一问题,结合岩石蠕变扰动效应相关理论对强度极限邻域进行对比研究。此外以往有关强度极限邻域的研究,多关注瞬时扰动变形量,对扰动后的残余扰动变形量转化规律研究较少。针对以上问题,应用自主研发的RRTS-IV型岩石蠕变扰动效应试验系统,及配备的动态测试分析系统进行岩石蠕变及其扰动效应下红砂岩单轴压缩试验,开展强度极限邻域的相关研究,得到合适的强度极限邻域及其划分依据,进一步丰富岩石蠕变扰动效应相关研究。
1 岩石蠕变试验系统及试件
试验应用自主研发的RRTS-IV型岩石蠕变扰动效应试验系统,和购置的东华动态测试分析系统,进行岩石蠕变及其扰动效应单轴压缩试验,开展强度极限邻域相关研究。岩石蠕变扰动效应试验系统主要包括试验仪主机、冲击扰动装置、逐级加载装置;动态测试分析系统主要包括DH5922N动态信号分析仪、DH3810N-1应变适调器、YLR-3F压力传感器等。试验选取红砂岩为研究对象,从同一块较大母岩上取ø50 mm×100 mm红砂岩试件若干,经声波检测后,选取其中波速差异性较小的6个试件进行分组试验,其中试件2、3、4进行岩石单轴压缩常规试验,试件1、5、6进行岩石蠕变及其扰动效应下红砂岩单轴压缩试验。
2 岩石单轴压缩常规试验
将准备好的岩石试件2、3、4依次放置到RMT试验机上进行岩石单轴压缩常规试验,测得岩石的单轴抗压强度及轴向和横向应变。试验结果见表1,其平均单轴抗压强度值为62.76 MPa,平均轴向应变为6.935×10-3;由于横向位移传感器探头与试件接触部分发生劈裂,造成横向应变偏差较大,故未取横向应变平均值作为后续试验研究依据。
表1 岩石单轴压缩常规试验数据
Table 1 Conventional test data of rock uniaxial compression
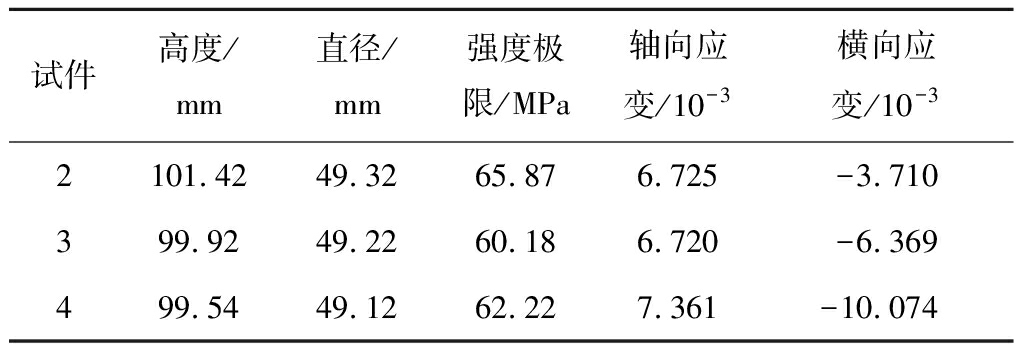
试件高度/mm直径/mm强度极限/MPa轴向应变/10-3横向应变/10-32101.4249.3265.876.725-3.710399.9249.2260.186.720-6.369499.5449.1262.227.361-10.074
注:应变中正号代表轴向变形;负号代表横向变形。
3 单轴压缩试验过程及结果分析
3.1 试验过程及步骤
岩石蠕变及其扰动效应下红砂岩单轴压缩试验共进行了3次,采用分级增量的加载方式,依据之前岩石单轴压缩常规试验测得的平均单轴抗压强度62.76 MPa,试件1、5、6拟选取15、20、25、30、35、40、45、50、55、60 MPa等10个蠕变应力等级,进行岩石单轴压缩蠕变及其扰动效应试验,每级蠕变时间约14 h。试验开始时先进行预加载,调整试件和仪器,使对称的2个应变片的读数大致相同,然后进行正式的蠕变应力等级加载。依据事先设定好的蠕变应力等级依次进行加载,加载速度控制在300~500 N/s,当第1级蠕变变形趋于稳定后,进行扰动,每次扰动进行10次冲击,每次冲击间隔30 s,冲击高度10 cm,冲击砝码质量1.5 kg,10次冲击完成后,让试件在这一蠕变应力等级下继续蠕变100~150 min,以便观察冲击后的蠕变变形规律。以上操作完成后即可进行下一蠕变应力等级的蠕变扰动效应试验,蠕变稳定后进行冲击扰动,如此循环直至试件破坏。试验共进行了10次蠕变应力等级加载,9次扰动,试件在蠕变应力等级60 MPa条件下未进行冲击扰动就提前发生蠕变破坏,故只进行了9次扰动。
3.2 长期强度分析
三次岩石蠕变及其扰动效应下红砂岩单轴压缩试验的试验结果基本相同,故以试件5为例,展开试验结果分析。试验全程蠕变扰动曲线如图1所示。
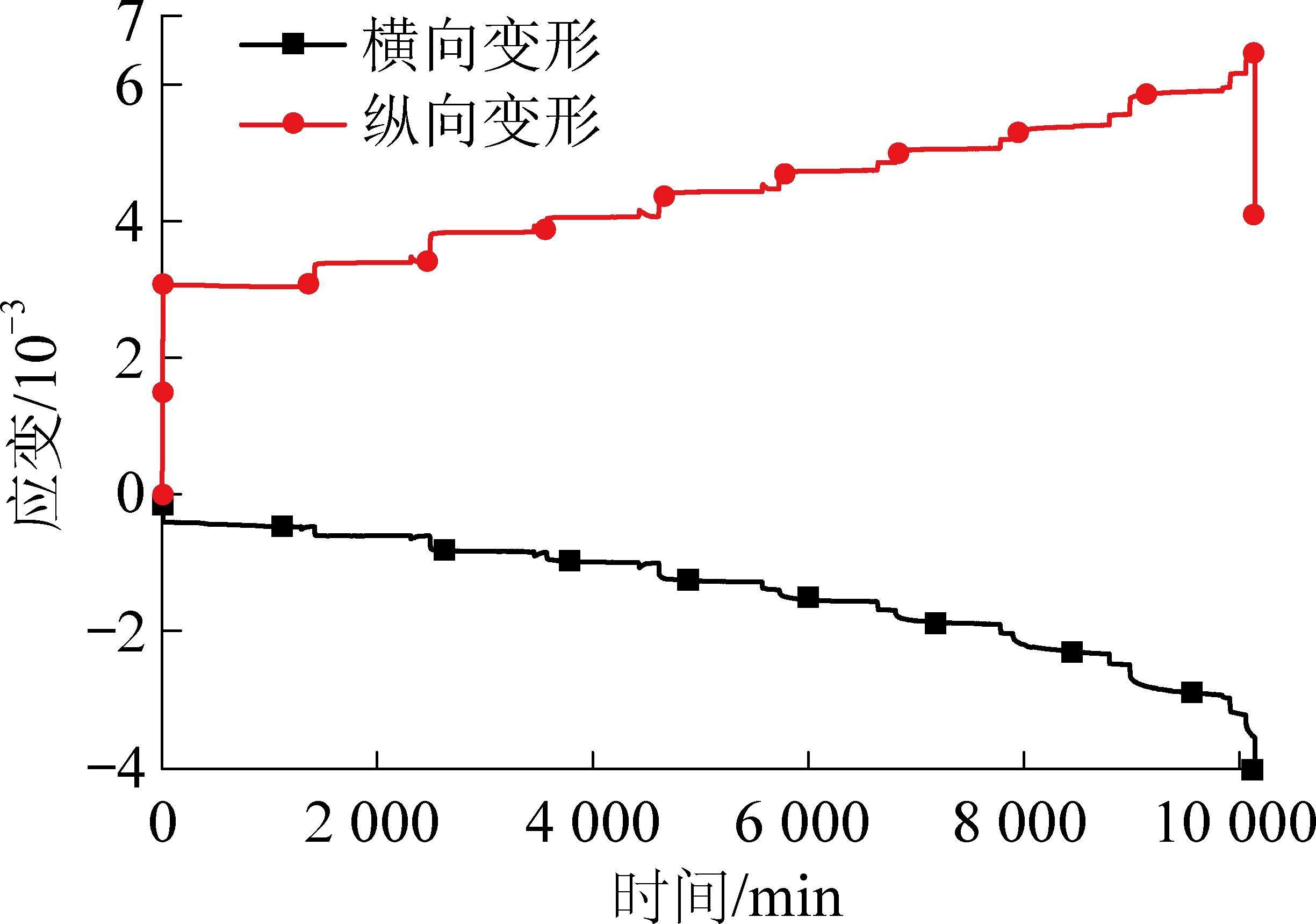
图1 单轴全程扰动蠕变曲线
Fig.1 Uniaxial creep disturbance curve
分级加载蠕变曲线如图2所示,由图2a可知:在应力水平15~30 MPa下,轴向蠕变速率随着时间的增加减速增长,最终趋于一条水平的直线;在应力水平35~55 MPa下,轴向蠕变速率随着时间的增加先减速增长,然后匀速增长,且随着应力水平的提高匀速增长速率逐渐增大;由此可初步判断轴向蠕变确定的长期强度至少为30 MPa。以同样的方式观察图2b,可初步判断横向蠕变确定的长期强度至少为25 MPa。

图2 分级加载蠕变曲线
Fig.2 Creep curve of graded loading
应力-应变等时曲线如图3所示,等时曲线簇大致从线性向非线性、从密集向稀疏演变。随着应力水平的增加曲线离散性和弯曲度越来越大,且时间越长弯曲度越大。结合图3和文献[17-18]分析可知:横向应力-应变等时曲线簇存在2个拐点,分别对应30、35 MPa。应力30 MPa之前曲线基本呈线性,曲线簇离散性较低,此时试件未发生明显蠕变变形;应力30~35 MPa曲线簇离散性开始逐渐增大,且弯曲度增大,此阶段试件开始产生蠕变变形;应力35 MPa以后曲线呈非线性,弯曲度和离散性显著增大,此阶段蠕变变形显著增大,试件内部结构损伤裂缝萌生并迅速发展,一段时间后试件即发生破坏。岩石试件在应力35 MPa之前可保持稳定状态,线性变形及裂纹稳定扩展不会发展为蠕变破坏。因此,岩石横向变形确定的长期强度约为35 MPa。以同样的方式观察图3b,应力45 MPa以后曲线呈非线性,弯曲度和离散性显著增大,从而判断出岩石轴向变形确定的长期强度约为45 MPa。

图3 应力-应变等时曲线
Fig.3 Stress-strain isochronous curve
以上2种分析结果一致,从而得出横向变形确定的长期强度约为35 MPa,轴向变形确定的长期强度约为45 MPa。横向蠕变和轴向蠕变规律相似,应力超过长期强度后,随着时间的延长,最终蠕变都会导致岩石的破坏,故从安全角度考虑,以横向变形确定的长期强度35 MPa为岩石的长期强度。
3.3 强度极限邻域分析
3.3.1 横向累积扰动变形分析
岩石试件在各级蠕变应力等级下的横向累积扰动变形如图4所示,应力15、20、25、30、35 MPa条件下的横向累积扰动变形量随扰动次数的增加减速增长,最终增长速度趋于零,横向累积扰动变形量稳定在某一值,且大致在第7、8次扰动时趋于稳定,这表明在蠕变应力等级较低的情况下,前面的横向累积扰动变形会对后续的扰动变形产生影响,出现硬化现象,此时的横向蠕变对扰动不敏感;应力40、45、50、55 MPa条件下的横向累积扰动变形量随扰动次数的增加先减速增长,然后近似匀速增长,未出现硬化现象,表明此时的横向蠕变对扰动敏感;此外各级扰动的初始横向累积扰动变形量和最终横向累积扰动变形量随着蠕变应力等级的提高而逐渐增大,表明横向蠕变对扰动的敏感程度随蠕变应力等级的提高而增加。
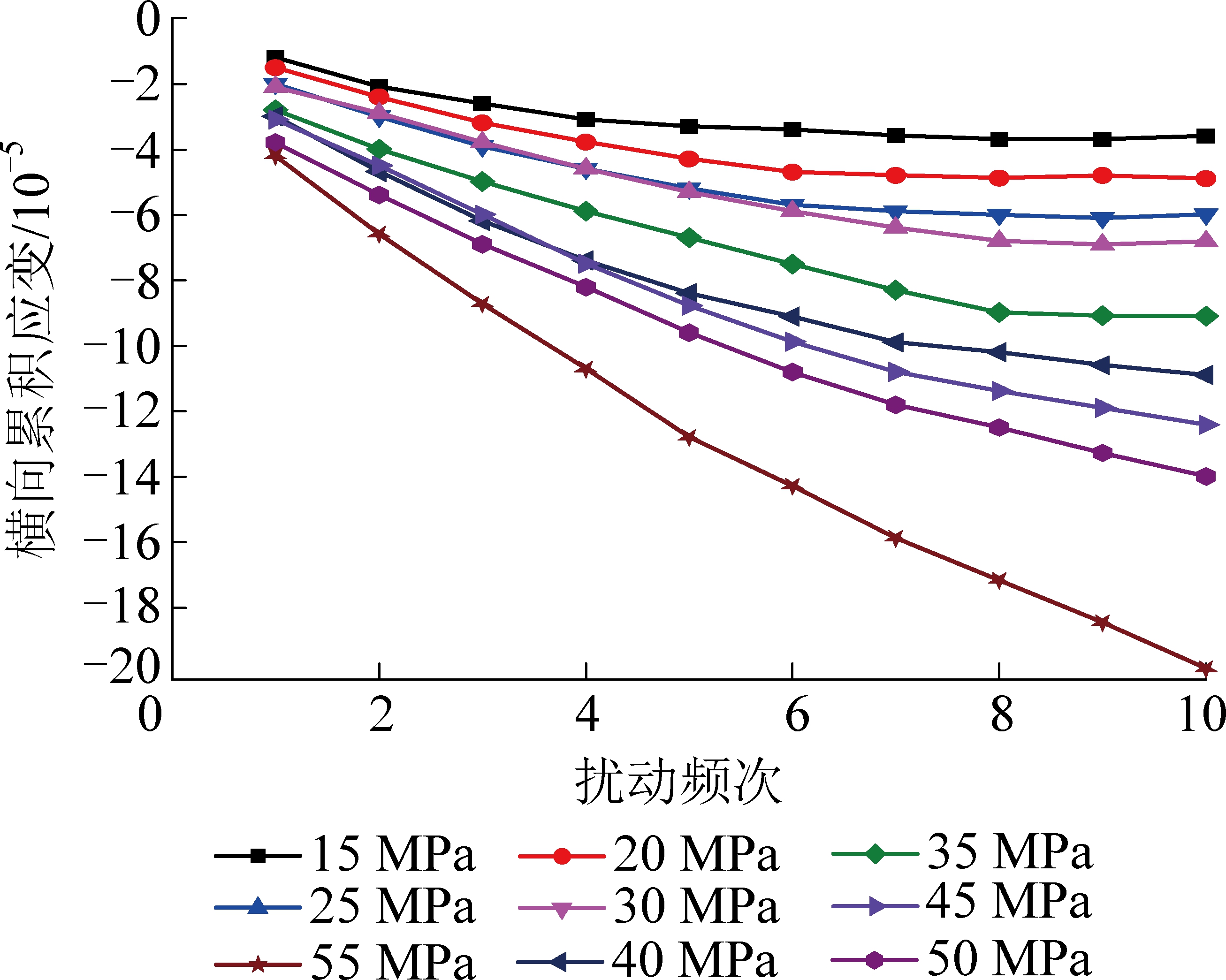
图4 横向累积扰动变形
Fig.4 Transverse cumulative disturbance deformation
3.3.2 轴向累积扰动变形分析
岩石试件在各级蠕变应力等级下的轴向累积扰动变形如图5所示,应力15、20、25、30、35、40 MPa条件下的轴向累积扰动变形量随扰动次数的增加减速增长,最终增长速度趋于0,轴向累积扰动变形量稳定在某一值,且均在第8次扰动时趋于稳定,这表明在蠕变应力等级较低的情况下,前面的轴向累积扰动变形会对后续的扰动变形产生影响,出现硬化现象,此时的轴向蠕变对扰动不敏感;应力45、50、55 MPa条件下的轴向累积扰动变形量随扰动次数的增加先减速增长,然后近似匀速增长,未出现硬化现象,表明此时的轴向蠕变对扰动敏感;此外各级扰动的初始轴向累积扰动变形量和最终轴向累积扰动变形量随着蠕变应力等级的提高而逐渐增大,表明轴向蠕变对扰动的敏感程度随蠕变应力等级的提高而增加。

图5 轴向累积扰动变形
Fig.5 Axial cumulative disturbance deformation
上述横向、轴向累计扰动变形曲线及分析过程中的累计扰动变形量为扰动瞬间产生的变形量累计的结果,以上观测和分析侧重于扰动瞬间产生的瞬时扰动变形量研究。由瞬时扰动变形量确定的横向蠕变和轴向蠕变扰动敏感区存在差异,其中横向蠕变的扰动敏感区为40 MPa至岩石强度极限,横向蠕变的扰动不敏感区为0~35 MPa,过渡区域为35~40 MPa;轴向蠕变的扰动敏感区为45 MPa至岩石强度极限,轴向蠕变的扰动不敏感区为0~40 MPa,过渡区域为40~45 MPa。上述扰动敏感区即强度极限邻域内,扰动不敏感区即强度极限邻域外,过渡区即为强度极限邻域阈值的大致范围。
3.3.3 各级扰动蠕变曲线分析
各蠕变应力等级下的扰动蠕变曲线如图6所示,图6中前11个测点对冲击扰动瞬时变形量进行了描述,之后的所有测点描述了冲击扰动后一段时间内的蠕变规律。由图6可知,15、20、25、30 MPa蠕变应力等级下的横向变形量先在扰动条件下逐渐增加,然后在扰动之后的一段时间内逐渐减小,基本恢复到冲击扰动前的横向变形量,此时的岩石试件处于弹性阶段,冲击扰动产生的瞬时扰动变形量可随着时间的推移逐渐恢复,几乎不产生残余变形量,表明此蠕变应力等级范围下的横向蠕变对扰动不敏感;35、40、45、50、55 MPa蠕变应力等级下的横向变形量先在扰动条件下逐渐增加,扰动完成后,横向变形量未出现减小迹象,而是随时间持续增长,扰动产生大量的残余变形量,表明此蠕变应力等级范围下的横向蠕变对扰动敏感。轴向扰动蠕变变形规律与横向扰动蠕变变形规律基本相似,仅在扰动敏感区范围划分上有所不同,轴向扰动蠕变在应力15、20、25、30、35 MPa条件下,冲击扰动产生的瞬时扰动变形量在之后的蠕变过程中逐渐恢复,几乎不产生残余变形量,表明此蠕变应力等级范围下的轴向蠕变对扰动不敏感;在应力40 MPa条件下,冲击扰动产生的瞬时扰动变形量在之后的蠕变过程中略有回弹,但大部分残余变形保留下来,表明此蠕变应力等级下的轴向蠕变对扰动敏感;轴向扰动蠕变在应力45、50、55 MPa条件下,冲击扰动产生的瞬时扰动变形量未出现回弹现象,扰动产生大量的残余变形量,表明此蠕变应力等级范围下的轴向蠕变对扰动敏感。

图6 各级扰动蠕变曲线
Fig.6 Perturbed creep curves at all levels
上述各级扰动蠕变曲线及上述节分析过程中的残余变形量,为冲击扰动产生的瞬时扰动变形量在之后的蠕变过程中未回弹的部分,即残余扰动变形量。以上观测和分析侧重于扰动后残余扰动变形量转化规律的研究。由此确定的横向蠕变和轴向蠕变扰动敏感区存在差异,其中横向蠕变扰动敏感区为35 MPa至岩石强度极限,横向蠕变扰动不敏感区为0~30 MPa,过渡区域为30~35 MPa;轴向蠕变扰动敏感区为40 MPa至岩石强度极限,轴向蠕变扰动不敏感区为0~35 MPa,过渡区域为35~40 MPa。
3.3.4 综合分析
岩石的破坏是由于内部损伤、裂缝的累积和发展造成的,外部主要表现为应变的增加。综合分析图4—图6可知:在微小扰动条件下,岩石处于低应力水平时,扰动产生的瞬时扰动变形量的累积过程会出现硬化现象(即累积到某值时不再增加),一段时间后瞬时扰动变形量几乎全部恢复,只产生少量残余扰动变形量,即产生少量的不可恢复变形量,几乎不会影响岩石的破坏进程,即此应力状态下的岩石对外界扰动不敏感,处于强度极限邻域外;当应力水平增大到某一值后,扰动产生的瞬时扰动变形量的累积过程也会出现硬化现象,但此时的瞬时扰动变形量大部分会转化为残余扰动变形量,即产生大量的不可恢复变形量,会影响岩石的破坏进程,即此应力状态下的岩石对外界扰动敏感,处于强度极限邻域内;当应力水平继续增大,扰动产生的瞬时扰动变形量的累积过程不再出现硬化现象,且全部转化为残余扰动变形量,即产生大量的不可恢复变形量,对岩石的破坏进程产生更大的影响,即此应力状态下的岩石对外界扰动敏感,处于强度极限邻域内。瞬时扰动变形量是一个瞬时量,具有可恢复性,直接以它为依据判断岩石的破坏进程不准确;瞬时扰动变形量未恢复的部分,即残余扰动变形量,是一个长期变量,可反映岩石的破坏进程。故以扰动后残余扰动变形量转化规律来确定强度极限邻域更合适。各种方式确定的强度极限邻域数据见表2。
表2 强度极限邻域数据
Table 2 Strength limit neighborhood range data

影响因素横向蠕变强度极限邻域划分/MPa轴向蠕变强度极限邻域划分/MPa外过渡区内外过渡区内瞬时扰动0~3535~4040~强度极限0~4040~4545~强度极限残余扰动0~3030~3535~强度极限0~3535~4040~强度极限
横向蠕变残余扰动变形量转化规律确定的强度极限邻域大于轴向蠕变残余扰动变形量转化规律确定的强度极限邻域,即进入强度极限邻域的横向蠕变阈值小于轴向蠕变阈值,横向蠕变先于轴向蠕变进入强度极限邻域,说明横向蠕变相对于轴向蠕变对扰动更敏感。横向蠕变扰动规律和轴向蠕变扰动规律基本相似,一旦进入强度极限邻域,蠕变变形对外界扰动敏感,会因外界扰动而产生相应的瞬时扰动变形量,然后转化为残余扰动变形量,从而导致岩石的破坏;故以横向蠕变残余扰动变形量转化规律确定的阈值界定强度极限邻域,对确保岩体工程长期稳定安全更有意义。由此得出红砂岩的强度极限邻域阈值在30~35 MPa,取平均为32.5 MPa。
由3.2长期强度分析可知:岩石的长期强度约为35 MPa。依据高延法等[1]的相关研究:可初步认为强度极限左邻域为岩石的长期强度至岩石的单轴抗压强度极限值。以长期强度确定的强度极限邻域阈值为35 MPa,以残余扰动变形量转化规律确定的强度极限邻域阈值为32.5 MPa,两者相差约为2.5 MPa,但作为简单的初步分析判定仍有较高的参考价值,要得到准确的强度极限邻域来指导工程实践,需以横向蠕变残余扰动变形量转化规律确定强度极限邻域。
4 结 论
1)相对瞬时扰动变形量,以残余扰动变形量转化规律确定强度极限邻域更合适。低应力条件下,瞬时扰动变形量的累积存在硬化现象,几乎不会转化为残余扰动变形量,即岩石处于强度极限邻域外;随着应力水平的提高,瞬时扰动变形量的累积不再出现硬化现象,大部分或全部转化为残余扰动变形量,即岩石处于强度极限邻域内。
2)横向、轴向蠕变残余扰动变形量转化规律确定的强度极限邻域存在差异,横向蠕变先于轴向蠕变进入强度极限邻域内;以横向蠕变残余扰动变形量转化规律确定强度极限邻域更合适,由此得出红砂岩的强度极限邻域阈值约为32.5 MPa。
3)以长期强度确定的强度极限邻域阈值为35 MPa,以残余扰动变形量转化规律确定的强度极限邻域阈值为32.5 MPa,两者相差约为2.5 MPa,但作为简单的初步分析判定,以长期强度确定强度极限邻域仍有较高的参考价值。
[1] 高延法,范庆忠,崔希海,等.岩石流变及其扰动效应试验研究[M].北京:科学出版社,2007.
[2] 高延法,肖华强,王 波,等.岩石流变扰动效应试验及其本构关系研究[J].岩石力学与工程学报,2008,27(S1):3180-3185.
GAO Yanfa,XIAO Huaqiang,WANG Bo,et al.Rheological test of sandstone with perturbation effect and its constitutive relationship study[J].Chinese Journal of Rock Mechanics and Engineering,2008,27(1):3180-3185.
[3] 崔希海,高延法,李进兰.岩石扰动蠕变试验系统的研发[J].山东科技大学学报,2006,25(3):36-38.
CUI Xihai,GAO Yanfa,LI Jinlan.Research and development of rock creep experimental system under disturbing load[J].Journal of Shandong UnIversity of Science and Technology(Natural Sci-ence),2006,25(3):36-38.
[4] 高延法,马鹏鹏,黄万朋,等.RRTS-Ⅱ型岩石流变扰动效应试验仪[J].岩石力学与工程学报,2011,30(2):238-243.
GAO Yanfa,MA Pengpeng,HUANG Wanpeng,et al.RRTS-II testing machine for rock rheological perterbation effect[J].Chinese Journal of Rock Mechanics and Engineering,2011,30(2):238-243.
[5] 王 波,高昌炎,陈学习,等.岩石流变扰动效应三轴试验系统[J].煤炭学报,2018,43(2):433-440.
WANG Bo,GAO Changyan,CHEN Xuexi,et al.Axial load test study on the perturbation properties of rock rheology[J].Journal of China Coal Social,2017,42(6):1143-1450.
[6] 范庆忠.岩石蠕变及其扰动效应试验研究[D].青岛:山东科技大学,2006.
[7] 崔希海.岩石流变扰动效应及试验系统研究[D].青岛:山东科技大学,2007.
[8] 崔希海,李进兰,牛学良.岩石扰动流变规律和本构关系的试验研究[J].岩石力学与工程学报.2007,26(9):1875-1881.
CUI Xihai,LI Jinlan,NIU Xueliang,et al.Experimental study on rheological regularity and constitutive relationship of rock under disturbing loads[J].Chinese Journal of Rock Mechanics and Engineering,2007,26(9):1875-1881.
[9] 付志亮.岩石蠕变扰动效应与损伤特征理论与试验研究[D].青岛:山东科技大学,2007.
[10] 王 波,高昌炎,陈学习,等.岩石流变扰动特性单轴压缩试验研究[J].煤炭学报,2017,42(6):1443-1450.
WANG Bo,GAO Changyan,CHEN Xuexi,et al.Axial load test study on the perturbation properties of rock rheology[J].Journal of China Coal Social,2017,42(6):1143-1450.
[11] 王 波,高延法,王 军.流变扰动效应引起围岩应力场演变规律分析[J].煤炭学报,2010,9(35):1446-1450.
WANG Bo,GAO Yanfa,WANG Jun,et al.Evolution law analysis on sur-rounding rock stress field by rheology disturbed effects[J].Journal of China Coal Society,2010,35(9):1446-1450.
[12] 黄万朋.深井巷道非对称变形机理与围岩流变及扰动变形控制研究[D].北京:中国矿业大学(北京),2012.
[13] 王 军,黄万朋,左建平,等.深井交岔点围岩流变扰动效应及钢管混凝土组合支架支护技术研究[J].岩石力学与工程学报,2018,2(37):461-472.
WAN Jun,HUANG Wanpeng,ZUO Jianping,et al.Rheological perturbation effect of rock and combined support of concrete filled steel tubes in deep coal mine roadway[J].Chinese Journal of Rock Mechanics and Engineering,2018,2(37):461-472.
[14] GÉRALDINE F,FRÉDÉRIC P.Creep and time-dependent damage in argillaceous rocks[J].International Journal of Rock Mechanics and Mining Sciences,2006,43(6): 950-960.
[15] TSAI L S,HSIEH Y M,WENG M C,et al.Timedependent deformation behaviors of weak sandstones[J].International Journal of Rock Mechanics and Mining Sciences,2008,45(2):144-154.
[16] 崔希海,付志亮.岩石流变特性及长期强度的试验研究[J].岩石力学与工程学报,2006,25(5):1021-1024.
CUI Xihai,FU Zhiliang.Experimental study on rheology properties and long-term strength of rocks[J].Chinese Journal of rock Mechanics and Engineering,2006,25(5):1021-1024.
[17] 张 玉,金培杰,徐卫亚,等.基碎屑岩三轴蠕变特性及长期强度试验研究[J].岩土力学,2016,37(5):1291-1300.
ZHANG Yu,JIN Peijie,XU Weiya,et al.Experimental study of triaxial creep behavior and long-term strength of clastic rock in dam foundation[J].Rock and Soil Mechanics,2016,37(5):1291-1300.
[18] 李良权,徐卫亚,王 伟,等.基于流变试验的向家坝砂岩长期强度评价[J].工程力学,2010,27(11):127-143.
LI Liangquan,XU Weiya,WANG Wei,et al.Estimation of long-term strength for XiangJiaBa sandstone based on creep tests[J].Engineering Mechanics,2010,27(11):127-143.
