0 引 言
在露天开采岩石剥离环节中,由于生产剥采比和生产成本的提高,深孔高台阶抛掷爆破技术得到应用——利用炸药爆炸产生的能量可以将30%~65%的剥离物直接抛掷到采空区,降低1/3以上的剥离成本[1]。预测抛掷爆破效果对充分发挥拉斗铲的生产能力、优化抛掷爆破设计并提高抛掷爆破效率具有重要意义。其中有效抛掷率是衡量爆破后抛掷效果和生产成本的重要指标。
目前,国内学者以抛掷爆破相关数据为基础,通过建立智能化数学模型对爆破效果分析进行预测。李祥龙[2]将BP神经网络预测模型用来预测高台阶抛掷爆破效果,预测结果为爆破参数的优化调整提供参考依据;刘干等[3]利用广义回归神经网络建立有效抛掷率模型,预测结果基本满足工程需求;孙文彬等[4]将BP、RBF、SVM等不同神经网络预测模型的结果进行对比,提高了神经网络在露天矿抛掷爆破效果预测方面的精度;刘希亮[5]采用遗传算法对BP神经网络的初始权值和阈值进行优化,提高了预测结果的准确度;温廷新等[6]则采用遗传算法优化极限学习机(ELM)输入权值矩阵和隐含层偏差,对抛掷爆破进行预测。相关研究大多是通过遗传算法优化神经网络来建立抛掷爆破效果预测模型,在提高模型预测准确度方面展开研究。而由于遗传算法中涉及选择、交叉、变异等操作,其计算复杂程度较高;同时,算法的实现涉及许多依靠经验确定的参数,严重影响预测结果的精度。而粒子群算法(PSO)与之相比,具有算法规则简单易于操作、收敛快、搜索功能完善、鲁棒性高的特点,用于优化神经网络预测模型,容易实现更准确的预测结果[7]。
在常规PSO的基础上采用Sigmoid惯性权重自适应调整和学习因子动态调整的方法,改善了算法的收敛性能、更好地平衡算法的局部和全局搜索能力。运用改进的粒子群算法(IPSO)优化极限学习机(ELM)的初始权值和阈值,建立IPSO-ELM预测模型。根据黑岱沟露天煤矿实际爆破数据,以有效抛掷率和松散系数作为评价因子,对抛掷爆破效果进行预测。并与ELM、遗传算法(GA)优化ELM模型进行对比,论证了IPSO-ELM模型在露天矿抛掷爆破效果预测中的可行性和优越性。
1 抛掷爆破效果影响因素与评价指标
1.1 抛掷爆破效果影响因素
影响抛掷爆破效果的因素很多,包括岩石物理力学性质、节理裂隙发育程度、煤层厚度等地质因素;孔网参数、装药结构、炸药性质、布孔和起爆方式等爆破技术条件;以及钻孔质量、装药质量等现场施工水平。针对特定露天煤矿及固定工艺设备,同地段不同爆区位置爆破体岩层地质条件变化不大视为同质,而且所采用的采掘带宽度、装药结构、布孔和起爆方式、孔径等受所采用的穿孔与采装设备规格影响。因此,抛掷爆破台阶高度、炸药单耗、孔排距、最小抵抗线等爆破因素直接影响抛掷爆破效果。
1)抛掷爆破台阶高度。台阶高度是由上覆岩土层的厚度决定的,它直接影响剥离物的抛掷距离。根据外弹道理论,台阶越高,相对抛掷距离越远,有效抛掷率也就越高,则抛掷到采空区无需挖掘设备处理爆破量就越多[8]。同时依据爆炸压力随作用时间变化的关系[9],台阶高度越大,炮孔中爆炸气体作用时间越长,爆破破碎效果也就越好。
2)炸药单耗。炸药起爆后产生的能量既克服孔壁周围岩体抵抗做功,又需具备足够的剩余能量将破碎岩块抛掷出去。同时,从抛掷距离与炸药单耗关系看,抛掷距离作为有效抛掷率的表征参数,与炸药单耗具有正相关关系[10]。因此,炸药单耗对抛掷爆破效果的好坏起直接且关键作用,在避免增大爆破地震效应与冲炮的前提下,适量增加炸药单耗有利于达到良好的抛掷效果。
3)孔、排距。台阶深孔爆破中孔、排距的大小直接影响炸药爆破能量利用率及岩块破碎抛掷效果,其中过大的孔距使相邻炮孔间岩体破碎不充分,而孔距过小则使相邻孔间岩体破碎过粉碎。另外,排距过大使爆破能量克服排间抵抗做功消耗大,降低破碎岩块获得的初始抛掷动能;而排距过小,则使得排间岩体在爆破能量作用下沿抵抗线方向抛掷过远,造成爆破能量的浪费及单耗徒增[11]。
4)最小抵抗线。依据最小抵抗线原理,在最小抵抗线方向,岩石介质对爆破作用的阻力最小,抛掷距离最远[12]。通过调节药包最小抵抗线的方向可以控制爆破介质抛掷的主要方向。抵抗线过大时,克服岩石抵抗做功需要的能量也就越多,剩余的能量不足以抛掷岩石,从而影响抛掷效果;而当抵抗线过小时,由于爆轰气体过早泄漏,减少爆破有效作用时间,降低破碎效果。因此,选用合理的最小抵抗线有利于提高抛掷爆破效果。
1.2 评价指标
1)有效抛掷率。有效抛掷率是抛掷到采空区无需再倒堆的物料与总物料之比[13],是直接反映抛掷爆破效果的重要因子。有效抛掷率越大,抛入采空区中的剥离物越多,剥离成本也就越低。如图1所示,有效抛掷率为
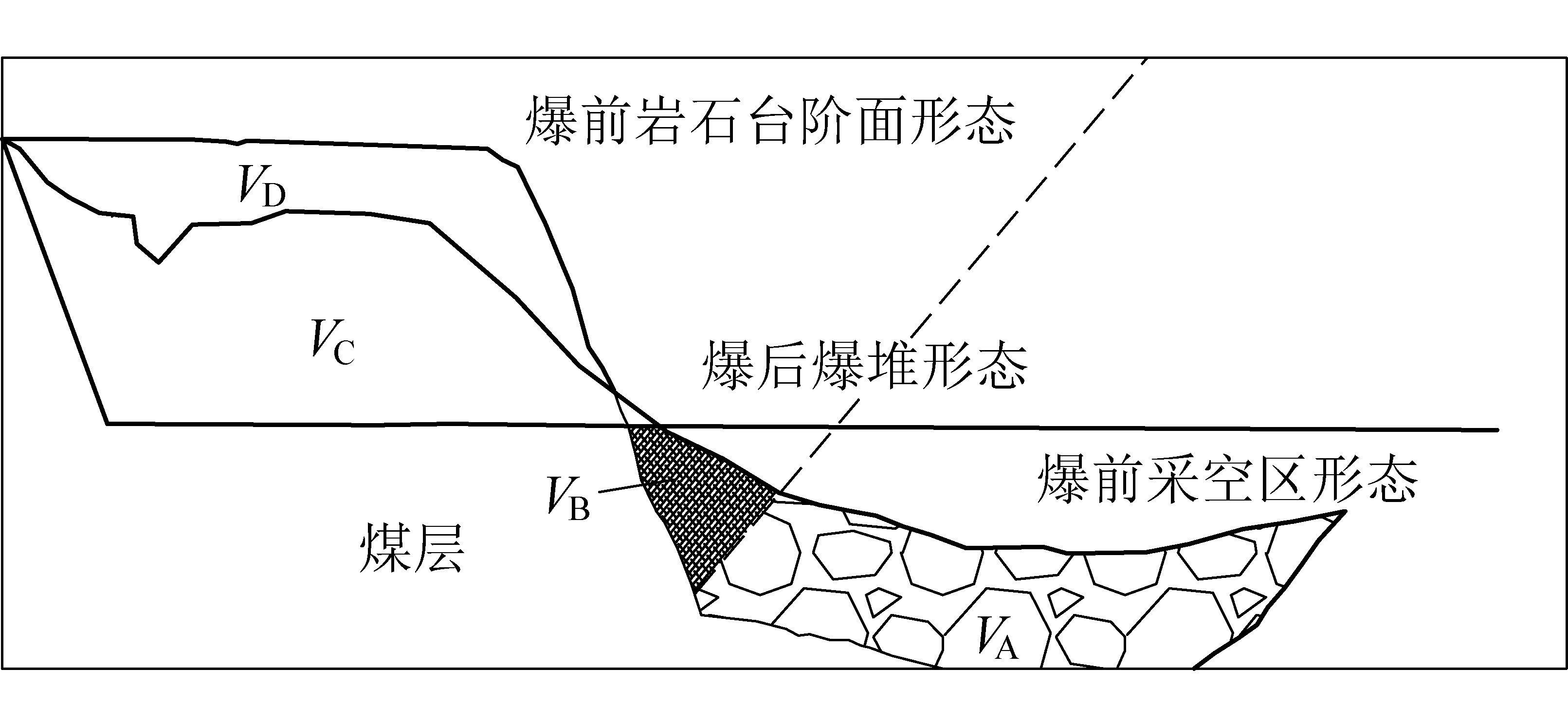
图1 抛掷爆破爆堆形态示意
Fig.1 Schematic diagram of muck pile profile after blast casting
(1)
式中:VA为抛掷到采空区的有效抛掷量,m3;VB为无效抛掷量,m3;VC为未抛掷的爆破量,m3。
2)松散系数。松散系数是爆破后松散体积与爆破前原岩体积的比值[3,13]。松散系数能够直观反映爆破后岩块的破碎程度、爆堆沉降效果,影响拉斗铲及其他辅助工艺设备的作业效率。可表示为
(2)
式中:ks为松散系数;VD为岩石台阶爆破后沉降量,m3。
2 IPSO-ELM模型
2.1 改进的粒子群算法
粒子群算法(PSO)是一种模仿鸟群捕食行为的群体智能优化算法,每只鸟代表的单独粒子表示问题的潜在解,这些粒子在求解空间中不断更新自身的速度和位置、比较适应度值,从而实现个体在整个种群中的寻优[14]。
假设有N个粒子组成的种群X=(X1,X2,…,XN)在一个d维空间中,其中第i个粒子在该空间中的位置和速度分别为
Xi=(Xi1,Xi2,…,Xid)
(3)
Vi=(Vi1,Vi2,…,Vid)
(4)
式中:Xid为第i个粒子位置的d维分量;Vid为第i个粒子速度的d维分量;i=1,2,…,N。
个体极值Pbest是粒子个体在空间搜寻得到的适应度最优位置,群体极值Gbest是种群所有粒子在空间搜寻得到的适应度最优位置,其值分别为
Pbest=(Pi1,Pi2,…,Pid)
(5)
Gbest=(Pg1,Pg2,…,Pgd)
(6)
在不断地迭代更新中粒子产生新的个体极值,将其与群体极值进行比较来更新自身的速度和位置,从而找到最优个体。个体更新公式为
(7)
式中:w为惯性权重;k为当前迭代次数;d为空间维数;![]() 分别为第i个粒子经过第k、k+1次迭代后速度的d维分量;
分别为第i个粒子经过第k、k+1次迭代后速度的d维分量;![]() 分别为第i个粒子经过第k、k+1次迭代后位置的d维分量;Pid为第i个粒子的个体极值的d维分量;Pgd为全局最优位置的第d维分量;c1和c2为加速度因子;r1和r2为分布于[0,1]之间的随机数。
分别为第i个粒子经过第k、k+1次迭代后位置的d维分量;Pid为第i个粒子的个体极值的d维分量;Pgd为全局最优位置的第d维分量;c1和c2为加速度因子;r1和r2为分布于[0,1]之间的随机数。
标准的PSO中,采用线性递减的策略对惯性权重进行调整,局部搜索能力差、收敛过早。而采用基于Sigmoid函数的非线性递减惯性权值法,可以更好地平衡全局和局部搜索能力[15]
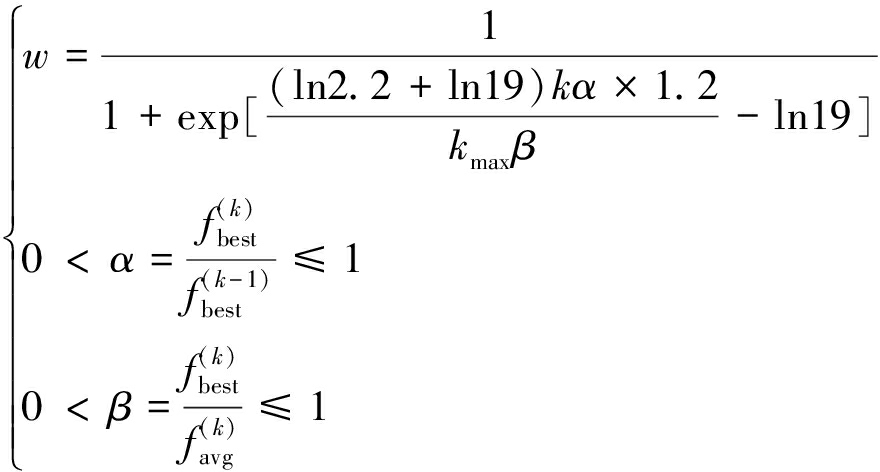
(8)
式中:α为种群进化速度;β为种群聚合度;![]() 为全局极值;
为全局极值;![]() 为当前所有粒子的平均适应值;kmax为最大允许迭代次数。
为当前所有粒子的平均适应值;kmax为最大允许迭代次数。
学习因子c1和c2体现了粒子间信息共享的能力,决定了粒子的运动方向和收敛结果。常规PSO算法中,c1、c2∈[0.5,2.5],不合理的取值导致粒子大量滞留于局部,容易早熟收敛。因此,笔者采用动态调节学习因子的方法,其表达式为[16]
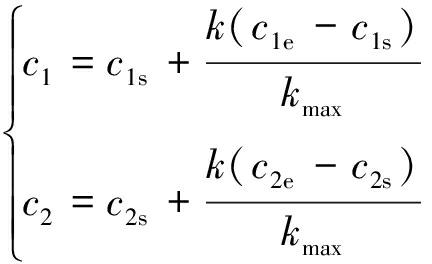
(9)
式中:c1s和c2s分别为c1和c2的初始值;c1e和c2e分别为c1和c2的最终值。
2.2 极限学习机
极限学习机(ELM)是一种单隐含层前馈神经网络(SLFN)的新算法[17],与BP、GRNN等传统算法相比,不需要对训练过程进行调整,只需要依据输入层与隐含层的连接权值及阈值、设置隐含层神经元的个数,就可获得最优解。该算法具有参数设置简单、学习速度快、鲁棒性高等优点[18-19]。
假设输入层有n个神经元,隐含层有l个神经元,输出层有m个神经元。对于Q个训练样本(xj,yj),xj=[xj1 xj2… xjn]T,yj=[yj1 yj2… yjm]T(j=1,2,…,Q)。极限学习机的输入矩阵为X=[x1 x2…xQ],输出矩阵为Y=[y1 y2…yQ]。设隐含层神经元的激活函数为f(x),则神经网络输出为
(10)
式中:wi′为连接输入神经元与第i′个隐含层节点的权值矩阵;βi′为连接第i′个隐含层节点与输出神经元的权值矩阵;bi′为第i′个隐含层节点的阈值矩阵;i′=1,2,…,l。
2.3 IPSO-ELM模型的建立
极限学习机中权值、阈值、隐含层节点个数的设置对预测精度有很大的影响。同时可能存在随机给定的输入权值矩阵和隐含层偏差为0的情况,使得部分隐含层节点失效,导致网络泛化能力降低。而隐含层节点过多,增加网络的复杂程度,容易产生过拟合现象。采用改进的粒子群算法(IPSO)优化ELM的连接权值和偏置阈值,将ELM中的连接权值和偏置阈值作为种群的粒子,用训练样本计算的均方误差作为粒子群算法的适值函数,全局搜寻最优值。IPSO-ELM算法流程如图2所示,其训练步骤如下:
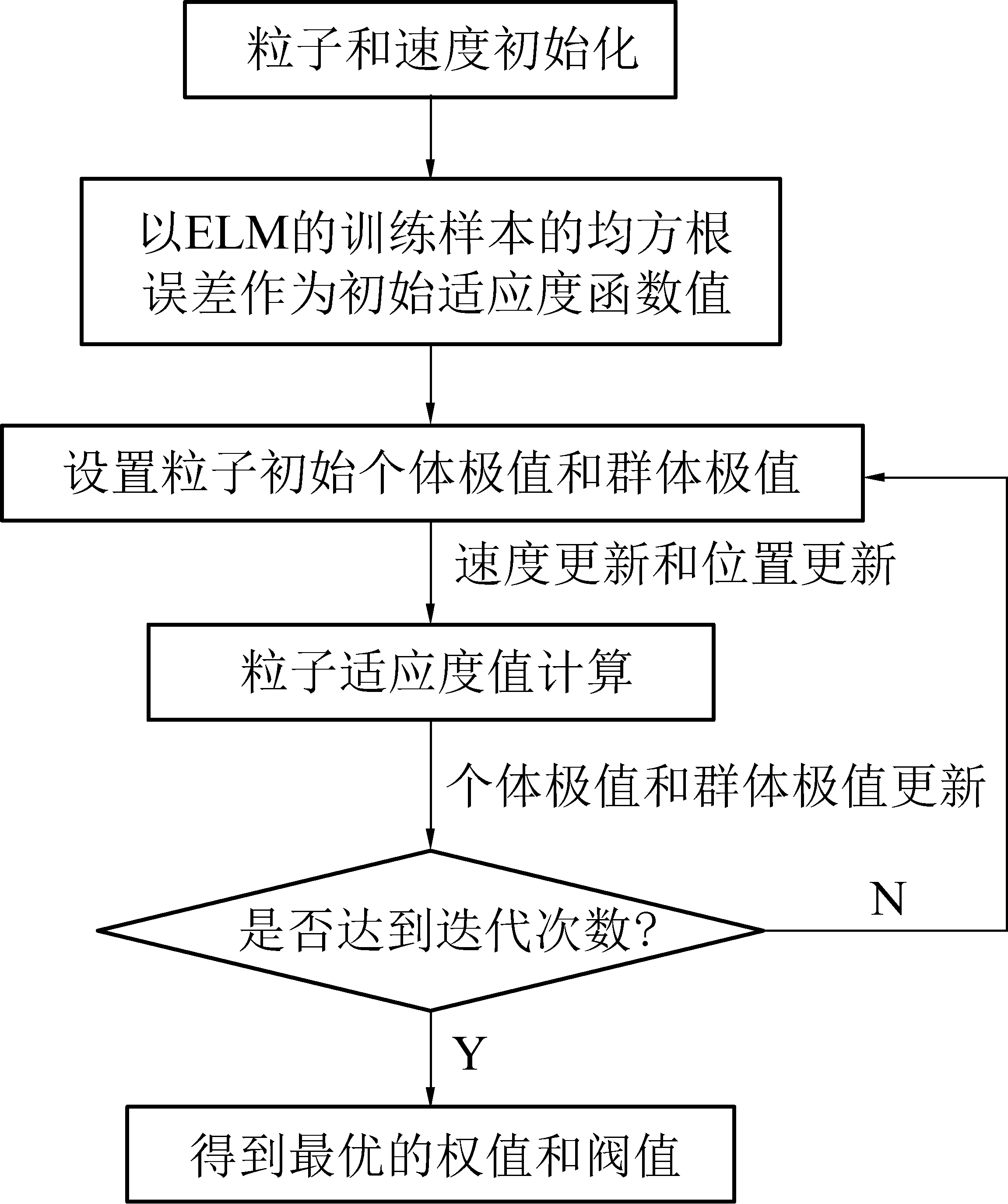
图2 IPSO-ELM算法流程
Fig.2 Flow chart of IPSO-ELM
1)产生种群。根据ELM训练产生的权值和阈值范围设置粒子速度和位置的寻优范围。
2)选择适合的参数。包括种群规模、惯性权重、学习因子、最大迭代次数、粒子维度。
3)根据适值函数,计算出每个粒子的适应度值Fi,求出每个粒子的个体极值Pbest以及全局极值Gbest。从第1个位置开始,将当前粒子的适值与极值进行比较,不断更新个体极值和全局极值。
4)反复循环,对所有粒子的速度和位置进行更新,运行次数达到最大迭代次数即可终止。
5)最佳适应度值对应的粒子即输入层权值矩阵和隐含层偏差,利用ELM算法计算出网络的输出层权值矩阵,即可计算出预测值。
3 IPSO-ELM神经网络模型应用
3.1 IPSO-ELM神经网络训练与测试
建立以炸药单耗、台阶高度、孔距、排距、最小抵抗线为输入因子,有效抛掷率和松散系数为输出因子的预测模型,选取80组数据中的前70组构成训练集,后10组为测试集,对抛掷爆破效果进行预测。部分数据见表1。
表1 IPSO-ELM数据集(部分)
Table 1 IPSO-ELM data set(Part)
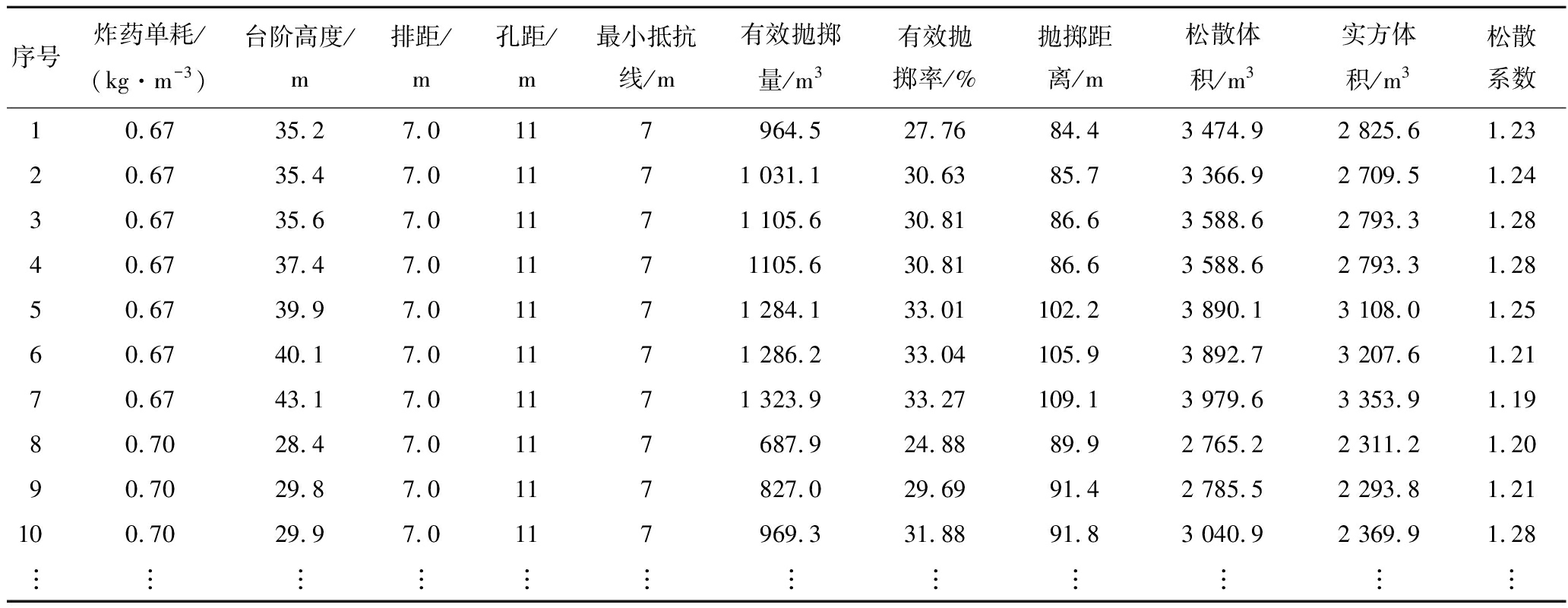
序号炸药单耗/(kg·m-3)台阶高度/m排距/m孔距/m最小抵抗线/m有效抛掷量/m3有效抛掷率/%抛掷距离/m松散体积/m3实方体积/m3松散系数10.6735.27.0117964.527.7684.43 474.92 825.61.2320.6735.47.01171 031.130.6385.73 366.92 709.51.2430.6735.67.01171 105.630.8186.63 588.62 793.31.2840.6737.47.01171105.630.8186.63 588.62 793.31.2850.6739.97.01171 284.133.01102.23 890.13 108.01.2560.6740.17.01171 286.233.04105.93 892.73 207.61.2170.6743.17.01171 323.933.27109.13 979.63 353.91.1980.7028.47.0117687.924.8889.92 765.22 311.21.2090.7029.87.0117827.029.6991.42 785.52 293.81.21100.7029.97.0117969.331.8891.83 040.92 369.91.28︙︙︙︙︙︙︙︙︙︙︙︙
预测模型参数设置如下:粒子收敛寻优的效果与粒子种群规模的大小有关,对复杂难解的问题,粒子数可达100~200,该模型中粒子种群规模取值200;迭代次数40;粒子维度即粒子速度向量的维数,根据模型训练产生的权值和阈值设定为80;采用Sigmoid惯性权重自适应调整和学习因子动态调整方法,得到w范围为[0.80,0.93],c1、c2分别为[1.80,2.25]、[1.70,2.00];运用逐步试算法[20],确定最优隐含层神经元数为11。IPSO与常规PSO在收敛效果方面进行比较,图3反映了目标函数值与迭代次数之间的关系。由此看出,IPSO减少了迭代次数,提高了全局搜索能力,能够更快地找到接近最佳目标的稳定解决方案,性能上的提升见表2。
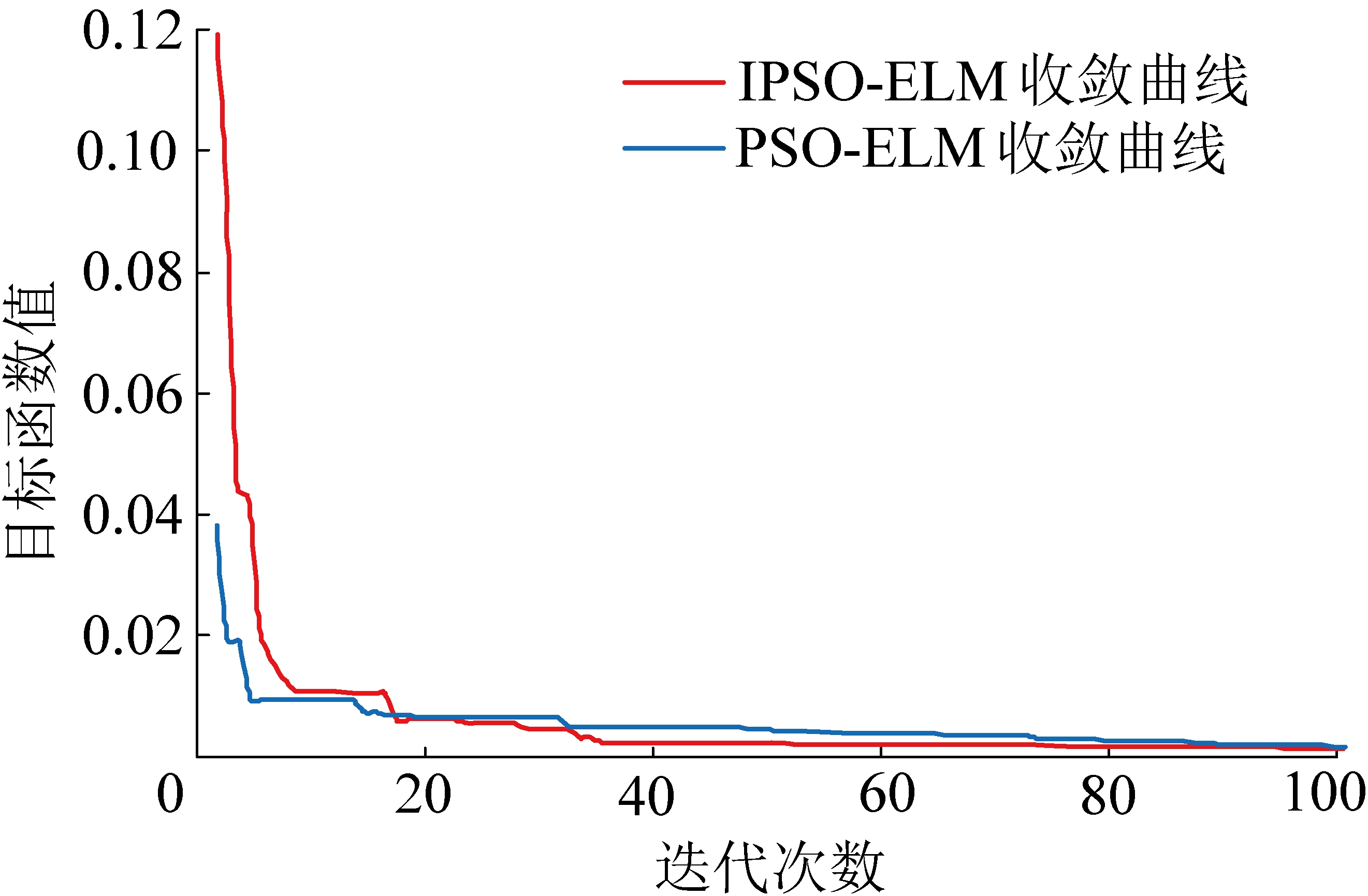
图3 目标函数值与迭代次数关系
Fig.3 Relationship between the value of objective function and number of iterations
表2 IPSO和PSO性能的比较
Table 2 Comparison of algorithm performance of IPSO and PSO

算法迭代次数运行时间/s局部优化次数PSO9132.466IPSO3621.454
采用IPSO-ELM模型对抛掷爆破效果进行预测,预测结果中有效抛掷率的拟合优度R2为0.987 2,松散系数的拟合优度R2为0.991 7。测试结果如图4所示。

图4 IPSO-ELM抛掷爆破效果预测结果
Fig.4 Prediction results of blast casting effects based on IPSO-ELM model
3.2 不同模型预测结果对比分析
为了测试IPSO-ELM预测模型较其他智能算法在露天煤矿抛掷爆破预测方面是否具有优越性。选择ELM模型及文献[6]中建立的抛掷爆破效果GA-ELM预测模型和本文建立的IPSO-ELM模型在抛掷爆破预测结果进行对比,结果如图5所示。
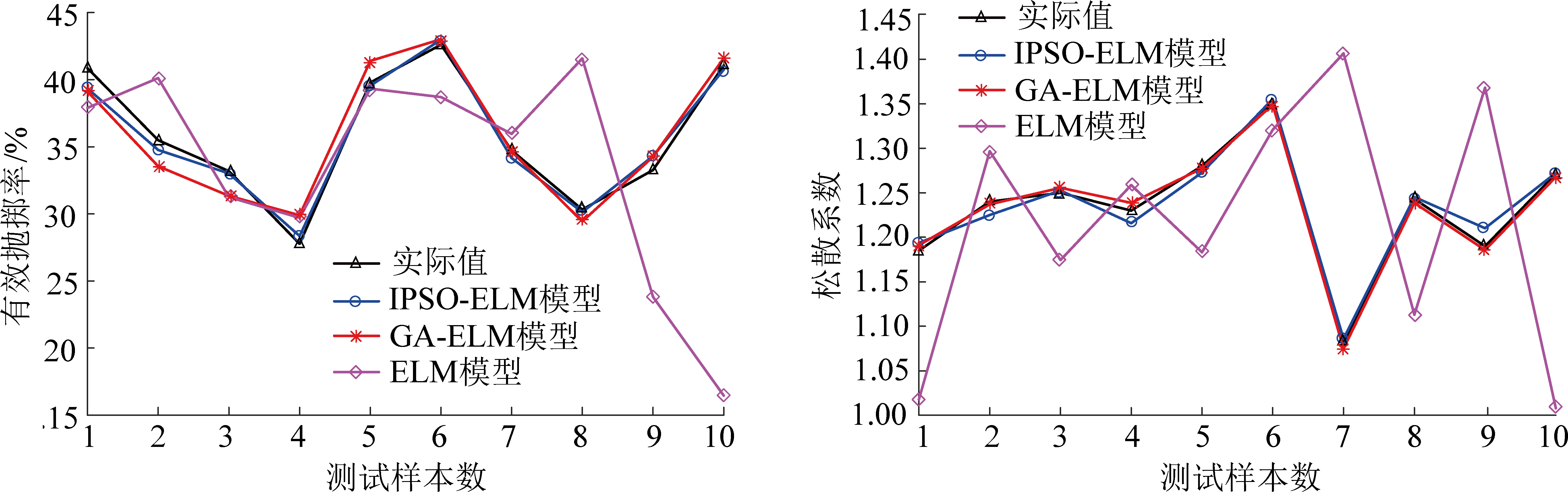
图5 不同神经网络模型预测结果对比
Fig.5 Prediction results comparison of different neural network models
为进一步验证预测模型的性能,从绝对误差(图6)、相对误差(图7)、拟合优度、均方误差、平均绝对误差、平均相对误差、迭代次数(表3)7个对模型的预测精度分别进行具体对比描述。由这些图表可以明显看出,相对单一的神经网络ELM模型,优化算法(GA、PSO)与神经网络相结合可以大幅度提高模型的拟合优度和预测精度。此外与GA-ELM模型相比,IPSO-ELM模型预测结果的R2更接近1。在误差方面,IPSO-ELM预测结果中有效抛掷率的均方误差、平均绝对误差、平均相对误差分别为0.271 4、0.571 3%、0.159 7%,低于GA-ELM的2.167 0、1.213 5%、0.353 1%;松散系数的均方误差、平均绝对误差、平均相对误差分别为1.148 6×10-4、0.004 4、0.360 9%,也低于GA-ELM的2.578 4、0.008 2、0.676 3%。因此,考虑以有效抛掷率和松散系数两种抛掷爆破效果的预测精度和误差的平均值为各模型的R2、均方误差、平均绝对误差、平均相对误差,进而可以得出IPSO-ELM模型的平均预测精度为0.989 5,均方误差、平均绝对误差、平均相对误差分别为0.271 4、5.056 5%、0.260 3%。
表3 不同模型预测效果测试样本结果比较
Table 3 Prediction results comparison of different model
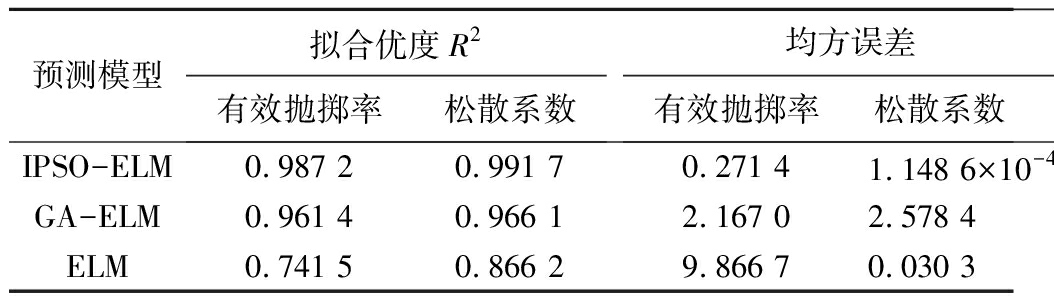
预测模型拟合优度R2有效抛掷率松散系数均方误差有效抛掷率松散系数 平均绝对误差有效抛掷率松散系数平均相对误差%有效抛掷率松散系数迭代次数IPSO-ELM0.987 20.991 70.271 41.148 6×10-40.571 3%0.004 40.159 70.360 940GA-ELM0.961 40.966 12.167 02.578 41.213 5%0.008 20.353 10.676 3100ELM0.741 50.866 29.866 70.030 36.239 6%0.135 217.251 811.317 6144
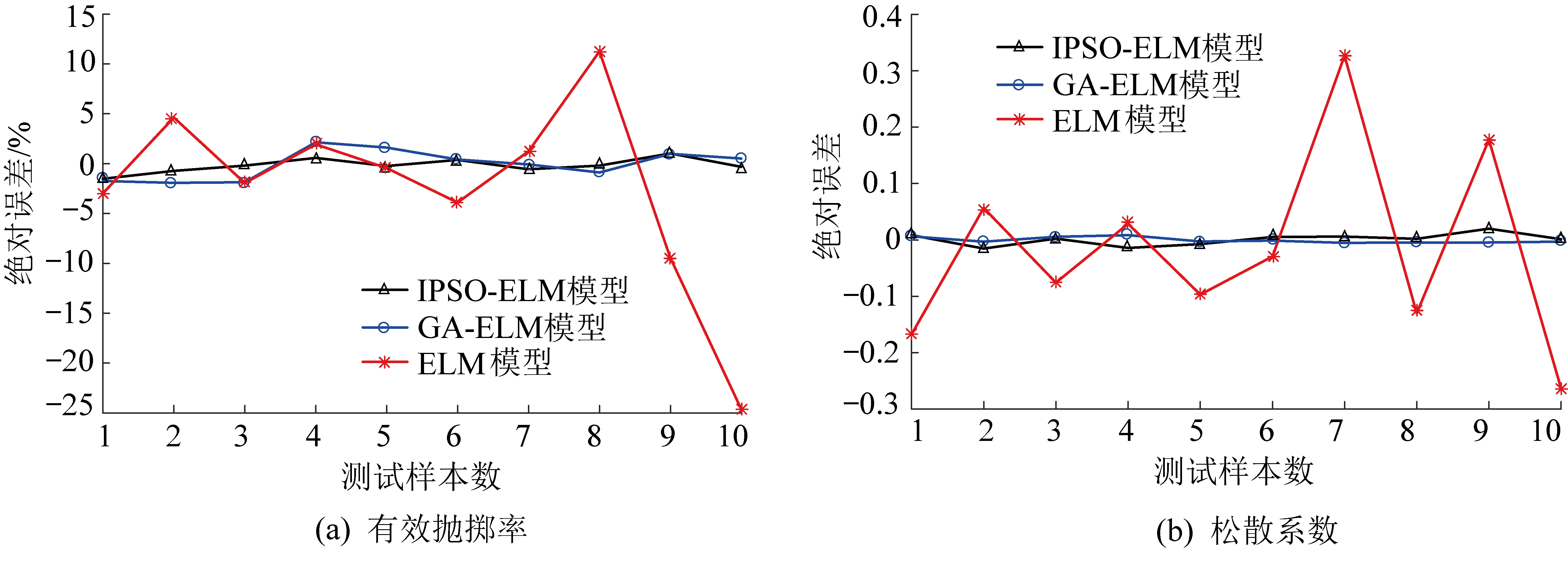
图6 绝对误差对比
Fig.6 Comparison of absolute errors
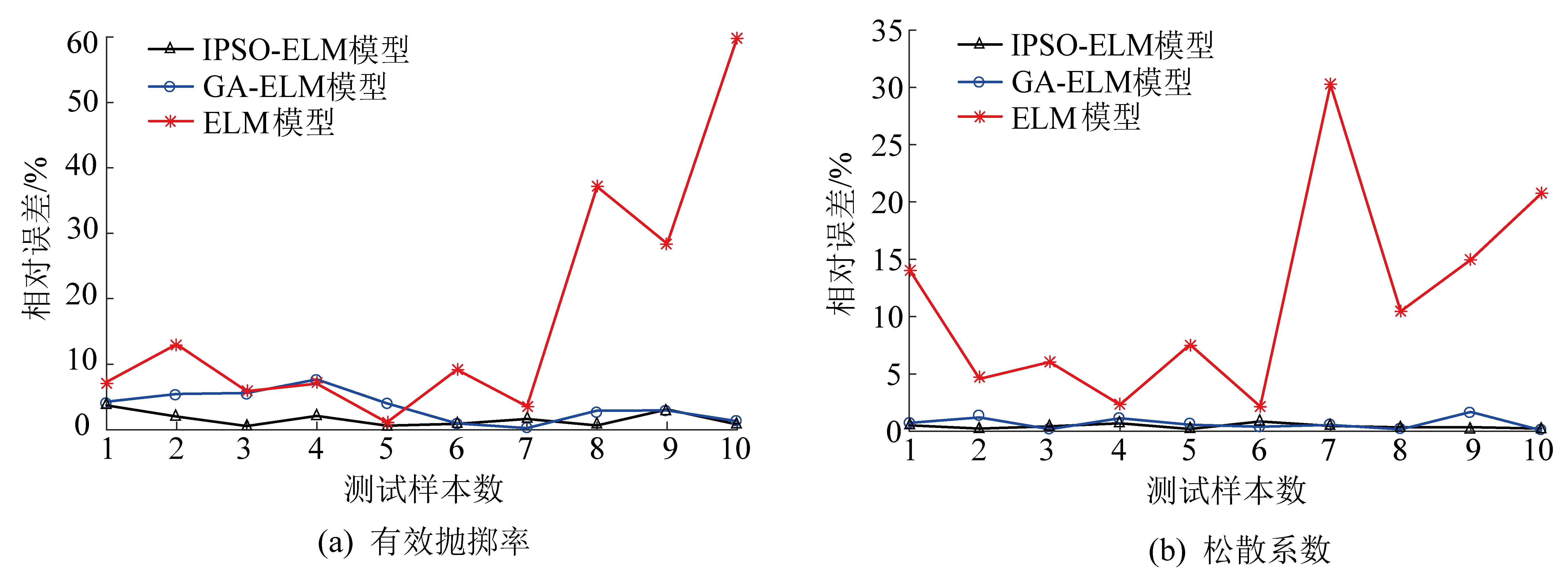
图7 相对误差对比
Fig.7 Comparison of relative errors
在迭代次数的对比中,IPSO-ELM模型的收敛速度明显较快。对比分析表明,与遗传算法相比,粒子群算法优化神经网络能够有效降低预测结果的误差,提高预测模型的泛化能力和预测效果。
4 结 论
1)选取炸药单耗、台阶高度、孔距、排距、最小抵抗线5个因素作为输入变量,有效抛掷率、松散系数作为输出变量,建立参数优化后粒子群算法和极限学习机相结合的露天矿抛掷爆破效果IPSO-ELM预测模型。
2)将常规粒子群算法中惯性权值和学习因子进行自适应和动态调整改进后,模型的迭代次数和运行时间缩短,收敛速度明显提高,改善了之前神经网络模型易于陷入局部最小值收敛速度慢的缺点。
3)IPSO-ELM模型平均预测精度达到0.989 5,均方误差、平均绝对误差、平均相对误差控制在0.271 4、5.056 5%、0.260 3%,且与ELM、GA-ELM智能算法相比,预测精度最高、预测误差最小,表明IPSO-ELM模型对于预测露天矿抛掷爆破效果具有较好的适用性。
[1] 傅洪贤,李克民.露天煤矿高台阶抛掷爆破参数分析[J].煤炭学报,2006,31(4):442-445.
FU Hongxian,LI Kemin.Analysis of high bench cast blasting parametersin surface coal mines[J].Journal of China Coal Society,2006,31(4):442-445.
[2] 李祥龙.高台阶抛掷爆破技术与效果预测模型研[D].北京:中国矿业大学(北京),2010:14-16.
[3] 刘 干,李克民,肖双双,等.露天煤矿抛掷爆破有效抛掷率预测[J].金属矿山,2014,43(4):65-69.
LIU Gan,LI Kemin,XIAO Shuangshuang,et al.Prediction of effective stripping ratio of casting blast in surface coal mines[J].Metal Mine,2014,43(4):65-69.
[4] 孙文彬,刘希亮,谭正龙.基于抛掷爆破预测BP神经网络参数优化方法[J].煤炭学报,2012,37(1):59-64.
SUN Wenbin,LIU Xiliang,TAN Zhenglong,et al.Parameter optimization of BP neural network based on the forecast of cast blasting[J].Journal of China Coal Society,2012,37(1):59-64.
[5] 刘希亮.基于GA-BP神经网络抛掷爆破效果预测与分析[D].北京:中国矿业大学(北京),2011.
[6] 温廷新,陈晓宇,邵良杉,等.参数优化GA-ELM模型在露天煤矿抛掷爆破的预测[J].煤炭学报,2017,42(3):630-638.
WEN Tingxin,CHEN Xiaoyu,SHAO Liangshan,et al.Prediction on parameters optimized GA-ELM model for cast blasting in open-pit mine[J].Journal of China Coal Society,2017,42(3):630-638.
[7] 王东风,孟 丽.粒子群优化算法的性能分析和参数选择[J].自动化学报,2016,42(10):1552-1561.
WANG Dongfeng,MENG Li.Performance analysis and parameter selection of particle swarm optimization algorithm[J].Acta Automatica Sinica,2016,42(10):1552-1561.
[8] 马 力,吕 粲,李克民,等.基于产量目标的露天煤矿倒堆台阶高度优化研究[J].中国煤炭,2014,40(3):56-59.
MA Li,LYU Can,LI Kemin,et al.Optimization research of stripping bench height of open-pit for its output target[J].China Coal,2014,40(3):56-59.
[9] 李祥龙,刘殿书,何丽华,等.露天煤矿的台阶高度对抛掷率的影响[J].爆炸与冲击,2012,32(2):211-215.
LI Xianglong,LIU Dianshu,HE Lihua,et al.Influences of bench height of an open-pit coal mine on cast percentage[J].Explosion and Shock Waves,2012,32(2):211-215.
[10] 马 力,李克民,丁小华,等.抛掷爆破岩体抛掷距离影响因素研究[J].工程爆破,2013(S1):50-53.
MA Li,LI Kemin,DING Xiaohua,et al.Study on the influencing factors on casting distance of rock by casting blast[J].Engineering Blasting,2013(S1):50-53.
[11] 马 力.近水平露天煤矿抛掷爆破条件下多煤层开采关键技术研究[D].徐州:中国矿业大学,2015.
[12] 郑炳旭,高荫桐,肖文雄,等.定向爆破抛掷距离研究与分析[J].爆破,2006,23(4):1-3.
ZHENG Bingxu,GAO Yintong,XIAO Wenxiong,et al.Research and analysis on casting distance of directional blasting[J].Blasting,2006,23(4):1-3.
[13] 马 力,李克民,常治国,等.基于抛掷爆破-拉斗铲倒堆工艺的露天矿生产能力研究[J].煤炭工程,2016,48(10):11-14.
MA Li,LI Kemin,CHANG Zhiguo,et al.Study on surface mine capacity with casting blast-dragline stripping technology[J].Coal Engineering,2016,48(10):11-14.
[14] 邵 晴.粒子群算法研究及其工程应用案例[D].长春:吉林大学,2017.
[15] 黄 利,杜伟伟,丁立新.基于Sigmoid惯性权重自适应调整的粒子群优化算法[J].计算机应用研究,2012,29(1):32-34.
HUANG Li,DU Weiwei,DING Lixin.Particle swarm optimization algorithm based on adaptive Sigmoid inertia weight[J].Application Research of Computer,2012,29(1):32-34.
[16] 殷 豪,董 朕,孟安波.基于结合混沌纵横交叉的粒子群算法优化极限学习机的短期负荷预测[J].计算机应用研究,2018,35(7):2088-2091.
YIN Hao,DONG Wei,MENG Anbo.Optimizing the short-term load forecasting of extreme learning machine based on particle swarm optimization based on chaotic vertical and horizontal crossover[J].Journal of Computer Applications,2018,35(7):2088-2091.
[17] LAN Yuan,Soh Y C,HUANG Guangbin.Ensemble of online sequential extreme learning machine[J].Neuro-computing,2009,72(13):3391-3395.
[18] HUANG Guangbin,DING Xiaojian,ZHOU Hongming.Optimization method based extreme learning machine for classification[J].Neuro-Computing,2010,74(1/3):155-163.
[19] 张志会.基于混沌优化极限学习机的库岸边坡变形预测[J].水力发电,2018,44(12):42-45,107.
ZHANG Zhihui.Prediction of bank slope deformation based on chaos optimization extreme learning machine model[J].Water Power,2018,44(12):42-45,107.
