0 引 言
地下开采引起的地表沉陷变形是一个极其复杂的随时间和空间变化的四维问题[1-4]。在不同的开采时间阶段沉陷灾害对地表工程建设产生的影响程度具有很大差异,因此,研究开采沉陷的动态过程对于沉陷灾害的预防和控制具有重要的理论意义和工程应用价值[5],是当前开采沉陷领域研究需要重点解决的问题之一。
目前采空区地表动态沉降预测时间函数模型有Knothe模型[6]、改进Knothe模型[7-8]、Logistic模型[9]、Gomepertz模型、Sroka-Schober模型[10]、Richards模型[11]和Weibull模型[12]等。上述模型在实际应用中取得了一定成果,但仍然存在一定程度的不足。研究表明,Knothe模型不符合地表沉降的客观过程[13];对此,常占强等[7]在2个反对称阶段沉降过程的基础上改进了Knothe模型,但改进后Knothe模型与Logistic模型、Gomepertz模型在拐点处的沉降量均是固定的[11],前两者等于最大沉降值的1/2,后者等于最大值的1/e,这并不完全符合实际沉降变形趋势变化规律。Sroka-Schober模型和Richards模型难以获得准确的参数[14-15]。Weibull模型中仅有2个参数,物理意义尚不明确,且存在临界沉降时刻难以确定问题,限制了该模型的应用[16]。MMF模型需要给出曲线拐点后的部分实测数据,实测数据的个数对预测精度的影响很大,其结果一般偏大[17]。针对上述存在的问题,笔者将描述信息增长预测的Usher函数[18]引入沉降预测中,研究表明,Usher模型能够较好地模拟采空区地表动态沉降过程,对于实际情况具有更广的适用范围和良好的预测精度。
1 采空区地表沉降规律分析
煤层开采引起的地表沉陷是一个随采场上覆岩层移动而逐渐发展且有限增长的过程。从实测资料来看,地表沉降与时间的关系曲线在形态上大致呈现为S型。地表沉降的演化过程大致可分为初始沉降、剧烈沉降和衰退沉降3个阶段,如图1所示。
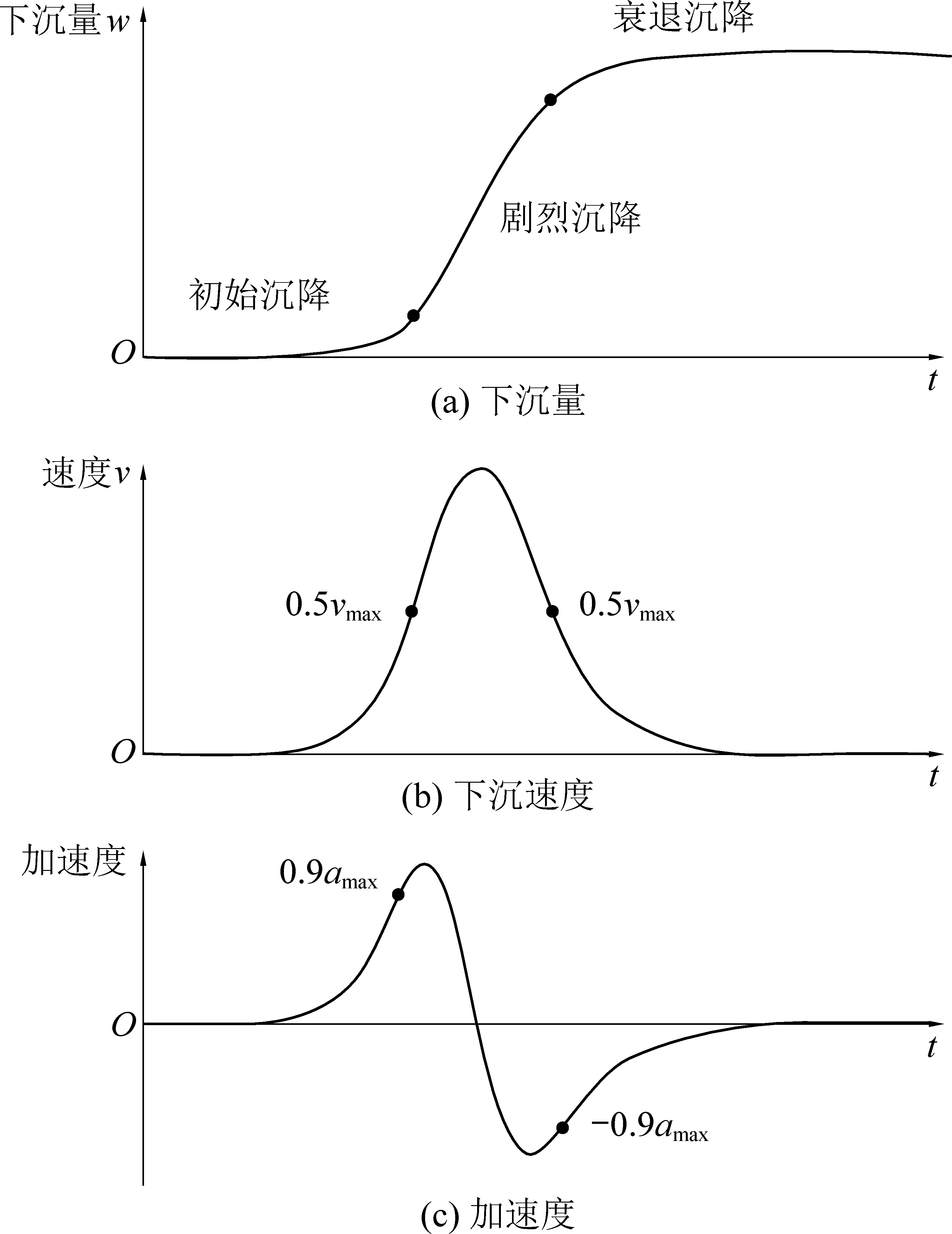
图1 采空区地表沉降动态发展过程
Fig.1 Dynamic development process of ground surface subsidence in goaf
1)初始沉降阶段,随着工作面推进,地表某点刚好被波及时,t=0,该点的沉降量w(t)、沉降速度v(t)和沉降加速度a(t)均为0。随采煤工作面的继续推进与时间的增加,v(t)从0开始缓慢增长接近至0.5vmax,a(t)从0增加接近至0.9amax。此阶段沉降量比较小,是地表随采空区顶板及上覆岩体发生垮落、断裂、弯曲而开始逐步发展的过程。
2)剧烈沉降阶段,w(t)随时间快速增大,a(t)由0.9amax增大最大值后减小负增长至-0.9amax,v(t)随时间增大至极限值后有所降低,基本大于0.5vmax。此阶段是地表随开采范围的增加达到充分采动,沉陷盆地范围扩大到最大的过程。
3)衰减沉降阶段,v(t)逐渐减小至0,a(t)由-0.9amax逐渐减小至0,w(t)继续缓慢增加并达到沉降极限值wmax。此阶段是采动离层裂隙闭合及垮落破碎岩体自然逐步压实的过程,一般持续时间较长。
描述地表沉陷动态过程的时间函数模型应满足2个方面的内容。首先,预测模型可以较好地拟合地表沉陷时间关系;其次,其沉降速度和加速度应符合地表沉陷的物理过程[19]。由于地表点的临界下沉时刻难以精确判断,在实际工程中通常按照文献[20]以沉降量达到10 mm的时刻作为下沉开始时刻[11],此时沉降速度和加速度均不为0。由此,描述地表沉降动态过程的理想模型应具备以下特征:①初始时刻:w(0)≠0,v(0)≠0,a(0)≠0。②时间从0→∞时,沉降量w(0)→wmax,沉降速度v(0)→vmax→0,沉降加速度a(0)→amax→0→amin→0。③沉降过程曲线应呈前端小后端大单调增长的“S”形状,速度曲线应具有为非对称性和拖尾特性,加速度曲线应呈现类正弦函数形状。
2 地表单点动态沉降预测的Usher模型
2.1 模型建立与通用性
Usher模型是美国学者Usher于1980年提出的用来描述增长信息随时间变化的数学模型[18],用于采空区地表动态沉降预测,其表达式为
(1)
式中:w为t时刻沉降量,mm;wm为极限沉降量,mm;b为曲线形状参数;a、c为沉降参数;t为时间,d。对式(1)的一阶、二阶导数可得地表沉降速度v(t)和加速度a(t)函数为
(2)
(3)
对Usher模型分析可知,若令b=1,该模型可简化为Logistic预测模型;若令b=-1,c=-1,该模型可简化为Knothe预测模型;若令b=-1,c=-c,该模型可得到为Mitscherlich Brody预测模型;若令b=-3,c=-c,该模型可得到为Von Bertalanffy预测模型;若令b→∞时,由(1)式经罗必塔法则求导并对其积分可得到Gompertz预测模型。由此可见,Logistic模型、Gompertz模型、Knothe模型、Mitscherlich Brody模型、Von Bertalanffy模型均是Usher模型的几种特例。Usher模型不仅具有更加广泛的普遍适应性,可以替代上述模型,而且可以准确描述中间的过渡类型,如图2所示。
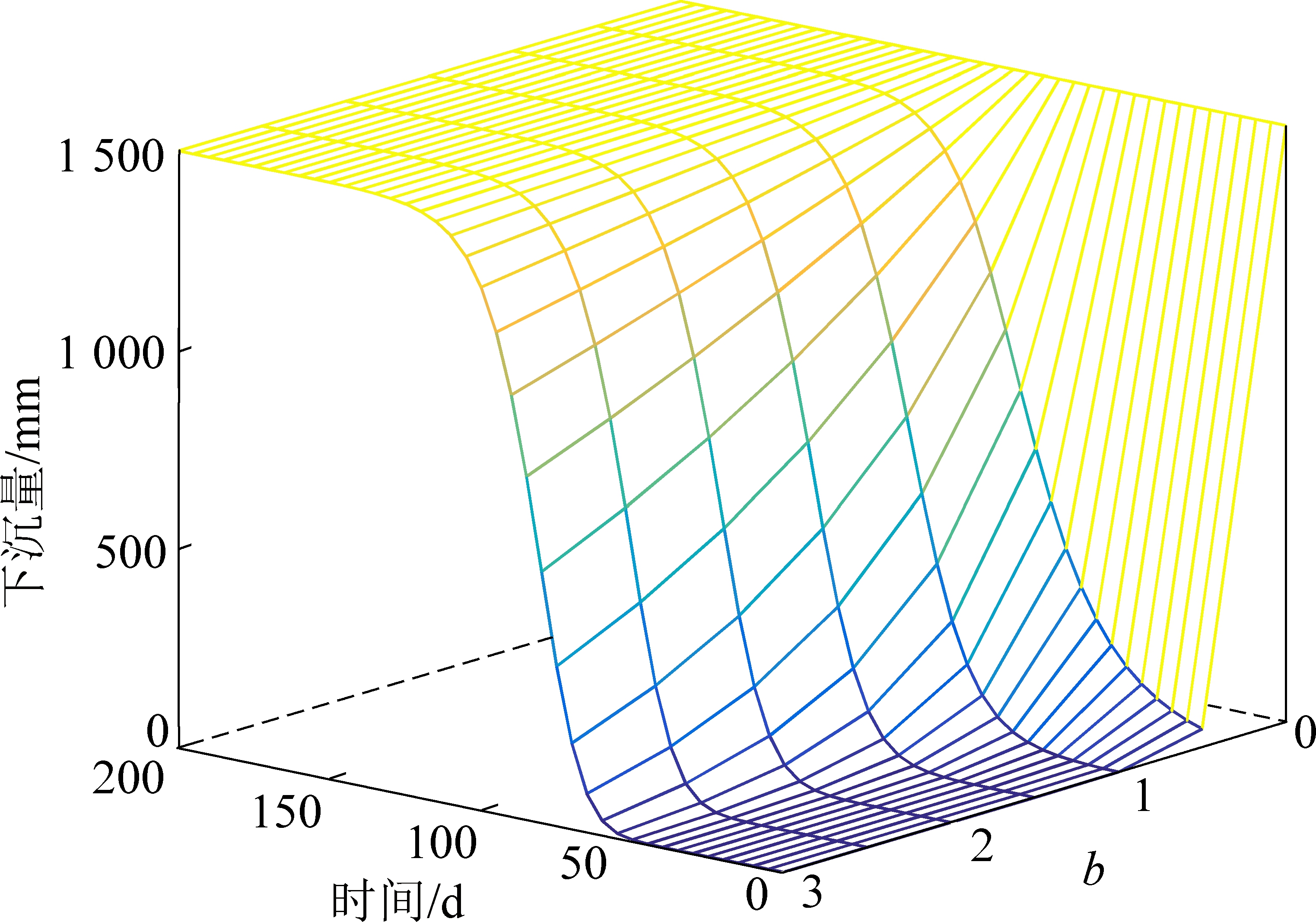
图2 Usher模型的通用性
Fig.2 Generalization of Usher model
定义模型函数的增长率为u,即
(4)
则可得到上述预测模型增长率的变化速度见表1。由表1可知,Logistic模型增长率的变化速度是与最终极限沉陷量有关的常数。Gompertz模型、Knothe模型、Mitscherlich Brody模型和Von Bertalanffy模型增长率的变化速度与瞬时沉降量w相关。Usher模型增长率的变化速度不仅与沉降量w有关,而且还取决于曲线的形状参数b[18],其值多变,并非一直下降。由此可见,Usher模型比其他模型具有更高的拟合精度和更强的适应性。
表1 模型表达式及增长率的变化速度
Table 1 Model expression and rate of change of growth rate

模型类型LogisticGompertzKnotheMitscherlich BrodyVonBertalanffyUsher函数表达式w=wm1+ce-atw=wme-cexp(-at)w=wm(1-e-at)w=wm(1-ce-at)w=wm(1-ce-at)3w=wm(1+ce-at)b模型增长率的变化速度dudwL=-awmdudwG=-awdudwK=-awmw2dudwM=-awmw2dudwV=-a3wmw4dudwU=-aw1b-1wm1b
2.2 模型参数分析
1)参数a对预测模型曲线的影响,参数wm反映了地表点的最终沉降量。取wm=1 500 mm,b=1.80,c=1 000,参数a的变化对模型曲线的影响如图3所示;由图3可知,参数a对沉降曲线、速度曲线和加速度曲线的影响明显。a越大,沉降曲线越陡,沉降速度和加速度变化越大,从开始沉降到达到稳定所需要的时间明显缩短,沉降速度和加速度的最大值均随a增加明显增大。

图3 参数a对地表沉降、沉降速度和沉降加速度的影响
Fig.3 Effect of parameter a on surface subsidence,subsidence velocity and subsidence acceleration
2)参数b对预测模型曲线的影响。取wm=1 500 mm,a=0.020,c=1 000,参数b的变化对模型曲线的影响如图4所示;由图4可以看出,参数b对沉降曲线、速度曲线和加速度曲线的影响明显。b越大,沉降曲线越陡,从开始沉降到达到稳定所需要的时间明显增长,沉降速度和加速度变化越大,沉降速度和加速度的最大值均随b增加明显增大。

图4 参数b对地表沉降、沉降速度和沉降加速度的影响
Fig.4 Effect of parameter b on surface subsidence,subsidence velocity and subsidence acceleration
3)参数c对预测模型曲线的影响。取wm=1 500 mm,a=0.02,b=1.80,参数c的变化对模型曲线的影响如图5所示。由图5可以看出,参数c对沉降曲线、沉降速度曲线和加速度曲线的形态影响不大,各曲线的平缓程度、总体变化趋势及最大值均保持不变。随着c增大,地表点沉降速度和加速度达到最大值的发生明显推迟,从开始沉降到达到稳定所需要的时间明显增加。

图5 参数c对地表沉降、沉降速度和沉降加速度的影响
Fig.5 Effect of parameter c on surface subsidence,subsidence velocity and subsidence acceleration
2.3 模型参数的确定
由式(1)可以看到,Usher模型是一个4参数的非线性方程,应用中需根据实测数据对Usher模型参数进行动态调整,以获得最佳的预测效果。设拟合已知有n组数据,(t1,w1)、(t2,w2)、…、(tn,wn),利用均方根误差公式进行求解,即
(5)
式中:wi为实测沉降值,![]() 为预测沉降值,mm。
为预测沉降值,mm。
式(5)求y最小值为最优。模型最优参数采用遗传算法(GA)进行求解,该方法是一种自适应全局优化概率搜索算法[20],在求解非线性函数方面有着很大优势[21]。基本思路是:将模型参数表示成“染色体”,进行随机初始化,依据优胜劣汰的原则,从中挑选出适应环境的“染色体”进行复制,通过交叉、变异形成新一代具有更强环境适应能力的染色体群,并以式(5)作为遗传算法的适应度函数,经过若干代的不断进化,从而得到问题的最优解。详细步骤参见文献[22]。
2.4 模型的适用性分析
受地层结构、开采深度、开采高度、开采方式及地层产状等种不同因素的影响,采矿引起的地表移动变形过程及破坏形式也表现出不同的类型。从模型所描述的沉降量、沉降速度及加速度来看,变化曲线为连续、可导的沉降过程。由此,Usher模型适合于地质采矿条件正常,深厚度较大,采动较为充分,覆岩三带显著发育采空区沉降预测。该模型不适合非充分采动条件下的非连续变形。
3 地表沉降的动态过程模型
根据文献[23],沉陷稳定后沉陷盆地走向或倾向主断面上的剖面数学函数为
(6)
式中:wm为沉陷盆地主断面上的最大下沉量,可采用文献[24]的经验公式估计;r为倾向方向沉陷影响半径,m;R为走向方向沉陷影响半径,m;k为沉降盆地形态参数。
而wm又有典型经验公式为
wm=mqcos α
(7)
式中:m为煤层厚度,mm;q为下沉系数;α为煤层倾角,(°)。
将Usher模型与沉陷盆地走向或倾向主断面上沉陷稳定后的剖面函数相结合,可建立整个沉陷盆地内任意点任意时刻的沉降量计算模型:
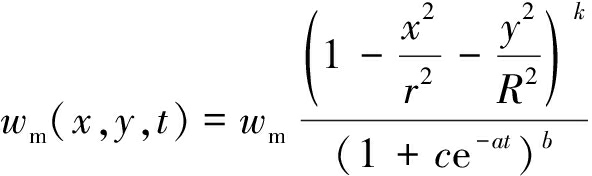
(8)
4 工程实例分析
以文献[25]所述的阳泉二矿8403综采工作面地表最大沉降63号点观测数据为例,对Usher时间函数模型进行验证其适用性,利用Matlab 2016a软件拟合了式(1)中的参数,wm=-3 233.4 mm,a=0.085 4,b=0.484,c=2 039 300,将拟合结果与实测沉降数据及其他模型预测数据进行对比,结果见表2、如图6所示。
表2 Usher模型与双参数Knothe模型及其他模型预测对比
Table 2 Prediction comparison of Usher model with two-parameter Knothe model and other models
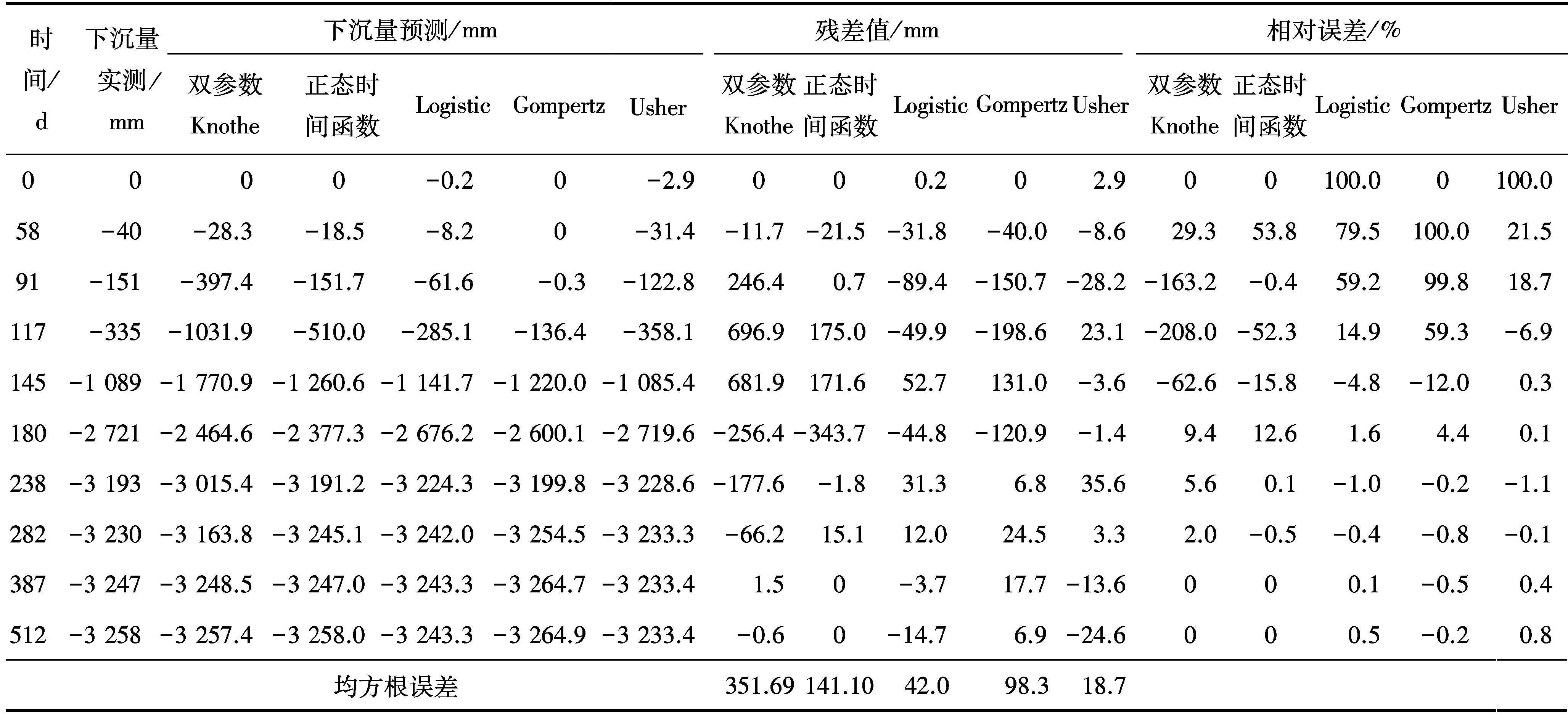
注:双参数Knothe预测数据和正态时间函数预测数据均来源于文献[25]。

图6 拟合结果与实测结果及其他模型预测结果对比
Fig.6 Comparison of fitting results with measured results and other model predictions
由表2和图6可知,笔者建立的Usher模型可以很好地反映地表单点下沉随时间的发展历程,拟合相关系数达到0.999,拟合结果良好。通过表2可知,采用Usher模型进行预计的均方根误差为18.7 mm,较文献[25]中双参数Knothe模型、正态时间函数模型及Logistic模型和Gompertz模型的预测均方根误差要小。由此可见,Usher模型预测的精度远高于其他预测模型。
用倾向主断面上的实测数据拟合,求出参数k=5.5,沉陷影响半径r=425 m,则倾向主断面动态预测公式为
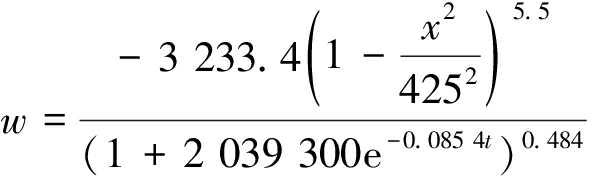
(9)
倾向主断面的下沉曲线随时间的变化过程如图7所示。

图7 倾斜主断面下沉曲线随时间变化
Fig.7 Change of the subsidence and time curve of incline section of the subsidence basin
5 结 论
1)在系统分析了采空区地表沉降3个阶段发展规律基础上,总结得出了采空区地表沉陷理想预测模型应具有能较好拟合地表沉降时间关系的沉降曲线,沉降速度和加速度应符合地表沉陷物理过程的基本特征。
2)针对采空区地表沉降预测模型存在的不足,提出了地表动态沉降预测的单点Usher模型,并将Usher模型与沉陷稳定后沉陷盆地走向或倾向主断面上的剖面函数相结合,构建了整个沉陷盆地内任意点、任意时刻的沉降量计算模型。通过对模型结构及其相关参数的深入分析,认为Logistic、Gompertz及Knothe等众多模型均是Usher模型的特例,Usher模型能够很好地反映采空区地表动态沉降过程,符合理想沉陷预测模型的基本要求。
3)根据Usher模型沉降量变化曲线为连续、可导的特性,Usher模型适合于地质采矿条件正常,深厚度较大,采动较为充分,覆岩三带显著发育采空区沉降预测。
4)工程实例证明,Usher时间函数模型比双参数Knothe模型、正态时间函数模型、Logistic和Gompertz等模型具有更强的适应性、更高的拟合精度和更好的预测效果,可准确预测采空区地表沉降量,可为开采沉陷预测提供一定的借鉴和参考。
[1] KNOTHE S.Proynozowanie wplywow eksploatacji girniczej[M].Wyd Slask Katowice:Katowice Polska,1984.
[2] 崔希民,缪协兴,赵英利,等.论地表移动过程的时间函数[J].煤炭学报,1999,24(5):453-456.
CUI Ximin,MIAO Xiexing,ZHAO Yingli,et al.Discussion on the time function of time dependent surface movement[J].Journal of China Coal Society,1999,24(5):453-456.
[3] 黄乐亭,王金庄.地表动态沉陷变形的3个阶段与变形速度的研究[J].煤炭学报,2006,31(4):420-424.
HUANG Leting,WANG Jinzhuang.Study on the three stages and deformation velocity of dynamic surface subsidence deformation[J].Journal of China Coal Society,2006,31(4):420-424.
[4] 谭志祥,邓喀中.建筑物下采煤理论与实践[M].徐州:中国矿业大学出版社,2009.
[5] 刘玉成.开采沉陷的动态过程及基于关键层理论的沉陷模型[D].重庆:重庆大学,2010.
[6] 胡青峰,崔希民,康新亮,等.Knothe时间函数参数影响分析及其求参模型研究[J].采矿与安全工程学报,2014,31(1):122-126.
HU Qingfeng,CUI Ximin,KANG Xinliang,et al.Impact of parameter on Knothe time function and its calculation model[J].Journal of Mining & Safety Engineering,2014,31(1):122-126.
[7] 常占强,王金庄.关于地表点沉降时间函数的研究——改进的克诺特时间函数[J].岩石力学与工程学报,2003,22(9):1496-1499.
CHANG Zhanqiang,WANG Jinzhuang.Study on time function of surface subsidence:the improved Knothe time function[J].Chinese Journal of Rock Mechanics and Engineering,2003,22(9):1496-1499.
[8] 王军保,刘新荣,刘小军.开采沉陷动态预测模型[J].煤炭学报,2015,40(3):516-521.
WANG Junbao,LIU Xinrong,LIU Xiaojun.Dynamic prediction model for mining subsidence[J].Journal of China Coal Society,2015,40(3):516-521.
[9] 徐洪钟,李雪红.基于Logistic增长模型的地表沉降时间函数[J].岩土力学,2005,26(S1):151-153.
XU Hongzhong,LIU Xuehong.Time function of surface subsidence based on logistic growth model[J].Rock and Soil Mechanics,2005,26(S1):151-153.
[10] KWINTA A,HEJMANOWSKI R,SROKA A.A time function analysis used for the prediction subsidence[C]//Proceeding of the Internation Symposium on Mining and Technology.Xuzhou:Balkema,1996:419-424.
[11] 王正帅,邓喀中.采动区地表动态沉降预测的Richards模型[J].岩土力学,2011,32(6):1664-1668.
WANG Zhengshuai,DENG Kazhong.Richards model of surface dynamic subsidence prediction in mining area[J].Rock and Soil Mechanics,2011,32(6):1664-1668.
[12] 刘玉成.基于Weibull时间序列函数的动态沉陷曲线模型[J].岩土力学,2013,34(8):2409-2413.
LIU Yucheng.Dynamic surface subsidence curve model based on Weibull time function[J].Rock and Soil Mechanics,2013,34(8):2409-2413.
[13] CUI Ximin.Prediction of progressive surface subsidence above longwall coal mining using a time function[J].International Journal of Rock Mechanics & Mining Sciences,2001,38(7):1057-1063.
[14] 彭小沾,崔希民,臧永强,等.时间函数与地表动态移动变形规律[J].北京科技大学学报,2004,26(4):341-344.
PENG Xiaozhan,CUI Ximin,ZANG Yongqiang,et al.Time function and prediction of progressive surface movements and deformations[J].Journal of University of Science and Technology Beijing,2004,26(4):341-344.
[15] 牛亚超.基于变步长FOA-Richards模型的地表沉降动态预计[J].黑龙江工程学院学报,2019,33(4):17-19,45.
NIUYachao.Dynamic prediction of surface subsidence based on variable step size FOA-Richards model[J].Journal of Heilongjiang Institute of Technology,2019,33(4):17-19,45.
[16] 朱广轶,沈红霞,王立国.地表动态移动变形预测函数研究[J].岩石力学与工程学报,2011,30(9):1889-1895.
ZHU Guangyi,SHEN Hongxia,WANG Liguo.Study of dynamic prediction function of surface movement and deformation[J].Chinese Journal of Rock Mechanics and Engineering,2011,30(9):1889-1895.
[17] 王军保,刘新荣,李 鹏,等.MMF模型在采空区地表沉降预测中的应用[J].煤炭学报,2012,37(3):411-415.
WANG Junbao,LIU Xinrong,LI Peng,et al.Study on prediction of surface subsidence in mined-out region with the MMF model[J].Journal of China Coal Society,2012,37(3):411-415.
[18] 赵明华,龙 照,邹新军.路基沉降预测的Usher模型应用研究[J].岩土力学,2008,29(11):2973-2976,2982.
ZHAO Minghua,LONG Zhao,ZOU Xinjun.Prediction of roadbed settlement by Usher model[J].Rock and Soil Mechanics,2008,29(11):2973-2976,2982.
[19] 刘玉成,曹树刚,刘延保.可描述地表沉陷动态过程的时间函数模型探讨[J].岩土力学,2010,31(3):925-931.
LIU Yucheng,CAO Shugang,LIU Yanbao.Discussion on some time function models for describing dynamic course of surface subsidence due to mining[J].Rock and Soil Mechanics,2010,31(3):925-931.
[20] 张文修,梁 怡.遗传算法的数学基础[M].西安:西安交通大学出版社,2000.
[21] 朱霄珣,徐搏超,焦宏超,等.遗传算法对SVR风速预测模型的多参数优化[J].电机与控制学报,2017,21(2):70-75.
ZHU Xiaoxun,XU Bochao,JIAO Hongchao,et al.Windspeed prediction method based on SVR and multi-parameter optimization of GA[J].Electric Machines and Control,2017,21(2):70-75.
[22] 余胜威.MATLAB优化算法案例分析与应用[M].北京 :清华大学出版社,2015.
[23] JOHNSON K L.Contact mechanics[M].Cambridge:Cambridge University Press,1985.
[24] 国家煤炭工业局.建筑物、水体、铁路及主要井巷煤柱留设与压煤开采规程[M].北京 :煤炭工业出版社,2000.
[25] 张 兵,崔希民,胡青峰.开采沉陷动态预计的正态分布时间函数模型研究[J].煤炭科学技术,2016,44(4):140-145,174.
ZHANG Bing,CUI Ximin,HU Qingfeng.Study on normal distributed time function model to dynamically predict mining subsidence[J].Coal Science and Technology,2016,44(4):140-145,174.
