0 引 言
煤矿地下开采引起的地表移动变形是一个复杂的时空过程[1-3]。地表沉陷不仅危及地面建筑、公路、铁路的安全,且容易诱发地质灾害,造成地表水的流失,从而对环境产生严重的破坏。为评估地表沉陷造成的危害,掌握地表沉陷的下沉量、范围、下沉速度、加速度等,地表沉陷的预测显得尤为重要[3-5]。对沉陷变形较为敏感的地面线性建筑如铁路、公路等而言,不仅受下沉量和下沉范围的大小控制,下沉速度和下沉加速度会对其产生更大的影响,所以静态预计已不能满足实践开采需求。为此,国内外学者展开大量地探索和研究,提出了不同的时间函数和地表动态沉陷预测理论[4]。
1952年,波兰学者Knothe利用土体压实的基本假设进行了地表移动和变形时间过程研究,提出了地表下沉速度与地表下沉量和时间的关系函数,即Knothe时间函数[6]。SROKA[7]和GONZALEZ-NICIEZA[8]基于Knothe时间函数分别提出了Sroka-Schober时间函数和正态分布时间函数。Knothe时间函数不能反映实际的下沉速度和下沉加速度变化规律[9-10],为了改进其不足,国内学者进行了大量的探索和研究,常占强等[11]提出了分段Knothe时间函数;张兵等[12]对分段Knothe时间函数进行了改进,拓宽了适用范围且提高了预计精度;王军保等[13]结合岩石流变力学中非定常流变模型,将时间影响系数看作与时间有关的变量,对Knothe时间函数进行了改进;文献[4,14]对正态分布时间函数进行了研究;刘玉成等[5,15]结合Weibull曲线模型对Knothe时间函数进行了改进,提出了Weibull时间函数模型,但参数物理意义还尚未明确。上述科研成果为地表沉陷预计研究以及实践运用起到了积极推动作用,为准确预测工作面采动引起的地面沉陷对铁路的影响,笔者以Weibull时间函数模型为基础,结合常村煤矿沉陷监测数据,分析模型参数的含义,提出了模型参数的变化曲线,并验证了其可靠性;同时证明了Weibull时间函数在常村煤矿动态预测中具有较高精度,能反映出实际的下沉过程,从而为常村煤矿后续工作面开采过程的动态预测提科学可靠的理论依据。
1 工程概况
常村煤矿位于山西省屯留县东部,郭庄煤矿铁路专用线从常村煤矿井田范围通过,据常村煤矿提供的相关资料显示,影响郭庄铁路专用线运营的回采工作面总共7个(图1),其中S3-13工作面已回采完毕。常村煤矿S3-13工作面从2016年8月开始回采,到2018年4月回采结束,平均采深487 m,煤厚5.82 m,煤层倾角1°~3°,工作面走向长度1 032 m,倾向长度228 m。上覆基岩主要为泥岩、砂岩以及砂质泥岩,该区属厚冲积层覆盖区,第四系表土层厚度为48.0~95.9 m,平均厚度达到78 m。采煤方法为综采放顶煤,全部垮落法管理顶板,工作面推进速度3.2 m/d。
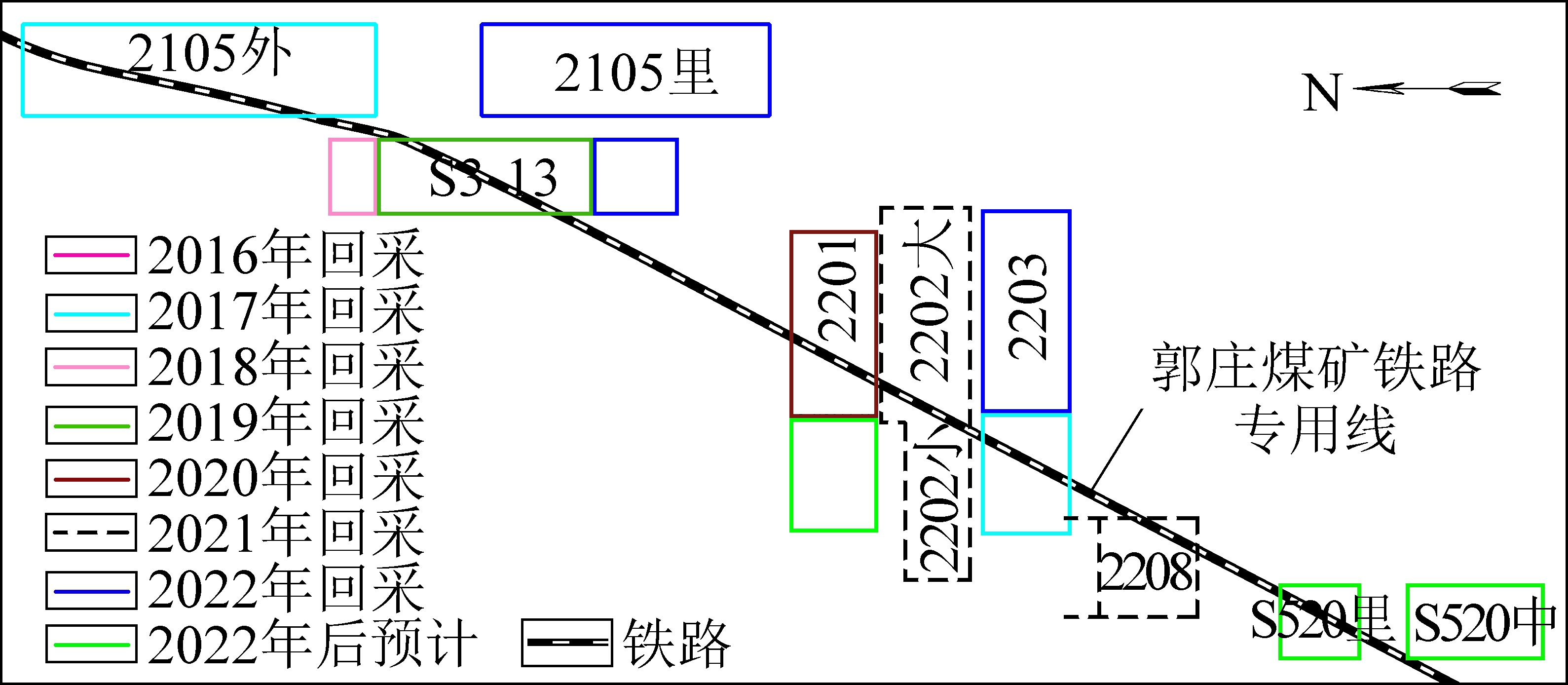
图1 工作面与铁路位置关系
Fig.1 Relation between working face and railway position
为掌握工作面开采对铁路的影响状况,郭庄煤矿在S3-13工作面布置了57个监测点,监测点布置如图2所示。2016年9月至2018年6月共进行了28次水准监测,水准测量按四等水准测量的精度要求进行。监测站设置和各监测工作均按《煤矿测量规程》及监测站设计说明书的要求进行,各项监测成果的精度符合规程要求,取得了真实可靠的监测数据。

图2 监测点布置
Fig.2 Monitoring site layout
2 Weibull时间函数模型
2.1 Weibull时间函数的完备性
引入Weibull曲线函数描述地表监测点动态沉陷过程,建立时间函数模型,其表达式为
W(t)=Wm[1-exp(-ctk)]
(1)
式中:Wm为监测点的最大下沉量,mm;t为监测点下沉时间,a;c、k均为与采空区上覆岩层性质有关的参数,k>1。
由式(1)推导出下沉速度v和下沉加速度a的计算分别为
v(t)=Wmcktk-1exp(-ctk)
(2)
a(t)=Wmckexp(-ctk)[(k-1)tk-2-ckt2(k-1)]
(3)
式(1)—式(3)的曲线特征如图3所示。
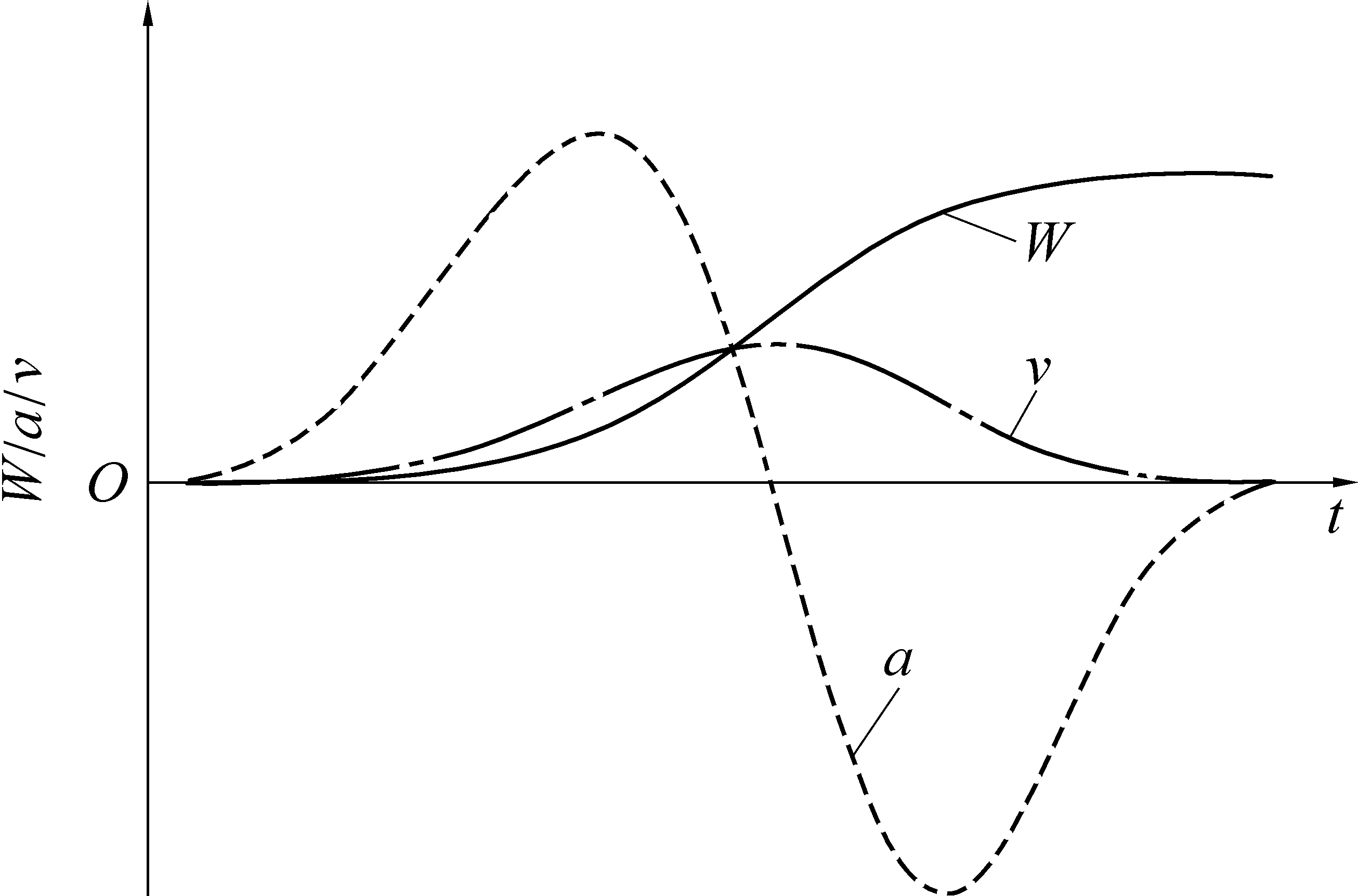
图3 Weibull时间函数、下沉速度、下沉加速度曲线特征
Fig.3 Weibull time function,subsidence velocity,subsidence acceleration curve characteristics
从图3可以看出:下沉量的变化过程为:0→Wm;下沉速度的变化过程为:0→vmax→0;下沉加速度的变化过程为:0→amax→0→amin→0;三者的变化曲线均与实际地表沉陷过程特征相一致,因此Weibull时间函数在时间和空间上具有很好的完备性。
2.2 模型参数的讨论
文献[16-17]认为参数c决定地表监测点从开始下沉到稳定的时间长短,而参数k决定监测点在时间轴上的运动路径。在有大量监测数据的基础上可采用最小二乘法确定这2个参数,而参数的理论计算方法还需进一步研究。为进一步了解模型参数c、k的物理意义,令
φ(t)=1-exp(-ctk)
(4)
式(4)为时间影响函数,则式(1)可表示为
W(t)=Wmφ(t)
(5)
对时间影响函数φ(t)进行分析,如图4所示。由图4a可知,当参数k取值相同时,下沉起始时间几乎一致,而下沉到达最大值的时间则受c的影响,c越小,所需时间越长,表明c控制整个下沉过程的时间长短(下沉持续时间);根据量纲分析可得出c的量纲为1/a或1/d,与下沉时间有关。从曲线斜率来看,下沉速度也随参数c的增大而增大。
由图4b可知,当参数c取值相同,k取不同值时,下沉起始时间变化较大,随着k取值增大,下沉起始时间也随之增大;而k取值不同对下沉达到稳定的时间影响不大;同时k越大曲线越陡,斜率越大,也即最大下沉速度越大。相较于c来说,k增大时,下沉持续时间缩短更快,也即是k对下沉持续时间的控制更强。
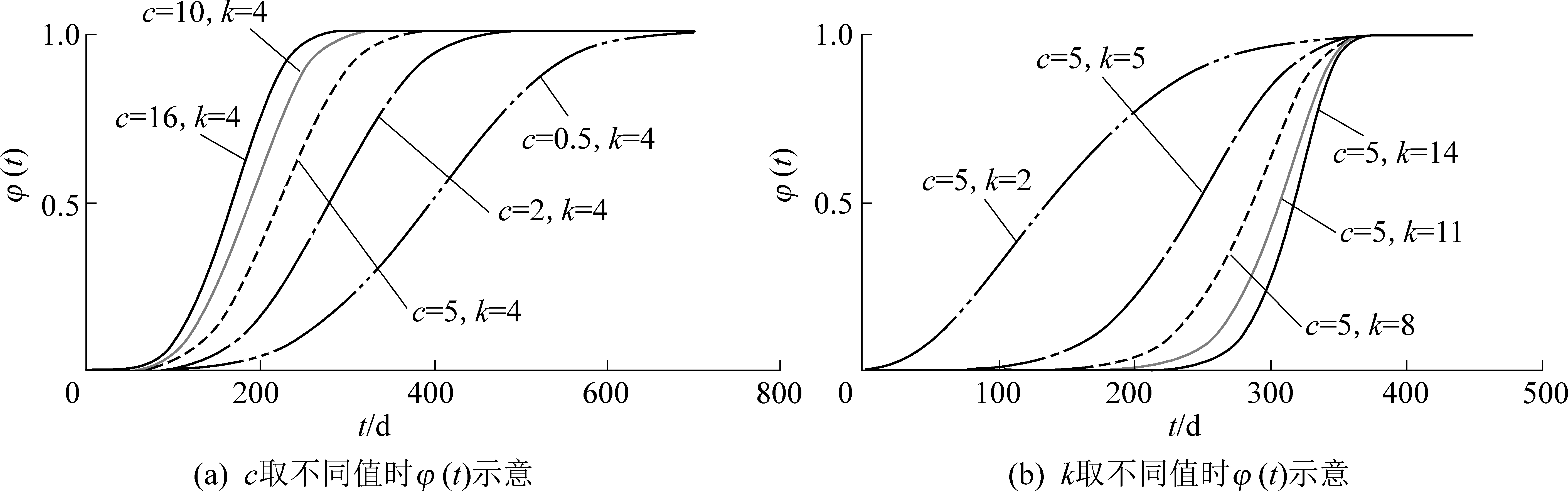
图4 参数c、k取值不同时φ(t)示意
Fig.4 Schematic diagram φ(t)of different values of parameter c and k
下文将对实测数据进行处理分析,深入解析参数c、k对沉陷过程的影响。
3 基于实测数据的模型参数分析
3.1 基于实测数据的模型参数简析
选取6个监测点数据,对下沉时间与下沉量之间的关系进行分析,如图5所示,可以看出监测点的下沉过程完全符合Weibull时间函数变化特征,Weibull时间函数可用来对常村煤矿进行开采沉陷的预测。
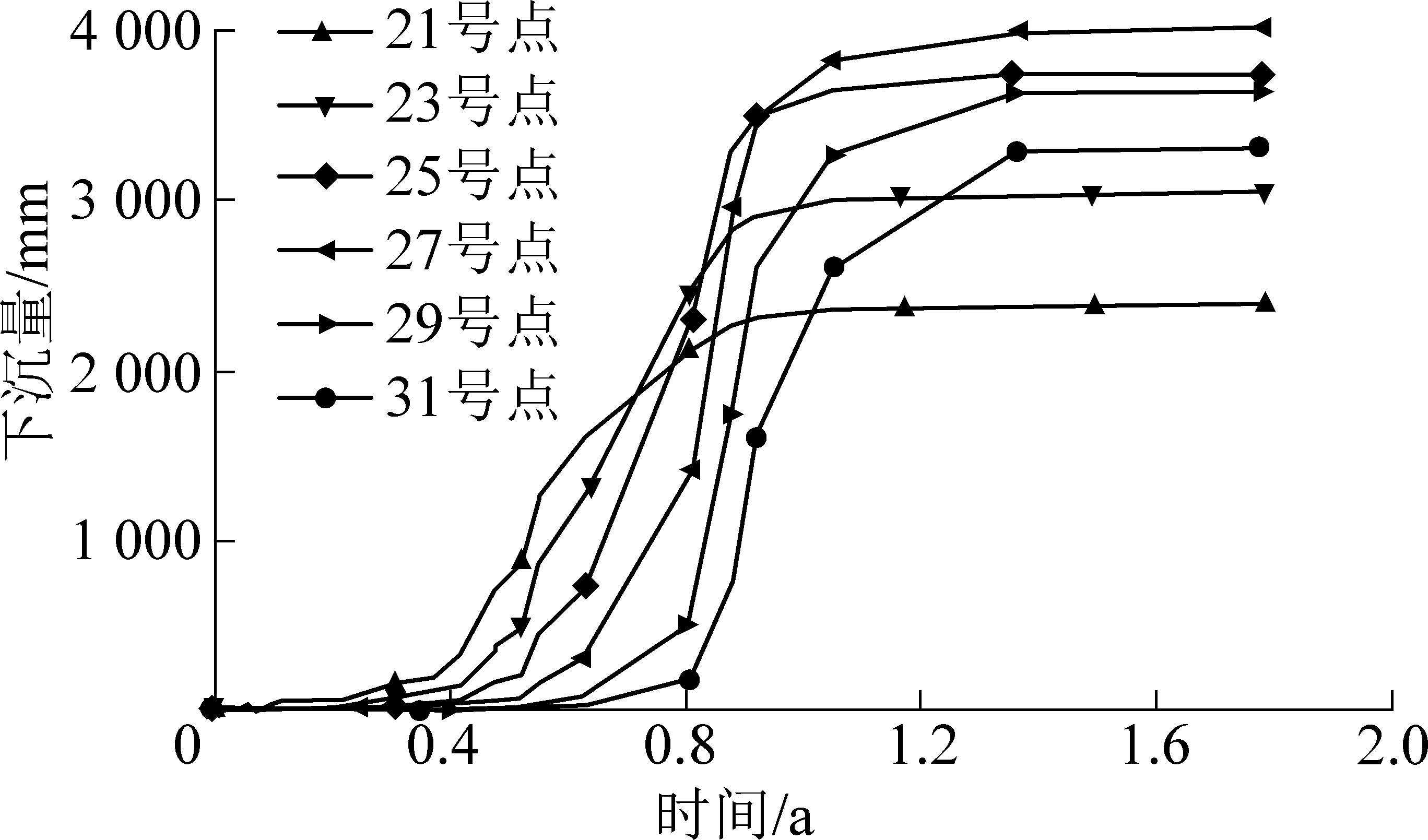
图5 下沉时间与下沉量关系曲线
Fig.5 Relation curves of sinking time and subsidence
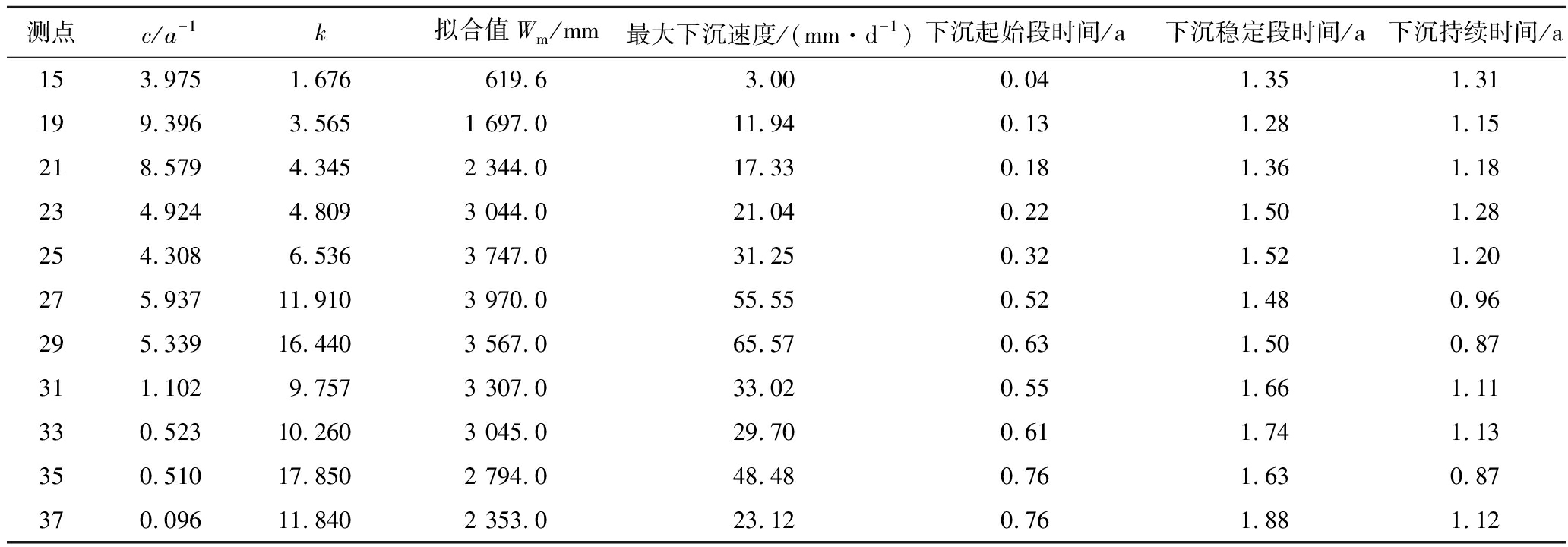
为进一步了解模型参数c和k的物理意义,选取11个监测点的监测数据,用式(1)进行拟合求参,结果见表1。依据《建筑物、水体、铁路及主要井巷煤柱留设与压煤开采规范》[16]下沉量达到10 mm为下沉的起点;下沉达到稳定判断依据为连续6个月下沉不超过30 mm,下沉稳定时间为开始回采到监测点下沉结束时间;最大下沉速度按文献[5]中式(24)计算。
表1 监测点拟合数据
Table 1 Observation point fitting data
测点c/a-1k拟合值Wm/mm最大下沉速度/(mm·d-1)下沉起始段时间/a下沉稳定段时间/a下沉持续时间/a153.9751.676619.63.000.041.351.31199.3963.5651 697.011.940.131.281.15218.5794.3452 344.017.330.181.361.18234.9244.8093 044.021.040.221.501.28254.3086.5363 747.031.250.321.521.20275.93711.9103 970.055.550.521.480.96295.33916.4403 567.065.570.631.500.87311.1029.7573 307.033.020.551.661.11330.52310.2603 045.029.700.611.741.13350.51017.8502 794.048.480.761.630.87370.09611.8402 353.023.120.761.881.12
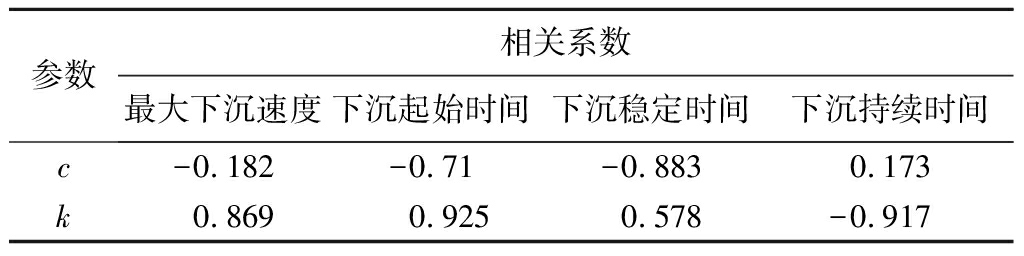
根据表1绘制参数c、k与最大下沉速度、下沉起始时间、下沉持续时间、下沉稳定时间的关系曲线,如图6所示;同时分别对参数c、k和最大下沉速度、下沉起始时间、下沉持续时间、下沉稳定时间进行了相关性分析,求得的Pearson相关系数见表2。
表2 Pearson相关系数
Table 2 Pearson correlation coefficient
参数相关系数最大下沉速度下沉起始时间下沉稳定时间下沉持续时间c-0.182-0.71-0.8830.173k0.8690.9250.578-0.917
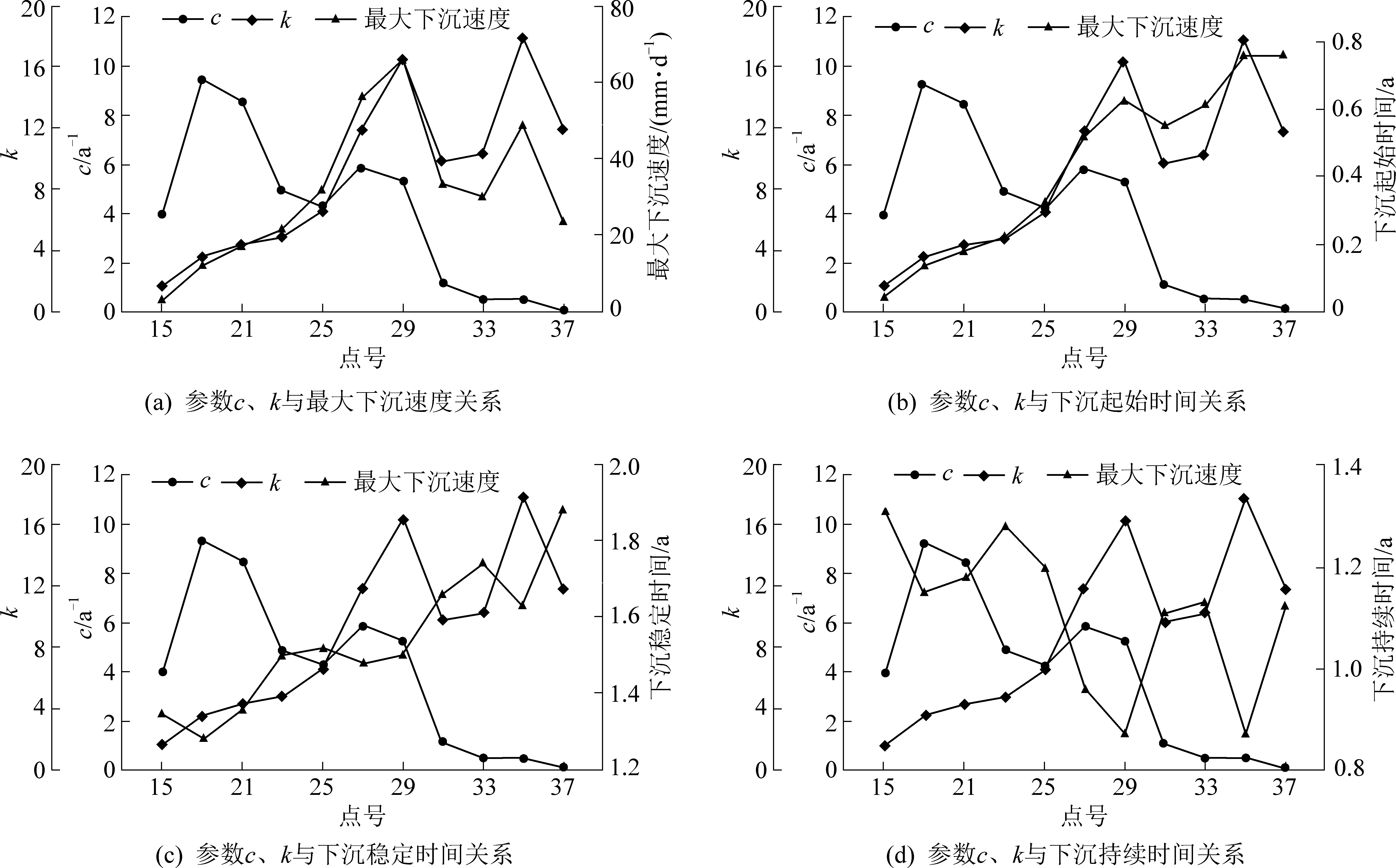
图6 参数c、k与各因素间的关系曲线
Fig.6 Relation curves of parameter c and k and each factor
结合图6a和表2,参数k与最大下沉速度变化规律一致,呈正相关,且相关度高;而参数c与最大下沉速度呈负相关,相关系数较小。表明参数k对最大下沉速度起主要影响作用。
结合图6b和表2,参数k与下沉起始时间变化规律一致,相关系数高达0.925,相关度极高;而参数c与下沉起始时间则呈负相关,相关度较高;表明下沉起始时间受参数c和k同时控制。图6b中35和37号监测点的下沉起始时间相同,但c和k数值均不同,在k值减小的同时,参数c也在减小,但是参数c减小的比例远大于k减小的比例,表明参数k的影响程度大于参数c的影响程度。下沉起始时间反映地表监测点离开切眼距离,往往距离越远,从开始回采到监测点开始下沉时间越长。
结合图6c和表2,参数c与下沉稳定时间呈负相关,相关度高;参数k与下沉稳定时间呈正相关,相关系数相对较小。图6c中25和27号监测点参数c的增大比例远小于参数k的增大比例,但是下沉稳定时间是减小的,表明参数c的影响程度大于参数k的影响程度。监测点的下沉稳定时间一方面受离开切眼的距离影响,另一方面受下沉速度制约。
结合图6d和表2,参数c与下沉持续时间呈正相关,相关性较小;参数k与下沉持续时间呈负相关,相关系数达到0.917,相关度极高。图6d中29和31号监测点参数c减小比例远大于参数k的减小比例,表明参数k的影响程度远大于参数c的影响程度。监测点的下沉持续时间越短表明下沉过程越剧烈,下沉速度越快。一方面与工作面的开采方式,顶板管理方法等有关,另一方面与上覆基岩的厚度和岩性、松散层的厚度等有关。
综上,参数c主要影响下沉起始时间及下沉稳定时间,且都呈负相关,但是参数c并不是决定地表监测点从开始下沉到稳定的时间长短(下沉持续时间)的关键参数,主要体现的是监测点距开切眼的位置、煤层埋深、上覆岩层的厚度及其性质等。参数k主要影响下沉起始时间、最大下沉速度、下沉持续时间,对下沉稳定时间的影响相对较小,反映了监测点下沉速度快慢和剧烈程度,说明参数k与监测点离开切眼的距离、工作面的开采方法和顶板管理方法、上覆基岩和松散层厚度及其性质等有关。
结合实测数据和上述图表,参数c、k的取值存在一定的变化规律,如图7所示。在沉陷边界外,将下沉量当做0处理。对于开切眼较近的沉陷边界,为确保Wm=0,φ(t)应恒等于0;经计算,参数k趋近于1,参数c趋近于0。对于终采线较近的沉陷边界,监测点的位置离开切眼位置越远,下沉速度越小,下沉达到稳定所需时间越长,参数k如果一直减小将不能保证下沉起始时间维持在较大值,为满足实际下沉规律,笔者认为参数k在接近沉陷边界处时,是趋近于某一定值k1(k1>1)的,为保证φ(t)恒等于0,参数c应逐渐趋近于0。下沉持续时间和下沉稳定时间都受下沉速度的影响,综合上述分析笔者认为参数k的最大值应在最大下沉速度位置。而对于参数c的最大值cmax所处位置,仍需要进一步研究,但是可以确定的是参数c的最大值位置较参数k离开切眼位置更近。
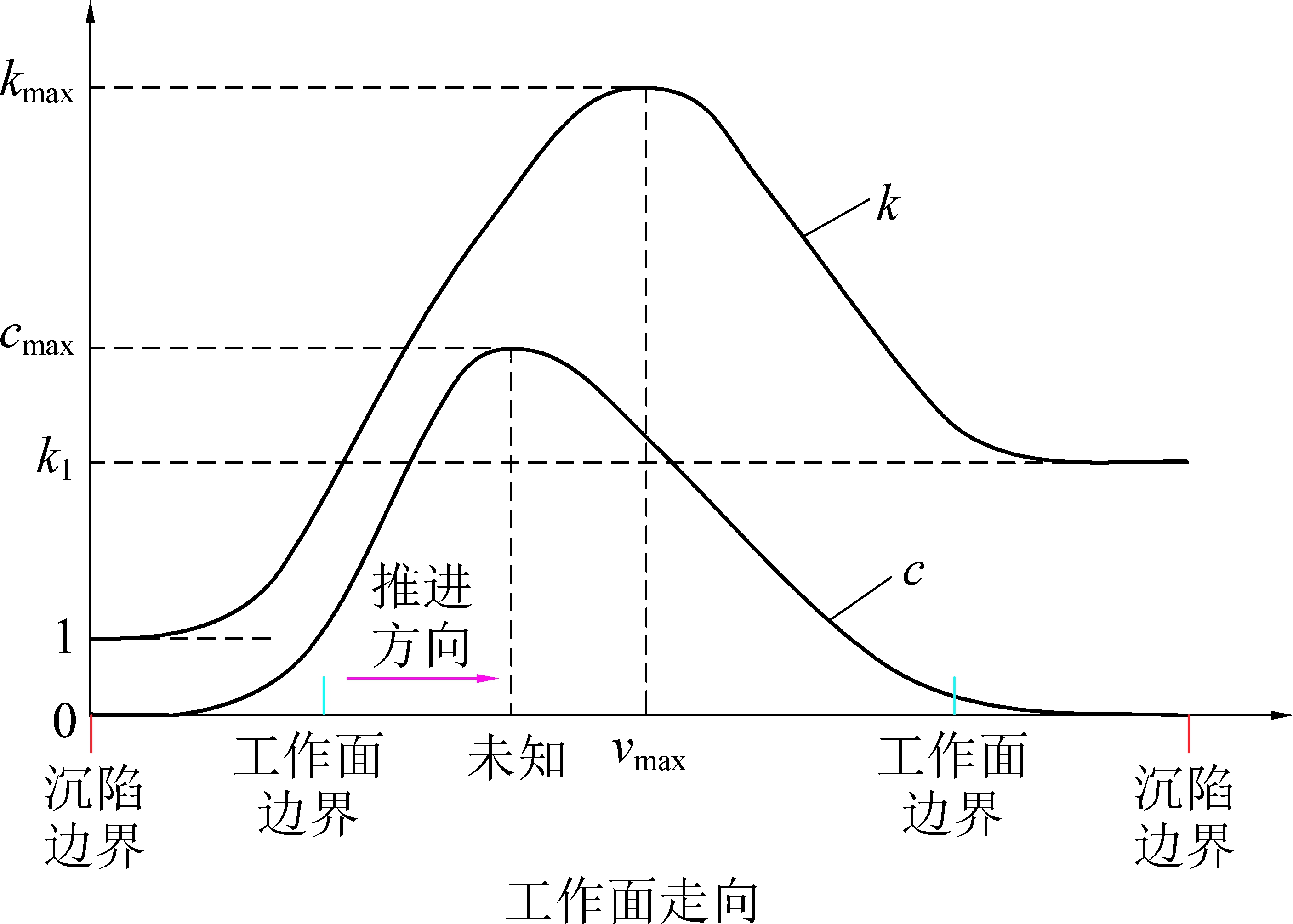
图7 参数c和参数k的变化规律示意
Fig.7 Schematic of variation rules of parameters c and k
目前,Weibull时间函数在实际运用中都是在基于大量监测数据的前提下,采用最大下沉值拟合求得的参数c、k进行地表动态沉陷预计。但是,对同一工作面来说,各监测点的下沉过程在时间和空间上是独立的[16],沉陷过程先后不一,同一时刻下沉速度、下沉量大小不一导致同一工作面不同监测点参数不一致,所以固定参数难以满足预计精度要求。在没有大量实测数据时,参数c可以按崔希民[9-10]给出的经验取值范围和计算公式确定或者参考周边及类似地质采矿条件矿区的参数c和k。
3.2 实测点验证
为验证图7的可靠性,选取7个监测点采用式(1)拟合求参,得到结果见表3;结合表1和表3,可以看出参数c、k均符合图7中的变化规律,表明图7是可靠的。从表3中选取2个点进行动态预测,如表4和图8所示。由实测数据计算可知,30号监测点处下沉速度最大,最大下沉速度为64.50 mm/d;而预计得到最大下沉速度为67.09 mm/d,同样位于30号监测点;表3中,拟合求参得到的R2都接近于1,拟合效果显著;表4中,2个监测点的相对误差分别为2.11%和2.66%。以上结论说明了Weibull时间函数对常村煤矿地表沉陷进行预测的精度高,误差小,可以很清楚地反映常村煤矿的动态沉陷过程。

图8 下沉实测值与预测值对比
Fig.8 Comparison of measured and predicted values of subsidence
表3 监测点拟合求参结果
Table 3 Evaluation results of observation point fitting
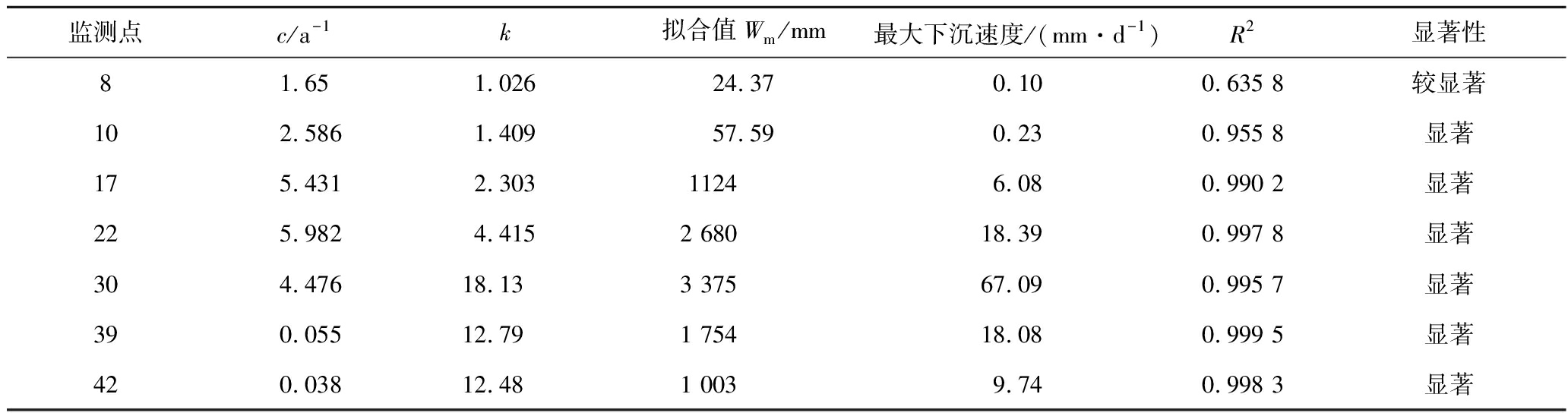
监测点c/a-1k拟合值Wm/mm最大下沉速度/(mm·d-1)R2显著性81.651.02624.370.100.635 8较显著102.5861.40957.590.230.955 8显著175.4312.30311246.080.990 2显著225.9824.4152 68018.390.997 8显著304.47618.133 37567.090.995 7显著390.05512.791 75418.080.999 5显著420.03812.481 0039.740.998 3显著
表4 下沉量实测值与预测值对比
Table 4 Comparison of measured and predicted values of subsidence

观测日期22号监测点下沉量/mm30号监测点下沉量/mm实测值预测值误差实测值预测值误差2016-09-04-3030002016-09-22-50530-32016-09-26-80830-32016-10-08-808130-132016-10-11-22-12190-92016-10-18-45-144-160162016-10-28-46-44240-42016-11-02-50-545-3032016-11-09-45-83730-32016-11-16-52-1339-2022016-11-24-49-202960-62016-12-27-107-90170002017-01-10-122-151-2920-22017-01-23-142-215-73-5052017-02-09-222-326-104-120122017-03-02-542-560-18-4042017-03-15-665-760-95-2022017-03-28-1 096-932164-7072017-04-26-1 509-1 44960-52-3492017-06-29-2 344-2 427-83-304-315-112017-07-26-2 566-2 591-25-1 211-1 20382017-08-10-2 607-2 637-30-2 114-2 117-32017-09-29-2 670-2 678-8-2 972-3 375-4032018-01-18-2 701-2 68021-3 460-3 375852018-04-08-2 706-2 68026-3 478-3 3751032018-05-23-2 705-2 68025-3 477-3 3751022018-06-22-2 707-2 68027-3 487-3 375112均方根误差/%——57.1——92.76相对误差——2.11——2.66
4 结 论
1)Weibull时间函数在下沉量、下沉速度、下沉加速度方面变化过程:0→Wm;下沉速度变化过程:0→vmax→0;下沉加速度变化过程:0→amax→0→amin→0;这与常村煤矿的地表下沉特征一致,表明该时间函数在时间和空间上具有完备性。
2)通过分析实测数据拟合得到的参数,确定了参数c不是决定下沉持续时间的关键因素,其主要影响下沉起始时间及下沉稳定时间,且都呈负相关;参数k主要影响下沉起始时间、最大下沉速度、下沉持续时间,对下沉稳定时间的影响相对较小,主要反映下沉速度快慢和剧烈程度,与监测点离开切眼位置、工作面的开采方法、上覆基岩和松散层厚度及其性质等有关。并提出了参数c和参数k的变化规律。
3)结合多个监测点的实测数据,验证了参数c、k变化曲线的可靠性;经过对下沉实测值和预测值对比分析,得到2个监测点的相对误差分别为2.11%和2.66%;说明Weibull时间函数在进行常村煤矿地表沉陷预测时,能得到较高精度的预测结果,反映出实际的下沉过程。
[1] 彭小沾,崔希民,臧永强,等.时间函数与地表动态移动变形规律[J].北京科技大学学报,2004,26(4):341-344.
PENG Xiaozhan,CUI Ximin,ZANG Yongqiang,et al.Such as a function of time and the dynamic movement and deformation of the surface[J].Journal of Beijing University of Science and Technology, 2004,26(4): 341-344.
[2] 张 兵,崔希民,胡青峰.开采沉陷动态预计的正态分布时间函数模型研究[J].煤炭科学技术,2016,44(4):140-145,174.
ZHANGBing,CUI Ximin,HU Qingfeng.Study the normal distribution model function of time of Mining Settlement Dynamic Estimation[J].Coal Science and Technology, 2016,44(4):140-145, 174.
[3] 李春意,陈 洁.岩移观测数据处理及曲面拟合参数求取研究[J].煤炭科学技术,2012,40(11):98-102.
LI Chongyi,CHEN Jie.Rock shift data processing and surface fitting parameters[J].Coal Science and Technology, 2012,40(11): 98-102.
[4] 李春意,高永格,崔希民.基于正态分布时间函数地表动态沉陷预测研究[J].岩土力学,2016,37(S1):108-116.
LI Chongyi,GAO Yongge,CUI Ximin.Normal time function based on the dynamic surface subsidence Prediction[J].Rock and Soil Mechanics,2016,37(S1):108-116.
[5] 刘玉成,曹树刚,刘延保.可描述地表沉陷动态过程的时间函数模型探讨[J].岩土力学,2010,31(3):925-931.
LIU Yucheng,CAO Shugang,LIU Yanbao.Discussion on some time functions for describing dynamic course of surface subsidence due to mining[J].Rock and Soil Mechanics,2010,31(3):925-931.
[6] KNOTHE S.Time influence on a formation of a subsidence surface[J].Archiwum Gómictwai Hutnictwa, Kraków(in Polish),1952,1(1):1.
[7] KWINTA A,HEJMANOWSKI R,SROKA A.A time function analysis used for the Prediction of rock mass subsidence[C]//Xuzhou: Proceeding of the International Symposium on Mining Science and Technology,1996:419.
[8] GONZALEZ NICIEZA C,ALVAREZ FERNANDEZ M I,MENENDEZ Diaz A,et al.The influence of time on subsidence in the Central Asturian Coalfield[J].Bulletin of Engineering Geology and the Environment, 2007, 66(3):319-329.
[9] CUI Ximin.Prediction of progressive surface subsidence above lon-gwall coal mining using a time function[J].International Journal of Rock Mechanics & Mining Sciences, 2001, 38(7):1057-1063.
[10] 崔希民, 缪协兴, 赵英利, 等.论地表移动过程的时间函数[J].煤炭学报, 1999, 24(5): 453-455.
CUI Ximin,MIAO Xiexing,ZHAO Yingli,et al.Discussion on the time function of time dependent surface movement[J].Coal Society, 1999, 24(5):453-455.
[11] 常占强,王金庄.关于地表点下沉时间函数的研究:改进的克诺特时间函[J].岩石力学与工程学报,2003,22(9):1496-1496.
CHANG Zhanqiang,WANG Jinzhuang.Research on surface subsidence points a function of time: improved Knothe a function of time[J].Journal of Rock Mechanics and Engineering, 2003,22(9): 1496-1496.
[12] 张 兵,崔希民.开采沉陷动态预计的分段 Knothe 时间函数模型优化[J].岩土力学,2017,38(2):541-548.
ZHANG Bing,CUI Ximin.Mining subsidence expected dynamic optimization model segment Knothe time function[J].Rock and Soil Mechanics, 2017,38(2): 541-548.
[13] 王军保,刘新荣,刘小军.开采沉陷动态预测模型[J].煤炭学报,2015,40(3):516-521.
WANG Junbao,LIU Xinrong,LIU Xiaojun.Dynamic prediction model for mining subsidence[J].Journal of China Coal Society, 2015,40(3):516-521.
[14] 张 凯,胡海峰,廉旭刚,等.地表动态沉陷预测正态时间函数模型优化研究[J].煤炭科学技术,2019,47(9):235-240.
ZHANG Kai,HU Haifeng,LIAN Xugang,et al. Optimization of surface dynamic subsidence prediction normal time function model[J].Coal Science and Technology,2019,47(9):235-240.
[15] 刘玉成.基于Weibull时间序列函数的动态沉陷曲线模型[J].岩土力学,2013,34(8):2409-2413.
LIU Yucheng.Dynamic surface subsidence curve model based on Weibull time function[J].Rock and Soil Mechanics,2013,34(8):2409-2413.
[16] 国家安全监管总局,国家煤矿安监局,国家能源局,等.建筑物、水体、铁路及主要井巷煤柱留设与压煤开采规范[M].北京:煤炭工业出版社,2017.
