0 引 言
地下开采引起地表下沉是一个随时间和空间变化的复杂过程[1-2],为确保采空区上方建(构)筑物的安全性,及时采取合理的预计和保护措施显得尤为重要。目前国内文献主要研究的开采沉陷动态预计模型主要包括:Knothe函数模型[2-5]、Weibull函数模型[6-8]、正态分布模型[9-10]等。
崔希民等[2]以Knothe函数为基础,探讨了时间影响系数c的确定方法,并给出了c的取值范围,建立了动态预计模型。胡青峰等[4]基于崔希民的模型进行改进,结合概率积分法对时间影响系数c进行推导。常占强等[3]通过分析Knothe函数表达地表下沉速度和加速度的缺陷以及地表下沉规律,提出将地表下沉过程一分为二的思想。以最大下沉速度出现的时间点(下沉总时间的1/2)为依据分为前后两部分,第1部分描述下沉速度由零增至最大,第2部分描述下沉速度由最大下降至零的过程,以原始Knothe函数的导数表示后半段,对称地表示出前半段即为下沉速度式,对其积分便为地表下沉动态预计式。张兵等[5]以常占强的理论为基础进行优化,解决了原时间函数在分段处函数值与理论值不一致以及原时间函数最终不收敛于1的问题。涂许航等[7]、王伟等[8]采用Weibull函数预计模型对矿区进行预计,解决了最大下沉速度对应的下沉值与最大下沉值比值为定值的问题。张兵等[10]研究了基于正态分布的动态预测模型。李春意等[9]讨论了正态分布的完备性。张凯等[11]对正态时间函数模型进行了优化。但笔者分析研究发现,地表下沉受开采速度、开采深度、地质条件等众多因素影响,其模型参数固定化,参数单一化会造成精度损失,从而可能引起下沉速度、下沉加速度表达与实际不符的问题。
一些学者应用不同的方法对工作面推进速度与地表下沉的关系进行了研究。谢广祥等[12]采用相似材料模拟法分析了不同推进速度对工作面上覆岩层的影响;王方方等[13]采用Knothe函数模型分析了不同推进速度下地表随时间变化的下沉规律。贾新果等[14]根据多个实测站实测数据,分析总结了工作面推进速度与地表移动的关系。宁永香等[15]分析了推进速度对地表建筑物的影响。
上述地表动态预计模型未很好解决参数单一化,固定化以及模型表达不完整的问题。鉴于此,笔者借鉴变异函数中高斯模型的建模思路,综合概率积分法求解出地表下沉时间,对比分析出普遍适用于地表下沉模型的参数,从而建立地表下沉动态预计模型。
1 变异函数模型的构造
1.1 坐标系的建立
建立半无限开采时间坐标系,如图1所示,坐标系分为地面坐标系和地下时间坐标系。地面坐标系原点x-o的位置为地下开切眼处向上垂直延伸至与地表的交点,回采方向为x轴的正方向,纵坐标表示下沉量,向下为正。地表坐标系用于表示地表观测点的位置。地下时间坐标系以开切眼为原点s-o,横坐标s与地上坐标系相对应,并将回采距离s用回采时间t表示,回采工作面推进速度vt,即t=s/vt。

图1 半无限开采时间坐标系
Fig.1 Coordinate system of time in semi-infinite mining process
1.2 地表下沉规律
采动过程中地表沉陷变形全过程分为3个阶段[16],即初始下沉阶段、活跃下沉阶段、衰减下沉阶段。其判断依据为地表点下沉速度:开采初期,当地表点下沉速度未达到1.67 mm/d时为初始下沉阶段;下沉速度大于1.67 mm/d时为活跃下沉阶段;下沉速度再次低于1.67 mm/d为衰减下沉阶段。地表点下沉曲线随时间变化呈“Z字”形,其下沉速度曲线近似于正态分布曲线,其变化趋势为0→vmax→0,下沉加速度的变化趋势为0→amax→0→amin→0。
1.3 函数模型构造
采用数字特征分析技术可以概括区域一些特征量的全貌,而变异函数则能反应局部范围和特定方向上的特征变化。由于变异函数能透过其随机性反应区域变化量的结构性,因此,变异函数也称为结构函数[17]。在半无限开采动态预计中,下沉时间函数可以表示为任一时间t,相距|Δt|的2个区域化变量值Z(t)及Z(t+Δt)的增量方差,表达式为
(1)
式中:γ(t,Δt)称为半变异函数,简称为变异函数;Ω为变量的作用域。
当Z(t)在动态预计中可表示为预计点t时刻的下沉量,Z(t+Δt)表示为预计点t+Δt时刻的下沉值。将式(1)拟合高斯理论模型,得到其通式为
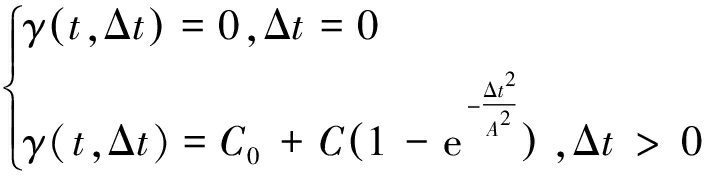
(2)
式(2)对应的曲线图像如图2所示,图中 C0称为金块效应,其表示当Δt很小时,在t和t+Δt时下沉量的变化;C称为总基台值,表示某区域化变量在研究范围内变异的强度[17],A为变程。

图2 高斯模型的变异函数曲线
Fig.2 Curve of variogram of gaussian model
根据下沉规律可知:初始开采的下沉量为0,而该曲线模型在Δt=0时并不符合下沉规律。因此将式(2)标准化:取C0=0,C=w0(w0为最大下沉量),则式(2)可表示为

(3)
式(3)的下沉曲线满足由开采引起的地表下沉规律,但下沉速度和下沉加速度曲线与实际略有偏差,如图3a所示。因此对式(3)做进一步优化:首先用参数H,K分别表示Δt和A的指数,选用《建筑物、水体、铁路及主要井巷煤柱留设与压煤开采规程》中4组矿区数据[18],采用式(4)计算出下沉时间,见表1。
表1 各矿区参数
Table 1 Parameters of each mine area

矿井vt/(m·d-1)r/mω0/m下沉时间/d东梁矿二井1.047.872 30.651 9119.743 7清河门三坑1.624.545 50.920 943.783 5大磁矿221111.533.613 40.719 660.747 9十一井2.092.400 04.741 4137.271 2
注:vt为工作面推时速度;r为主要影响半径。
当地表下沉前和下沉达到最大值后的下沉速度都为零,且连续6个月下沉值不超过30 mm时(即下沉速度vx为0.000 16 m/d),可认为地表移动期结束[19]。便于计算,取下沉速度为0.000 1 m/d时,认为是地表下沉初始和结束阶段,因此令 vx(t0)=0.000 1,求出2个t0即为下沉速度等于0.000 1 m/d的时间,|t1-t2|即地表从开始下沉到下沉达到最大值的时间T,即
(4)
将每个矿区数据代入式(3),并取不同指数绘制下沉图像,结果如图4所示,当指数H=4时,下沉量达到最大时对应的时间与采用概率积分法计算出的时间最为接近,且指数K与下沉时间成正比关系。因此,为简化模型,令H=4,K为待拟合参数。便于表示,令t=0,Δt表示为t,得出式(5)为地表下沉的初始式。式(5)的下沉曲线,下沉速度曲线,下沉加速度曲线如图3b所示,即

图3 优化前后变异函数的下沉、速度、加速度曲线
Fig.3 Subsidence,velocity and acceleration images of variograms before and after optimization
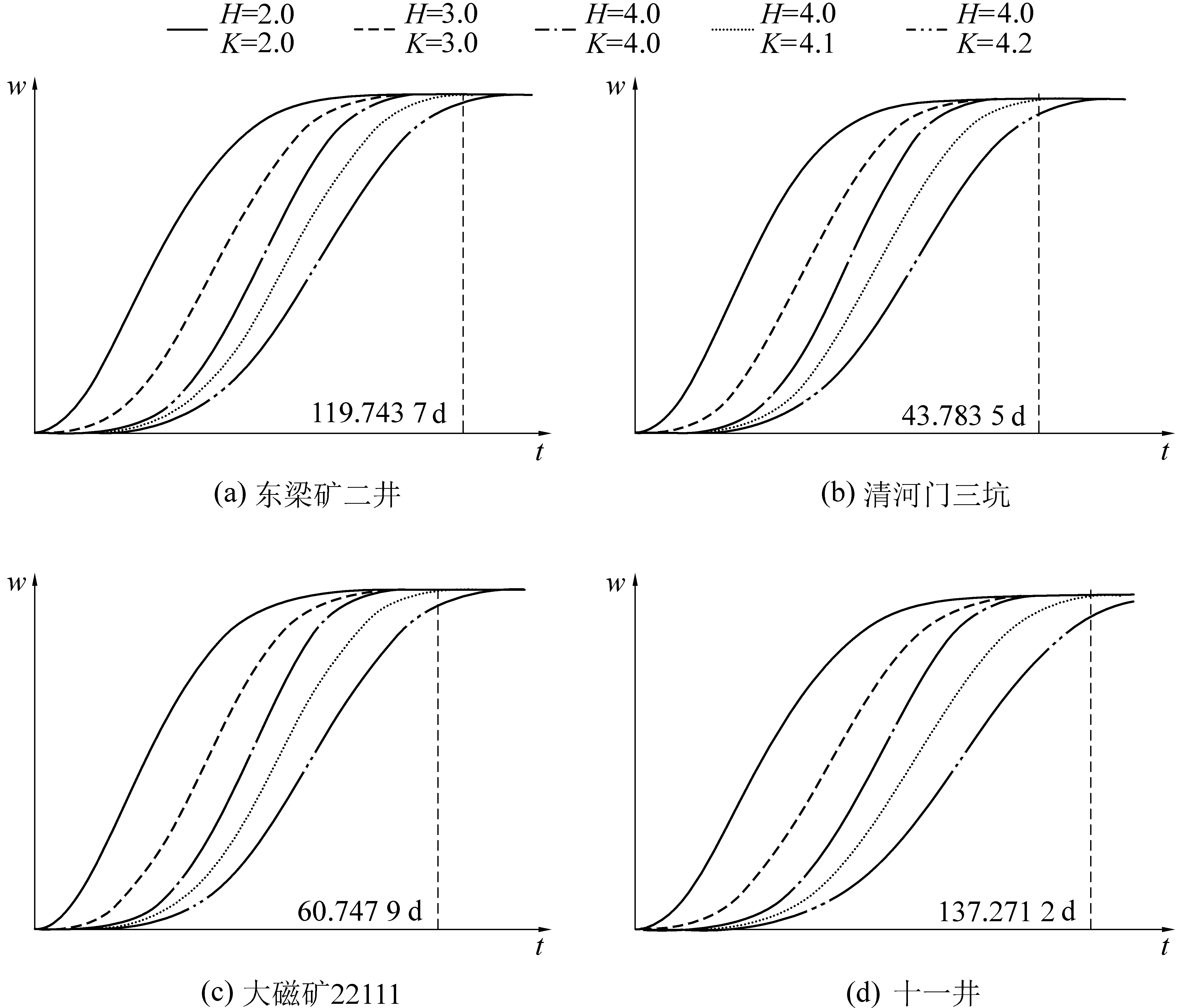
图4 不同指数的模型曲线
Fig.4 Model curves for different exponentials

(5)
由图2可知,地表从开始下沉到下沉达到最大值的时间(即曲线达到最大值C0+C)为![]() 。下沉所用的时间可以通过概率积分法相关知识求解,得式(6)概率积分法下沉式,即
。下沉所用的时间可以通过概率积分法相关知识求解,得式(6)概率积分法下沉式,即
(6)
将式(6)中的工作面推进距离s由推进速度vt和推进时间t表示,可得出概率积分时间函数模型,即式(7)
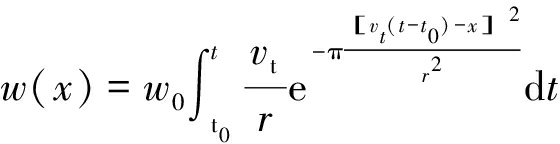
(7)
式中:r为主要影响半径,m;s为工作面推进距离,m;x为地表检测点坐标,m;t为开采时间,d;t0为监测点开始下沉的时间,d。
将式(7)对t求导可求出基于概率积分法的下沉速度式为
(8)
其中,![]()
下沉时间T与变程间的关系有,注意到![]() 所以
所以![]() 并代入(4)式可得到基于变异函数的开采沉陷下沉预计函数模型,即
并代入(4)式可得到基于变异函数的开采沉陷下沉预计函数模型,即

(9)
式(9)对t求导可求出地表下沉速度式为
![]()
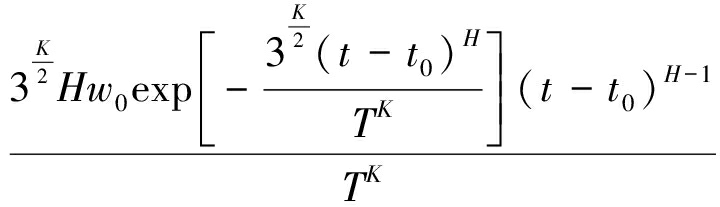
(10)
式(10)对t求导可求出地表下沉加速度式为
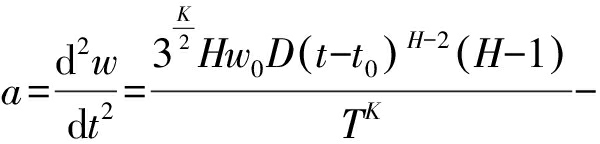
![]()
(11)
其中,
2 应用分析
2.1 实例一
为了验证模型的适用性和可靠性,选取某矿区2038工作面[20]作为研究对象,该工作面采用长壁全陷开采,上覆岩层为坚硬型覆岩。工作面走向长980 m,倾斜长165 m,以开切眼为坐标原点,走向线上监测点距离开切眼的距离为横坐标x,选取走向线23号点(x23=455 m)、28号点(x28=545 m)、34号点(x34=636 m)的测量结果与预计结果进行对比分析,采用均方误差(m)和相对中误差(f)作为衡量预计精度的标准,见式(12)、式(13)为
(12)
(13)
矿区相关参数见表2,采用基于变异函数的预计模型分别对23号点位、28号点位和34号点位下沉量、下沉速度、下沉加速度进行预计,预计曲线如图5、图6、图7所示,同时与实测数据进行误差对比分析,结果见表3。其中实测下沉速度vs以及对应时间的计算方法见式(14)、式(15),实测下沉加速度0.5单位以及对应时间的计算方法见式(16)、式(17)。

图5 23号点下沉量、下沉速度、下沉加速度
Fig.5 Subsidence,velocity and acceleration images at point 23

图6 28号点下沉量、下沉速度、下沉加速度
Fig.6 Subsidence,velocity and acceleration images at point 28

图7 34号点下沉量、下沉速度、下沉加速度
Fig.7 Subsidence,velocity and acceleration images at Point 34
表2 地表沉降动态参数
Table 2 Dynamic parameters of surface subsidence

vt/(m·d-1)r/mKM/mqθ/(°)t0/d(点23/28/34)4.52104.3130.54988/109/129
注:r为主要影响半径;M为开采厚度;q为下沉系数;θ为煤层倾角;t0为监测点下沉起始时间。
(14)
(15)
(16)
(17)
式中:wi为第i次监测的下沉值,m;wi-1为第i-1次监测的下沉值,m;tw,i和tw,i-1分别为wi、wi-1对应的监测时间,d;tv为下沉速度对应的时间,d;vi、vi-1、tv,i、tv,i-1、ta同理。
由表3可知,23号点不同时间下沉预计的均方误差为0.027 m,相对中误差为1.69%;28号点不同时间下沉预计的均方误差为0.026 m,相对中误差为1.62%;34号点不同时间下沉预计的均方误差为0.039 m,相对中误差为2.44%。根据实测资料计算分析,23号点最大下沉速度出现的时间段为第153 d到第183 d,为期30 d下沉了0.682 m,其下沉速度为0.022 70 m/d;28号点最大下沉速度出现的时间段为第183 d到第223 d,为期40 d下沉了0.896 m,其下沉速度为0.022 40 m/d;34号点最大下沉速度出现的时间段为第223 d到第250 d,为期27 d下沉了0.594 m,其下沉速度为0.022 00 m/d。变异函数模型计算出来的最大下沉速度为0.023 77 m/d。通过式(18)可计算模型预计最大下沉速度(vp)与实测最大下沉速度vs分别相差4.7%、6.1%、8.0%,下沉速度与下沉加速度预测精度见表4,由于采用取中值的方法计算下沉速度和加速度时间点,因此存在一定的误差,下沉加速度的计算更是由于误差累计使得预计与实际相差较大。
表3 23、28、34号点下沉量实测值与预测值对比
Table 3 Comparison between measured data and prediction data of subsidence at point 23,28,34

表4 23、28、34号点实测值与预测值对比
Table 4 Comparison between measured data and prediction data of subsidence at Point 23,28,34

项目23号点mf/%28号点mf/%34号点mf/%下沉速度vx/(m·d-1)0.001 46.160.001 04.460.001 46.36加速度/(m·d-2)2.52×10-442.112.94×10-476.093.48×1080.86
(18)
2.2 实例二
某矿5034工作面,走向长1 303 m,回采时间为2016年9月—2017年6月,工作面采用综采(走向长壁一次性采全高)采煤工艺,观测时间为2017年1月—2018年5月。观测站的布设从距离开切眼546 m处开始布设。坐标系以沿观测线起点为原点。由于只布设了半条观测线(未开采部分),所以下沉曲线图只有一半,因此重点对该部分进行预计。工作面参数见表5。因为地表下沉在2018年3月29日达到稳定,故选取之前5个时间点下沉量进行对比,如图8所示。
表5 地表沉降动态参数
Table 5 Dynamic parameters of surface subsidence

vt/(m·d-1)r/mKM/mqθ/(°)4.212535.820.773
实测下沉量与本文模型预计结果如图8所示,模型预计下沉满足地表下沉一般规律,预计下沉过程与实测基本符合。但实测下沉盆地处呈现凸型,其原因可能为在布设观测线时,该区域已发生下沉。

图8 走向线地表动态下沉
Fig.8 Surface dynamic subsidence of strike line
3 结 论
1)分析现有模型存在的问题:参数单一、最大下沉速度对应的下沉值与最大下沉值的比值为定值、下沉速度与下沉加速度曲线与实际地表下沉速度与加速度不符。
2)应用概率积分法推导出地表下沉时间式,并应用变异函数模型结合地表下沉时间式建立了下沉模型。通过对不同指数的下沉模型对比分析,得出结论:当模型分子的指数H=4时,预计下沉时间与采用概率积分法计算出的时间最为接近,且分母指数K与下沉时间成正比关系,因此采用H=4,K为待拟合参数的方法建立半无限开采地表下沉动态预计模型。
3)通过实例验证,对比分析出基于变异函数的预计模型对2038工作面3组数据的下沉量、下沉速度和下沉加速度的预计中其形态不仅符合地表下沉规律,而且下沉量的均方误差最大为0.039 m,最小为0.026 m;相对中误差最大为2.44%,最小为1.62%;下沉速度均方误差最大为0.001 4 m/d,最小为0.001 0 m/d;相对中误差最大为6.63%,最小为4.46%;最大下沉速度误差最大为8.0%,最小为4.7%。但由于计算方法以及累计误差导致由实测下沉量计算的下沉加速度与预计结果相差较大。5034工作面走向线的下沉预计满足地表下沉规律,能够描述地表随时间变化的动态过程。
[1] 朱广轶,沈红霞,王立国.地表动态移动变形预测函数研究[J].岩石力学与工程学报,2011,30(9):1889-1895.
ZHU Guangyi,SHEN Hongxia,WANG Liguo.Study of dynamic prediction function of surface movement and deformation[J].Chinese Journal of Rock Mechanics and Engineering,2011,30(9):1889-1895.
[2] 崔希民,缪协兴,赵英利,等.论地表移动过程的时间函数[J].煤炭学报,1999,24(5):453-456.
CUI Ximin,MIAO Xiexing,ZHAO Yingli,et al.Discussion on the time function of time dependent surface movement[J].Journal of China Coal Society,1999,24(5):453-456.
[3] 常占强,王金庄.关于地表点下沉时间函数的研究—改进的克诺特时间函数[J].岩石力学与工程学报,2003,22(9):1496-1499.
CHANG Zhanqiang,WANG Jinzhuang.Study on time function of surface subsidence the improved Knothe time function[J].Chinese Journal of Rock Mechanics and Engineering,2003,22(9):1496-1499.
[4] 胡青峰,崔希民,康新亮,等.Knothe时间函数参数影响分析及其求参模型研究[J].采矿与安全工程学报,2014,31(1):122-126.
HU Qingfeng,CUI Ximin,KANG Xinliang,et al.Impact of parameter on Knothe time function and its calculation model[J].Journal of Mining & Safety Engineering,2014,31(1):122-126.
[5] 张 兵,崔希民.开采沉陷动态预计的分段Knothe时间函数模型优化[J].岩土力学,2017,38(2):541-548,556.
ZHANG Bing,CUI Ximin.Optimization of segmented Knothe time function model for dynamic prediction of mining subsidence[J].Rock and Soil Mechanics,2017,38(2):541-548,556.
[6] 何国清,马伟民,王金庄.威布尔分布型影响函数在地表移动计算:用碎块体理论研究岩移基本规律的探讨[J].中国矿业学院学报,1982,27(1):4-23.
HE Guoqing,MA Weimin,WANG Jinzhuang.Application of influence function of Weibull distribution to the precalculation of ground surface movement:a study on the fundamental law of ground movement based on the clastic theory[J].Journal of China Institute of Mining and Technology,1982,27(1):4-23.
[7] 涂许杭,王志亮,梁振淼,等.修正的威布尔模型在沉降预测中的应用研究[J].岩土力学,2005,26(4):621-623,628.
TU Xuhang,WANG Zhiliang,LIANG Zhenmiao,et al.Study on application of modified Weibull model to settlement prediction of foundation[J].Rock and Soil Mechanics,2005,26(4):621-623,628.
[8] 王 伟,卢廷浩.基于Weibull曲线的软基沉降预测模型分析[J].岩土力学,2007,28(4):803-807.
WANG Wei,LU Tinghao.Study on prediction model of soft foundation settlement based on Weibull curve[J].Rock and Soil Mechanics,2007,28(4):803-807.
[9] 李春意,高永格,崔希民.基于正态分布时间函数地表动态沉陷预测研究[J].岩土力学,2016,36(S1):108-116.
LI Chunyi,GAO Yongge,CUI Ximin.Progressive subsidence prediction of ground surface based on the normal distribution time function[J].Rock and Soil Mechanics,2016,36(S1):108-116.
[10] 张 兵,崔希民,胡青峰.开采沉陷动态预计的正态分布时间函数模型研究[J].煤炭科学技术,2016,44(4):140-145,174.
ZHANG Bing,CUI Ximin,HU Qingfeng.Study on normal distributed time function model to dynamically predict mining subsidence[J].Coal Science and Technology,2016,44(4):140-145,174.
[11] 张 凯,胡海峰,廉旭刚,等地表动态沉陷预测正态时间函数模型优化研究[J].煤炭科学技术,2019,47(9):235-240.
ZHANG Kai,HU Haifeng,LIAN Xugang,et al.Optimization of surface dynamic subsidence prediction normal time function model[J].Coal Science and Technology,2019,47(9):235-240.
[12] 谢广祥,常聚才,华心祝.开采速度对综放面围岩力学特征影响研究[J].岩土工程学报,2007,29(7):963-967.
XIE Guangxiang,CHANG Jucai,HUA Xinzhu.Influence of mining velocity on mechanical characteristics of surrounding rock in fully mechanized top-coal caving face[J].Chinese Journal of Geotechnical Engineering,2007,29(7):963-967.
[13] 王方方,李鹏宇,路绪杰.开采速度与地表动态下沉速度及加速度的关系模型研究[J].测绘与空间地理信息,2018,41(10):207-210.
WANG Fangfang,LI Pengyu,LU Xujie.Research on the speed and surface mining subsidence velocity and acceleration of dynamic relationship model[J].Geomatics & Spatial Information Technology,2018,41(10):207-210.
[14] 贾新果,宋桂军,陈 凯.工作面推进速度对地表沉陷动态变形影响研究[J].煤炭科学技术,2019,47(7):208-214.
JIA Xinguo,SONG Guijin,CHEN Kai.Study on influence of mining face advancing velocity on progressive surface subsidence and deformation[J].Coal Science and Technology,2019,47(7):208-214.
[15] 宁永香,焦希颖.回采速度对地表动态移动变形值的影响[J].煤炭科学技术,2004,32(11):74-76.
NING Yongxiang,JIAO Xiying.Ming speed influenced to surface ground dynamic displacement and deformation[J].Coal Science and Technology,2004,32(11):74-76.
[16] 黄乐亭,王金庄.地表动态沉陷变形的三个阶段与变形速度的研究[J].煤炭学报,2006,31(6):420-424.
HUANG Leting,WANG Jinzhuang.Study on the three stages and deformation velocity of dynamic surface subsidence deformation[J].Journal of China Coal Society,2006,31(6):420-424.
[17] 林振山,袁林旺,吴得安.地学建模[M].北京:气象出版社,2003:111-113.
[18] 国家煤炭工业局.建筑物、水体、铁路及主要井巷煤柱留设与压煤开采规程[M].北京:煤炭工业出版社,2000:121-129.
[19] 谢飞鸿,张立杰.开采沉陷可视化计算方法与工程应用[M].北京:煤炭工业出版社,2015:70.
[20] 郭旭炜,杨晓琴,柴双武.分段Knothe函数优化及其动态求参[J/OL].岩土力学,2020(6):1-8[2020-05-21].https://doi.org/10.16285/j.rsm.2019.1567.
GUO Xuwei,YANG Xiaoqin,CHAI Shuangwu.Optimization of segmented Knothe function and its dynamic parameter calculation[J/OL].Rock and Soil Mechanics,2020(6):1-8[2020-05-21].https://doi.org/10.16285/j.rsm.2019.1567.
