与该时刻破断的承载结构所释放变形能
之差，而在描述弹性能方面更具合理性，并给出了该指标基于荷载-时间曲线和声发射的实测计算路径，为获得更为准确的弹性能描述做出了有益探索。摘 要：现有冲击倾向性测试结果常表现出与冲击地压事故互为不充分不必要条件的关系，对于工程的参考价值有待进一步提高。为此，从冲击倾向性描述弹性能的本质出发，构建了从功能上能够还原弹性能积聚与释放的统计损伤物理模型，从基本物理行为的角度对应力-应变曲线的升降趋势，以及加载过程中能量的积聚与耗散进行了研究。结果表明：外载做功和能量释放贯穿加载全过程，目前以应力-应变曲线峰前、峰后段的相关特征分别描述弹性能积聚和耗散的方式能够简化计算，但未能反应真实的力学行为，基于物理模型进一步指出，试件的变形势能增量ΔWti本质上是当前时刻试件中仍具承载能力结构新增的变形能与该时刻破断的承载结构所释放变形能之差，而在描述弹性能方面更具合理性，并给出了该指标基于荷载-时间曲线和声发射的实测计算路径，为获得更为准确的弹性能描述做出了有益探索。
移动扫码阅读
Abstract:The current test results of coal seam bursting tendency and coal bump accident are mutually inadequate and unnecessary conditions.The test results of bursting tendency need to be further improved for the reference value of coal mining.From the essence of bursting tendency to describe elastic energy, this study establishes a statistical damage physical model that can restore the accumulation and release of elastic energy.The rising and falling trend of stress-strain curve, the energy accumulation and dissipation during loading are studied from the perspective of basic physical behavior.The results show that external load work and energy release run through the entire loading process, and the current ways of describing the accumulation and dissipation of elastic energy with the characteristics of the pre-peak and post-peak sections has advantages in simplifying the calculation, but fail to reflect the true underlying physical logic.Based on the physical model, it is pointed out that the increase in deformation potential energy of the specimen ΔWti is essentially the difference between the new deformation energy 
is more reasonable in describing the elastic performance.The calculation method of the index based on the load-time curve and the acoustic emission information is derived, which is a useful exploration for obtaining more accurate elastic energy.
煤的冲击倾向性描述的是煤体具有积聚变形能并产生冲击破坏的一种性质[1-4]，从具体力学行为的角度，该性质描述的是煤在受载条件下积聚弹性变形能的能力和失稳破坏时弹性能释放的剧烈程度。与之同样重要的概念是冲击危险性，即真实工程场景下发生冲击地压的危险性或可能性[5-7]。但根据已有的事故案例，煤体具有冲击倾向性并不意味着一定会发生冲击地压，而发生冲击地压的案例中，煤体也不一定具有冲击倾向性，二者高度相关但又互为不充分不必要条件。
煤岩介质的力学行为与应力环境密切相关，而冲击倾向性则是在国家标准要求的统一加载条件下获得的，其中，动态破坏时间(DT)和弹性能指数(WET)为应力加载，速度0.5～1.0 MPa/s，而冲击能量指数(KE)由于需要全应力-应变曲线，需要采取位移加载，速度为0.5×10-5～1.0×10-5 mm/s[8]。这种测试方式能够为定性认知相近加载条件下，不同煤样冲击倾向性的相对强弱提供参考。但工程实际中的荷载变化区间更大、应力加载路径更多，而正是标准加载条件与实际加载条件的差异，造成了冲击倾向性测试结果与实际情况互为不充分不必要条件的现状。
狭义而言，标准测试条件下获得的结果才可被称为冲击倾向性，但若仅局限于此，造成上述不充分不必要关系的根源将只是冲击倾向性测试并未充分反映实际加载环境的多样性而已。冲击地压作为工程科学问题，对其研究的根本目的是为了在实际工况下降低或消除冲击危险性，简单地在概念或方法层面进行调整，而不深究其底层物理逻辑，显然满足不了有效防控的根本需求。
煤岩的特殊细观结构是造成其对于力学环境敏感的主要原因[9]，更具针对性地，细观结构与冲击倾向性的高度相关性也已得到验证，如煤的显微硬度、显微脆度、显微组分、原始损伤等细观特征与冲击倾向性呈正相关[10]；不同冲击倾向性煤样的细观结构在空间特征上存在显著差异；通过CT扫描获取单位面积裂隙周长、面积分数等统计性指标可实现对于冲击倾向性的定性评价等[11]。因此，对于冲击倾向性的底层物理逻辑，现有研究事实上已经给出了合理的关注方向。然而，煤岩具体力学行为是在应力、结构以及物性因素的共同作用下产生[12]，尤其对于细观结构的研究，目前还远未达到定量水平，由此带来的复杂度和制约性[13-14]使得尚未有成果能有效地将已获得的物理逻辑认知应用到具体的工程实践中去。
为此，笔者以挖掘冲击倾向性底层物理逻辑的工程指导路径为目标，通过分析现有冲击倾向性指标的设计特点，提出了在功能上能够反映弹性能积聚和释放的弹性损伤模型，并据此指出了冲击倾向性更为准确的物理内涵，依据简单可测的原则，给出了更接近真实情况的能量积聚和释放的监测手段、计算方法，为强化研究成果的工程指导能力做出了有益的探索。
冲击倾向性是对标准加载条件下煤样某种特定力学行为的概括描述，但为方便阐述其本质，同时避免新名词造成理解混乱，约定本文所述“冲击倾向性”不局限于标准加载条件。
冲击倾向性既然描述的是某种力学行为，依靠应力-应变曲线进行相关指标的设计是极为自然的，而现有指标也正是按照这一思路开展相关工作，并同时考虑了弹性能积聚和释放的描述。
目前，按照指标所关注的物理内涵不同，鞠文君等[15]将冲击倾向性指标划分为强度指标、时间指标、刚度指标、变形指标和能量指标，并列出了具体指标的计算方法，部分指标见表1。
表1 冲击倾向性代表性描述指标
Table 1 Representative description index of bursting tendency
序号类别评价指标计算方法图解1强度指标单轴抗压强度σc[8]在常规单轴加载条件下,试件所能承受最大载荷与其横截面之比
续表
序号类别评价指标计算方法图解2时间指标动态破坏时间DT[8]煤试件在单轴压缩状态下,从极限强度到完全破坏所经历的时间3刚度指标下降模量指数DMI[16]DMI=E/M(E为峰前弹性模量,取0.5倍单轴强度处加载曲线切线斜率;M为峰后软化模量)4变形指标弹性变形指数KεE[17]KεE=εe/εp(εe为峰前弹性应变;εp为峰前塑性应变)5能量指标弹性能量指数WET[8,18-19]WET=ϕSE/ϕSP(ϕSE为卸载时积累的弹性应变能;ϕSP为卸载时耗散的塑性应变能;WET反映试件受载过程弹性应变能的积累能力)剩余能量指数WR[20]WR=(WE-W2)/W2WE=∫BAσd(ε/∫AOσdε)∫COσdε(WE为峰前积累弹性应变能;W2为峰后耗散应变能;σ为应力;εA、εB、εC、εD为A、B、C、D点应变;分别ε为应变;WR表征剩余能量与稳定破坏耗散能量相对关系)峰值能量冲击性指数KEV[21] KEV=WE/W2有效弹性能释放速率指数KET[22] KET=WSE-WXDT (WSP为峰值强度时刻试件中累计耗散的能量;WSE为峰值强度时刻试件中积累弹性能;WW为峰后的能量耗散)
文献对于冲击倾向性指标的相关研究做了较为详细的统计，由表1可直观地看出，目前常用的冲击倾向性指标设计基本全部依赖于应力-应变曲线，而依据不同加载控制方式所获得的应力-应变曲线则具有不同的描述功能：应力控制加载，可获得动态破坏时间等峰后跌落特性；位移控制加载，用以获得全应力-应变曲线；与前2种方式配合的循环加卸载，用以获得峰前弹性应变等指标。冲击地压的本质是弹性应变能的积聚和释放，循环加卸载和位移控制由于能够更好地支撑应变能计算而较多单独或配合使用。
循环加卸载的优势在于能够通过卸载和回弹，获得弹性段某加载点对应的真实弹性能积聚和耗散，进而评价介质存储弹性能的能力，但卸载点需要预估以保证加载处于试件的弹性阶段，从而在操作层面具有一定难度，同时，计算时通常期望获得峰值点前全部的弹性能积聚与耗散情况，在实际操作不可能的前提下，多假设峰前加载点对应的弹性能与总应变能的比值为常量，用之乘以峰值点前总的应变能，而获得而峰值点处介质存储弹性能的估算值，见表1中剩余能量指数WR。
位移控制可获得全应力-应变曲线，进而提供较为丰富的峰前、峰后力学行为细节，但目前多默认峰前为应变能积聚，而峰后为能量耗散，如冲击能量指数，也有将循环加卸载与位移加载结合，提高峰前弹性能计算的准确性。但客观事实是，应变能的积聚和耗散是伴随整个加载过程的行为，简单将峰前作为积聚或峰后作为耗散进行处理，在提供定性参考方面可能没问题，但由此也会使得一些细节被忽略，进而造成类似于冲击倾向性评价结果与实际危险性不符的情况。
综上，现有冲击倾向性指标的设计基本上全部依赖于应力-应变曲线，而设计的基本原则是期望准确描述加载过程中弹性能积聚和耗散的情况，循环加卸载和全应力-应变曲线是实现上述目标的有效手段，而需要关注的是，目前多将峰前作为应变能积聚阶段、峰后作为应变能耗散阶段处理，该做法能够定性描述介质存储弹性能的能力，但由于与客观事实不符，存在造成一定误导的可能，因此，有必要从还原客观物理行为的角度，明确冲击倾向性的本质，进一步提高冲击倾向性鉴定结果的可靠性。
应变能多通过应力-应变曲线的线下积分获得，直观上是对曲线形态的一种描述，而现有指标设计多离不开对于峰值点的关注，峰值点作为曲线的拐点，其前后升降的物理内涵，将是揭示冲击倾向性本质的切入点。
首先，需要明确每个加载时刻前后所发生的力学行为，为此，需要构建能够反映介质受载基本行为的物理模型。对于冲击倾向性鉴定，多采用单轴加载，为描述方便，将模型的设计背景限定为位移控制的单轴加载。从能量角度，试件受载过程是试验机对其做功的过程，试件将产生2种主要响应，即能量积聚和耗散，前者来自于试件中完整部分的持续变形，后者来自于裂隙的发育、结构面间的摩擦、细观结构的破断等，其中，以结构破断所释放的能量为主，因此，本物理模型的核心功能侧重于介质的变形和破断。
此外，煤岩结构极为复杂，目前还尚未找到具有较好兼容性的量化描述方法，笔者将其简化为沿圆心均匀分布的理想弹脆性杆件。综上，试件可表征为统计损伤物理模型，其结构如图1所示。
图1 统计损伤物理模型
Fig.1 Statistical damage physical model
其假设包括：
1)图中杆件共计N个，且所有杆件长度L和截面积s均相同。
2)按照承载极限最大值σmax和最小值σmin，依次将杆件均匀划分为M档，其中，第一档杆件承载极限σ1=σmin，第M档杆件承载极限σM=σmax，第j档(j∈[1，M])杆件数量为nj根，同档杆件围绕圆心均匀分布。
3)第j档杆件承载极限均为σj，弹性模量均为Ej，由此，每档的临界破断应变为εj=σj/Ej，并规定εa>εb(a,b∈[1，M]且a>b)，以此保证同档杆件同时破坏。
在明确模型基本假设后，将对模型施加位移控制的荷载，加载速率为u，加载时间按照时步计算，第i个时步记为ti。由此，若加载至ti时刻，1～(m-1)档杆件全部破坏，则该时刻试件所承受荷载为
(1)
类似地，ti+1时刻，随加载导致新增Δm档杆件破坏，则对应荷载
(2)
记Δt=ti+1-ti，则该时间段内荷载新增
ΔP=Pti+1-Pti=
(3)
显然，对应于荷载位移曲线，若ΔP>0，则曲线表现为上升，反之下降，峰值点处该指标为0。新增荷载ΔP由2部分决定，首先是ti～ti+1时步内尚未破坏的第(m+Δm)～M档杆件产生单位时步应变，即uΔt/L，所需新增外部荷载的总和，需要注意的是，每根杆件产生单位时步应变所需的荷载uEsΔt/L为常量；其次是ti～ti+1时步内新增破坏的Δm档杆件，产生累积应变uti/L所需的荷载，由于符号为负，故可将其理解为反力。
若Δt为常量，则有
ti=iΔt
(4)
则式(3)简化为
(5)
进一步考虑能量特征，由于每根杆件的截面s和长度L相同，故每根杆件的体积V为
V=sL
(6)
则ti时刻试件产生uti变形，该时刻模型的变形势能Wti为
(7)
类似的，ti+1时刻模型的变形势能Wti+1为
(8)
则每时步模型能量状态的增量ΔWti+1为
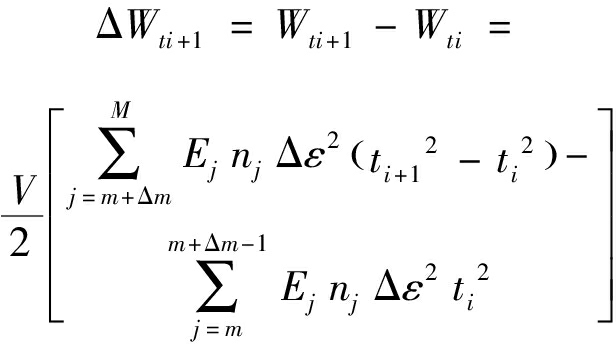
(9)
令仍具承载能力结构新增变形能ΔW′ti+1为
(10)
令该时刻破断的承载结构所释放的变形能ΔW″ti+1为
(11)
则
(12)
从式中可以看出，每一时步内都会出现Δm档杆件破断，同时剩余杆件仍在承载的状况，而弹性能也是在部分杆件继续承载、部分杆件断裂的过程中逐渐累积，这与真实情况相符。
进一步观察等式右侧，
的物理内涵可表述为：使ti+1时刻仍处于承载状态的第(m+Δm)～M档杆件，产生Δε应变所需新输入的能量，若对应结构的承载能力，与其完整性或弹性状态等价，则该部分能量转化为弹性势能；
的物理内涵可表述为：该时刻Δm档杆件破断所释放的能量。其中，前者是增量，即ti+1时刻尚处于完整状态的承载结构新增的弹性能；而后者是累积量，即破断杆件会释放掉其前期ti时长内积累的所有弹性能。
公式整体的物理意义可表述为：在考虑试件中承载结构变形和破断同时发生的前提下，令试件整体产生ΔtΔu位移时外载做所的功，等于该时步试件中仍具有承载能力结构中新增的变形能，与该时步破断承载结构所释放的变形能之差。由此，从理论上给出了外部荷载作用下，相邻时刻模型能量状态变化所对应的物理行为细节。
需要特别注意的是，项的物质载体是当前时步仍然具有承载能力的完整结构，对应于真实情况，正是冲击倾向性所关注弹性能的理想载体，进而有望据此获得更为准确的弹性能描述方法。
ti时刻模型变形能Wti，上述模型通过累加尚处于承载状态的杆件变形能获得，相关参量不可实测。但注意到
(13)
(14)
式中：εi为i时刻的杆件应变；σij为i时刻j档杆件单根应力。
将式(6)、式(13)、式(14)代入式(7)可得
(15)
而j档杆件所承受荷载Pij为
(16)
ti时刻杆件所产生的位移Si为
Si=Lεi
(17)
代入后可得
(18)
而式中
项表示尚处于承载状态的所有杆件的总荷载，宏观上即为物理模型当前时刻的外载值P，由此
(19)
若不考虑承载结构空间形态的影响，即认为试件承载能力全部由结构的完整性来提供，则实测所得荷载Ps即可以用来表征P，由此，实现了Wti的可测，进而得到ΔWti的数值及演化曲线。
同样，通过物理模型可知，单位时间内的能量释放是由杆件破坏所引起，而真实条件下的细观结构破断将会以声发射的形式被捕捉到。虽然不能完全将声发射与能量耗散对等，但声发射的能量本质使其天然与真正的能量耗散存在显著的正相关性，同时也使其对于能量耗散的描述能更为直接，由此，采用ti时刻的声发射量值WtiEA表征
具有合理性。
由此，基于荷载-位移曲线和式(19)实现了ti时刻变形势能Wti的实测，进而获得ΔWti；以ti时刻的声发射能量表征该时刻的能量释放
若将细观结构具备承载能力，与其处于弹性状态等价，则根据式(12)，ti时刻仍处于承载状态的细观结构，所产生的弹性势能增量为
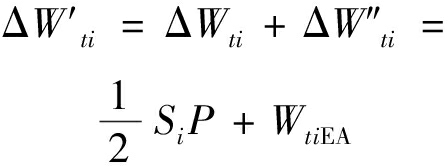
(18)
进而实现了模型由ti时刻向ti+1时刻变形过程中，完整介质中变形势能增量的实测，基于变形势能增量则可进一步计算累计变形势能。
随机选取具有复杂变化趋势的煤样，以验证上述方法的可操作性。该煤样在0.1 mm/min的位移加载条件下被压至破坏，其荷载-时间曲线如图2所示。
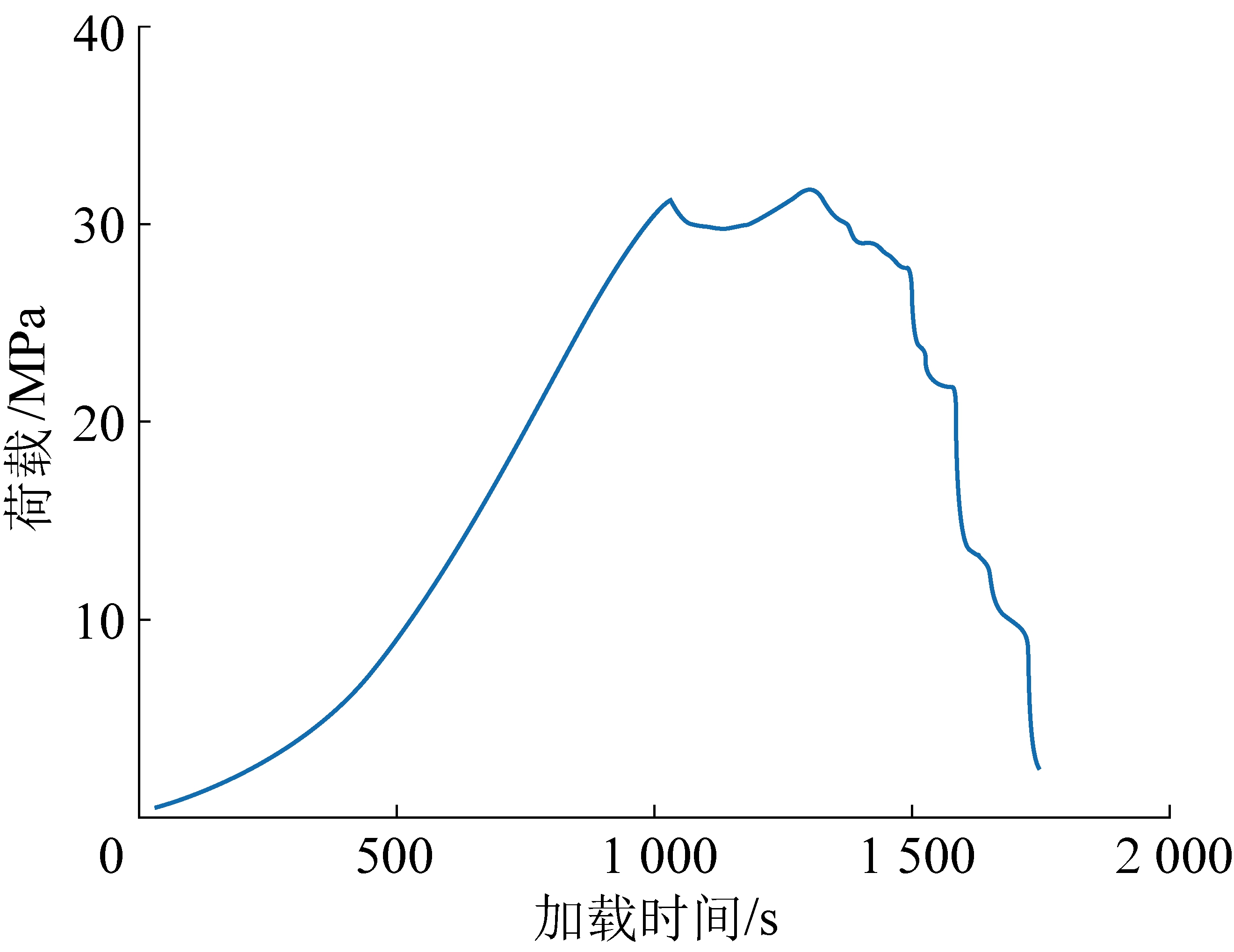
图2 验证试验荷载-时间曲线
Fig.2 Load-time curve of verification test
由图2可得，该试样表现出了较为复杂的荷载演化特征，若基于传统的弹性能计算方法，则会加入较多的主观因素影响，例如动态破坏时间中峰值点和跌落终点的选取。而通过计算变形能增量
监测声发射能量WtiEA，则能够获得全过程的数据进行相关的计算，为方便展示，将所有数据进行归一化处理以消除量纲,并以归一化后的时间序列为横坐标绘制曲线如图3所示。
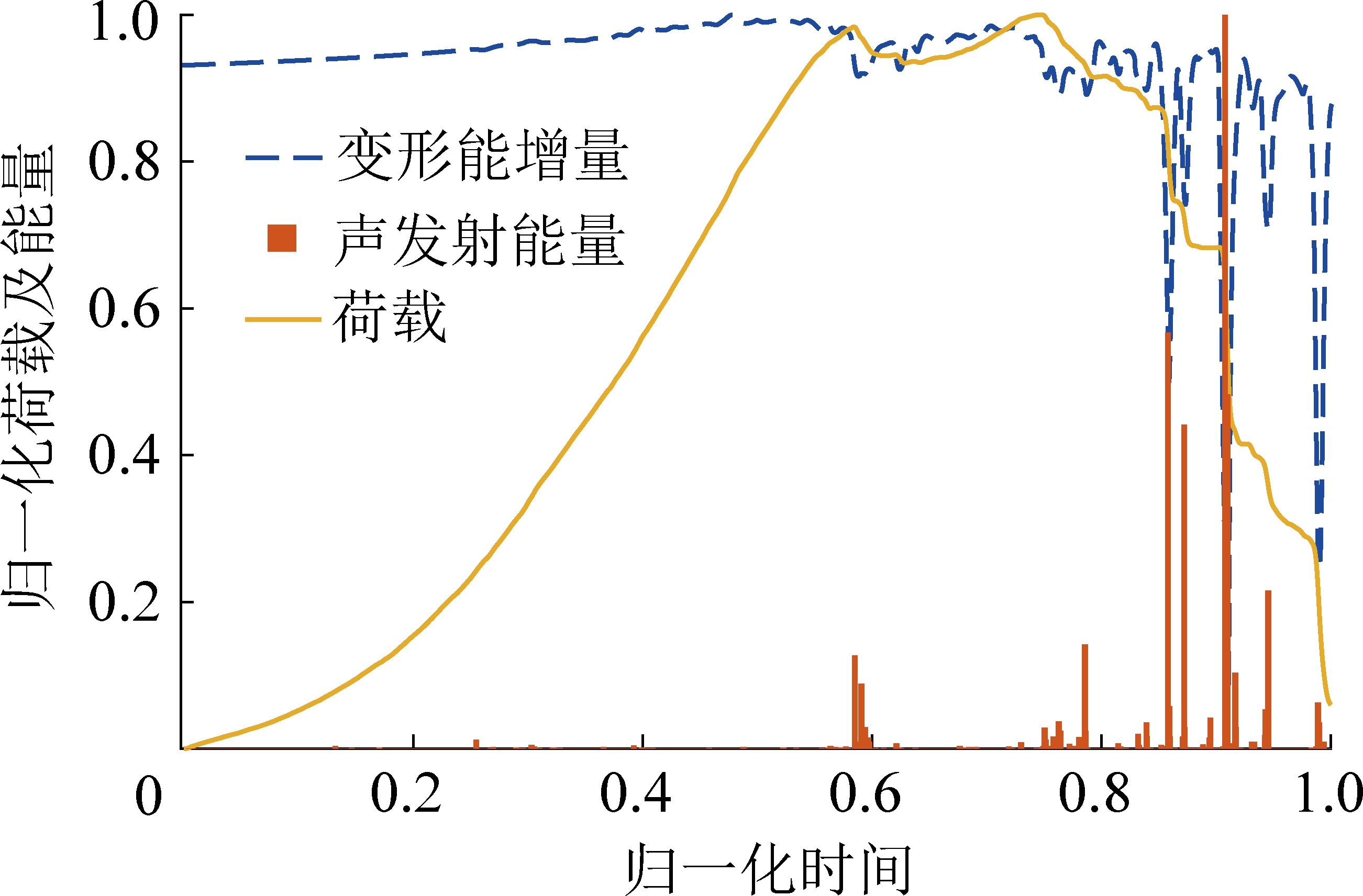
图3 变形能及声发射能量归一化结果
Fig.3 Results of variable situation energy and acoustic emission information normalization
由图3可得，基于提出的弹性势能增量计算方法，配合声发射监测，能够实现ΔWti和
的测量，进而获得了弹性势能增量
的实测值，其优势在于，使得介质弹性能存储及释放相关性质的评价工作，不再拘泥于应力-应变曲线简单的峰前、峰后划分，相关指标的设计也不再局限于各种线下积分的比值，而是从真实的物理行为角度，给出了相关参量的实测方法，降低了面对复杂趋势曲线划分相关节点时的主观因素影响。同时，由于和是动态可测的物理量，进而在原理上支持了弹性变形能动态评价的可行性，为工程尺度实现对于煤体弹性能集中度的动态获取提供了可靠路径。
此外，依靠荷载-位移曲线获得的变形能增量，与依靠声发射测量的破裂事件能量，两种独立的测量手段在演化趋势上表现出了较强的对应性，从某种程度上暗示了该方法的潜在价值，但目前声发射监测设备所得的能量多利用门限电压上方的波形包络线计算，其单位是ms×mV(毫秒×毫伏)，并不能与加载所产生的变形势能(量纲为J，焦耳)直接进行融合计算，优化声发射事件能量计算方法，定制开发相关监测设备也是未来的攻关方向。
上述工作将试件受载情况下的物理逻辑反映到了变形能的计算当中，同时引入了声发射信息，在一定程度上逼近了弹性能真实值的实际测量，能够为后续的相关指标设计提供底层原理支撑。但煤岩本身的复杂性，使得该项工作也仅是在变形能测量模式上取得了有限进展。
目前的制约在于，无论是对于细观结构空间特征的描述还是针对其空间特征力学效应的试验，通常都采用了简化的手段以降低研究难度，而煤岩的复杂性体现在其随机多变的裂隙等结构要素上，上述简化操作恰恰忽略了这一关键因素，如裂隙发育对于结构强度的弱化作用，细观结构破断对于周边结构所产生的连带影响等，也正是由于此类的简化导致了室内测试结果对于工程实际参考性较弱的现状。
煤矿开采作为工程问题，通常存在对于准确性要求不高的惯性认知，但需要明确的是，危险状态的可靠判识是基于临界状态的准确描述，状态描述愈接近真实情况，所得结论的可靠性也将愈高，而随着工程条件下地面压裂、超长钻孔等大范围结构干预手段的成熟，将不再具备通过经验进行技术参数试错的空间，因此，煤岩细观结构甚至是冲击危险性的定量描述显然是具有现实意义的。
1)通过构建圆柱试样简化的弹性统计损伤物理模型，明确了变形能演化的底层物理行为，即变形能(包括弹性能)是在部分细观结构继续承载、部分细观结构断裂的过程中逐渐累积，简单用应力-应变曲线的峰前线下积分描述能量积聚、峰后线下积分描述能量耗散将造成与实际情况的不符。
2)在考虑试件中承载结构变形和破断同时发生的前提下，试件整体产生Δtu位移时，变形势能的增量ΔWti，等于该时步试件中仍具有承载能力结构中新增的变形能与该时步破断承载结构所释放的变形能之差，而由结构面摩擦、裂隙发育等造成的能量耗散将在后续工作中予以丰富，以获得更为准确的结果。
3)基于物理模型指出，项的物质载体是当前时步仍然具有承载能力的完整结构，据此进行弹性能描述更为合理，并依据实际可测的原则，给出了该指标基于荷载-时间曲线和声发射信息的计算路径。
[1] 齐庆新,彭永伟,李宏艳,等.煤岩冲击倾向性研究[J].岩石力学与工程学报,2011,30(S1):2736-2742.
QI Qingxin, PENG Yongwei, LI Hongyan.Study of bursting liability of coal and rock[J].Chinese Journal of Rock Mechanics and Engineering, 2011,30(S1):2736-2742.
[2] 潘一山,耿 琳,李忠华.煤层冲击倾向性与危险性评价指标研究[J].煤炭学报,2010,35(12):1975-1978.
PAN Yishan，GENG Lin，LI Zhonghua.Research on evaluation indices for impact tendency and danger of coal seam[J].Journal of China Coal Society，2010，35(12):1975-1978.
[3] 姜耀东,赵毅鑫,何满潮,等.冲击地压机制的细观实验研究[J].岩石力学与工程学报,2007，26(5):901-907.
JIANG Yaodong, ZHAO Yixin, HE Manchao,et al.Investigation on mechamism of coal mine bumps based on mesoscopic experiments[J].Chinese Journal of Rock Mechanics and Engineering, 2007, 26(5): 901-907.
[4] 蔡 武,窦林名,韩荣军,等.基于损伤统计本构模型的煤层冲击倾向性研究[J].煤炭学报,2011,36(S2):346-352.
CAI Wu，DOU Linming，HAN Rongjun，et al.Bursting liability of coal based ondamage statistical constitutive model[J].Journal of China Coal Society，2011，36(S2)：346-352.
[5] 齐庆新,李晓璐,赵善坤.煤矿冲击地压应力控制理论与实践[J].煤炭科学技术,2013,41(6):1-5.
QI Qingxin, LI Xiaolu, ZHAO Shankun.Theory and practices on stress control of mine pressure bumping[J].Coal Science and Technology, 2013,41(6):1-5.
[6] 刘少虹,潘俊锋,夏永学,等.基于地音与电磁波CT的掘进工作面冲击危险性层次化评价方法研究[J].煤炭学报, 2018, 43(8):2107-2116.
LIU Shaohong, PAN Junfeng, XIA Yongxue,et al.Research on the risk hierarchical assessment of rock burst of heading face based on acoustic emission and electromagnetic wave CT system[J].Journal of China Coal Society 2018, 43(8): 2107-2116.
[7] 蓝 航, 齐庆新, 潘俊锋,等.我国煤矿冲击地压特点及防治技术分析[J].煤炭科学技术, 2011, 39(1):11-15.
LAN Hang, QI Qingxin, PAN Junfeng,et al.Analysis on features as well as prevention and control technology of mine strata pressure bumping in China[J].Coal Science and Technology, 2011, 39(1):11-15.
[8] 中华人民共和国国家标准编写组.GB/T 25217.1—2010 冲击地压测定、监测与防治方法第2 部分：煤的冲击倾向性分类及指数的测定方法[S].北京：国家煤炭工业局行业管理司，2010.
[9] 李海涛，宋 力，周宏伟，等.多加载速率影响下煤强度的非线性演化机制试验研究及应用[J].岩石力学与工程学报，2016，35(S1)：2978-2989.
LI Haitao，SONG Li，ZHOU Hongwei，et al.Experimental study of nonlinear evolution mechanism of coal strengthunder multi-loading rates and its application[J].Chinese Journal of Rock Mechanics and Engineering，2016，35(S1)：2978-2989.
[10] 赵毅鑫,姜耀东,张 雨.冲击倾向性与煤体细观结构特征的相关规律[J].煤炭学报,2007，32(1):64-68.
ZHAO Yixin，JIANG Yaodong，ZHANG Yu.The correlation between the impact tendencyand the structural characteristics of coal mesostructure[J].Journal of China Coal Society，2007，32(1)：64-68.
[11] 孙中学.煤岩细观结构特征与冲击倾向性关系研究[D].阜新：辽宁工程技术大学,2016.
SUN Zhongxue.Study on the relationship between the coal rock soscopic structure characteristic and bursting liability[D].Fuxin:Liaoning Technical Vniversity,2016.
[12] 李海涛,齐庆新,赵善坤,等.煤矿动力灾害广义“三因素”机理探讨[J].煤炭科学技术,2021,49(6):42-52.
LI Haitao,QI Qingxin,ZHAO Shankun,et al.Discussion on generalized “three factors” mechanism of coal mine dy-namic disaster[J].Coal Science and Technology,2021,49(6):42-52.
[13] 黄 达, 黄润秋, 张永兴.粗晶大理岩单轴压缩力学特性 的静态加载速率效应及能量机制试验研究[J].岩石力学与工程学报, 2012, 31(2): 245-255.
HUANG Da, HUANG Runqiu, ZHANG Yongxing.Experimental investigations on static loading rate effects on mechanical properties and energy mechanism of coarse crystal grain marble under uniaxial compression[J].Chinese Journal of Rock Mechanics and Engineering, 2012, 31(2): 245-255.
[14] 李 博,叶鹏进,黄 林,等.干燥与饱和岩石裂隙受压变形与声发射特性研究[J].岩土工程学报,2021,43(12):2249-2257.
LI Bo, YE Pengjin, HUANG Lin.Deformation and acoustic emission characteristics of dry and saturated rock fractures[J].Chinese Journal of Geotechnical Engineering[J].2021,43(12):2249-2257.
[15] 鞠文君,卢志国,高富强,等.煤岩冲击倾向性研究进展及综合定量评价指标探讨[J].岩石力学与工程学报,2021,40(9):1839-1856.
JU Wenjun, LU Zhiguo, GAO Fuqiang,et al.Research progress and comprehensive quantitative evaluation index of coal rock bursting liability[J].Chinese Journal of Rock Mechanics and Engineering,2021,40(9):1839-1856.
[16] RICHARD S.Analysis of fault-slip mechanisms in hard rock mining[D].Montreal：McGill University，1999.
[17] 郭建卿，苏承东.不同煤试样冲击倾向性试验结果分析[J].煤炭学报，2009，34(7)：897-902.
GUO Jianqing，SU Chengdong.Analysis on experimental results of rock burst tendency of different coal samples[J].Journal of China Coal Society，2009，34(7)：897-902.
[18] SINGH S P.Burst energy release index[J].Rock Mechanics and Rock Engineering，1988，21(2)：149-155.
[19] 
A.Bursting liability indices of coal[J].Interna-tional Journal of Rock Mechanics and Mining Science and Geomechanics Abstracts，1981，18(4)：295-304.
[20] 唐礼忠，潘长良，王文星.用于分析岩爆倾向性的剩余能量指数[J].中南工业大学学报：自然科学版，2002，33(2)：129-132.
TANG Lizhong，PAN Changliang，WANG Wenxing.Surplus energy index for analysing rock burst proneness[J].Chinese Journal of Rock Mechanics and Engineering，2002，33(2)：129-132.
[21] 宫凤强，闫景一，李夕兵.基于线性储能规律和剩余弹性能指数的岩爆倾向性判据[J].岩石力学与工程学报，2018，37(9)：1993-2014.
GONG Fengqiang，YAN Jingyi，LI Xibing.A new criterion of rock burst proneness based on the linear energy storage law and the residual elastic energy index[J].Chinese Journal of Rock Mechanics and Engineering，2018，37(9)：1993-2014.
[22] 卢志国，鞠文君，高富强，等.基于非线性储能与释放特征的煤冲击倾向性指标[J].岩石力学与工程学报，2021，40(8)：1559-1569.
LU Zhiguo，JU Wenjun，GAO Fuqiang，et al.Bursting liability index of coal based on nonlinear storage and release characteristics of elastic energy[J].Chinese Journal of Rock Mechanics and Engineering，2021，40(8)：1559-1569.