0 引 言
随着能源需求加剧,矿山开采水平逐渐加深。通常情况下,硬脆性岩石在深地条件下易发生动力灾害,软岩常发生挤压大变形,这些破坏特征与岩性(脆性/延性)直接相关。在煤矿中,煤岩脆性破坏时常释放大量能量,在采掘中表现为冲击地压[1-2]。评估有冲击倾向性且评价有冲击危险性的新建矿井,以及冲击地压矿井新水平、新煤层,应当进行煤岩冲击倾向性鉴定,通过冲击倾向性指标评价煤岩脆性破坏特征。另一方面,煤岩在高应力水平时发生脆延转换,软弱围岩的延性特征突出,引起巷道两帮挤压和底鼓,危害矿山安全。因此,脆/延性描述和冲击倾向性评价研究对深部矿山安全性分析和灾害防治具有重要意义[3-5]。
为表征岩石的脆性破坏特征,研究者们基于不同角度提出了众多的脆性指标和冲击倾向性指标[6-26]。其中,基于强度、内摩擦角或弹性参数建立的指标反映了强度或变形与冲击倾向性的关系,没有考虑应变能转化;基于硬度建立的指标反映了不同矿物成分对总体表观硬度的影响,无法反映应力状态的依赖性;全应力-应变曲线记录了岩石从开始承受荷载到最后失去承载力的全过程,既能表达岩石在荷载作用下的应力-应变关系,也可以反映能量演化规律。
因此,从应力-应变曲线角度建立表征煤岩不同破坏程度的指标具有可行性。通过总结现有的脆性和冲击倾向性指标,基于全应力-应变曲线提出了一种新型的表达煤岩不同破坏特征的统一脆延性指标,建立了不同破坏等级判定标准,并结合室内试验进行了分析与探讨。相对于传统指标,提出的指标进行了无量纲化表达,可以同时量化岩石的脆性和延性变形特征与破坏程度;通过采用指数运算,对峰后跌落的微小差别进行了放大,能够突出不同煤岩单轴条件下脆性跌落的差别;另一方面,脆延转换伴随岩体应力状态调整,是深部岩体采掘活动中必然存在的现象,提出的指标普遍适用于煤岩在多轴和不同应力状态下的脆性或延性破坏程度表征,在深部采掘活动灾变分析与防治中具有推广潜力。
1 基于应力-应变曲线的冲击倾向性指标
表1汇总了部分脆性指标和冲击倾向性指标(B1~B29为表征煤岩脆性破坏程度的脆性指标或冲击倾向性指标),其中从应力-应变曲线角度建立的指标可充分表征煤岩不同破坏程度和能量演化规律。

续表

分类依据指标及表达式参数说明内摩擦角B12=sin φ[7]B13=45°+φ2[7]φ为内摩擦角(当σn=0时);σn为破坏面上的法向应力应力-应变曲线峰前B14=σp/εp[14]B15=εe/εp[7]B16=(U1+U2)/U1[15]B17=U1/U2[6]B18=σc2/2E[16]σp为峰值强度;εp为峰值应变;εe为峰前可恢复应变;U1为弹性应变能;U2为峰前耗散能峰后B19=(σp-σr)/σp[17]B20=(εr-εp)/εp[18]B21=(σp-σr)σplg|kac|10[19]σr为残余强度;εr为残余应变;kac为峰后应力降斜率其他B22=(U1+U2)/(U3+U4)[6]B23=σP-σrσPsin φ·eE10×M[20]B24=εp(σp-σr)/σp/(εr-εp)[21]B25=U1-(U3+U4)[22]B26=U1/(U3+U4)[23]B27=(σp-σci)/εpσp(εp-εci)+(σp-σr)/εpσp(εr-εp)[24]B28=[1-e-σp-σci10εp(εp-εci)][1-eσp-σr10εp(εp-εr)][25]B29=U1+U4U1+U2+U3+U4U1+U4U1-U3U2U1-U3[26]U3为残余弹性能;U4为峰后外力对岩石的机械功增量;M为峰后模量;σci为起裂应力;εci为起裂应变
1.1 基于峰前曲线的冲击倾向性指标
B14和B15仅反映了峰值特征,如图1所示,2种岩石的峰值强度与峰值应变的比值相等,则B14相同;峰前弹性应变与峰值应变相等,则B15相同。但是,2种岩石的峰后应力降特征不同,采用B14和B15无法反映图1中2种岩石不同的峰后跌落。
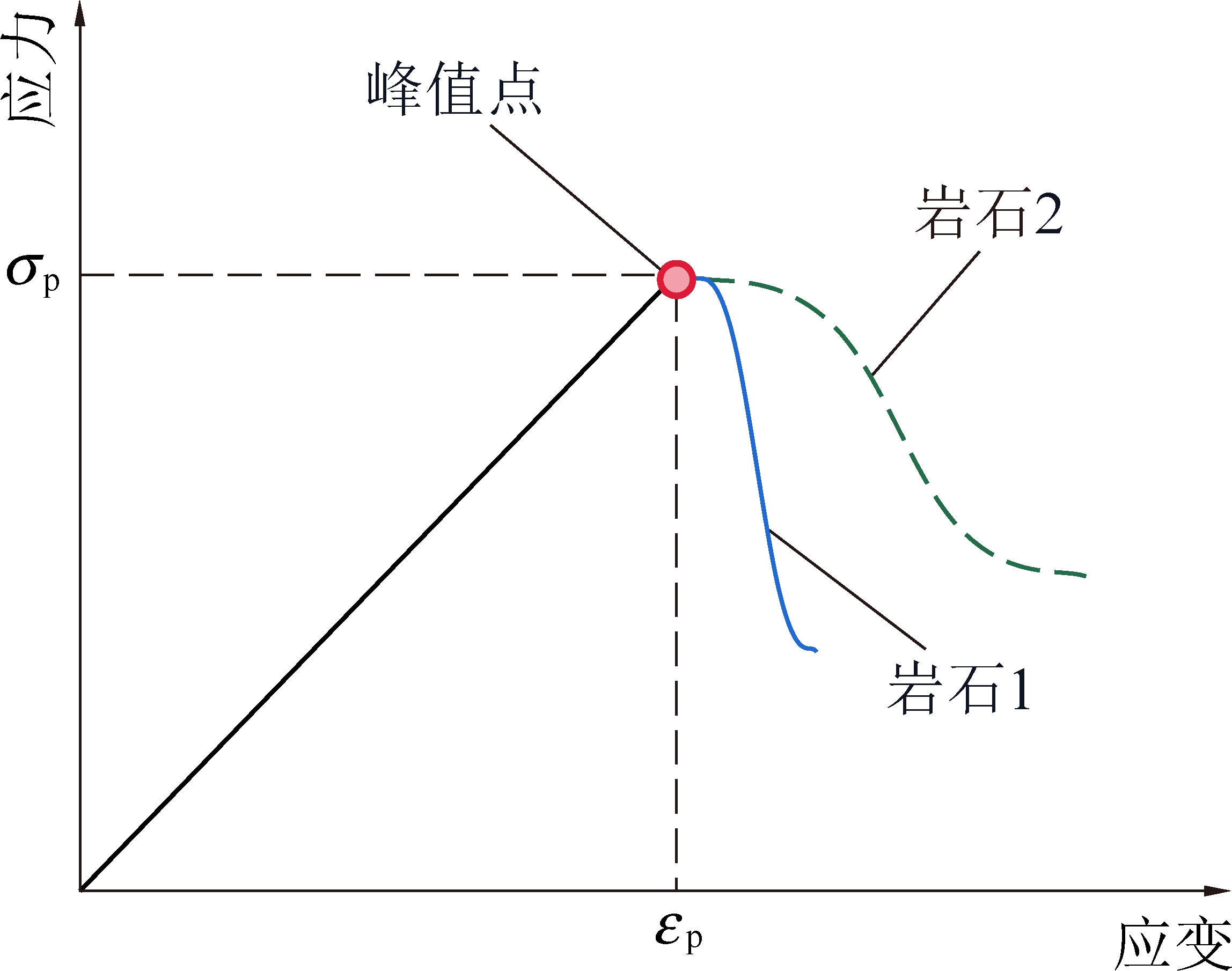
图1 B14和B15无法合理量化冲击倾向性的情况
Fig.1 B14 and B15 can not reasonably quantify burst tendency
B16、B17和B18均是基于峰前应变能演化的角度提出的。如图2所示,在峰前阶段,外力对岩石做的功转化为弹性应变能U1和耗散能U2。普遍认为岩石破坏时释放的能量由峰前弹性应变能提供,峰前弹性应变能占比越高,同时破坏过程中所需的外力对岩石的机械功增量U4越少,冲击倾向性越大。但是,B16、B17和B18仅分析了峰前的应变能演化规律,忽略了峰后特征。
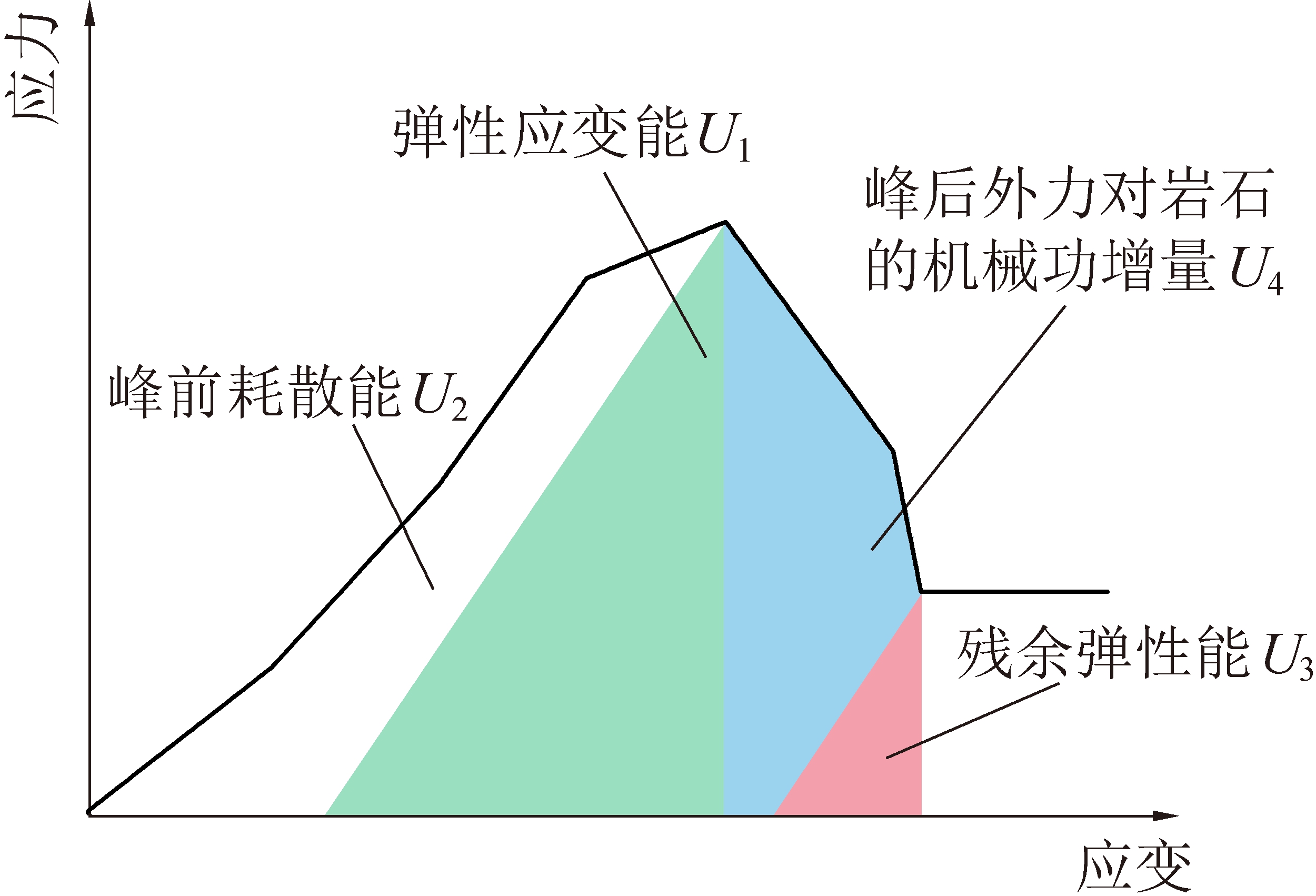
图2 基于全应力-应变曲线的应变能演化示意
Fig.2 Schematic of strain energy evolution analysis based on total stress-strain curve
1.2 基于峰后曲线的冲击倾向性指标
B19采用峰后应力降与峰值强度的比值,如图3所示,2种岩石峰后应力降与峰值强度相等,B19相等,但岩石1的峰后跌落更剧烈,冲击倾向性更大。
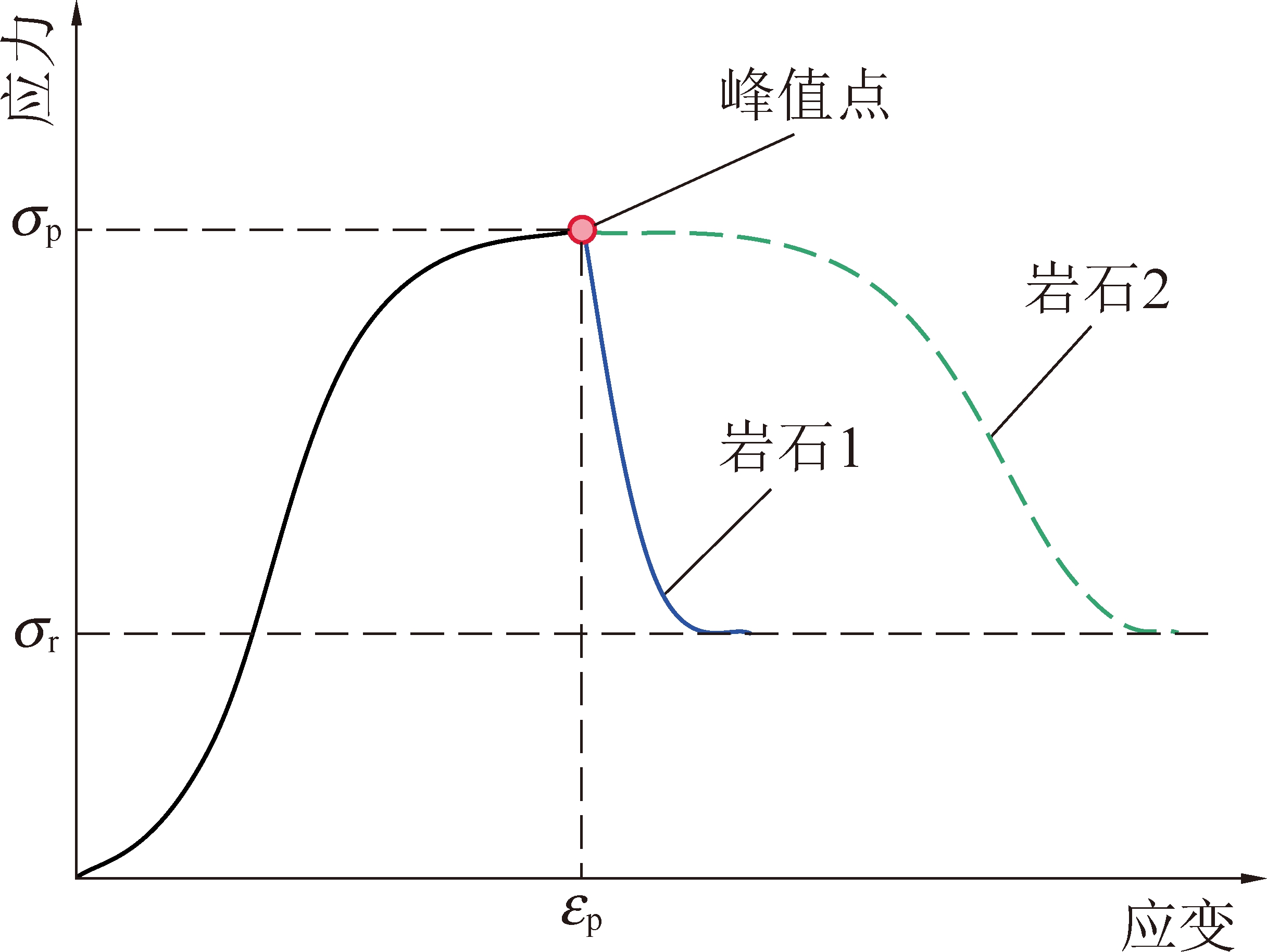
图3 B19无法合理量化冲击倾向性的情况
Fig.3 B19 can not reasonably quantify burst tendency
B20采用峰后应变差与峰值应变的比值,如图4所示(σr1为岩石1的残余强度,σr2为岩石2的残余强度),2种岩石峰后应变差与峰值应变相等,B20相等,但岩石1的峰后跌落更剧烈,冲击倾向性更大。
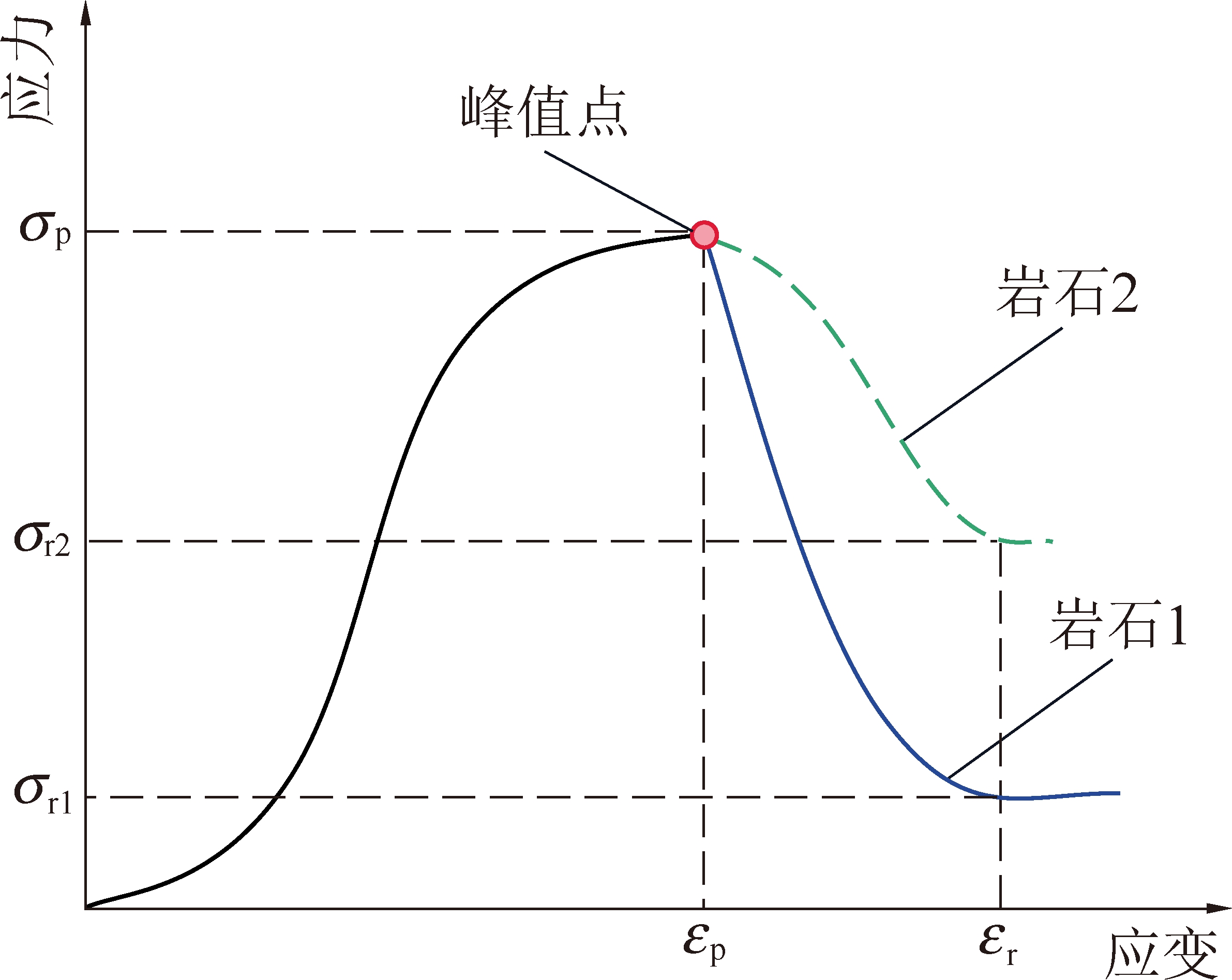
图4 B20无法合理量化冲击倾向性的情况
Fig.4 B20 can not reasonably quantify burst tendency
B21考虑了峰后曲线的应力降、斜率和峰值强度,但是,该指标忽略了峰前特性。如图5所示,2种岩石的峰后应力降、峰后斜率、峰值强度均相等,由于峰前弹性模量的差异,岩石2在峰前储存的弹性应变能更多,导致峰后释放应变能占峰前储存弹性能的比例更大,岩石2的冲击倾向性比岩石1大。
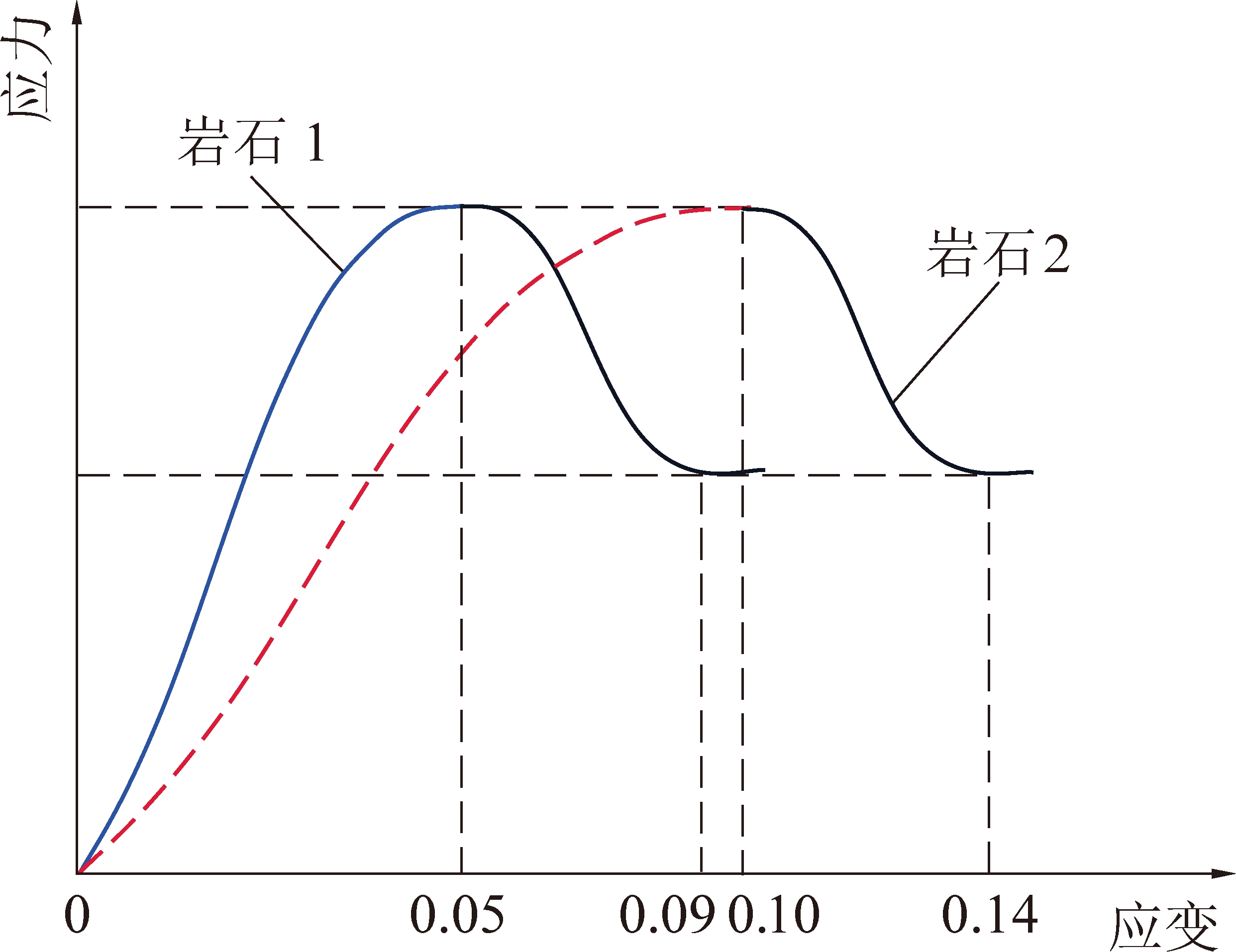
图5 B21无法合理量化冲击倾向性的情况
Fig.5 B21 can not reasonably quantify burst tendency
2 统一脆延性指标的建立
由前述分析可见,为科学量化深部煤岩动力灾变难易程度,需基于全应力-应变曲线建立冲击倾向性指标,同时考虑峰前和峰后特征,反映峰前弹性能积累和峰后应变能释放速率和程度:①峰前弹性模量越小,强度越大,峰前应变能积累值越大,可供释放应变能越多,冲击倾向性越高;②峰后模量越大,峰值强度越高,峰后应力下降越大,峰后应变能释放量值和速率越大,应变能释放率(应变能释放值/应变能积累值)越大,冲击倾向性越高。
因此,在建立脆性和冲击倾向性指标时,应合理考虑全应力-应变曲线峰前和峰后特征。另外,为反映高应力水平时延性破坏特征,可在冲击倾向性指标基础上将其扩展到延性评价,进一步扩大指标对岩性评价适用范围。
为此,建立统一脆延性指标,表达式如下:
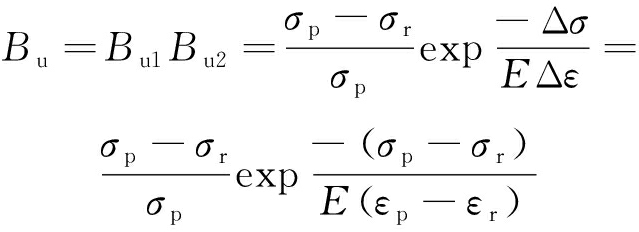
(1)
式中:E为峰前弹性模量;σp为峰值强度;σr为残余强度;εp为峰值应变;εr为残余应变;Δε为峰后应变变化值;Δσ为峰后与Δε对应的应力变化值;Δσ/Δε=(σp-σr)/(εp-εr)。Bu1和Bu2分别为统一脆延性指标的子指标,表达式分别为
(2)
(3)
为说明岩性对各指标的影响,采用图6的峰后具有不同特征的全应力-应变曲线进行分析。

图6 峰后不同变形特征的全应力-应变曲线
Fig.6 Total stress-strain curves with different deformation characteristics after peak
在Bu1表达式中,分子采用峰值点到残余点的应力变化量,反映峰后应力变化程度,分母采用峰值强度,可以消除量纲。对于不同岩性,Bu1分以下4种情况讨论:
1)对于峰后应变软化的脆性岩石,分子为正值,且分子与分母比值越大,峰后应力降低比例越大,残余强度比峰值强度越小,峰后释放弹性能越多,冲击倾向性越强。
2)理想脆性岩石σr=0,Bu1数值为1。
3)对于峰后应变硬化、具有延性特征的岩石,Bu1表达式中分子为负值,且分子数值越小,峰值强度和残余强度的差值越大,峰后应变硬化特点越明显。
4)当岩石为理想弹塑性岩石时,峰值强度与残余强度相等,Bu1数值为0。
因此,Bu1的正负取值指示了不同岩性,Bu1<0时为应变硬化,Bu1>0时为应变软化;同时,Bu1的数值大小表达了峰后应变强化或软化的程度。
Bu2表达式采用了对峰后模量与峰前弹性模量比值的指数运算形式,且无量纲。对于不同岩性,Bu2分以下4种情况讨论:
1)对于峰后应变软化的脆性岩石,-Δσ/(EΔε)为正值。峰后模量越大,弹性模量越小,表明峰前积累的弹性应变能越多,同时积累的弹性应变能在峰后释放比例也越大。因此,-Δσ/(EΔε)数值越大,Bu2越大,则冲击倾向性越强。
2)当岩石为理想脆性时,应变差εr-εp趋于0+,(σr-σp)/(εr-εp)趋于-∞,-Δσ/(EΔε)趋于+∞,其指数函数Bu2也趋于+∞。
3)对于峰后应变硬化、具有延性特征的岩石,-Δσ/(EΔε)为负值。峰后模量越大,弹性模量越小,表明全过程积累弹性应变能的能力越强,-Δσ/(EΔε)为负且数值越小,Bu2越小,峰后应变硬化特点越明显。
4)当岩石为理想弹塑性岩石时,-Δσ/(EΔε)数值为0,Bu2数值为1。
如图7所示,-Δσ/(EΔε)的正负或Bu2与1的关系指示了不同岩性,-Δσ/(EΔε)或Bu2>1时为应变软化,-Δσ/(EΔε)或Bu2<1时为应变硬化;Bu2的数值大小表达了峰后应变强化或软化的程度。
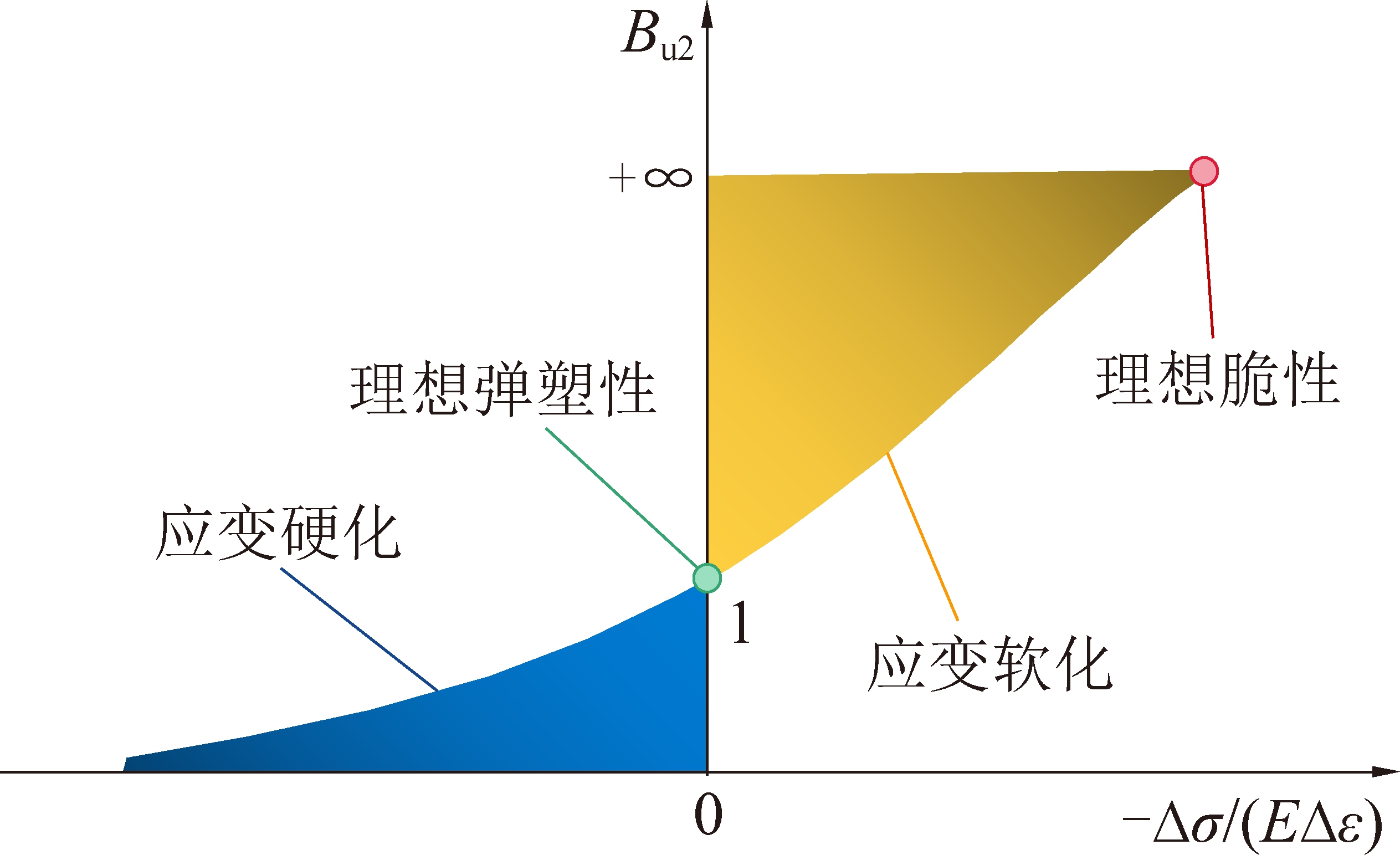
图7 Bu2与-Δσ/(EΔε)的演化关系
Fig.7 Evolution relationship between -Δσ/(EΔε) and Bu2
综合以上分析,汇总了Bu1、Bu2和Bu与不同变形特征的对应关系(表2)。
表2 Bu1、Bu2和Bu与不同变形特征的对应关系
Table 2 Correspondence between Bu1, Bu2, Bu and different deformation characteristics

变形特征峰后应变硬化理想弹塑性峰后应变软化理想脆性Bu1Bu1<0Bu1=00
3 统一脆延性指标的验证
3.1 单轴条件下不同煤岩评价
为验证建立的统一脆延性指标Bu,选用了单轴下5种煤岩[27-29]试验数据进行分析。图8为煤岩在单轴下的应力-应变曲线,煤岩1的应力达到峰值强度后跌落,峰前应变能在峰后基本全部释放,脆性破坏特征最强;煤岩2峰后比煤岩1稍缓,脆性比煤岩1弱;煤岩3峰后与煤岩2相似,但应力跌落数值比煤岩2小;煤岩4峰后比煤岩3更缓;煤岩5峰值强度和弹性模量最小,峰前积累的应变能最低,峰后跌落较缓,脆性破坏特征最弱。从定性角度分析煤岩脆性大小关系:煤岩1>煤岩2>煤岩3>煤岩4>煤岩5。
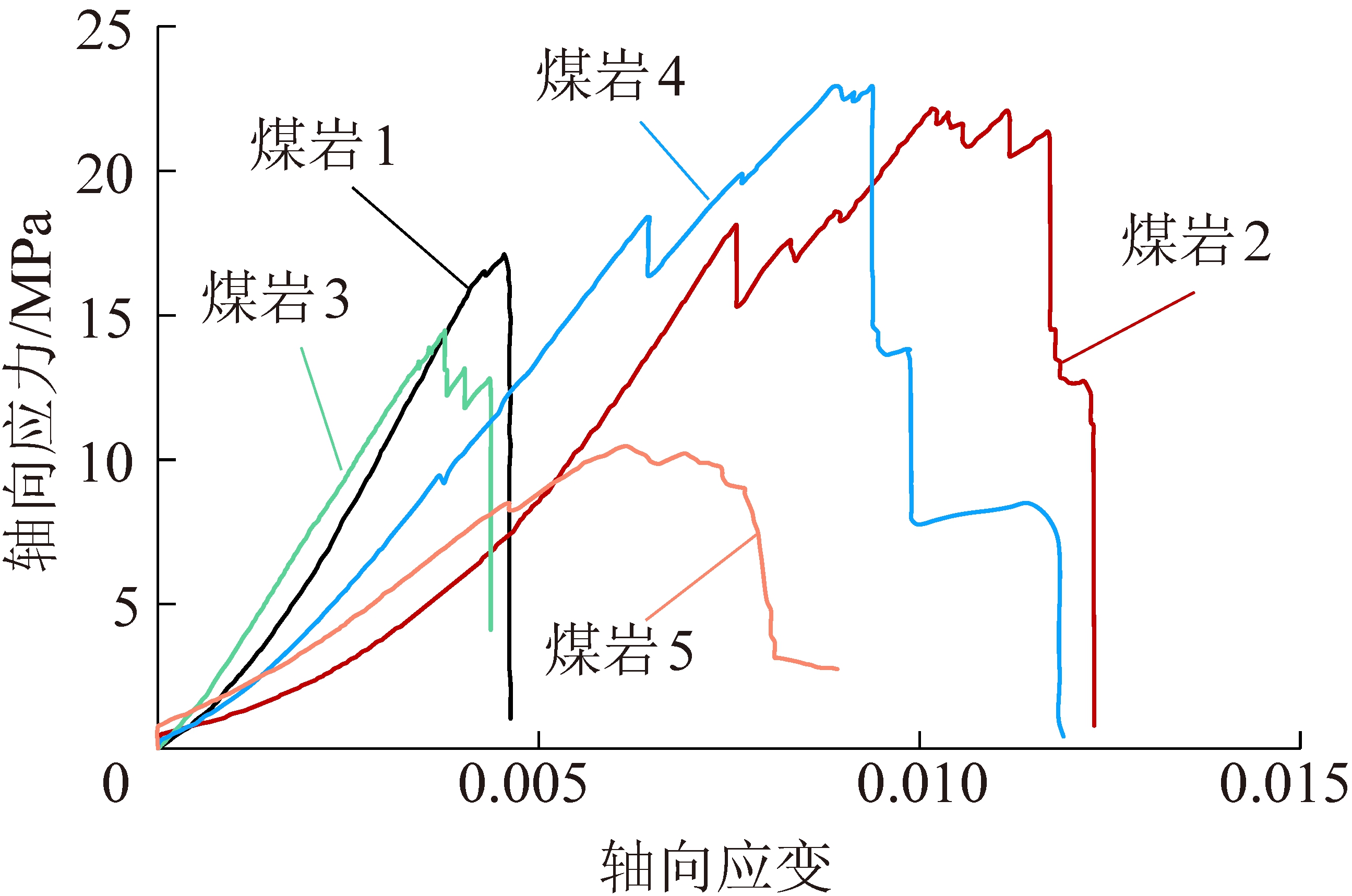
图8 5种煤岩在单轴下的应力-应变曲线
Fig.8 Stress-strain curves of 5 coal rocks under uniaxial test
选取B17,B18,B19及B22四种指标与本文的统一脆延性指标Bu进行计算,煤岩基本力学参数见表3。
表3 煤岩单轴压缩数据与脆性破坏表征指标
Table 3 Uniaxial compression test data of coals and brittleness index
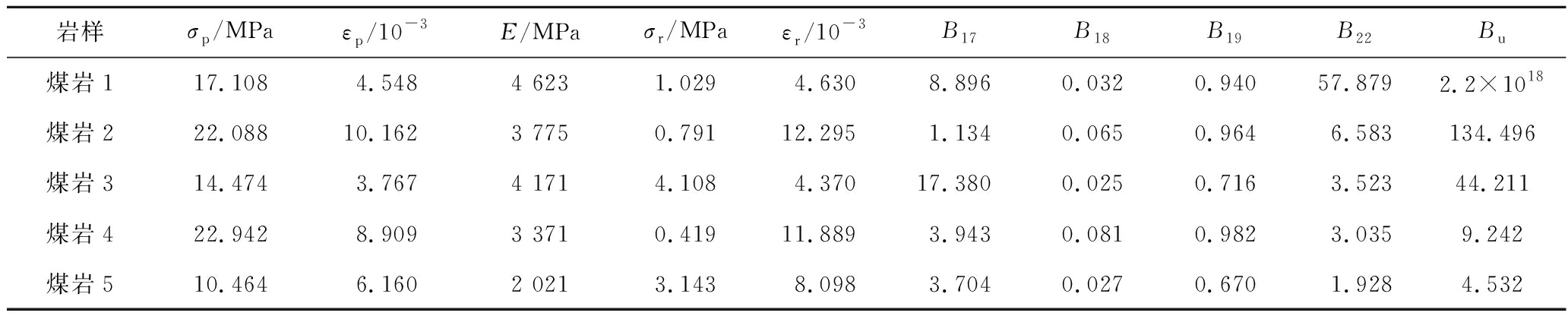
岩样σp/MPaεp/10-3E/MPaσr/MPaεr/10-3B17B18B19B22Bu煤岩117.1084.5484 6231.0294.6308.8960.0320.94057.8792.2×1018煤岩222.08810.1623 7750.79112.2951.1340.0650.9646.583134.496煤岩314.4743.7674 1714.1084.37017.3800.0250.7163.52344.211煤岩422.9428.9093 3710.41911.8893.9430.0810.9823.0359.242煤岩510.4646.1602 0213.1438.0983.7040.0270.6701.9284.532
图9为单轴条件下煤岩的脆性破坏程度评价,可见,B17、B18、B19与其他指标相比结果不具有一致性,从前文分析可知,B17、B18、B19均为基于峰前或峰后曲线提出的指标,不能完全表达脆性破坏特征。B22为煤炭领域国家标准中采用的冲击倾向性指标[6],B22与Bu评价结果和定性分析一致,验证了笔者提出的指标。
值得注意的是,由于单轴压缩下峰后急剧跌落,传统的指标计算得到的冲击倾向性结果差别不大,脆性破坏特征区分不明显,如图9所示。提出的指标在数学形式上采用了指数函数,对急剧跌落特征的差别进行了放大,指标计算结果差别明显。
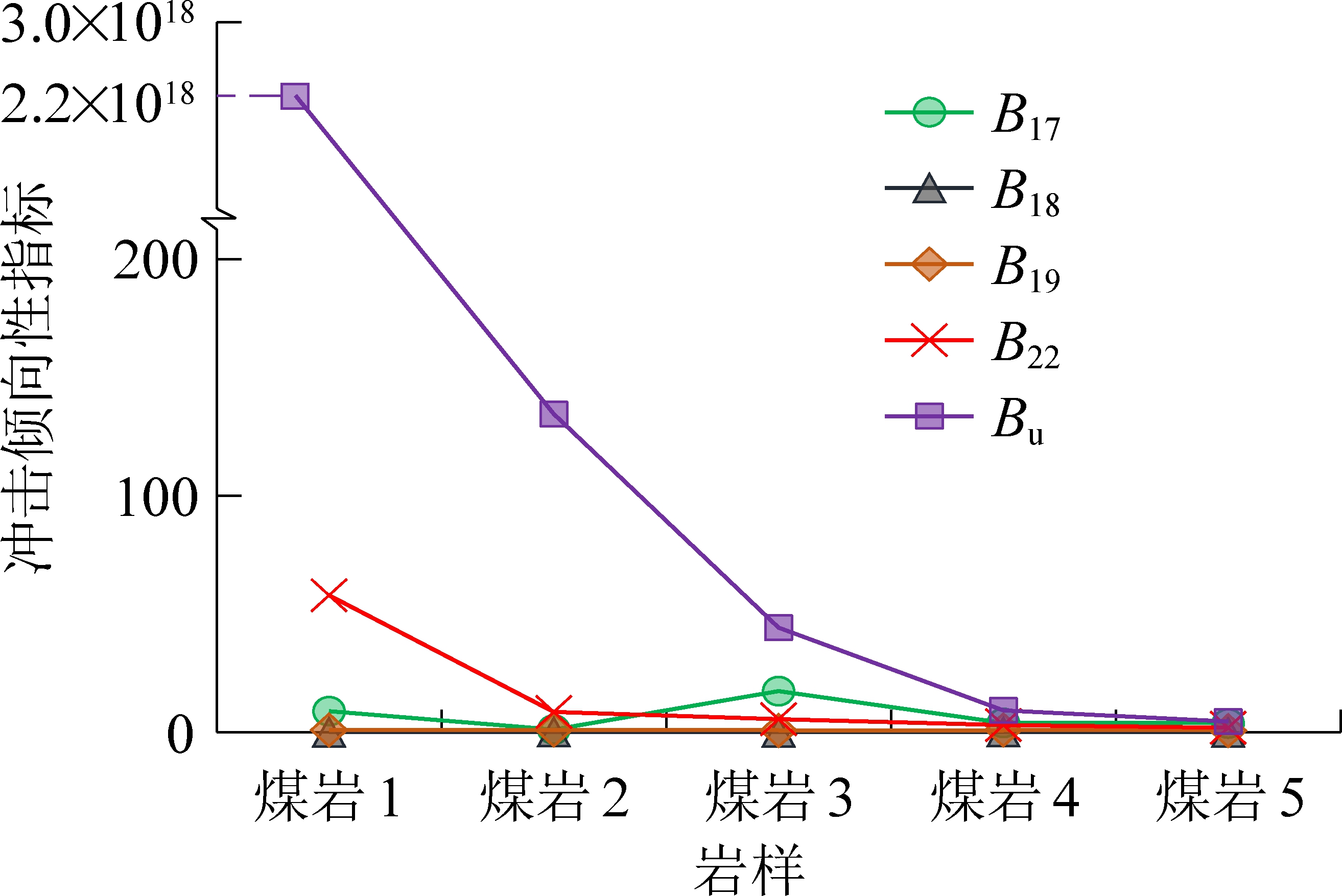
图9 单轴条件下5种煤岩的脆性破坏程度表征
Fig.9 Brittleness index of five coals under uniaxial condition
3.2 同种岩石不同围压下的评价
图10为白云岩在不同围压下的全应力-应变曲线[30](图中虚线连接了峰值点和残余点,可以直观反映峰后模量)。可见,白云岩的脆延转换特征较为明显,围压低于40 MPa时,峰后呈应变软化趋势;当围压大于40 MPa时,峰后呈应变硬化特征。
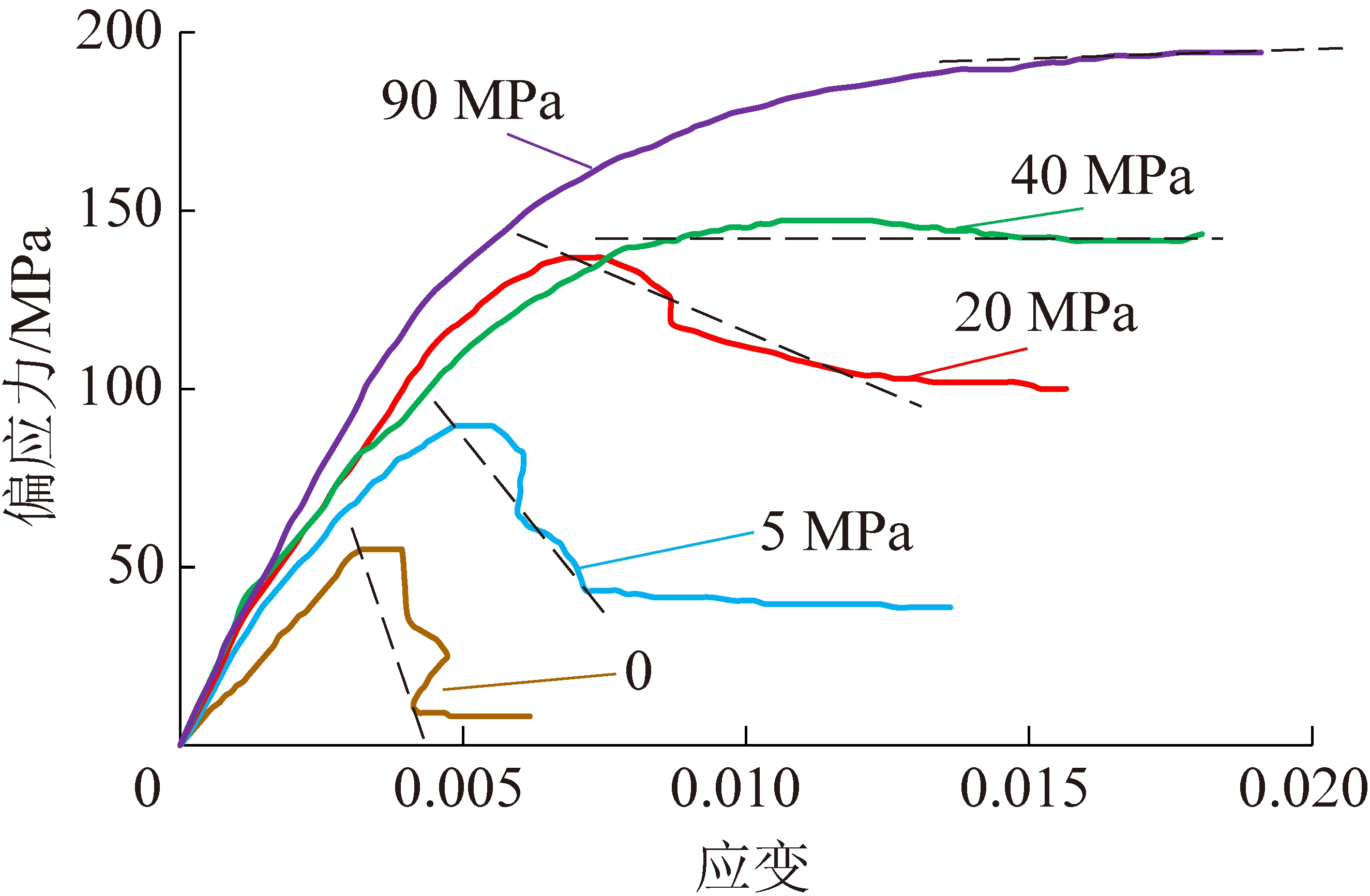
图10 不同围压下白云岩的应力-应变曲线
Fig.10 Stress-strain curves of dolomite under different confining pressures
目前的冲击倾向性指标或脆性指标的适用范围大多局限于硬脆性描述,无法反映白云岩围压大于等于40 MPa的情况。
采用统一脆延性指标计算不同围压下的白云岩的破坏特征(图11),可见,在0~40 MPa,岩石由应变软化向理想弹塑性转变,Bu随着围压的升高而递减,脆性破坏程度减弱;当围压达到40 MPa时,Bu数值约为0,可认为围压在40 MPa下的白云岩为理想弹塑性变形;对围压90 MPa,峰后表现为硬化特征,Bu数值为负值。因此,统一脆延性指标不仅可以反映白云岩在中低围压下的脆性破坏程度,还可以适用于高围压的延性特征表达。
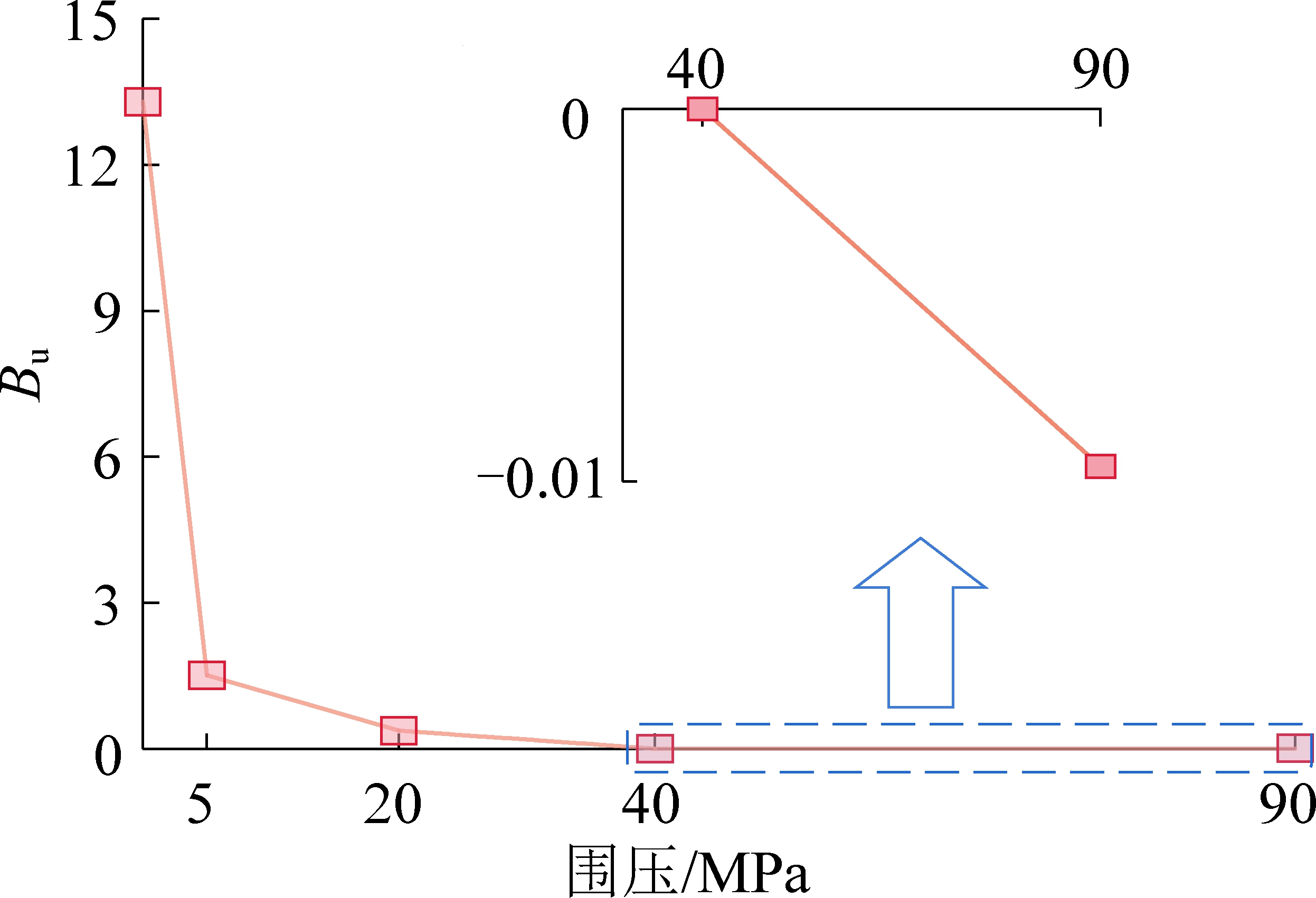
图11 白云岩的冲击倾向性随围压的变化规律
Fig.11 Variation law of burst tendency of dolomite with confining pressure
4 统一脆延性指标与冲击倾向性指标的思考
煤岩的冲击倾向性指的只是煤岩本身的材料属性,即这种煤岩本身是否容易发生冲击现象,与实际工程中煤岩所处的应力状态等外界条件无关。相应地,国家标准中对于煤的冲击倾向性计算采用了单轴压缩试验,可以评价不同种类煤岩的冲击倾向性,对有冲击倾向性的煤层必须进行冲击危险性评价,冲击地压危险区域应进行防冲设计。
脆性指标表达的是岩石或煤的脆性破坏程度,常用于评价水力压裂效果、破岩效率、岩爆/冲击地压倾向性等。脆性指标的概念更为宽泛,与具体行业应用相结合,计算中可评价不同应力状态下脆性破坏特征。当采用单轴试验时,脆性指标与冲击倾向性指标意义相近。
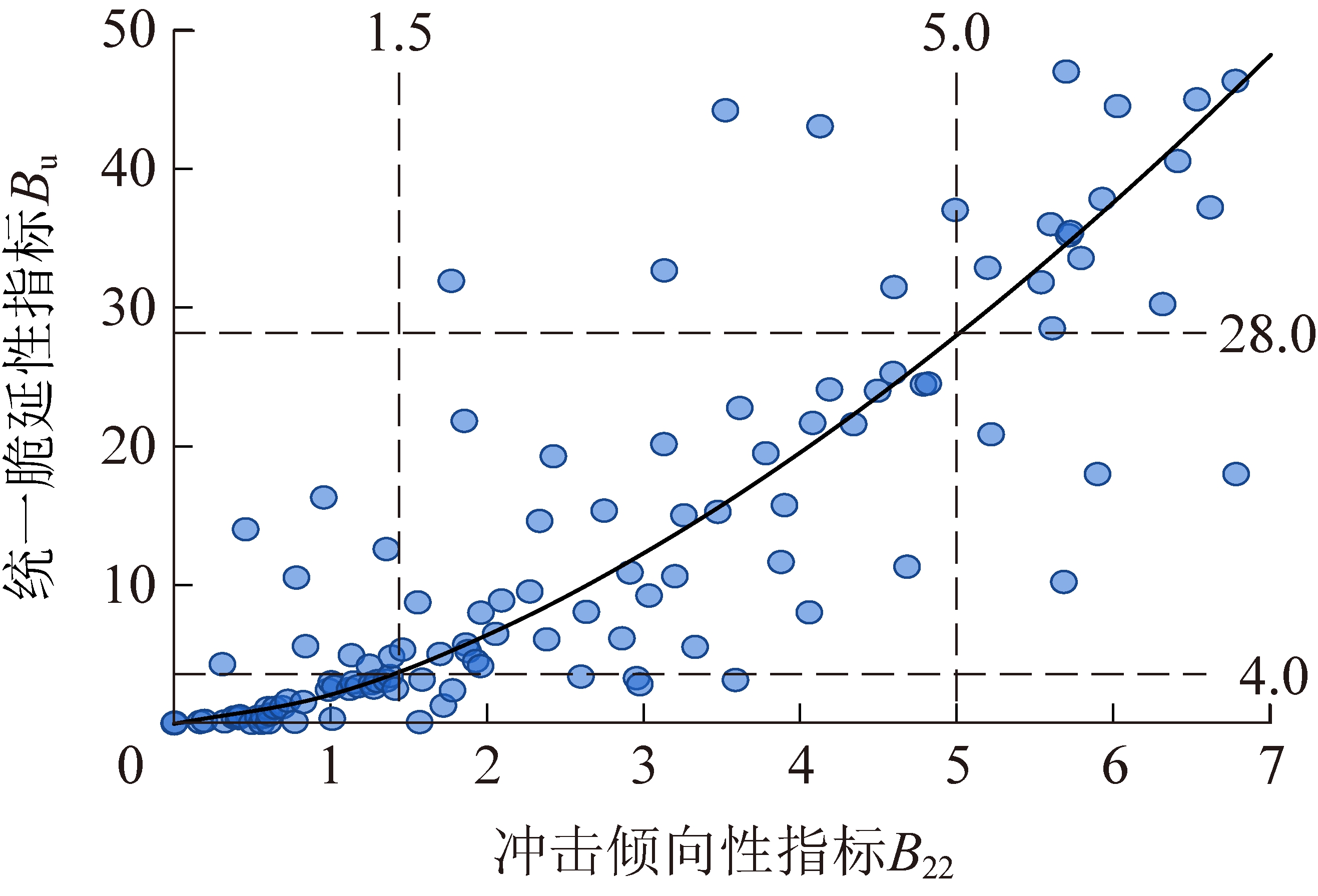
图12 B22和Bu的拟合曲线
Fig.12 Fitting curve of B22 and Bu
国家标准[6]中基于冲击倾向性指标B22提出的分类标准具有较好的适用性,通过汇总整理大量试验数据,分别通过冲击倾向性指标B22和统一脆延性指标Bu计算其冲击倾向性,剔除了一些差异较大的数据,采用曲线拟合的方法,进而实现基于统一脆延性指标Bu的冲击倾向性等级划分。
图12所示的拟合曲线反映了冲击倾向性指标B22和统一脆延性指标Bu之间的关系,拟合曲线的函数表达式为:
Bu=2.094B221.611
(4)
以B22分类标准为基础,依据式(4),可得到基于统一脆延性指标Bu的冲击倾向性分类标准(表4)。
表4 B22和Bu的分类标准
Table 4 Classification criteria of B22 and Bu
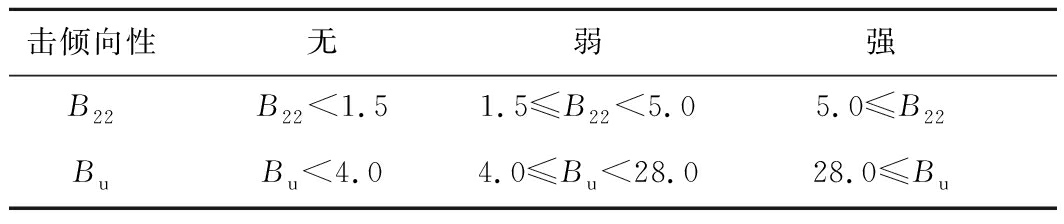
击倾向性无弱强B22B22<1.51.5≤B22<5.05.0≤B22BuBu<4.04.0≤Bu<28.028.0≤Bu
值得注意的是,在深部矿山采掘活动中,围岩内部在扰动下损伤贯通,或断层活化导致的弹射、抛射诱冲现象较为广泛,该情况下煤岩破裂处应力状态并非单纯的单轴或双轴应力条件。应力状态的不一致性可能导致目前的冲击倾向性鉴定结论与是否冲击不直接相关,例如评价有冲击倾向性的煤层不发生冲击危险。为此,在目前的防冲体系中,冲击倾向性鉴定后,对于有冲击倾向性煤层进行冲击危险性区域划分,进一步人为地划定为无冲击危险性区域、弱冲击危险区域、中等冲击危险性区域和强冲击危险性区域。然而,在冲击危险性区域划定和防冲设计时常具有主观性,有必要采用类似本文提出的指标定量评价多轴条件下围岩破坏特征,例如将指标嵌入数值程序评估卸压范围等。因此,提出的统一脆延性指标在深部采掘活动灾变分析与防治中具有推广潜力。
综合以上分析,统一脆延性指标具有以下特点:
1)该指标通过2个子指标的结合,可以合理量化岩石变形特征(硬化/软化)与破坏程度。子指标Bu1表达了峰后应力变化量的相对程度,子指标Bu2表达了峰前和峰后应力变化速率,反映了应力-应变响应。统一脆延性指标不仅能够精准地描述硬脆性煤岩冲击倾向性,而且反映软岩或高围压岩石的峰后应变硬化特征。
2)统一脆延性指标表达式在建立过程中消除了量纲,可以适用于不同尺度的煤岩脆性破坏或延性破坏的描述。
3)采用普通试验机测试煤岩单轴压缩时,在峰后经常得到急剧的应力跌落,采用传统的冲击倾向性指标无法反映峰后跌落的微小差别,而统一脆延性指标由于采用了指数运算,对微小差别进行了放大(图9),能够突出不同煤岩单轴条件下脆性跌落的差别,对于目前规范中采用单轴压缩测试冲击倾向性具有非常好的适用性。
5 结 论
1)统一脆延性指标合理考虑了全应力-应变曲线峰前和峰后特征,采用峰前弹性模量、峰值强度、峰后模量和应力变化反映了峰前弹性应变能积累和峰后弹性应变能释放特征。
2)统一脆延性指标可以反映岩石变形特征与破坏程度,统一脆延性指标Bu<0对应峰后应变硬化,Bu=0对应理想弹塑性变形,Bu>0对应峰后应变软化,Bu趋于正无穷对应理想脆性破坏。
3)基于统一脆延性指标的冲击倾向性分为3个等级,Bu<4.0时为无冲击倾向性,Bu介于4.0与28.0之间时为弱冲击倾向性,Bu>28.0时为强冲击倾向性。
4)统一脆延性指标为无量纲指标,可以反映单轴条件和不同应力水平下脆性破坏特征,以及软弱岩石或高应力水平下岩石峰后应变硬化特征,尤其突出了单轴条件下不同煤岩脆性跌落的差别,适用性相对传统指标更为广泛。
[1] 周 辉, 张 凯, 冯夏庭, 等. 脆性大理岩弹塑性耦合力学模型研究[J]. 岩石力学与工程学报, 2010,29(12):2398-2409.
ZHOU Hui, ZHANG Kai, FENG Xiating, et al. Research on elastoplastic coupling mechanics model of brittle marble[J]. Chinese Journal of Rock Mechanics and Engineering, 2010,29(12):2398-2409.
[2] 陈国庆, 吴家尘, 蒋万增, 等. 基于弹性能演化全过程的岩石脆性评价方法[J]. 岩石力学与工程学报, 2020,39(5):901-911.
CHEN Guoqing, WU Jiachen, JIANG Wanzeng, et al. Evaluation method of rock brittleness based on the whole process of elastic energy evolution[J]. Chinese Journal of Rock Mechanics and Engineering, 2020,39(5):901-911.
[3] 杨 磊, 王晓卿, 李建忠. 不同冲击倾向性煤单轴压缩下能量演化与损伤特征[J]. 煤炭科学技术, 2021,49(6):111-118.
YANG Lei, WANG Xiaoqing, LI Jianzhong. Energy evolution and damage characteristics of coal with different shock tendencies under uniaxial compression[J]. Coal Science and Technology, 2021,49(6):111-118.
[4] 齐庆新, 李海涛, 郑伟钰, 等. 煤岩弹性变形能的表征物理模型及实测方法[J]. 煤炭科学技术, 2022,50(1):70-77.
QI Qingxin, LI Haitao, ZHENG Weiyu, et al. Physical model and measurement method for the characterization of elastic deformation energy of coal and rock[J]. Coal Science and Technology, 2022,50(1):70-77.
[5] 郭海峰, 宋大钊, 何学秋, 等. 冲击倾向性煤不同损伤程度声发射分形特征研究[J]. 煤炭科学技术, 2021,49(9):38-46.
GUO Haifeng, SONG Dazhao, HE Xueqiu, et al. Research on the fractal characteristics of acoustic emission of shock-prone coal with different damage degrees[J]. Coal Science and Technology, 2021,49(9):38-46.
[6] GB/T 25217.2-2010, 冲击地压测定、监测与防治方法第2部分:煤的冲击倾向性分类及指数的测定方法[S].
[7] HUCKA V, DAS B. Brittleness determination of rocks by different methods[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1974, 11(10):389-392.
[8] ALTINDAG R. Correlation of specific energy with rock brittleness concepts on rock cutting[J]. Journal of the Southern African Institute of Mining and Metallurgy, 2003, 103(3):163-171.
[9] RICKMAN R, MULLEN M, PETRE E, et al. A practical use of shale petrophysics for stimulation design optimization:All shale plays are not clones of the Barnett Shale[C]. SPE Annual Technical Conference and Exhibition. OnePetro, 2008.
[10] 刘致水,孙赞东.新型脆性因子及其在泥页岩储集层预测中的应用[J].石油勘探与开发,2015,42(1):117-124.
LIU Zhishui, SUN Zandong. New brittleness factor and its application in shale reservoir prediction[J]. Petroleum Exploration and Development, 2015,42(1):117-124.
[11] LAWN B R, HARDNESS M D B. Hardness, Toughness, and brittleness:an indentation analysis[J]. Journal of the American Ceramic Society, 1979,62(7).:347-350.
[12] QUINN J B, QUINN G D. Indentation brittleness of ceramics:a fresh approach[J]. Journal of Materials Science, 1997,32(16):4331-4346.
[13] HONDA H, SANADA Y. Hardness of coal[J]. Fuel, 1956,35(4):451-461.
[14] LIANG L, LIU X, XIONG J, et al. New model to evaluate the brittleness in shale formation[C]//International Geophysical Conference, Qingdao, China, 17-20 April 2017. Society of Exploration Geophysicists and Chinese Petroleum Society, 2017:1248-1251.
[15] 张传庆, 卢景景, 陈 珺, 等. 岩爆倾向性指标及其相互关系探讨[J]. 岩土力学, 2017,38(5):1397-1404.
ZHANG Chuanqing, LU Jingjing, CHEN Jun, et al. Discussion on rockburst propensity indicators and their relationship[J]. Rock and Soil Mechanics, 2017,38(5):1397-1404.
[16] WANG J A, PARK H D. Comprehensive prediction of rockburst based on analysis of strain energy in rocks[J]. Tunnelling and Underground Space Technology, 2001, 16(1):49-57.
[17] BISHOP A W. Progressive failure-with special reference to the mechanism causing it[C]//Proc Geotech Conf Oslo,1967, 2:142-150.
[18] HAJIABDOLMAJID V, KAISER P. Brittleness of rock and stability assessment in hard rock tunneling[J]. Tunnelling and Underground Space Technology, 2003,18(1):35-48.
[19] 周 辉, 孟凡震, 张传庆, 等. 基于应力-应变曲线的岩石脆性特征定量评价方法[J]. 岩石力学与工程学报, 2014,33(6):1114-1122.
ZHOU Hui, MENG Fanzhen, ZHANG Chuanqing, et al. Quantitative evaluation method of rock brittleness characteristics based on stress-strain curve[J]. Chinese Journal of Rock Mechanics and Engineering, 2014,33(6):1114-1122.
[20] ZHOU H, CHEN J, LU J, et al. A new rock brittleness evaluation index based on the internal friction angle and class I stress-strain curve[J]. Rock Mechanics and Rock Engineering, 2018, 51(7):2309-2316.
[21] 夏英杰, 李连崇, 唐春安, 等. 基于峰后应力跌落速率及能量比的岩体脆性特征评价方法[J]. 岩石力学与工程学报, 2016,35(6):1141-1154.
XIA Yingjie, LI Lianchong, TANG Chunan, et al. Evaluation method of rock mass brittleness characteristics based on post-peak stress drop rate and energy ratio[J]. Chinese Journal of Rock Mechanics and Engineering, 2016,35(6):1141-1154.
[22] GONG F, WANG Y, WANG Z, et al. A new criterion of coal burst proneness based on the residual elastic energy index[J]. International Journal of Mining Science and Technology, 2021, 31(4):553-563.
[23] 宫凤强, 闫景一, 李夕兵. 基于线性储能规律和剩余弹性能指数的岩爆倾向性判据[J]. 岩石力学与工程学报, 2018,37(9):1993-2014.
GONG Fengqiang, YAN Jingyi, LI Xibing. Rockburst propensity criterion based on linear energy storage law and residual elastic energy index[J]. Chinese Journal of Rock Mechanics and Engineering, 2018,37(9):1993-2014.
[24] CHEN G, JIANG W, SUN X, et al. Quantitative evaluation of rock brittleness based on crack initiation stress and complete stress-strain curves[J]. Bulletin of Engineering Geology and the Environment, 2019, 78(8):5919-5936.
[25] KUANG Z, QIU S, LI S, et al. A new rock brittleness index based on the characteristics of complete stress-strain behaviors[J]. Rock Mechanics and Rock Engineering, 2021, 54(3):1109-1128.
[26] 刘俊新, 李军润, 尹彬瑞, 等. 基于能量平衡的新脆性指标与页岩失效机制分析[J]. 岩石力学与工程学报, 2022,41(4):734-747.
LIU Junxin, LI Junrun, YIN Binrui, et al. Analysis of new brittleness index and shale failure mechanism based on energy balance[J]. Chinese Journal of Rock Mechanics and Engineering, 2022,41(4):734-747.
[27] 丁 鑫, 肖晓春, 潘一山, 等. 单轴压缩条件下不同冲击倾向性煤岩损伤与破碎能演化规律研究[J]. 采矿与安全工程学报, 2022,39(3):517-526.
DING Xin, XIAO Xiaochun, PAN Yishan, et al. Study on the evolution law of damage and crushing energy of coal and rock with different impact tendency under uniaxial compression[J]. Chinese Journal of Mining and Safety Engineering, 2022,39(3):517-526.
[28] 刘晓辉, 郑 钰, 郝齐钧, 等. 基于特征应力的准静态三轴煤岩脆性特征分析[J]. 岩石力学与工程学报, 2021,40(12):2454-2465.
LIU Xiaohui, ZHENG Yu, HAO Qijun, et al. Quasi-static triaxial coal and rock brittleness analysis based on characteristic stress[J]. Chinese Journal of Rock Mechanics and Engineering, 2021,40(12):2454-2465.
[29] 卢志国, 鞠文君, 高富强, 等. 结构性煤体间歇性破坏行为的实验及数值模拟研究[J]. 岩石力学与工程学报, 2020,39(5):971-983.
LU Zhiguo, JU Wenjun, GAO Fuqiang, et al. Experimental and numerical simulation of intermittent failure behavior of structural coal mass[J]. Chinese Journal of Rock Mechanics and Engineering, 2020,39(5):971-983.
[30] 张春会, 郑晓明. 岩石应变软化及渗透率演化模型和试验验证[J]. 岩土工程学报, 2016,38(6):1125-1132.
ZHANG Chunhui, ZHANG Xiaoming. Model and experimental verification of rock strain softening and permeability evolution[J]. Chinese Journal of Geotechnical Engineering, 2016,38(6):1125-1132.
