0 引 言
覆岩移动变形造成区域建筑物损坏,探究区域内浅部岩层协同变形有助于地表移动变形预计、降低沉陷异常区拓展[1-2]。霍尔辛赫煤矿采用工程类比法留设了较为安全的保护煤柱,而回采后的地表移动变形仍然大于预计值,部分村庄出现房屋损坏现象。究其原因为常规的地表移动变形参数对于该矿地表下沉预计不能完全适用,需对造成此类地表沉陷区异常扩展的原因及影响因素进行分析。
针对地表沉陷问题,相关学者提出各种地表移动变形破坏预测手段[3-5],主要的方法有经验分析法、概率积分法、影响函数法[6-9]。曹丽文等[10]利用神经网络定量预测了煤矿的开采沉陷。赵高博等[11]对厚松散层高强度开采引起的岩层与地表移动进行了研究,并通过现场实测值和数值模拟得出岩体与地表移动边界最终呈现出“类沙漏”形的结论。文献[12-14]研究发现含水层压缩主要造成的是地表沉陷中竖直方向的压缩,并由此提出厚松散层条件下,应当按照土层埋深和沉积年代分段划分松散层移动角量。并且采用了离散元法,计算得到厚松散层厚度越大,移动角越小的结论。文献[15-16]利用Weibull时间序列函数模型对松散层运动沉降过程进行了研究,并分为了3个阶段,解释了兖州矿区沉降规律。易四海等[17]采用数值模拟的手段,解释了厚松散层条件下开采地表下沉系数偏大的机理,强调了基岩对地表沉陷的主导作用,但是未考虑松散层内部变形特征带来的影响。针对土体发生渗透破坏流动现象,许延春[18]设计了砂土流动性试验,研究了含黏砂土的流动性,得出含黏砂土具有渗漏自愈性的结论。LSRAR等[19]引入应力折减系数,考虑土体内部颗粒间摩擦,建立土体渗透破坏理论模型,并给出相应渗透破坏水力坡降计算公式。目前,对于浅部砂层在地表沉陷中特殊运移特征鲜有研究。
笔者针对霍尔辛赫煤矿地表沉陷异常问题,采用物理相似试验研究了受采动影响后的浅部饱水砂层和其上覆黏土层流动性的协同变形情况,再通过FLUENT数值方法对物理试验进行了验证,研究了上覆黏土层形态和应力变化过程,分析地表移动变形异常机理,并总结了黏土层平错和局部隆起形成规律。本试验可供相似地质条件的地表移动变形研究参考。
1 平错隆起试验原理与参数
1.1 试验原理
霍尔辛赫煤矿3205工作面地表浅部存在近水平饱水砂层,其上下被厚层黏土加持。工作面回采后,由于采动的影响,高潜水位的砂层在水平方向产生不同沉降,造成了砂层的倾斜,在其两端产生水头差,使得该砂层可能具有流动性。如图1所示,AB两端产生水头差,地下水面高度由原来h1降到h2。
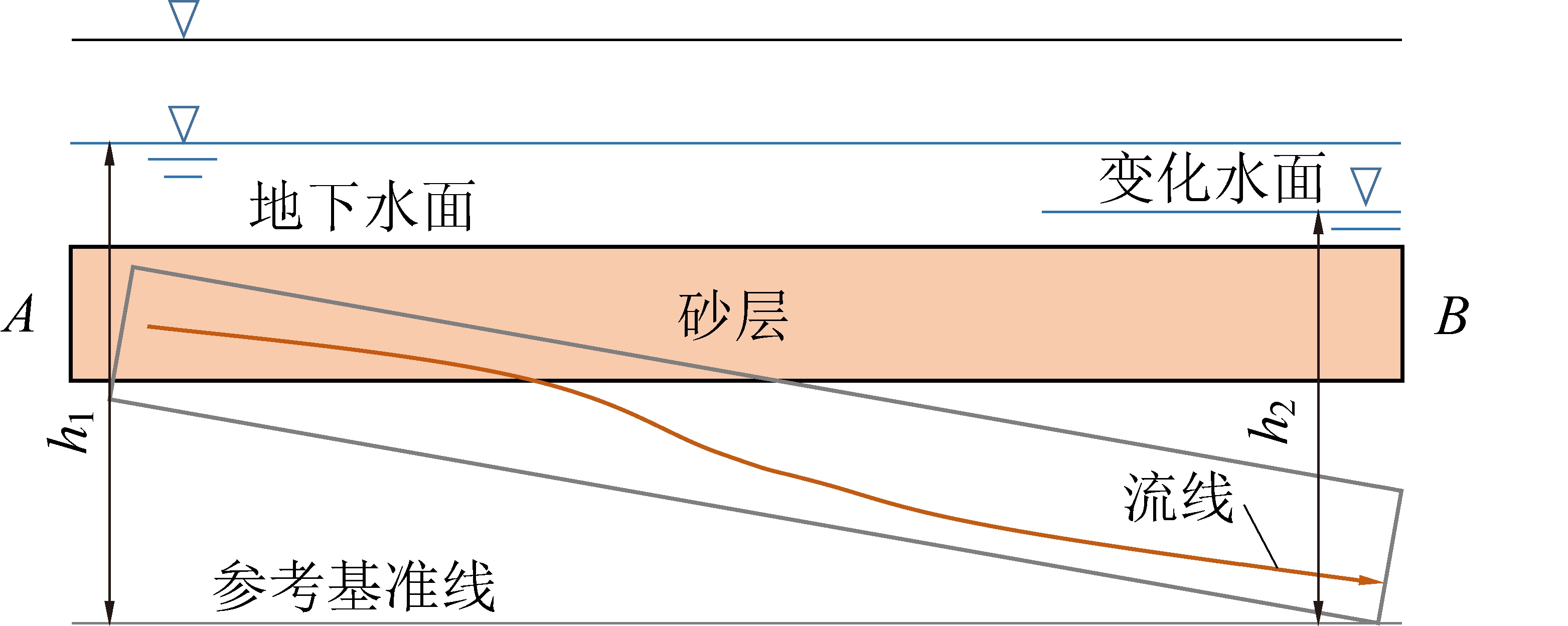
图1 饱水砂层采动变化
Fig.1 Mining variation of water saturated sand layer
造成地表移动盆地形成过程中岩层水平错动不同步,位于水平移动盆地拐点处的层间出现非连续性水平变形,岩层移动发展至地表,导致地表局部开裂和隆起。
如图2所示,为刚达到充分采动时水平煤层地表移动变形,以图2中左半部分为研究对象。A点为下沉盆地边界点,下沉值为0。B点为水平变形曲线0点,C点为倾斜曲线极值点,其垂线与B点相交。E点为CB延长线交于土层的点,位于在煤壁前方(采空区侧),并且E点下沉值接近最大下沉值的一半。O点为下沉盆地中心点,下沉值最大,D点为O点在AB直线上的投影点。
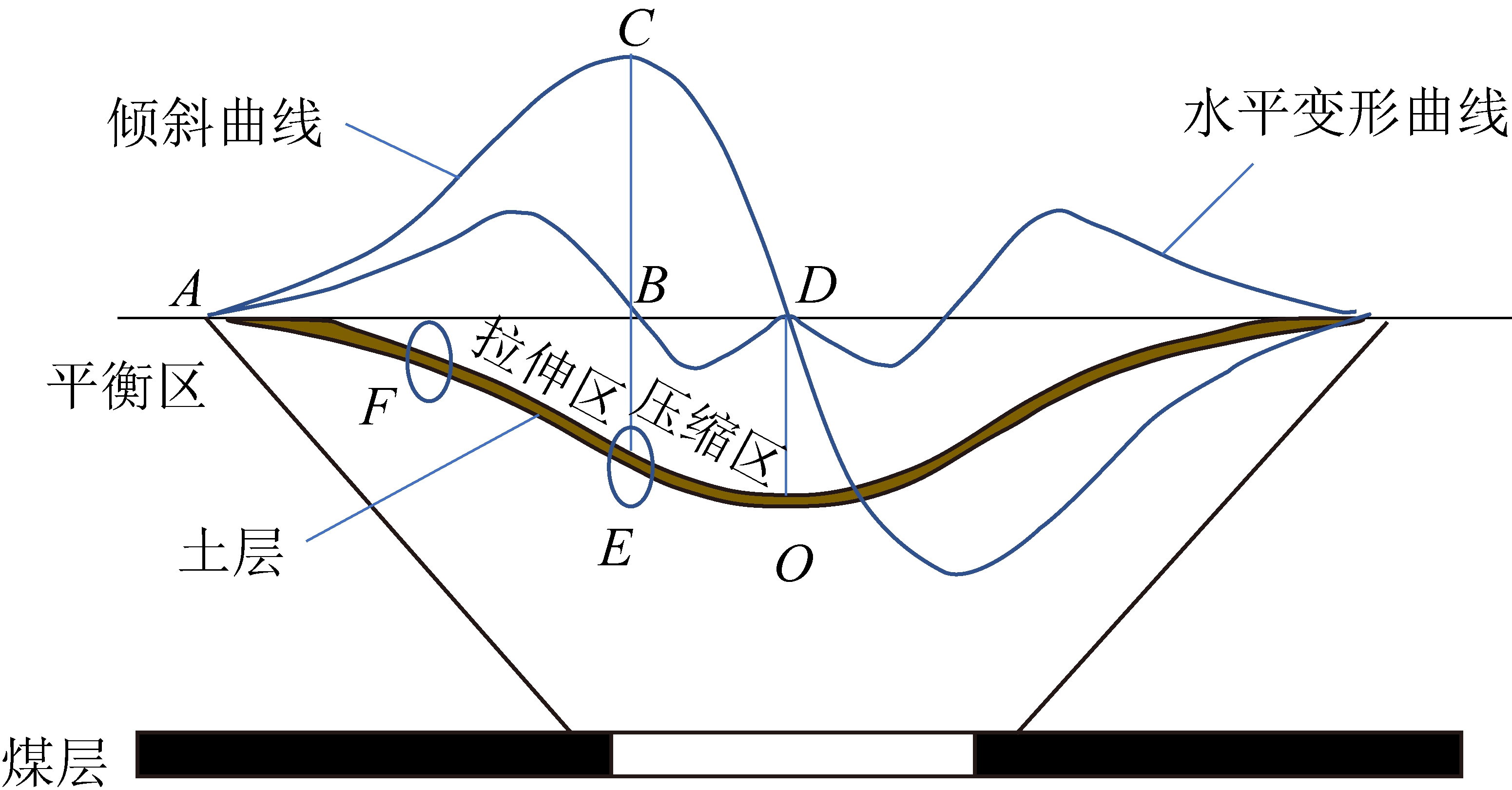
图2 水平煤层地表移动变形
Fig.2 Surface movement and deformation map of horizontal coal seam
水平变形曲线经过B点,水平变形由正变为负,说明AE段为拉伸区域,EO段为压缩区域。倾斜曲线经过C点后,CD段曲线下降速度快于AC段曲线上升速度,说明AE段长度比EO段长度大,即土层受拉伸区域比受压缩区域大。在AF近水平段为平衡区。上覆黏土层与砂层产生相对位移,在下沉盆地平衡区和拉伸区分界点F处易发生拉伸破坏,使得地表出现裂隙。
试验以该饱水砂层为研究对象,先通过测量砂的自然安息角以及计算其临界水力坡降,来研究分析自然安息角和临界水力坡降对饱和砂、黏土流动性的影响。通过在试验装置内分层装填混凝土、砂和黏土来模拟浅部基岩、砂层、黏土层,在试验装置前端进行注水加压模拟砂层倾斜产生的水头差。以饱和砂的自然安息角和临界水力坡降设定试验条件,使模拟试验中砂层移动、流砂移动,在砂层和黏土层存在速度差的情况下通过砂层颗粒间摩擦力使黏土层发生移动,试验中观察黏土层和砂层的形态变化来研究黏土层隆起、平错产生机理。
1.2 试验方案与参数
1.2.1 试验方案
此次试验分为物理相似模拟试验和数值模拟试验,共设置黏土层厚度和主体模型角度2个变量,模拟在采动的影响下,不同厚度的上覆黏土层以及变化的砂层倾角对黏土层平错距离和隆起长度的影响。试验前对主体模型注水加压,以达到砂层临界水力坡降,在不同黏土层厚度的条件下,调节主体模型角度并观察黏土层和砂层的变化情况并记录时间,记录黏土层隆起长度和平错距离。试验对3种厚度的黏土层、3种角度的主体模型进行正交试验,共9种方案。具体试验方案见表1。
表1 黏土层隆起、平错试验
Table1 Test of uplift and dislocation of clay layer
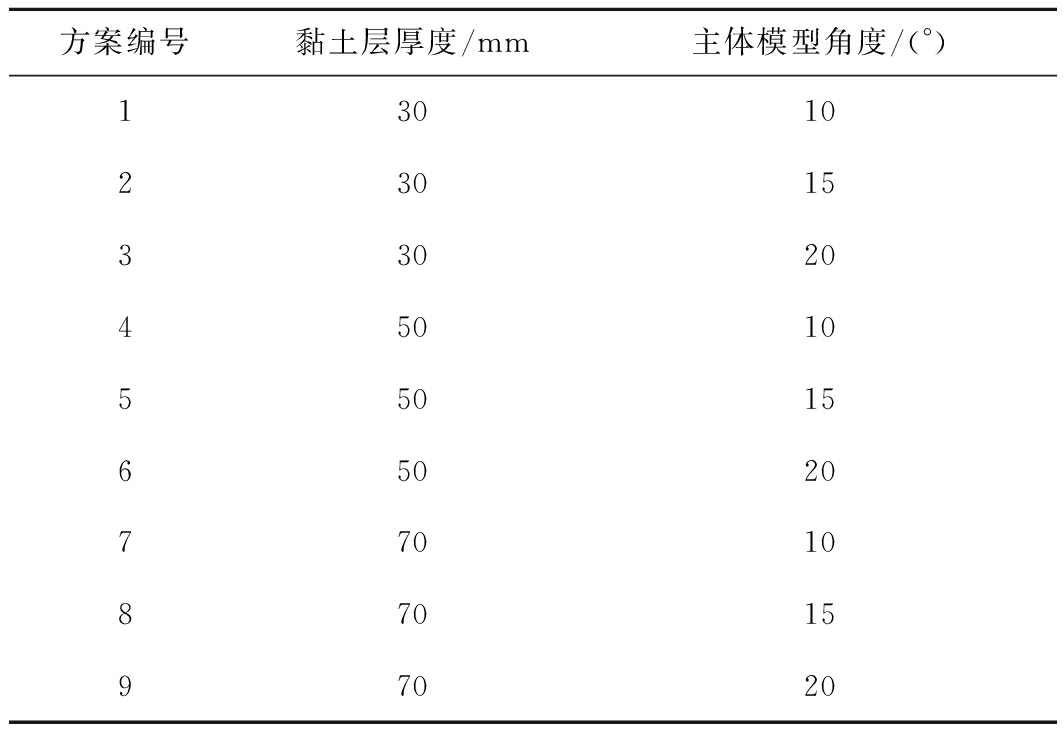
方案编号黏土层厚度/mm主体模型角度/(°)130102301533020450105501565020770108701597020
1.2.2 试验相关参数
为使试验结果明显且材料制备便捷,砂层选择粒径较大的中砂进行研究。
1)临界水力坡降。水力坡降为含水层两点间的水头差与距离之比,可通过式(1)计算。
(1)
式中:i为水力坡降,m;Δh为含水层两点间的水头差,m;L为含水层两点间的长度,m。
根据土力学理论,当含水层水位达到一定的高度时,向上的渗透力克服了向下的重力,土体就要发生浮起或破坏,俗称流土[20]。土体发生流土的水力坡降,为临界水力坡降。可通过式(2)计算。
(2)
其中:icr为临界水力坡降,m;Gs为土粒的比重;e为土粒的孔隙比。Gs本试验中取2.66,e取0.4。综合上述公式计算可得中砂临界水力坡降为1.19 m。
2)自然安息角。为了初步确定主体模型中可以发生水砂运移现象时的角度,需要确定中砂自然安息角,分别取中砂倒入小纸杯中压实,用透明有机玻璃板盖住杯口,按住并翻转纸杯,缓慢拿掉纸杯使纸杯中的砂子流出,测量沙堆的高和宽,经过计算得出饱和中砂自然安息角,结果如下:

2 黏土层平错隆起试验
2.1 物理相似模拟试验
2.1.1 物理相似模拟装置
所研发的一种模拟饱和砂、黏土平错试验装置主要由注水系统、主体模型试验台和排水系统3部分组成。①注水加压系统:注水加压系统主要由1个长500 mm,直径150 mm的有机玻璃圆柱体和塑料水管构成。②主体模型试验台:主体模型试验台主要由长1 000 mm宽和高200 mm有机玻璃U型槽、有机玻璃端盖、橡胶密封圈、加强筋、螺栓及螺母,以及底部有可调节角度的底座组成。③排水系统:通过主体模型试验台侧部的有机玻璃端盖通过端盖上面的出水口通过塑料水管连接集水器构成排水系统。上述模拟饱和砂、黏土平错试验装置如图3所示。
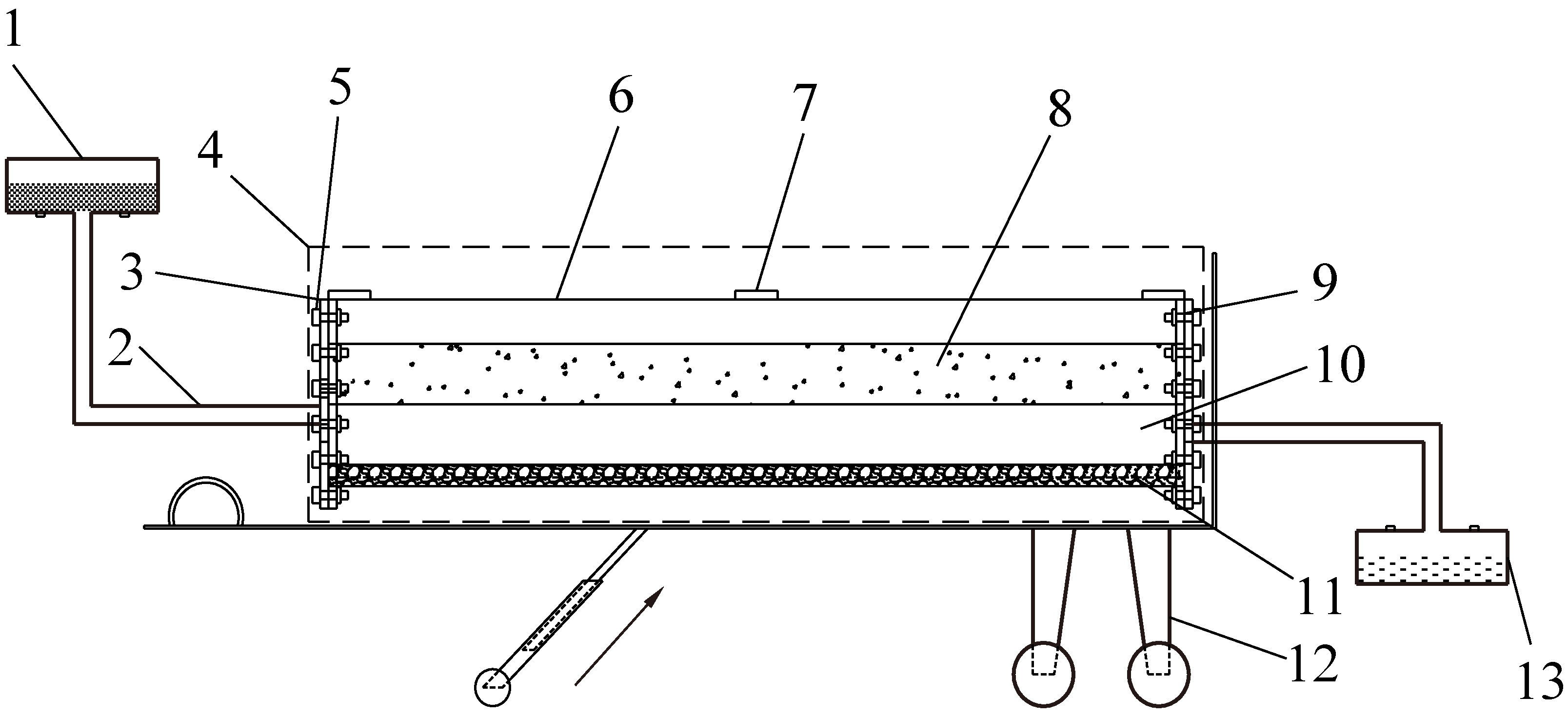
1—注水装置;2—塑料管;3—端盖;4—主体模型;5—螺栓;6—两端带法兰的有机玻璃U型槽;7—加强筋;8—黏土层;9—橡胶垫片;10—砂层;11—基岩;12—可调节角度底座;13—集水箱
图3 试验装置
Fig.3 Experimental device diagram
主体模型内需按照图3所示方式分层装填混凝土、中砂和黏土来模拟浅部基岩、砂层、黏土层。经过配比试验,确定混凝土制作所用水泥、砂子及水的质量比为6∶2∶1。将按上述比例配好的混凝土倒入模具,捣实后将其放于通风良好的地方静置一段时间。通过用粒径为0.5 mm和0.35 mm的筛子制备中砂,把中砂平铺在混凝土上层。最后经过配比试验,确定最上层黏土层黏土、砂子质量比为3∶1。
2.1.2 物理相似模拟试验流程
试验前按照上述方式搭建好模拟装置。每次试验共注水10 000 mL,开始缓慢注水黑红阀门半开,使砂层充分吸水,当水从出水口稳定流出时记录时间,此时砂层达到饱水状态,开始调节底座支架并观察黏土层和砂层的变化情况并记录时间,记录黏土层隆起长度和平错距离。同一黏土层厚度,进行3组不同主体模型角度下的试验,然后改变黏土层厚度,以控制变量。
2.2 数值模拟方法及模型
2.2.1 数值模拟试验模型
VOF模型是FLUENT多相流模型的一种。VOF模型中,在整个计算域内求解单一动量方程,所得到的速度场被所有相共用。在整个区域中求解每个计算单元中相的体积分数。由于黏土、砂为分层流动,存在明显分界面,便于观察黏土层和砂层的变化情况,故采用瞬态VOF模型进行多相流模拟。在前处理器ICEM中建立试验模型,并对其进行结构化网格划分,生成FLUENT可识别的msh文件。该模型长1 000 mm,宽170 mm,在距底部30 mm处划分黏土和砂的分界面,整个模型共划分为26 793个单元,共有25 800个节点。数值模拟计算网格剖分如图4所示。

图4 数值模拟网格剖分
Fig.4 Mesh generation of numerical simulation
数值模拟假设包括:①岩层是连续、不可压缩、均质且各向同性;②壁面不透水且对固体颗粒无吸附作用;③液态水从入口流入,且平行于模型主体。
2.2.2 数值模拟试验参数
设定在初始化充满空气的模型中,按顺序添加上砂层和黏土层2个相,按照物理相似模拟试验设定材料参数,黏土层厚度按照试验方案设定。重力加速度g=9.8 m/s2,通过改变重力场中各分力的大小来模拟模型不同角度下的移动变形情况。根据式(1),设定入口水压力为0.015 MPa,达到砂层临界水力坡降。混合压力出口,设定无滑动wall范围为位移边界条件。
3 试验结果分析
初始状态下砂层和黏土层之间无相对位移,表面平整,以模拟煤层开采前的状态,如图5所示。为了便于观察黏土层的形态变化情况,数值模拟结果在主体模型的前端和后端设置局部放大区域。
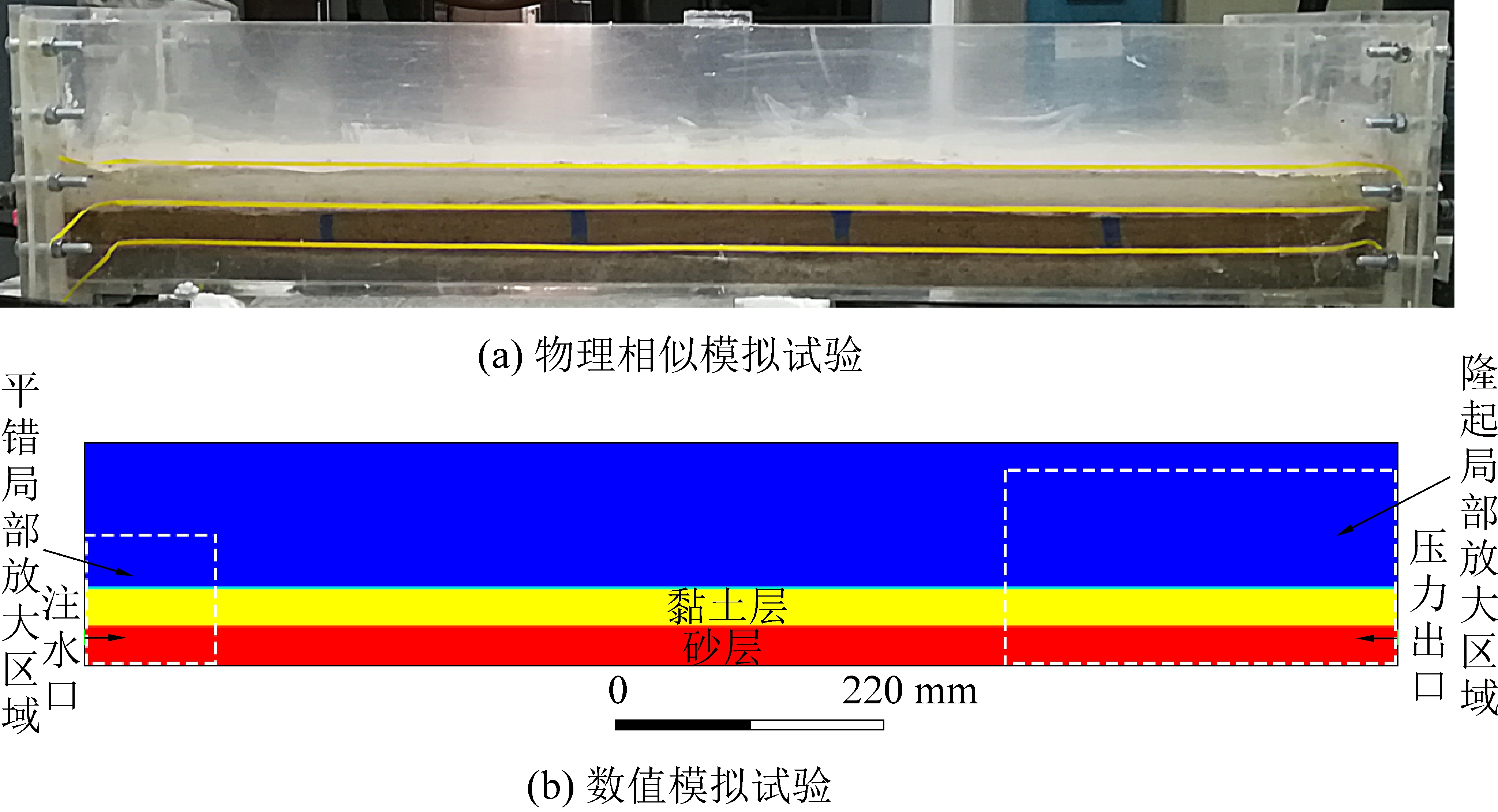
图5 数值模拟初始状态
Fig.5 Initial state of numerical simulation
3.1 隆起结果
入口水压力为0.015 MPa,t=40 s时停止运算,观察黏土层隆起现象。数值模拟结果隆起局部放大如图6所示。
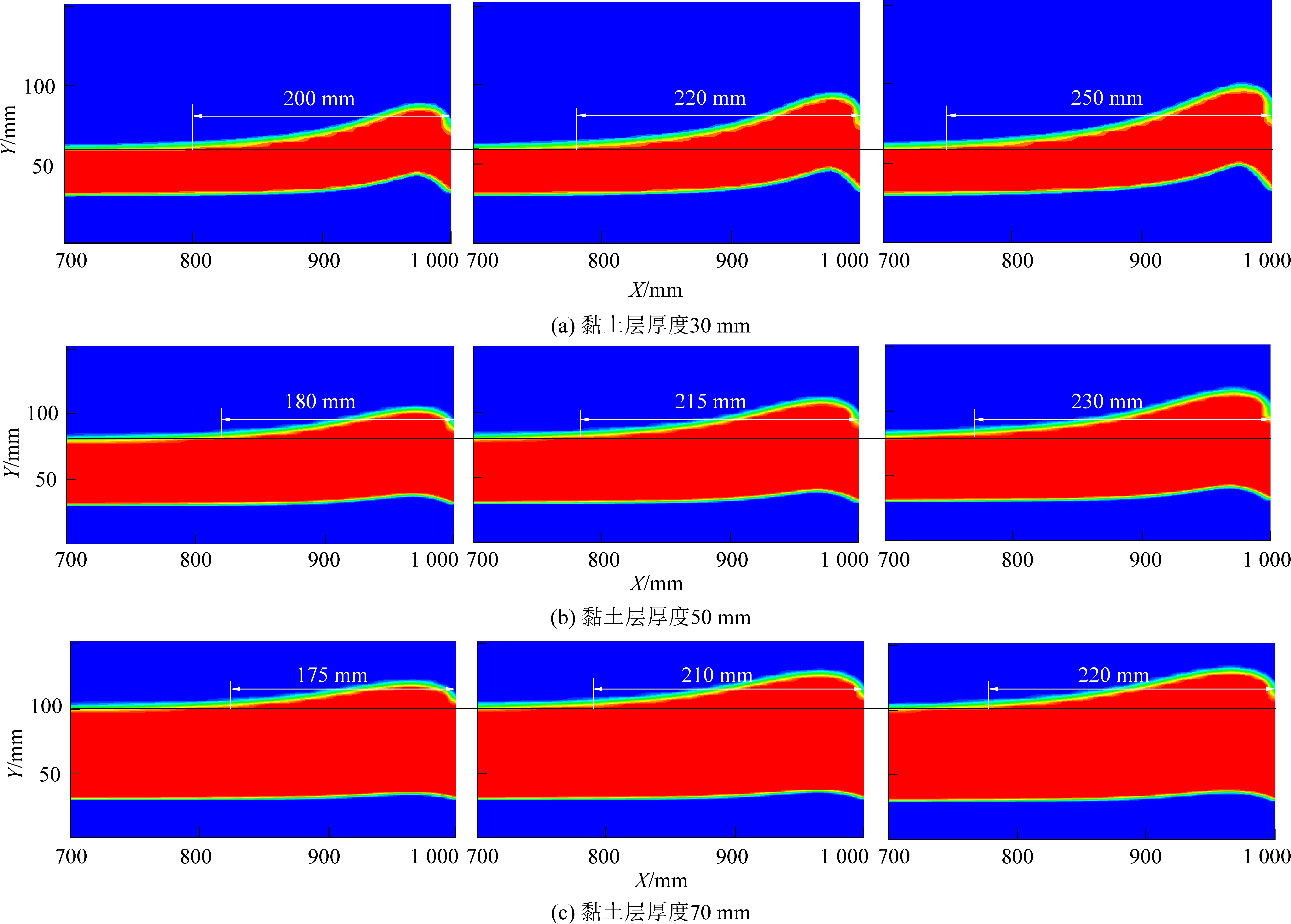
图6 黏土层隆起局部放大
Fig.6 Enlarged view of local uplift of clay layer
1)黏土层的移动变形是重力和渗透力共同作用的结果,只有在静水压力作用下,砂层达到临界水力坡降才会使砂层上部分产生流砂,流砂层和黏土层产生流速差,出现黏土层平错和隆起现象。从试验1、4、7可知,主体模型在未达到砂层自然安息角的条件下,黏土层出现了平错、隆起现象,可知自然安息角不能作为黏土层平错、隆起的主导因素。
2)通过对比不同主体模型角度条件下的模拟结果可知,黏土层厚度一定时,隆起长度随角度增加而增大,说明当角度增大时,重力平行模型向下的分力增大,使其产生更大位移,在模型后段堆积形成的局部隆起范围增大。
3)通过对比黏土层厚度为30、50、70 mm的模拟结果可知,当主体模型角度一定时,黏土层厚度越薄,其终态变形量越大,隆起长度越大,当厚度增加时,受自身重力的影响,隆起长度减小。可知上覆黏土层较薄时,其状态不稳定,易发生移动变形破坏。
4)主体模型后端隆起最高处,不同条件下黏土层与砂层隆起高度对比情况,如图7所示。
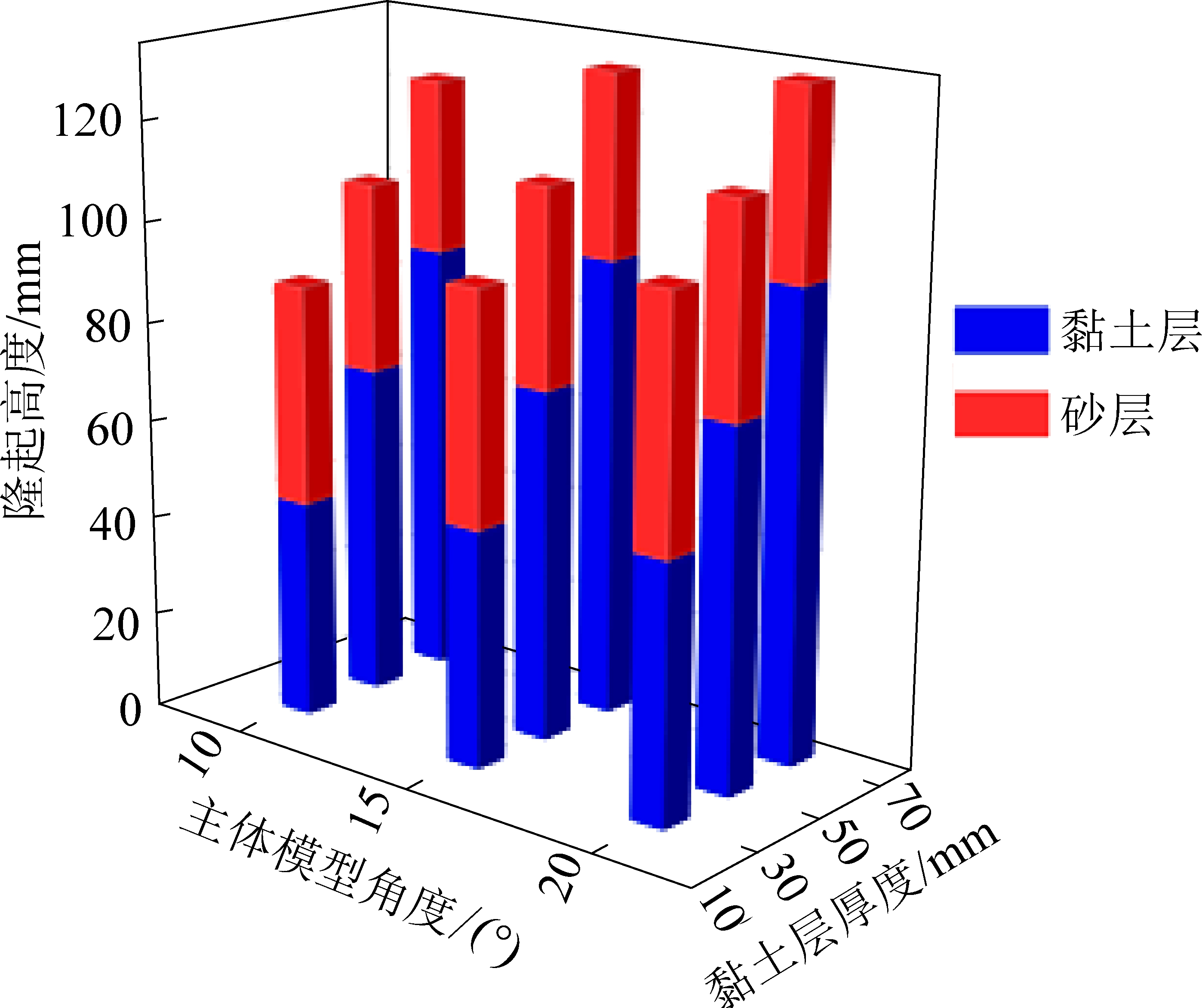
图7 黏土层与砂层隆起高度对比
Fig.7 Comparison of uplift height between clay layer and sand layer
对比可以得出,主体角度一定时,黏土层厚度越薄,总体隆起高度比较低,砂层所占比率较大,此时砂层所受上覆压力较小,易发生移动变形,随着厚度的增加,砂层高度逐渐减小,黏土层逐渐成为决定终态总体隆起高度的主导因素。黏土层厚度一定时,随着主体模型的角度增加,黏土层和砂层的高度均增加,砂层高度最大增加量为20 mm,但黏土层厚度较大时,角度对砂层高度影响较小。
5)物理相似模拟试验现象如图8所示。同数值模拟现象相同,在主体模型后端出现局部隆起现象,用直尺量取隆起长度并记录。

图8 物理试验隆起现象
Fig.8 Uplift phenomenon in physical experiment
根据物理试验和数值模拟结果,绘制出黏土层不同厚度条件下,隆起长度随主体角度变化对比曲线,如图9所示。

图9 隆起长度随主体角度变化
Fig.9 Uplift length changing with main body angle
通过图9可以得到,数值模拟与物理试验结果大致相似,变化趋势基本吻合,模拟值普遍大于试验值,黏土层厚度和主体模型角度均与隆起长度呈正相关性,主体模型角度对黏土层隆起长度影响更大。
3.2 平错结果
入口水压力为0.015 MPa,t=40 s时停止运算,观察黏土层平错现象。数值模拟结果平错局部放大如图10所示。
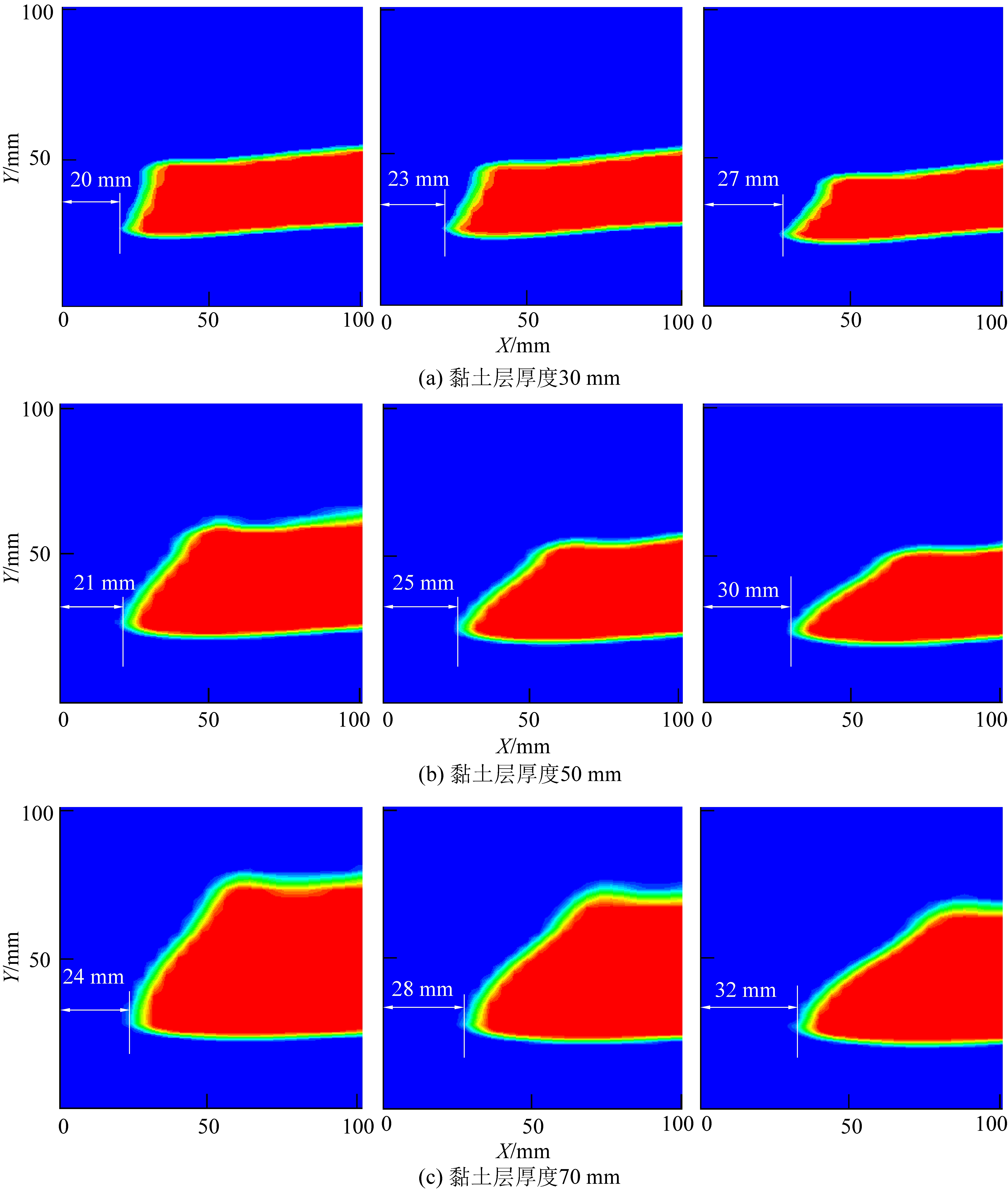
图10 黏土层平错局部放大
Fig.10 Enlarged view of local dislocation of clay layer
1)从试验1、4、7可知,同隆起现象相同,在主体模型未达到自然安息角的条件下,黏土层出现了平错现象。说明在重力和渗透力2种体力作用下,砂层与上覆黏土层产生相对错动。在静水压力未达到水力坡降时,砂层达到自然安息角只沿厚度方向在砂层内部发生线性错动,砂层上下面出现错动值,使黏土层移动,但移动量较小,无明显平错现象;达到水力坡降时,砂层活化产生流砂现象,黏土层平错值会增大。
2)通过对比不同主体模型角度条件下的模拟结果可知,黏土层厚度一定时,平错距离随主体模型角度增加而增大,说明当主体模型角度增大时,由于重力平行模型向下的分力增大,使其更易发生平错,且终态平错距离变大。
3)通过对比黏土层厚度为30、50、70 mm的模拟结果可知,当主体模型角度一定时,黏土层平错距离随黏土层厚度增大而增大,说明当黏土层厚度增加时,由于自身重力增大,导致平错方向的力增大,使其更易发生平错,且终态平错距离变大。
4)物理相似模拟试验现象如图11所示。同数值模拟现象相同,在主体模型前端出现平错现象,用直尺量取平错距离并记录。

图11 物理试验平错现象
Fig.11 Dislocation phenomenon in physical experiment
根据物理试验和数值模拟结果,绘制出黏土层不同厚度条件下,平错距离随主体角度变化对比曲线,如图12所示。
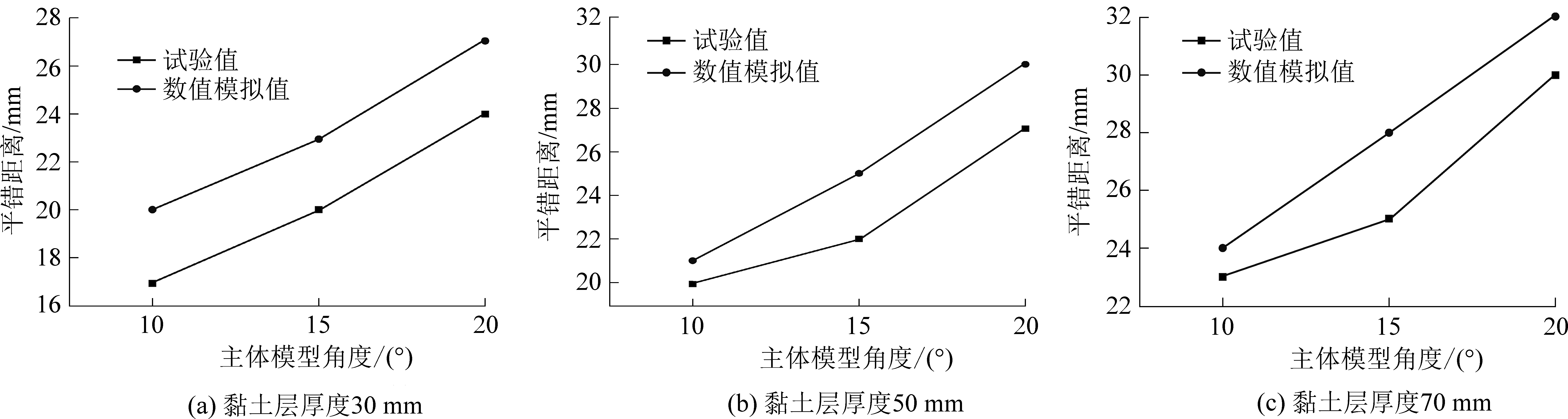
图12 平错距离随主体角度变化
Fig.12 Dislocation distance changing with main body angle
通过图12可得,数值模拟与物理试验结果大致相似,变化趋势基本吻合,模拟值普遍大于试验值,同隆起现象相同,黏土层厚度和主体模型角度均与平错距离呈正相关性,主体模型角度对黏土层平错距离影响更为明显。说明饱水砂层受采动下沉和倾斜成为流砂后,采动持续影响下,砂层倾角的持续增大,成为层间错动加大、水平移动增加和地表沉陷影响范围扩大的主导因素。
3.3 应力变化规律
仿真试验的压应力场分布可作为解释模型试验台黏土层移动变形过程的依据,结合特征点应力随时间变化规律,用以分析黏土层平错、隆起现象形成过程,可明确结果中出现的特殊现象机理。选取模型x=1,y=0处的特征点,该点在模型隆起范围之内且应力变化明显,具有针对性。在此处布置监测点,绘制不同黏土层厚度以及主体模型角度应力随时间变化曲线,如图13所示。
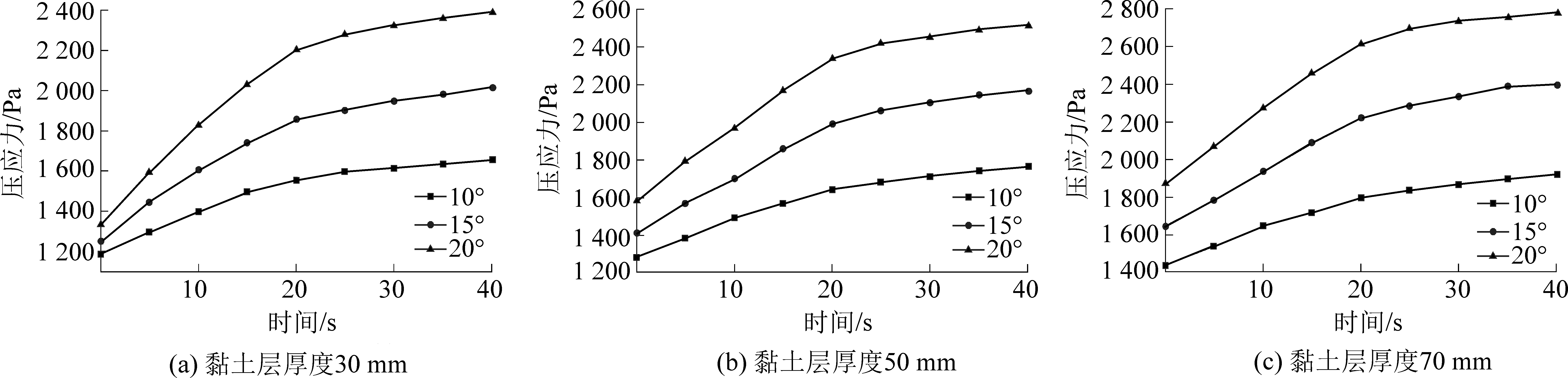
图13 应力随时间变化曲线
Fig.13 Stress change with time
1)随着平错、隆起现象的产生,应力随时间不断增大,t=20 s时,应力曲线开始趋于平缓,此时隆起现象明显,基本达到最大隆起高度,t=40 s时,应力达到最大,黏土层30 mm时,最大应力分别为1 650、2 012、2 391 Pa,黏土层50 mm时,最大应力分别为1 760、2 165、2 515 Pa,黏土层70 mm时,最大应力分别为1 912、2 399、2 784 Pa。
2)由初始状态到终态,不同主体角度模型之间,应力差逐渐增大,黏土层30 mm时差值增加量最大,增加近4倍,说明主体角度变化对隆起范围影响明显;黏土层厚度一定时,同一时刻,随着主体角度的增大,应力逐渐增大,可知主体角度越大,隆起的范围和高度越大,且因为砂层流速变快,隆起变形速率加快。
3)通过对比上组曲线图,同一时刻,相同主体角度条件下,黏土层厚度与应力呈正相关性,但随着厚度增加,应力曲线斜率减小,可知黏土层越厚,越不易发生移动变形破坏,黏土层终态隆起高度增加,隆起范围逐渐减小。
4 结 论
1)研发了一种室内研究浅部饱水砂层和上覆黏土层协同移动变形规律的物理模拟试验装置,结合数值仿真模拟,形成了一种研究黏土层平错以及局部隆起的方法。
2)通过测定砂的自然安息角以及计算其临界水力坡降,研究了对饱和砂、黏土流动性的影响。结果显示,自然安息角不能作为黏土层平错、隆起的主导因素;黏土层的移动变形是重力和渗透力共同作用的结果,只有在静水压力作用下,砂层达到临界水力坡降才会使砂层活化流动,流砂层和黏土层产生流速差,出现黏土层平错和隆起现象。
3)主体模型角度一定时,黏土层厚度越小越易发生移动变形破坏,局部隆起长度越大,但终态隆起高度比较低;当黏土层厚度增加时,隆起范围减小,平错距离变大;黏土层厚度一定时,黏土层隆起长与平错距离都与主体模型角度呈正相关性,且随角度的增加,变形速率逐渐加快。
4)饱水砂层成为流砂后,采动持续影响下,砂层倾角的持续增大,成为层间错动加大、水平移动增加和地表沉陷影响范围扩大的主导因素。
[1] 许延春,戴华阳.沉陷控制与特殊开采[M].徐州:中国矿业大学出版社,2017.
[2] 左建平,周钰博,刘光文,等.煤矿充填开采覆岩连续变形移动规律及曲率模型研究[J].岩土力学,2019,40(3):1097-1104,1220.
ZUO Jianping,ZHOU Yubo,LIU Guangwen,et al.Study on continuous deformation movement law and curvature model of overburden in coal mine filling mining[J].Rock Mechanics,2019,40(3):1097-1104,1220.
[3] 赵启峰,孟祥瑞,赵光明,等.厚松散层下开采沉陷预测模型的研究及应用[J].中国煤炭,2008(5):36-38,43,4.
ZHAO Qifeng,MENG Xiangrui,ZHAO Guangming,et al.Research and application of mining subsidence prediction model under thick loose layer[J].China Coal,2008(5):36-38,43,4.
[4] 左建平,孙运江,钱鸣高.厚松散层覆岩移动机理及“类双曲线”模型[J].煤炭学报,2017,42(6):1372-1379.
ZUO Jianping,SUN Yunjiang,QIAN Minggao.Overburden movement mechanism and "hyperbolic like" model[J].Journal of China Coal Society,2017,42(6):1372-1379.
[5] 许国胜,李德海,侯得峰,等.厚松散层下开采地表动态移动变形规律实测及预测研究[J].岩土力学,2016,37(7):2056-2062.
XU Guosheng,LI Dehai,HOU Defeng,et al.Measurement and prediction of dynamic surface movement and deformation law under mining under thick loose layer[J].Rock Mechanics,2016,37(7):2056-2062.
[6] 李春意,高永格,崔希民,等.云驾岭矿厚煤层综采地表沉陷时空演化规律研究[J].采矿与安全工程学报,2019,36(1):37-43,50.
LI Chunyi,GAO Yongge,CUI Ximin,et al.Study on temporal and spatial evolution law of surface subsidence in fully mechanized mining of thick coal seam in Yunjialing mine[J].Journal of Mining & Safety Engineering,2019,36(1):37-43,50.
[7] 郭增长,谢和平,王金庄.极不充分开采地表移动和变形预计的概率密度函数法[J].煤炭学报,2004,29(2):155-158.
GUO Zengzhang,XIE Heping,WANG Jinzhuang.Probability density function method for prediction of surface movement and deformation under extremely inadequate mining[J].Journal of China Coal Society,2004,29(2):155-158.
[8] 李春意,高永格,崔希民.基于正态分布时间函数地表动态沉陷预测研究[J].岩土力学,2016,37(S1):108-116.
LI Cunyi,GAO Yongge,CUI Ximin.Prediction of dynamic surface subsidence based on normal distribution time function[J].Rock Mechanics,2016,37(S1):108-116.
[9] 刘宝琛,戴华阳.概率积分法的由来与研究进展[J].煤矿开采,2016,21(2):1-3.
LIU Baochen,DAI Huayang.Origin and research progress of probability integral method[J].Coal Mining Technology,2016,21(2):1-3.
[10] 曹丽文,姜振泉.人工神经网络在煤矿开采沉陷预计中的应用研究[J].中国矿业大学学报,2002,31(1):26-29.
CAO Liwen,JIANG Zhenquan.Application of artificial neural network in coal mining subsidence prediction[J].Journal of China University of Mining & Technology,2002,31(1):26-29.
[11] 赵高博,郭文兵,娄高中,等.厚松散层高强度开采岩层与地表移动模拟[J].中国安全科学学报,2018,28(1):130-136.
ZHAO Gaobo,GUO Wenbing,LOU Gaozhong,et al.Simulation of high-strength mining strata and surface movement in thick and loose layers[J].China Safety Science Journal,2018,28(1):130-136.
[12] 许延春,张玉卓.应用离散元法分析采矿引起厚松散层变形的特征[J].煤炭学报,2002,27(3):268-272.
XU Yanchun,ZHANG Yuzhuo.Analysis of deformation characteristics of thick loose layer caused by mining by discrete element method[J].Journal of China Coal Society,2002,27(3):268-272.
[13] 许延春,刘世奇,高玉兵,等.厚松散层内部微变形规律研究[J].煤炭科学技术,2014,42(10):10-13,23.
XU Yanchun,LIU Shiqi,GAO Yubing,et al.Study on micro deformation law of thick loose layer[J].Coal Science and Technology,2014,42(10):10-13,23.
[14] LI Xudong,XU Yanchun,JIE Yuxin.Test on Water-Level Stabilization and Prevention of Mine-Shaft Failure by Means of Groundwater Injection[J].Geotechnical Testing Journal,2014,37(2):319-332.
[15] 张文泉,刘海林,赵 凯.厚松散层薄基岩条带开采地表沉陷影响因素研究[J].采矿与安全工程学报,2016,33(6):1065-1071.
ZHANG Wenquan,LIU Hailin,ZHAO Kai.Study on Influencing Factors of surface subsidence in strip mining of thick loose layer and thin bedrock[J].Journal of Mining & Safety Engineering,2016,33(6):1065-1071.
[16] 白 斌,张文泉.厚松散层开采松散层沉降时间序列模型研究[J].煤炭技术,2018,37(9):176-177.
BAI Bin,ZHANG Wenquan.Study on time series model of loose layer settlement in thick loose layer mining[J].Coal Technology,2018,37(9):176-177.
[17] 易四海,郑志刚,滕永海.厚松散层条件下综放开采地表沉陷规律与机理[J].煤矿开采,2011,16(4):9-12.
YI Sihai,ZHENG Zhigang,TENG Yonghai.Surface subsidence law and mechanism of fully mechanized top coal caving mining under thick loose layer[J].Coal Mining Technology,2011,16(4):9-12.
[18] 许延春.含黏砂土流动性试验[J].煤炭学报,2008,33(5):496-499.
XU Yanchun.Fluidity test of clayey sand[J].Journal of China Coal Society,2008,33(5):496-499.
[19] JAHANZAIB Israr,BUDDHIMA Indraratna.Study of critical hydraulic gradients for seepage-induced failures in granular soils[J].Journal of Geotechnical and Geoenvironmental Engineering,2019,145(7).
[20] 陶高梁,李 进,崔惜琳.不同颗粒级配的砂土渗流破坏特性[J].土木工程与管理学报,2019,36(2):90-97.
TAO Gaoliang,LI Jin,CUI Xilin.Seepage failure characteristics of sand with different particle sizes[J].Journal of Civil Engineering and Management,2019,36(2):90-97.
