0 引 言
断层等地质构造对岩层的完整性产生一定的破坏,进而对煤炭资源的回采产生一定的影响。矿井突水、瓦斯突出等地质灾害的发生与断层等地质构造有着密切的联系[1]。通过对研究区的构造复杂程度进行研究,进而避免断层等地质构造引起的灾害困扰[2-3]。今年来国内外诸多学者对构造复杂程度评价做了大量的研究工作[4-6],并且取得了一定的成果,比如刘令生[7]、姚振兴等[8]、李新凤等[9]利用相似维对矿井构造网络的复杂程度进行了预测研究,为煤矿安全开采提供了依据;有学者[10-13]利用灰色模糊综合评价方法建立了研究区地质构造的定量预测模型;还有学者基于层次分析法(AHP)对研究区的构造复杂程度进行了定量评价[14-15],刘伟等[16]采用独立性权系数法确定各评价指标所占权重,通过ArcGIS建立了矿井构造复杂程度定量评价模型,上述方法具有各自的优缺点,但也存在一定的缺点,基于上述情况,笔者将层次分析法(AHP)与熵权法二者结合,弥补2种方法各自的弊端,以陕北侏罗纪煤田沙梁井田为例,结合研究区的构造特点、物探监测及目前实际揭露的构造情况,选取断层分维值、断层强度、断层密度3个指标对断层这一因素进行评价,利用层次分析法(AHP)法构建了评价指标体系,并对各个评价指标的权重进行计算,然后再利用熵权法进行耦合分析,最终综合确定评价指标,进一步对研究区构造复杂程度进行了评价预测。
1 研究区构造概况
沙梁井田处于鄂尔多斯盆地东缘河东断褶带西侧,伊陕单斜东北角与乌拉山-呼和浩特断陷的结合带位置(图1)。井田构造形态为一向斜断陷带,主要受井田南北两条正断层(DF1、DF2)控制,断陷带内发育不同级次断裂构造,断陷带南北部为向西南方向缓倾斜的单斜构造,构造复杂程度为“中等”类型,研究区构造纲要图如图2所示。

图1 研究区交通位置
Fig.1 Traffic location of study area
研究区含煤地层沿走向、倾向的产状有一定变化,地层倾角一般1°~3°,局部地段地层倾角5°~8°,对矿井正常安全回采不能构成影响,区内无岩浆侵入迹象,含煤地层不受岩浆岩的影响,局部发育宽缓的波状起伏。结合勘探资料以及物探资料结果显示,该井田内断层构造比较发育,已发现断层63条,具体统计结果见表1。
表1 断层数量统计
Table 1 Statistics of number of faults
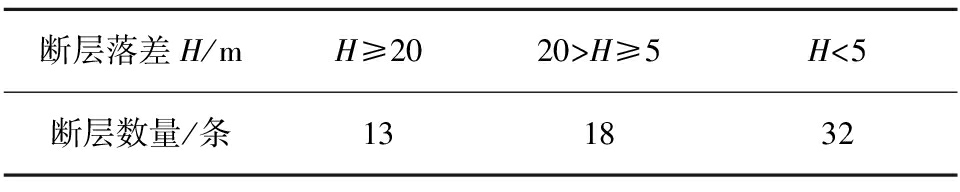
断层落差H/mH≥2020>H≥5H<5断层数量/条131832

图2 研究区构造纲要
Fig.2 Structural outline map of the study area
2 研究区构造复杂程度定量评价
2.1 评价指标选取
断层、褶曲、岩浆岩以及陷落柱等是影响构造复杂程度的主要因素,研究区的构造复杂程度主要由以上因素的发育程度决定。结合研究区现有的勘探资料和生产资料中获取的可靠数据,可知,区内未发现岩浆岩以及隐伏陷落柱等地质构造,故本次评价主要从断层这一方面入手,具体选取了3个评价指标,即:断层分维值、断层密度、断层强度组成的评价因素集。
2.1.1 断层分维值
分形理论作为断裂构造空间分布和几何结构特征定量表征的一种手段,常被用于表征分形目标的复杂程度,断层分维值与断裂构造的发育程度呈正相关关系[17]。
(1)
式中:N(ε)为一个小方格内划分的网格中具有构造迹线数目;ε为不断缩小的网格边长,m。
将研究区域分割为1 000 m×1 000 m、500 m×500 m和250 m×250 m的网格单元,依次统计不同大小网格单元中的断层数量,最终得到不同网格大小单元对应的N(ε)值,将其投放到ln N(ε)-ln ε坐标系中,得一拟合直线,用最小二乘法解算拟合直线的斜率,其绝对值即为所求单元的相似维Ds。
具体方法:首先通过Autocad采用断层平面变形系数方法,按照经纬网,将研究区划分为1 000 m×1 000 m的区块,统计每个方格中断层数目,投放到lg ε-lg N(ε)的坐标系中,然后将小方格接着划分为500 m×500 m、250 m×250 m的方格,根据不同边长ε,统计出每个块段内有断层迹线穿过的网格数N(ε),记录每一级别的N(ε),把它们投放到lg N(ε)-lg ε坐标系中,可得到1条拟合直线,取该直线斜率的绝对值即为该线段的相似维Ds(图4)。
由图5可以看出,研究区内煤层的断层分维值区间为0~3.6,断层分维值的变化具有一定的规律,等值线的变化方向与构造线的主体方向接近一致,断层长度大、密度高的部位,对应的分维值就相对较高;反之,断层密度低的部位分维值就相对较低。
利用断层分维可以反映其空间的分布情况及发展演化程度,研究区北部和中部发育有2条相对比较大的断层,中西部地区断层构造相对比较发育,密度相对也较高,分维值较高,发育程度复杂。南下部区域断层相对不发育,断层分维值低,复杂程度相对简单。

图3 分维评价块段划分示意
Fig.3 Schematic of fractal dimension evaluation

图4 研究区内某单元的回归直线图
Fig.4 Regression line graph of a unit in the study area
2.1.2 断层强度指数
断层强度指数是单元面积内所有断层的延伸长度及其落差高度的乘积之和。断层强度既要研究断层数量,又要探究断层落差和水平延伸长度,能够综合体现断层的发育特征,其计算公式[16]为
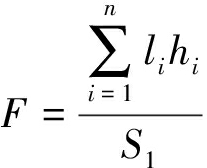
(2)
式中:li为统计单元内第i条断层水平延伸长度,m;Hi为统计单元内第i条断层断层落差,m;S1为统计单元面积,m2;n为断层条数,条。
由断层强度指数等值线图可以看出:研究区内断层强度指数为0~0.7,且研究区内断层强度指数多大于0.25,从图中可以看出研究区东部区域的断裂强度指数要远远低于研究区中西部区域的断裂强度指数,研究区南下部区域断层不发育。
2.1.3 断层密度
断层密度主要是反应一定范围内的煤储层完整性,是单位面积内发育断层的条数。断层密度越大的区域,说明煤层被断层破坏程度较为严重,煤层的形态和厚度都会受到其产生的影响;反之则说明煤层被断层破坏程度较小,保持状态和完整性相比都能够较好一些。断层密度计算式[10]为
(3)
式中:N为断层条数;A为网格面积,图3中为250 m×250 m。
由断层密度等值线图可以看出:研究区中西部局部区域地质构造发育,呈现一定的聚集性,南下部区域断层发育较弱。
2.2 数据归一化处理
基于断裂构造的定量评价,为了能够消除各评价指标对构造复杂程度评价结果的影响,对各评价指标进行归一化处理。考虑到选取3个影响因素断层分维值Ds、断层强度指数F、断层密度M与构造复杂程度呈正相关,故采用最小-最大标准化方法对以上指标进行归一化处理[18-19]:
(4)
式中:wi为第i个归一化后构造评价指标;xi为第i个归一化前构造评价指标;xi,max为第i个归一化前评价指标最大值;xi,min为第i个归一化前评价指标最小值。
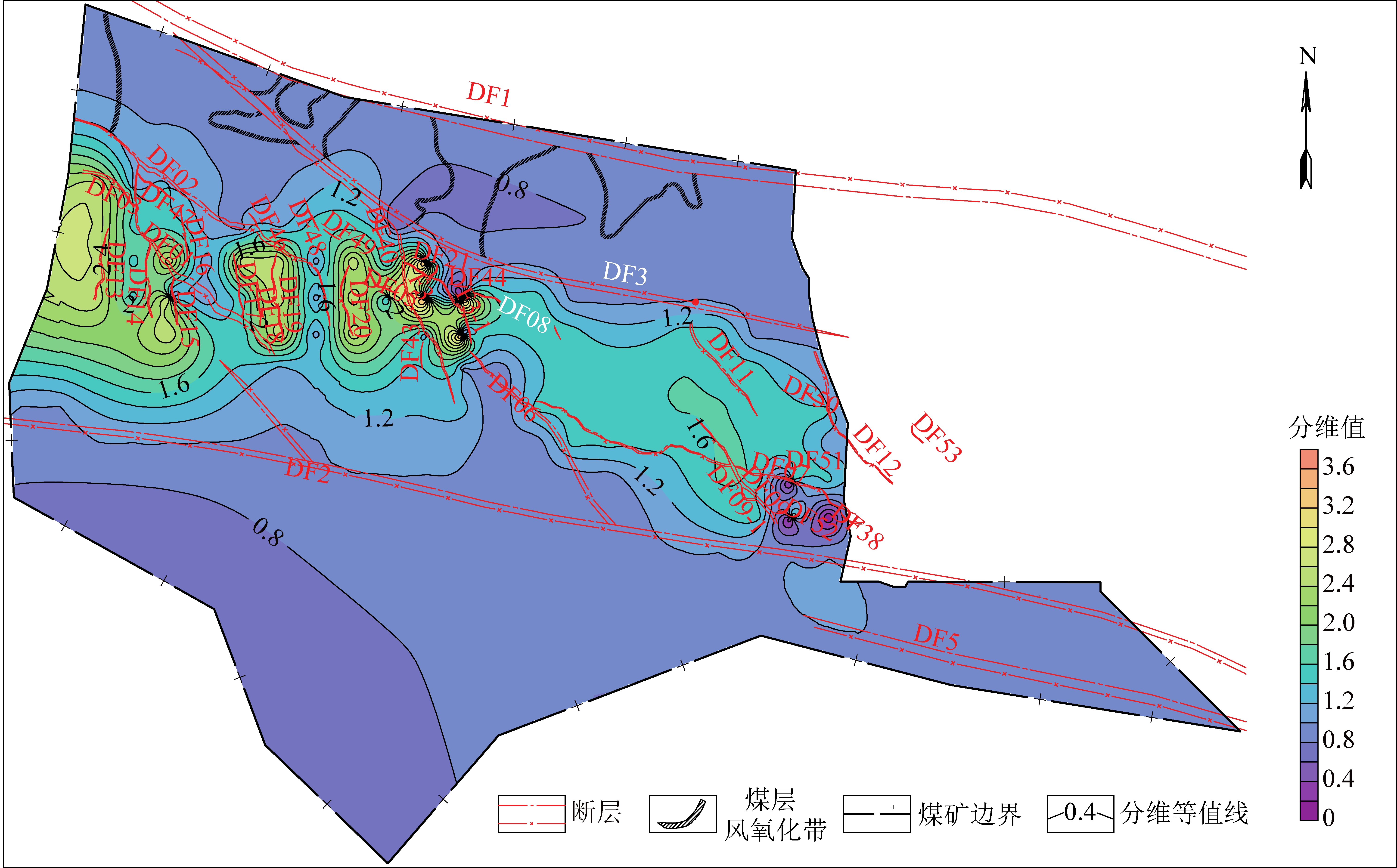
图5 断层分维值等值线
Fig.5 Contour map of fault fractal dimension value

图6 断层强度等值线
Fig.6 Contour of fault strength

图7 断层密度等值线
Fig.7 Fault density contour
表2 归一化后各单元指标的统计值
Table 2 Statistical value of each unit index after normalization
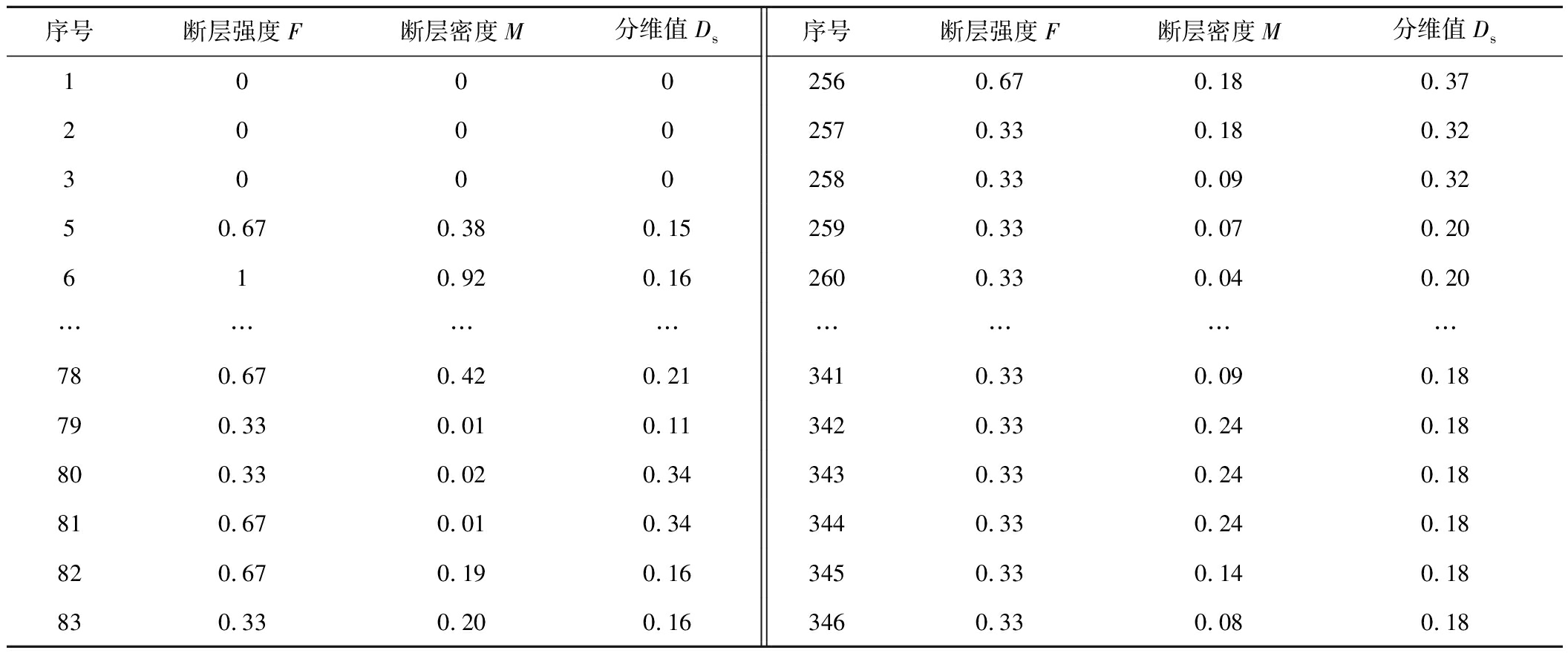
序号断层强度F断层密度M分维值Ds序号断层强度F断层密度M分维值Ds10002560.670.180.3720002570.330.180.3230002580.330.090.3250.670.380.152590.330.070.20610.920.162600.330.040.20……………………780.670.420.213410.330.090.18790.330.010.113420.330.240.18800.330.020.343430.330.240.18810.670.010.343440.330.240.18820.670.190.163450.330.140.18830.330.200.163460.330.080.18
3 AHP-熵权法综合评价
3.1 权重的确定
3.1.1 AHP确定权重
将研究对象按照目标层、准则层、决策层分别划分为A层次、B层次、C层次,建立复杂程度定量评价指标体系模型(图8)。研究对象即为模型的目标层为井田构造复杂程度评价,即A层次;模型的准则层包含3个定量指标,分别为断裂分维值Ds、断层强度指数F、断层密度M,即B层次;模型的决策层为3个定量指标的数值具体范围,即C层次。

图8 构造复杂程度定量评价指标体系
Fig.8 Construct a quantitative evaluation index system for complexity
根据各主控因素对井田构造复杂程度的影响情况,建立井田构造复杂程度系数的AHP判断矩阵Q,即:

上述矩阵可以看出矩阵是正互反矩阵,从构建判断矩阵所用的标度来判断构建正互反矩阵在逻辑上是否合理,由此可以得到B1,B2,B3的相应比较判断矩阵。求出判断矩阵的最大特征值λmax及其所对应的特征向量w=[w1 w2 w3]T,将w标准化后得到权重向量w′;计算一致性指标CI,来进一步得出判断的准确性[17]。
(5)
式中,m为Q的阶数。
表3 平均随机一致性指标RI值
Table 3 Average random consistency index RI value
n1234567RI000.520.891.121.261.36
根据表3,得到RI值,计算出一致性比率CR=CI/RI。当CR<0.1时,就可以说权重系数有效,判断矩阵Q的一致性是合理的;其余的情况就要进行修改,使得一致性合理为止。
表4 判断矩阵一致性检验指标
Table 4 Judgment Matrix Consistency Test Index
λmaxCICRA~B(i=1~3)3.038 5110.019 2560.037 03
从表4得出,CR<0.1,一致性是合理的。通过以上判断矩阵得到的影响研究区构造复杂程度的各主控因素的权重值见表5。
表5 AHP构造复杂程度评价指标权重赋值
Table 5 AHP structure complexity evaluation index weight assignment
构造评价指标断层强度F断层密度M分维值Ds权重0.104 7290.258 2850.636 986
3.1.2 熵权法确定权重
熵权是利用熵值计算指标的变异程度,根据各指标的变异程度赋予权值。因素之间的差异性越大,熵权就会越大,其对评价结果的影响也会越大[20-22]。
根据各主控因素对井田构造复杂程度的影响情况,总共有346个评价对象,3个评价指标,根据归一化处理公式,采用EXCEL软件对矩阵R=(Xij)m×n进行标准化,得到标准后的R矩阵为:

对于第j个指标,信息熵ej为
(6)
式中,Pij为第j个指标下第i个评价指标值所占权重。
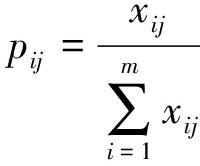
(7)
根据熵的计算公式,得出各指标的熵值向量ej如下:
ej =[ 0.881 3,0.821 8,0.861 5 ]T
m个评价对象,n个评价指标,第j个指标的熵权为:
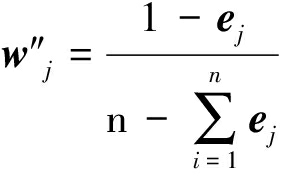
(8)
wj=[ 0.272 6,0.409 4,0.318 0 ]T
表6 熵权法构造复杂程度评价指标权重赋值
Table 6 Entropy method constructs evaluation index weight assignment of complexity degree
评价指标断层强度F断层密度M分维值Ds权重0.272 60.409 40.318 0
3.1.3 AHP-熵权法耦合确定权值
AHP法实质是一种主观赋权法,由于主观赋权方法易受专家经验知识的影响,其主观性较强,在具体应用中,会因为客观因素的特殊性、复杂性和多变性,影响它们相对重要性程度的准确判断,这样就会导致对各项指标提供的信息量参考不全面,得出的权重极有可能不准确,不客观;熵权法是一种客观赋权法,克服了人为的因素,但又过于强调各项评价指标数据之间的内部变化,缺乏对实际情况的针对性分析,为避免单一方法计算指标权重的不足,将2种方法结合,分别采用AHP法和熵权法确定各项主控因素的主观权重和客观权重,通过组合赋权的方法对AHP法和熵权法得到的权重结果进行综合分析,集合了AHP法和熵权法的优点,最终得到更加符合实际情况的权重值[23-24]。
若AHP法得出的权重排序和熵权法得出的一样,采用熵权法的权重系数,能够有效避免主观因素对指标权重系数的影响,若两者得到的权重系数排序不完全一致时,可采用AHP法-熵权法耦合确定权值,此时,能够综合AHP法与熵权法两者各自的优点,使得多指标综合评价的权数的确定更加准确合理[22]。
由式(9)将AHP法与熵权法的计算权值进行耦合,耦合结果见表7。耦合权值与AHP法分析权值在重要程度排序上完全一致,而且结合了熵权客观赋权的优点,弱化了断层密度这一指标权重。耦合后的权值突出了分维数这一指标在构造复杂程度评价预测中的决定性作用[25]。
采用乘数合成归一法将AHP法与熵权法的权值进行耦合[3-4,22](式9)
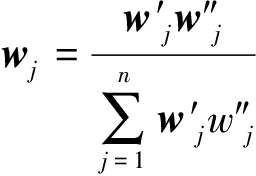
(9)
表7 不同方法构造复杂程度评价指标权重赋值结果
Table 7 Different methods to construct the results of the weight assignment of the complexity evaluation index
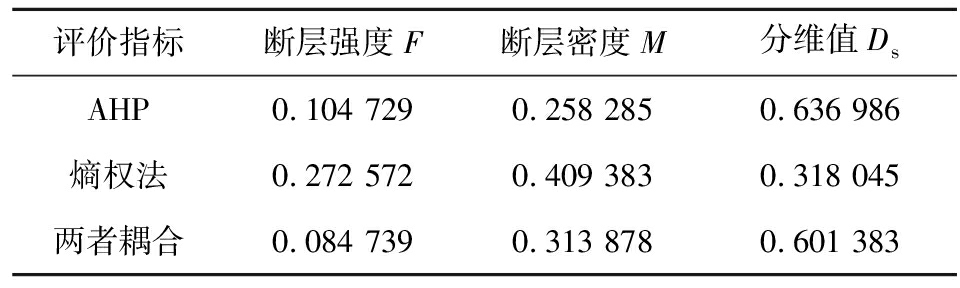
评价指标断层强度F断层密度M分维值DsAHP0.104 7290.258 2850.636 986熵权法0.272 5720.409 3830.318 045两者耦合0.084 7390.313 8780.601 383
3.2 矿井构造复杂程度定量评价
将断裂分维值Ds、断层强度指数F、断层密度M的评价指标归一化后的数据导入ArcGIS中,建立出归一化专题图。再将权重值分别赋予3个评价指标,应用ArcGIS对各评价指标的归一化专题图进行融合计算,得到矿井构造复杂程度定量评价模型:
![]() 739B1+0.313 878B2+0.601 383B3
739B1+0.313 878B2+0.601 383B3
式中:Qt为评价指数;Bj为第j个评价指标的归一化值。
根据矿井构造复杂程度定量评价模型,通过对Qt进行统计分析,运用Natural Breaks(Jenks)(自然间断分级法)进行分级,确定分级阈值,见表8。Qt的值和矿井构造复杂程度的关系,Qt越大,构造越复杂。
表8 矿井构造复杂程度分级
Table 8 Classification of mine structure complexity

Qt值构造复杂程度Qt>0.5复杂0.3
研究区被划分成4个区域,依据的是分级阈值,4个区域分别为将复杂构造区、较复杂构造区、中等复杂构造区和简单构造区,如图9所示。研究区的中西部地段为复杂构造区;中部地段为较复杂构造区;DF2断层以北区域为中等复杂构造区;DF2断层以南区域、DF1断层和DF3断层之间的区域为简单构造区。

图9 研究区构造复杂程度分区
Fig.9 Structural complexity division of study area
4 结 论
1)选取影响构造复杂程度的分析评判的3个主控因素:断层分维值、断层强度指数、断层密度,利用AHP与熵权法两者耦合的方法得到矿井构造复杂程度定量评价模型。
2)利用研究得出的构造复杂程度定量评价模型对整个研究区构造复杂程度进行了预测评价,将井田范围内的复杂程度分为4个等级区域,包括复杂构造区、较复杂构造区、中等构造区、简单构造区。
3)研究区复杂构造区主要集中在矿井中部偏西的区域,较复杂构造区主要集中在矿井中部;中等构造区主要分布在矿井DF2断层以北区域简单构造区主要分布在矿井DF2断层以南区域、DF1断层和DF3断层之间的区域。
[1] 李 飞, 杨滨滨, 张金陵, 等. 矿井断层构造复杂程度的GIS与熵值耦合评价研究[J].中国煤炭地质, 2014, 26(8):60-63.
LI Fei,YANG Binbin,ZHANG Jinling,et al. GIS and entropy coupling evaluation on mine fault structural complexity[J]. Coal Geology of China, 2014, 26(8):60-63.
[2] 施龙青,刘 捷,邱 梅,等.断层定量化在突水危险性评中的应用[J].中国科技论文,2020,15(1):100-104,130.
SHI Longqing,LIU Jie,QIU Mei,et al. Application of fault quantification in risk assessment of water inrush[J].China Ciencepaper,2020,15(1):100-104,130.
[3] 徐 慧,牟 义,牛 超.矿井涌水量渗透系数构造分形优化研究[J].煤炭科学技术,2021,49(10):228-232.
XU Hui,MU Yi,NIU Chao.Study on optimization of permeability coefficient of structural fractal for mine water inflow[J].Coal Science and Technology,2021,49(10):228-232.
[4] 魏大勇,王 飞,许进鹏,等.基于分形与模糊综合评价法的矿井突水危险性评价[J].煤矿安全,2013,44(8):184-186.
WEI Dayong, WANG Fei, XU Jinpeng,et al. Risk evaluation of mine water inrush based on the fractal and fuzzy comprehensive evaluation method[J]. Safety in Coal Mines, 2013, 44(8): 184-186.
[5] 尹尚先,徐 维,尹慧超,等. 深部开采底板厚隔水层突水危险性评价方法研究[J]. 煤炭科学技术, 2020, 48(1): 83-89.
YIN Shangxian, XU Wei, YIN Huichao, et al. Study on risk assessment method of water inrush from thick floor aquifuge in deep mining[J]. Coal Science and Technology, 2020, 48(1): 83-89.
[6] 张晓亮.熵权耦合层次分析赋权在煤层底板突水评价中的应用[J].煤田地质与勘探,2017,45(3):91-95.
ZHANG Xiaoliang. Application of entropy weight method and analytic hierarchy process in evaluation of water inrush from coal seam floor[J]. Coal Geology & Exploration, 2017,45(3):91-95.
[7] 刘令生.基于分形理论的矿区构造定量分析及评价[J].华北科技学院学报,2018,15(3):1-9.
LIU Lingsheng. Research on quantitative evaluation of structural complexity of eastern flank of Kaiping syncline[J].Journal of North China Institute of Science and Technology,2018,15(3):1-9.
[8] 姚振兴,严家平,沈掌旺,等. 涡阳矿区花沟西井田10煤层断裂网络复杂程度定量评价[J].中国煤炭地质,2012,24(6):26-29.
YAO Zhenxing,YAN Jiaping,SHEN Zhangwang,et al. Quantitative Assessment of No.10 coal Seam faulting network complexity in huagouxi minefield, guoyang mining Area[J].Coal Geology of China,2012,24(6):26-29.
[9] 李新凤,魏久传,隋岩刚.构造分形在砂岩含水层富水性预测中的应用[J].中国煤炭地质,2013,25(3):30-34.
LI Xinfeng, WEI Jiuchuan, SUI Yangang. Application of structure fractal in sandstone aquifer water yield property prediction[J]. Coal Geology of China, 2013, 25(3):30-34.
[10] 邱 梅,施龙青,滕 超,等.构造预测与定量评价模型的构建及应用[J].煤矿安全,2013,44(9):207-210.
QIU Mei, SHI Longqing,TENG Chao,et al. Construction and application of structure forecast of quantitative evaluation model[J]. Safety in Coal Mines, 2013,44(9):207-210.
[11] 李小明,邵小朋,连会青.基于模糊综合评判法的地质构造复杂程度评价:以许厂煤矿330采区为例[J].中国煤炭地质,2019,31(3):6-11.
LI Xiaoming,SHAO Xiaopeng,LIAN Huiqing. Geological structural complexity assessment based on fuzzy comprehensive assessment method:a case study of Xuchang coalmine No.330 winning district[J].Coal Geology of China, 2019, 31(3): 6-11.
[12] 徐文军,张莎莎,吴财芳,等.基于层次分析法的煤储层构造复杂程度定量评价[J].河南理工大学学报(自然科学版),2019,38(2):20-26.
XU Wenjun, ZHANG Shasha, WU Caifang, et al. Quantitative assessment of structure complexity of coal reservoir based on analytical hierarchy process[J].Journal of Henan Polytechnic University (Natural Science),2019,38(2):20-26.
[13] 方家虎,李 志,张 洋,等.芦岭煤矿8煤层地质构造复杂程度综合评价[J].煤田地质与勘探,2016,44(1):22-26,30.
FANG Jiahu, LI Zhi, ZHANG Yang,et al. Comprehensive evaluation of geological structure complexity of 8th seam in Luling mine[J]. Coal Geology & Exploration, 2016, 44(1):22-26,30.
[14] 何松霖,刘 勇,康向涛,等.盘江矿区煤系地质构造复杂程度评价研究[J].煤炭科学技术,2017,45(6): 60,196-200.
HE Songlin,LIU Yong,KANG Xiangtao,et al. Research on evaluation of complexity of geological structure of coal measures in Panjiang Mining Area[J].Coal Science and Technology,2017,45(6): 60,196-200.
[15] 张小东,张 硕,孙庆宇,等. 基于AHP和模糊数学评价地质构造对煤层气产能的影响[J].煤炭学报,2017, 42(9):2385-2392.
ZHANG Xiaodong,ZHANG Shuo,SUN Qingyu,et al. Evaluating the influence of geological structure to CBM productivity based on AHP and fuzzy mathematics[J]. Journal of China Coal Society,2017, 42(9):2385-2392.
[16] 刘 伟,吴基文,胡 儒,等.矿井构造复杂程度定量评价与涌(突)水耦合分析[J].工矿自动化,2019,45(12):17-22.
LIU Wei,WU Jiwen,HU Ru,et al. Quantitative evaluation of mine structure complexity and its coupling analysis with water bursting[J].Industry and Mine Automation, 2019,45(12):17-22.
[17] 李 静,刘 晨,刘惠民,等.复杂断层构造区地应力分布规律及其影响因素[J].中国矿业大学学报,2021,50(1):123-137.
LI Jing,LIU Chen,LIU Huimin,et al.Distribution and influencing factors of in-situ stress in complex fault tectonic region[J].Journal of China University of Mining & Technology,2021,50(1):123-137.
[18] 尚天成,高彬彬,李翔鹏,等. 基于层次分析法和熵权法的城市土地集约利用评价[J].电子科技大学学报(社科版),2009,11(6):6-9.
SHANG Tiancheng,GAO Binbin,LI Xiangpeng, et al.Urban land intensive utilization evaluation based on AHP and entropy method[J].Journal of UESTC (Social Sciences Edition) 2009,11(6):6-9.
[19] 向文英,杨 静,张 雪. 模糊综合评价法的改进及其在水库水质评价中的应用[J]. 安全与环境学报,2015,15(6): 344-348.
XIANG Wenying, YANG Jing, ZHANG Xue. Improvement of fuzzy comprehensive evaluation method and its application to the evaluation of reservoir water quality[J].Journal of Safety and Environment,2015,15(6): 344-348.
[20] 王任一,巨亚明,石家骧.基于熵权系数与DTOPSIS集成油田生产能耗评价研究[J].国土资源科技管理,2005(2):51-53.
WANG Renyi,JU Yaming,SHI Jiaxiang.A study of energy consumption evaluation of integrated oil field based on entropy weight coefficient and dtopsis[J]. Scientific and Technological Management of Land and Rsources, 2005(2):51-53.
[21] 宫 博,许开立,李德顺. 基于熵权-属性识别模型的地表水质量评价[J]. 环境科学导刊,2011,30(6):74-77.
GONG Bo,XU Kaili,LI Deshun. Assessment of the surface water quality based on entropy weight of attribute recognition model[J]. Environmental Science Survey,2011,30(6):74-77.
[22] 张晓亮.熵权耦合层次分析赋权在煤层底板突水评价中的应用[J].煤田地质与勘探,2017,45(3):91-95.
ZHANG Xiaoliang. Application of entropy weight method and analytic hierarchy process in evaluation of water inrush from coal seam floor[J]. Coal Geology & Exploration, 2017,45(3):91-95.
[23] 唐李斌,吴基文,毕尧山,等.基于AHP-熵权法耦合的含水层富水性评价研究[J].中国矿业,2020,29(12):147-152.
TANG Libin,WU Jiwen,BI Yaoshan,et al. Evaluation of aquifer water abundance based on AHP-entropy weight method[J].China Mining Magazine, 2020,29(12):147-152.
[24] 侯恩科,纪卓辰,车晓阳,等.基于改进AHP和熵权法耦合的风化基岩富水性预测方法[J].煤炭学报,2019,44(10):3164-3173.
HOU Enke,JI Zhuochen,CHE Xiaoyang,et al. Water abundance prediction method of weathered bedrock based on improved AHP and the entropy weight method[J].Journal of China Coal Society, 2019, 44(10): 3164-3173.
[25] ZENG Y, WU, Q, LIU, S. et al. Evaluation of a coal seam roof water inrush: case study in the Wangjialing Coal Mine, China[J]. Mine Water and the Environment,2018,37:174-184.
