0 引 言
智慧矿山等数字化理念的提出,对可更直观、准确的展示地理实体三维空间数据的需求越来越多。在地学领域,自1980年以来众多专家建立了多种实体模型来模拟地质结构,主要包括基于面元的表面模型和基于体元的实体模型,其中表面模型能够快速表达物体外部结构,但该方法不能体现地质体内部特征,无法实现真正的地质体真三维重建[1-2]。而体元模型恰好弥补这一不足,该模型侧重于表示三维地质体内部整体或边界,比如对于矿体和地质体的各地层的表示,是借助三维空间的真三维实体的展示,常见的体元模型有四面体,六面体。利用不规则四面体描述的地质体,在层位面可以更加精确,内部结构的刻画也较为精细,对比之下六面体网格对细节的刻画不够精细[3-4]。
对于四面体剖分算法使用较多的是Delaunay四面体剖分,国内外学者对此做了大量研究。KARASICK等[5]对三维四面体网格剖分的可视化方法进行了研究。SI等[6]利用三维空间域的限定Delaunay四面体剖分,解决了限定边界难以恢复的问题。DEVILLERS等[7]将随机扰动的方法引入到三维四面体剖分中。BUCHIN等[8]提出一种高效的四面体剖分方法,该方法主要是对三维Delaunay的顶点进行删除,大大提高处理效率。LO[9]也在利用Delaunay四面体剖分对恢复边界的处理上进行算法研究[9],该学者是利用增加顶点的方法,从而做到边界边及面的恢复。国内专家学者在此领域有些许滞后,崔汉国等[10]利用动态修改和自动生成的算法,建立了另一种方式的三维空间的Delaunay四面体剖分。胡于进等[11]利用Delaunay的空外接圆准则,获得插入点的最佳位置改进了之前的算法。赵建军等[12]提出边界一致的Delaunay四面体稳定生成算法,避免了之前剖分算法中的不足。杨忱瑛等[13]也提出了一种新的三维限定Delaunay四面体剖分的算法。刘岩[14]改进了网格单元质量优化算法,提高了剖分四面体的质量。
以上诸多学者基于四面体重建已经做出多种探索,并取得一定成效,但对于地层,尤其断层等具体地质结构重建缺少具体实施方案。为解决地层模型内部属性表征问题,结合该模型体元结构简单、能有效描述拓扑关系、能够有效地实现插值运算、能快速进行几何和逻辑变换的特点,基于Tetgen四面体剖分算法库,探讨了四面体模型下的地质层和断层的三维重建研究。
1 四面体建模理论基础
根据四面体在地质层内部建模的良好特性,利用Tetgen四面体剖分算法库[15-19]实现了Delaunay三角剖分和Edelsbrunner以及Shah的随机增量翻转算法,并且生成的自适应四面体网格质量较高,在有限元或有限体积数值计算时有着良好适应性。
假设存在一个三维区域A,借助诸多四面体尽可能地准确描述该区域,当然该区域内的四面体形状是大小不一样的。点集W中存在2个点可见的p、q点,构建约束平面f,构建条件为点p、q两点分别位于平面f的上下两边,p、q间的线段交叉于平面f, 并且两顶点不可见。由此条件下众多顶点构成点集W,约束Delaunay四面体的顶点都处于点集W中。借助四面体描述区域形态的方式称为约束Delaunay四面体剖分。
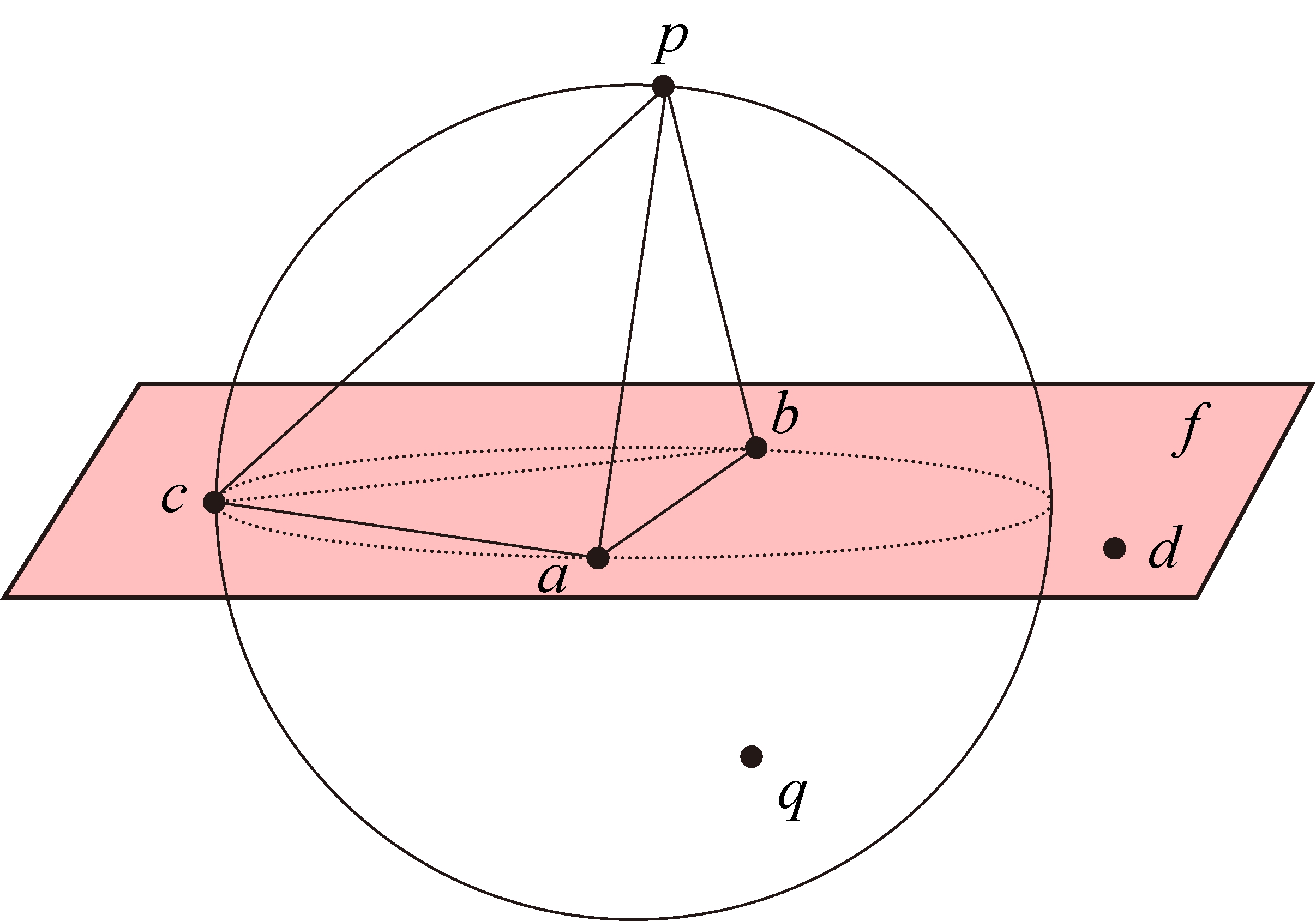
图1 约束Delaunay四面体剖分
Fig.1 Constrained Delaunay tetrahedral meshing
Tetgen算法在构建四面体网格时,总能避免最小或最大二面角四面体出现。构建高质量四面体网格主要是源于多种条件的约束,比如三维顶点,约束段,不少于90°的输入角和小平面,等多个点线面控制条件。同时四面体网格的半径边缘比不大于2.0这一条件的约束下的网格基本能描述各种情况。通常,借助边界纵横比来判断网格划分的质量情况[20]。边界纵横比ηt是最大边的长度lmax与最小高度hmin的比值,即
(1)
边界纵横比和四面体网格质量成反比,越小的比值代表质量越高。
但Tetgen借助半径边缘比来控制网格质量情况,半径边缘比是由MILLER等[21]提出的网格控制准则。该准则是指控制一个四面体t只存在一个外接球条件下,分别获取四面体外接球的半径r以及四面体最短边的长度d。那么四面体的半径边缘比ρt是:
(2)
式中:θmin为四面体t的最小面角。
同样,半径边缘比和四面体网格质量成反比,较小的比值代表质量越高。
笔者是在Ubuntu系统下对Tetgen进行编译,并将该库命名为“Tetgen.a”。通过对该库的调用,实现了三维实体结构的网格划分。
2 四面体建模
2.1 基于Tetgen的地质建模
Tetgen算法库主要是根据已知的三维点集,重新构建点集的Delaunay四面体格网或者权重Delaunay四面体格网的过程。借助Tetgen算法库进行地层建模具体过程为:
1)根据钻孔数据以及CAD图获取地层数据,并建立表面不规则三角网,完成地层表面模型的重建。
2)由于Tetgen存在多种约束条件才能构建高质量四面体网格,因此输入数据需要预处理,进行有效性检查,对检查后的数据使用静态链接库Tetgen.a进行下一步处理,反之重复以上步骤。
3)Tetgen算法主要有4块内容:计算特殊点、得到跟踪边、生成表面网格生成,最后完成体剖分,在数据处理时利用Tetgen的核心算法库Tetgen.a完成四面体剖分。
4)根据实际情况选取合适的剖分参数,对模型剖分,最终得到完整的地质层四面体模型。
2.2 方法实现
该算法进行建模流程如图2所示。

图2 四面体建模流程
Fig.2 Flow chart of tetrahedron modeling
1)面模型建立。根据获取的巷道模型以及钻孔数据,首先完成单层和多层地层表面模型的建模并以*stl二进制格式保存,文件包含顶点,面片等信息。
2)模型初始检验。Tetgen以分线段复杂体(PLC)[20]来描述三维几何体对象,对于输入的模型需要判定是否满足该规则,地层模型的初始检验主要是避免模型相交以及非闭合等问题,无法进行四面体剖分。
以./tetgen-ddxxf.stl命令调用库文件,首先是对顶点进行分析。然后检查2个单曲面的地层模型的自相交情况,一般来说自相交会出现共面相交三角形以及异面相交三角形2种情况。无论哪种情况三角形都要重新处理,并基于交点形成2个同顶点三角形,从而通过Tetgen对输入模型的相交性检查。
3)四面体网格构建。我们需要用到的参数为tetgenbehavior *b, tetgenio *in, tetgenio *out, tetgenio *addin这4个,这4个参数的含义分别指代限定剖分选项参数结构、输入网格结构,输出剖分结构,附加点集输入结构,限定剖分其实就是输入Point+Mesh,输出TetraMesh的过程。
4)模型的输出。运用./tetgen-q*.stl命令对模型进行四面体剖分,依次运行顶点、面片读取,顶点,格网优化,重建等过程,完成四面体模型重建。最终输出模型的点集文件、四面体列表文件、三角面片文件、四面体格网的边界列表文件、PLC专用的表面格网文件。
3 试验验证
以某煤矿扫描数据为例,验证算法的可行性,采用三维激光扫描仪获取巷道点云数据,根据钻孔资料及CAD图纸数据获取地质层数据。
3.1 巷道建模
利用三维激光扫描仪采集了海量的巷道点云数据,在配套的数据处理工具中完成点云预处理。随后通过配准、去噪、抽稀等操作获取可用于建模的巷道点云,预处理后的点云如图3所示。

图3 巷道整体点云
Fig.3 Tunnel overall point cloud
以构网拟合的方式对点云建模,得到巷道初始模型,为使模型更加精细对模型进行孔洞修补,打磨及优化,具体模型效果如图4所示。

图4 巷道模型效果
Fig.4 Effect of tunnel model after processing
3.2 地质层实体建模
结合钻孔数据以及CAD信息完成地层模型的构建。主要分为钻孔数据处理,面模型构建以及体元模型构建等步骤。
1)钻孔数据处理。利用研究区域工程地质平面图,采用人工方式,提取钻孔详细数据,在对提取的数据进行解译后参与后期三维地质模型的构建。
2)地层面模型构建。根据钻孔数据并将岩层数据进行整理,借助建模软件以人工提取地质信息的方式确定地层的大致范围;然后勾绘出矢量线模拟地质形态确定单层地层面片;将单层面片按照高度进行拉伸完成各地层模型;最后建立地层模型的表面模型,并将不同岩层赋予不同的纹理材质,为效果展示做注释,地层模型如图5所示。

图5 地层模型
Fig.5 Stratigraphic model
结合巷道模型与地层模型进行布尔运算,采用曲面相交的方法获取地层轮廓形状。根据钻孔数据以及巷道数据进行多种约束进行地层建模,具体效果如图6所示。

图6 约束轮廓后的地层模型
Fig.6 Strata model after constrained profile
3)体元地层模型构建。将获取的地层表面模型采用第2节中的四面体剖分算法进行体元化的地层模型重建。以./tetgen-pq1.2Va1zdc.stl命令对地层模型进行重建,其重建效果如图7所示。

图7 地层四面体模型
Fig.7 Strata tetrahedron model
3.3 断层结构的表达
参照地层模型整体构建方法,以局部法建立断层模型。具体步骤如下:
1)根据各类钻孔及其他资料大致整理断层位置及分界面信息;并根据断层属性对于断层每部分采用分片处理建立单层模型;最后采用人工编辑的方式形成无拓扑关系的地层层面。从而确定基本的空间形态,最终构建的表面模型如图8所示。
2)根据构造出的地层表面模型,采用四面体剖分的方法完成含断层结构的地层剖分,由于采用局部法构造的表面模型,需要尤其注意多地层模型的相交性。首先对模型初始剖分,并根据模型效果选取合适的剖分参数,为保持格网图元优良性,增加格网顶点并增加半径约束条件,使得外接圆半径和边的比率不超过1.2。模型结果如图9所示。

图8 断层面模型
Fig.8 Fault plane model

图9 断层体元模型
Fig.9 Fault voxel model
4 结 论
1)针对地层模型缺少内部属性表达的问题,研究了Tetgen算法库在地质模型三维重建中的应用,结合Tetgen算法库便于完成网格细分、角点重组的特性提出了一种体元结构下的地质模型重建方法。
2)根据钻孔等数据完成地层面模型的重建,为判断模型相交以及非闭合状态借助静态库文件完成模型初始检验。并根据实际情况,为了尽可能展现实体信息便于内部结构表达,进行优化剖分参数,最终获取最优的地层四面体模型。
3)针对断层特殊地质结构复杂且对于以面模型来表达该构造缺乏内部结构的特点,采用局部法完成断层部分面模型的构建,并多次调整单层面片后确保各层之间无交叉以通过初始检验,借助四面体良好的空间拓展性,用合适的四面体剖分参数,完成了断层结构的体元建模。
[1] 王敬谋.三维地质建模及岩层自动划分与对比技术研究[D].淮南:安徽理工大学,2018.
WANG Jingmou. Research on 3D geological modeling and automatic division and comparison of rock formations [D].Huainan:Anhui University of Science and Technology, 2018.
[2] 程朋根,文 红.三维空间数据建模及算法[M].北京:国防工业出版社,2011:25-26.
CHENG Penggen, WEN Hong. Three-dimensional spatial data modeling and algorithm [M]. Beijing:National Defense Industry Press, 2011:25-26.
[3] 詹学才.三维地质模型四面体剖分及优化研究[D].成都:成都理工大学,2019.
ZHAN Xuecai. Research on trihedral division and optimization of 3D geological model [D].Chengdu:Chengdu University of Technology, 2019.
[4] 周龙泉.非结构化有限元网格生成方法及其应用研究[D].青岛:山东科技大学,2019.
ZHOU Longquan. Unstructured finite element mesh generation method and its application research [D]. Qingdao:Shandong University of Science and Technology, 2019.
[5] KARASICK M S, LIEBER D, NACKMAN L R, et al. Visualization of three-dimensional delaunay meshes[J]. Algorithmica, 1997, 19(1):114-128.
[6] HANG Si. On refinement of constrained delaunay[C]// Proceedings of the 15th International Meshing Roundtable. Springer Berlin Heidelberg, 2006.
[7] OLIVIER Devillers,MONIQUE Teillaud. Perturbations for delaun-y and weighted delaunay 3D triangulations[J]. Computational Geometry:Theory and Applications,2010,44(3):160-168.
[8] BUCHIN K,DEVILLERS O, MULZER W, et al. Vertex deletion for 3D delaunay triangulations[C]// European Symposium on Algorithms. Springer, Berlin, Heidelberg, 2013.
[9] LO S H. Delaunay triangulation of non-uniform point distributions by means of multi-grid insertion[J]. Finite Elements in Analysis and Design, 2013, 63(4):8-22.
[10] 崔汉国,胡瑞安,金瑞峰,等.三维点集Delaunay三角剖分的自动生成与修改算法[J].工程图学学报,1995(2):1-7.
CUI Hanguo, HU Ruian, JIN Ruifeng,et al. Automatic generation and modification algorithm of Delaunay triangulation of 3D point set [J]. Journal of Engineering Graphics, 1995(2):1-7
[11] 胡于进,赵虎跃,赵建军.基于Delaunay准则的三维网格自动插点算法[J].华中理工大学学报,2000,28(5):7-9.
HU Yujin, ZHAO Huyue, ZHAO Jianjun. Algorithm of automatic insertion of 3D mesh based on Delaunay criterion [J]. Journal of Huazhong University of technology, 2000,28(5):7-9.
[12] 赵建军,王启付.边界一致的Delaunay四面体网格稳定生成算法[J].机械工程学报,2004,40(6):100-106.
ZHAO Jianjun, WANG Qifu. Delaunay tetrahedral mesh generation algorithm with uniform boundary [J]. Journal of Mechanical Engineering, 2004,40(6):100-106
[13] 杨忱瑛,陈文亮.三维限定Delaunay四面体网格划分的算法[J].中国制造业信息化,2009,38(7):49-50,54.
YANG Chenying, CHEN Wenliang. Algorithm of three-dimensional Delaunay tetrahedral mesh generation [J]. China manufacturing informatization, 2009,38(7):49-50,54.
[14] 刘 岩. 高效可靠的三维约束Delaunay四面体有限元网格生成算法[D].大连:大连理工大学,2010.
LIU Yan. Efficient and reliable 3D constrained Delaunay tetrahedral finite element mesh generation algorithm [D].Dalian:Dalian University of Technology, 2010.
[15] 段红俊.连续刚构桥三维有限元参数化建模研究[D].重庆:重庆交通大学,2016.
DUAN Hongjun. Three-dimensional finite element parametric modeling of continuous rigid frame bridges [D].Chongqing:Chongqing Jiaotong University, 2016.
[16] 王家林,段红俊.基于Tetgen的箱梁三维四面体网格自动划分分析[J].重庆交通大学学报(自然科学版),2016,35(5):1-4.
WANG Jialin, DUAN Hongjun. Analysis of 3D tetrahedral mesh automatic generation based on Tetgen [J]. Journal of Chongqing Jiaotong University (Natural Science Edition), 2016, 35(5):1-4.
[17] 吴 广.三维地质建模中的关键技术研究[D].成都:成都理工大学,2015.
WU Guang. Research on key technologies in 3D geological modeling [D].Chengdu:Chengdu University of Technology, 2015.
[18] 荆永滨,王李管,贾明涛,等.基于Tetgen的复杂FLAC~(3D)模型可视化建模方法[J].岩土力学,2010,31(8):2655-2660.
JING Yongbin, WANG Liguan, JIA Mingtao,et al. Visual modeling method of complex FLAC ~ (3D) model based on Tetgen [J]. Rock and Soil Mechanics, 2010,31(8):2655-2660.
[19] SI Hang. Tetgena delaunay-based quality tetrahedral mesh generator[J]. ACM Transactions on Mathematical Software,2015,41(2):1-36.
[20] 郭 飞,余淑娟,李 想,等.特征约束的四面体生成方法与案例分析[J].地球信息科学学报,2012,14(5):555-561.
GUO Fei, YU Shujuan, LI Xiang,et al. Feature-constrained tetrahedron generation method and case analysis [J]. Journal of Earth Information Science, 2012,14(5):555-561.
[21] MILLER G L,TALMOR D,TENG S H, et al. A Delaunay based numerical method for three dimensions: generation, formulation, and partition[C]//In Proceedings of the twenty-seventh annual ACM symposium on Theory of computing (STOC '95)1995:683-692.
