0 引 言
矿井移动通信、人员及车辆定位、无线摄像机、无线传感器等无线通信技术和装备,已在煤矿井下推广应用,在煤矿安全生产和煤矿智能化中发挥着重要作用[1-2]。矿井电磁波传输和能量分布与自由空间不同,受巷道断面形状和大小、巷道弯曲和分支、通行车辆等影响较大,地面开放空间的电磁波传播理论不能直接用于矿井巷道内。为保证车辆和行人正常通行,无线通信基站和固定无线通信设备(如无线摄像机和无线传感器等)天线一般安装在巷帮附近。为了提高矿井无线信号覆盖范围,提升矿井无线通信质量,减少井下无线通信基站数量,需要研究无线通信基站天线和固定无线通信设备天线安装位置对矿井电磁波传播特性的影响。
目前,矿井电磁波传播分析方法主要有现场实测法[2-5]、波导模态法(Waveguide Modal)[6-8]、几何光学法(Geometrical Optical, GO)[9-11],时域有限差分法(Finite-Difference Time-Domain,FDTD)等[12-15]。张跃平等[3]用900 MHz无线电波在矿井巷道断面中心区域测量,根据接收信号功率用线性回归分析方法,把巷道内传播区域分为快速衰减和缓慢衰减两部分,但没有给出计算公式和经验公式。文献[3-5]在不同类型巷道内用450~900 MHz、2.4 G Hz电磁波开展测量试验,给出不同巷道断面面积、巷道弯曲度、电磁波极化类型等条件下电磁波随距离变化的衰减规律,但测量时发射天线和接收天线都在巷道断面中心。EMSLIE等[6]研究200~4 000 MHz范围内的矿井电磁波,该波段的波长远小于巷道尺寸,因此把巷道等效为相对介电常数在5~10之间的一个有耗的超大矩形波导,推导出发射天线在巷道内不同位置的插入损耗公式,但发射天线在贴近巷帮时该公式计算出的插入损耗趋向于无穷大,与事实不符。ZHOU等[8]以波导和菲涅尔反射理论为基础,计算出矩形介质壁波导中电磁波的衰减常数的解析表达式,计算结果与巷道内的测量试验基本吻合,但是解析式只与巷道面积、距离以及巷道壁介电常数有关,并且测量试验同样在巷道断面中心区域,没有研究收发天线在巷道断面不同位置处的电磁波衰减规律。MAHMOUD等[9]把巷道等效为理想矩形波导,通过计算波导内从发射点到达接收点的有效射线和,首次用几何光学(Geometrical Optical,GO)和波导模推导电磁波的衰减模型;ZHOU等[11]基于波导模态法和射线追踪法(Ray Tracing, RT)研究了巷道壁面粗糙度对电磁波衰减的影响,证明可以用泊松求和公式将RT的解析式收敛到波导模态法的解析式,统一了RT和波导模态方法,但研究重点同样是收发天线在巷道断面中心区域时的电磁波传播特性。
综上所述,现有的众多矿井电磁波分析方法和测量试验主要用于研究发射天线和接收天线位于巷道断面中心及附近区域的电磁波传播特性,难以满足无线基站和固定无线通信设备等天线布置需求。FDTD作为一种全波分析方法,一次仿真可得到整个计算空间内电磁波信号的能量分布情况。张帆[13]用FDTD计算了矿井泄漏天线的辐射场,TAGUCHI等[14]用FDTD研究了住宅区内半封闭空间中地面反射、围墙厚度、高度对720 MHz电磁波传播特性的影响。针对矿井巷道这一封闭空间,也可以建立贴合实际的巷道模型,用FDTD方法研究电磁波在巷道内的传播特性。在FDTD巷道模型中用激励源模拟发射天线,其仿真结果本身就考虑了巷道内辐射波、反射波、透射波之间的相互影响,以及多径传播和巷道壁电磁特性对电磁波传播特性的影响。笔者建立一个FDTD三维巷道模型,在该模型的基础上推导FDTD迭代方程;提出一种可变内阻电流激励源用于模拟巷道内的发射天线;在煤矿井下进行测量试验以验证巷道模型和激励源的可靠性;研究收发天线在巷道断面内不同位置处的电磁波传播特性,为煤矿井下无线通信系统和设备规划、天线安装提供指导。
1 FDTD建模
1.1 基本原理
时域有限差分(Finite-Difference Time-Domain, FDTD)是一种全波时域数值计算方法。该方法把麦克斯韦微分方程组中的2个旋度方程从时间上离散并转化为一组差分方程,在时间和空间上对电磁场各分量交叉采样,按照时间步推算出整个计算空间内电磁场能量分布状态[16-18]。实际应用时需要先规划计算空间,设计一个与发射天线性能基本一致的激励源,通过多个时间步迭代最终仿真出整个计算空间的电磁场强度。Yee网格[19]可以准确描述FDTD方法的空间离散方式,图1中给出了一个完整Yee网格Cell(i,j,k)及其沿x、y、z方向上的电场分量Ex(i,j,k)、Ey(i,j,k)和Ez(i,j,k),磁场分量Hx(i,j,k)、Hy(i,j,k) 和Hz(i,j,k)。蓝色箭头表示网格Cell(i,j,k)的电场分量方向,红色箭头表示Cell(i,j,k)的磁场分量方向,其他网格的电磁场分量都用黑色箭头表示。从图1可知,每个面中心的磁场矢量围绕4个电场矢量,每个棱上的电场矢量同样围绕4个磁场矢量;同样也可以把电场矢量放在面中心,磁场矢量放在棱上,这两种空间分布都符合安培环路定律和法拉第电磁感应定律。

图1 Yee网格电磁场节点空间分布
Fig.1 Electromagnetic field node spatial distribution of the Yee cell
根据图1中电磁场节点空间分布情况,设定磁场分量位于Yee网格面上,电场分量在Yee网格棱上。在空间对电场和磁场离散后,部分电场分量和磁场分量的空间坐标和Yee网格坐标会存在半网格空间步长偏移,在求解贴近巷帮电场时需要考虑该电场的实际空间坐标。对于网格Cell(i,j,k)上的电场分量Ex(i,j,k),实际空间坐标为Ex(i+1/2,j,k),向x方向移动半个空间步长。磁场分量Hx(i,j,k)的实际空间坐标为Hx(i,j+1/2,k+1/2),向y和z方向移动半个空间步长。网格Cell(i,j,k)的各电磁场分量实际空间坐标分布见表1。同时约定电场在整数时间步采样,磁场在半整数时间步采样。
表1 电磁场分量实际空间坐标分布
Table 1 Real spatial coordinate distribution of the electromagnetic field components

电磁分量x轴y轴z轴Exi+1/2jkEyij+1/2kEzijk+1/2Hxij+1/2k+1/2Hyi+1/2jk+1/2Hzi+1/2j+1/2k
1.2 巷道建模
用FDTD方法研究巷道电磁波传播特性,首先需要建立一个和实际巷道近似的仿真巷道模型。根据文献[7]可以把拱形和马蹄形巷道等效为一个断面面积相同的矩形巷道,在此创建一个矩形巷道模型,巷道宽为x、巷道高为y、巷道长为z,内部组成结构如图2所示。
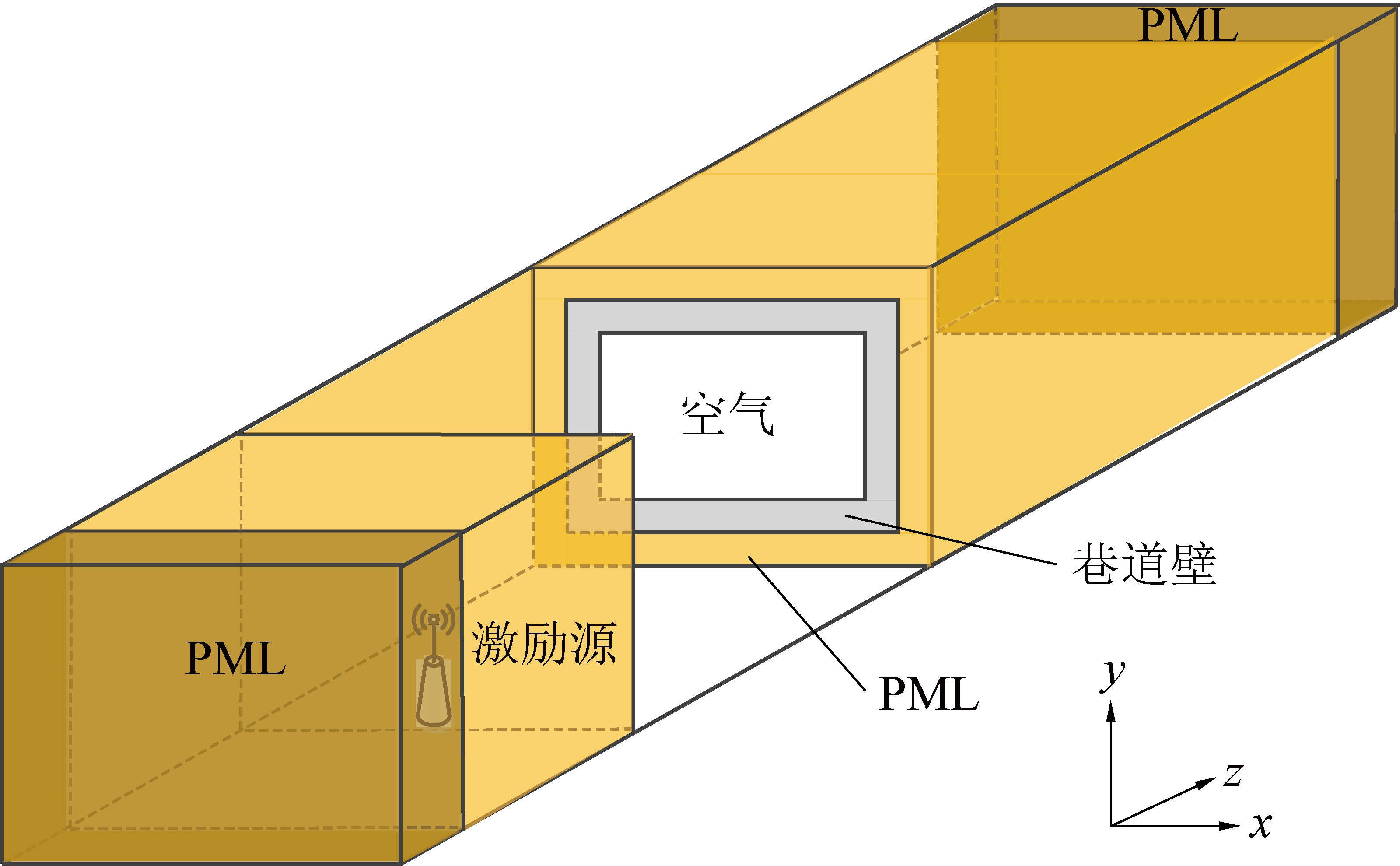
图2 巷道仿真模型
Fig.2 The simulation model of the tunnel
巷道模型主要由空气介质、巷道壁和完全匹配层(Perfectly Matched Layer,PML)3部分组成。第1部分为空气介质,位于巷道中心区域,激励源和接收点均位于该区域,激励源在该区域不同位置时所引起的电磁波传播特性是本文研究的重点,其结果可以用来指导无线基站和无线摄像机等天线在巷道内的安装位置,以取得最远通信距离和最佳通信效果。第2部分为巷道壁,该区域为有耗介质,电磁波从空气传播到该区域时会在交界面上发生反射和透射,反射波会再次进入到巷道空气区域形成多径传播,透射波则进入到巷道壁外侧的PML内。第3部分PML为整个巷道模型的最外层,包裹整个巷道壁,从空气介质进入到巷道壁的透射波在此区域全部被吸收,与实际巷道电磁波的传播环境保持一致,可以防止透射波再次进入到空气介质内带入新的计算误差。在PML区域采用坐标伸缩完全匹配层[20]吸收来自巷道壁各个方向的透射波,其优点是PML中的电磁参数与仿真区域完全一致,保证从空气中透射到巷道壁中的透射波到达PML区域时不存在反射波。
1.3 迭代方程
根据麦克斯韦微分方程组中的安培环路定律和法拉第电磁感应定律,可以推导出FDTD基本迭代方程。推导出基本迭代方程后,根据1.2节建立的巷道仿真模型,空气介质、巷道壁和PML三个被Yee网格离散化的区域需要用各自区域的电磁参数,代替基本迭代方程中的电磁参数,实现对目标巷道内电磁波的仿真过程。安培环路定律和法拉第电磁感应定律的微分形式为:
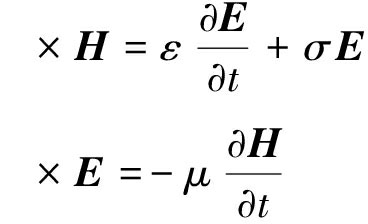
(1)
式中:∇为Hamiltonian算子;∂为偏导数符号;E为电场强度矢量;H为磁场强度矢量;ε为电磁波传输介质的介电常数;σ为传输介质的电导率;μ为传输介质的磁导率;t为时间。
把式(1)中2个方程的电场和磁场矢量在直角坐标系下用x、y、z三个方向的标量形式表示,并把旋度方程展开可得:

(2)
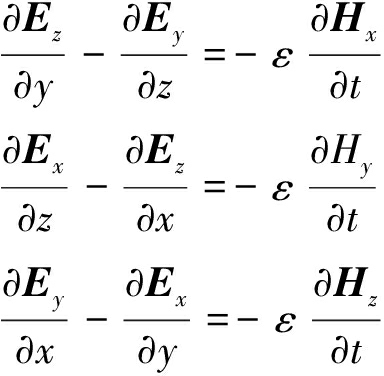
(3)
设网格x、y、z 3个方向的空间步长分别为Δx、Δy、Δz,把式(2)和式(3)中对3个方向空间的偏导和对时间的偏导用中心差分近似表示,整理后可得一个Yee网格内第n个时间步和n+1时间步3个方向电场分量的迭代方程:
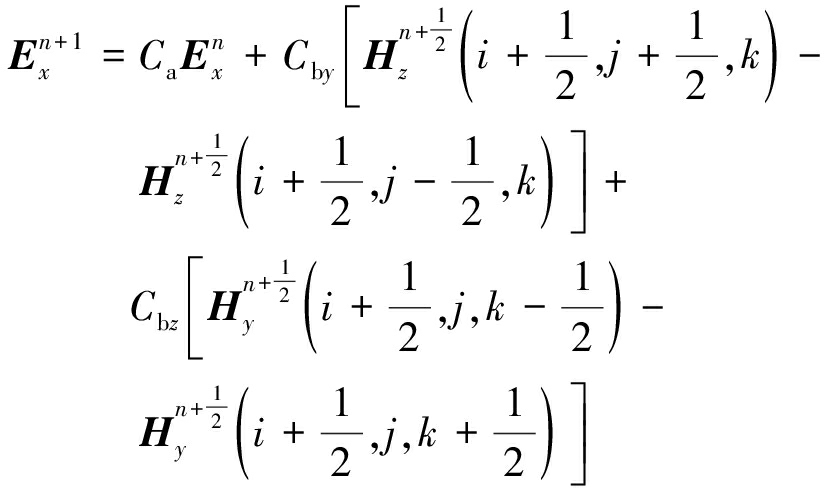
(4)
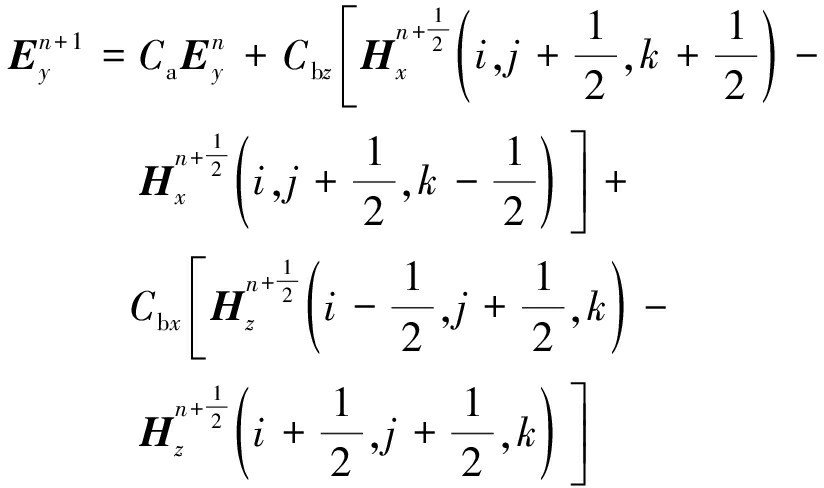
(5)

(6)
其中,系数![]() 为整数,表示FDTD迭代中的时间步。电场在整数时刻采样,磁场在半整数时刻采样。根据第n时间步的电场分量和第n+1/2时间步的磁场分量就可以求出第n+1时间步的电场分量。
为整数,表示FDTD迭代中的时间步。电场在整数时刻采样,磁场在半整数时刻采样。根据第n时间步的电场分量和第n+1/2时间步的磁场分量就可以求出第n+1时间步的电场分量。
同理磁场分量迭代方程为

(7)
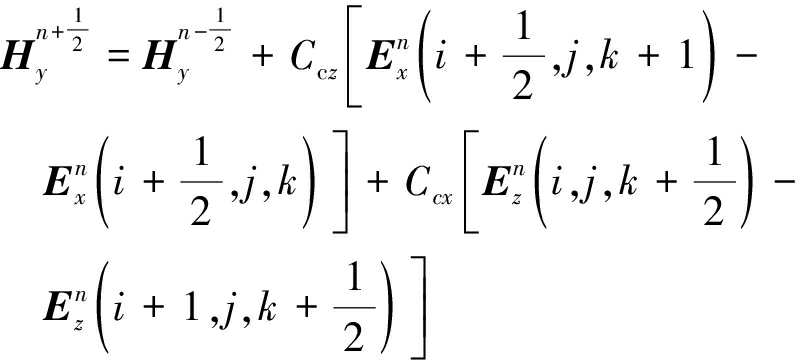
(8)

(9)
其中,![]() 同理,根据第n-1/2时间步的磁场分量和第n时间步的电场分量可以求出第n+1/2时间步的磁场分量。
同理,根据第n-1/2时间步的磁场分量和第n时间步的电场分量可以求出第n+1/2时间步的磁场分量。
巷道模型把待求解巷道划分成多个Yee网格组成的计算空间,模型中不同区域使用各自的电磁参数代替式(4)—式(9)的通用参数,经过多个时间步迭代后,即可求得整个巷道内的电磁场分布情况。
为防止仿真结果发散,仿真时的时间步长和空间步长需要满足CFL(Courant-Friedrichs-Lewy)稳定性条件,在三维空间内需满足[21]:
(10)
若使用均匀网格且3个方向的空间步长均为δ,则式(10)可简化为
(11)
1.4 可变内阻激励源
FDTD方法需要一个激励源把电磁波能量耦合到整个FDTD计算空间,设计一个好的激励源模型可以提高FDTD方法计算巷道内电磁波传播特性的准确性,保证电磁波频率工作在预定频带、减少因空间离散带来的感应电磁场干扰,提高计算精度。常用的激励源有硬源(hard sources)和透明源(transparent sources)[22]。硬源对FDTD特定网格强制赋值,实现简单,但会受计算空间内的反射波和散射波干扰。通过修正FDTD迭代方程可以引入透明源,该激励源与不连续介质面产生的反射波之间不存在相互作用,消除了激励源和反射波、散射波的相互影响。
高频电流在天线周围产生时变电磁场,进而激发出电磁波信号,为用FDTD方法研究宽带标签天线的性能,文献[23]提出了一种RLC电压激励源。矿井下测量试验多使用全向鞭状天线[2-4, 7],根据鞭状天线结构及原理,在文献[23]电压源的基础上,提出了一种可变内阻的透明电流激励源,使其更加符合实际测量天线由时变电流激发电磁波信号的属性。该激励源可以计算空间离散后网格之间的感应电流,并将该感应电流作为附加源再次耦合到FDTD迭代方程中,减小因感应电流引起的计算误差,还可以调整需要仿真天线的内阻,提高仿真精度。可变内阻激励源的基本原理如图3所示。

图3 可变内阻激励源原理
Fig.3 The principle of variable internal resistance excitation source
图3中把激励源设置在网格Cell(i,j,k)和Cell(i,j+1,k)之间,Is为激励源电流,Rs为激励源内阻,Δx、Δy、Δz为Yee网格在x、y、z三个方向上的空间步长。电流源一旦开启,Cell(i,j,k)上会产生y方向感应电场Ey(i,j,k),因为在此方向上又存在长度为Δy的离散空间,故在Cell(i,j,k)和Cell(i,j+1,k)之间会产生感应电压ΔV,且满足:
(12)
可得Cell(i,j,k)和Cell(i,j+1,k)之间的总电流I为
(13)
在FDTD迭代方程中引入的激励源需要用电流密度表示,根据Yee网格xoz面的大小可把式(13)转换为电流密度Jsy为
(14)
把式(14)代入式(2)的第2项即可把电流源耦合到FDTD迭代方程中,即:
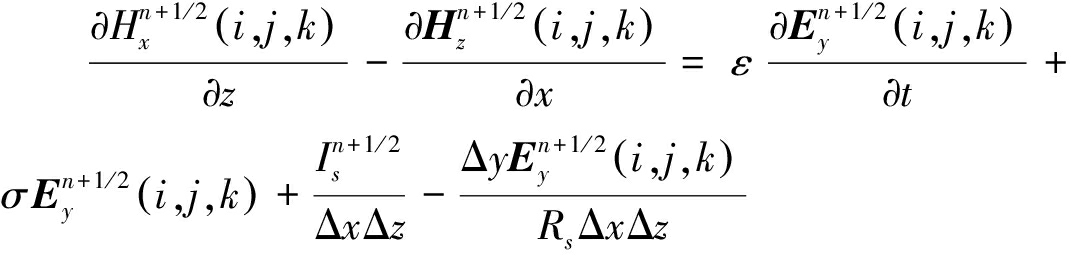
(15)
求出Hx对z的偏导数、Hz对x的偏导数,Ey对时间t的偏导数并用中心差分表示,整理后得到可变内阻电流激励源的FDTD迭代方程为
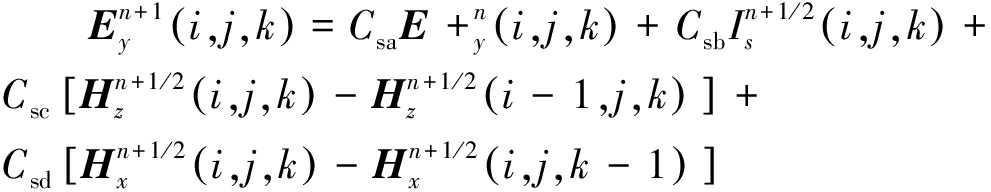
(16)
式(16)中的相关系数为
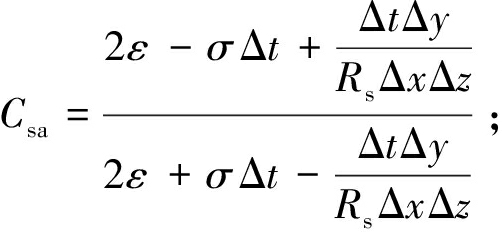
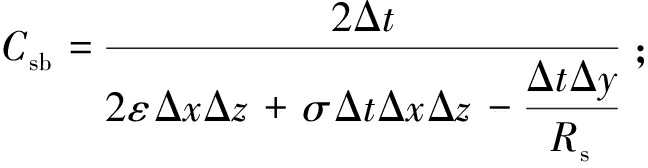
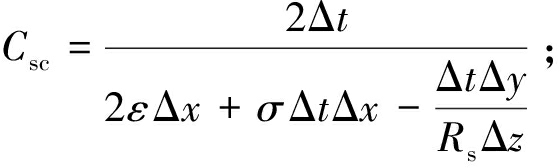
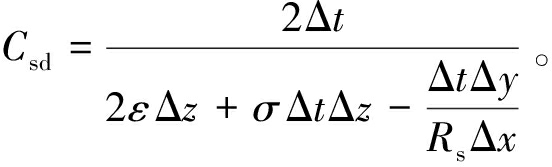
根据测量天线的体积和Yee网格空间步长大小,可以计算出天线所占网格数量。在离散后的巷道模型中设定Rs初值,指定激励源所在网格的空间位置,把式(16)中的Is用一个时谐源或脉冲源表示,即可把激励源能量同时耦合到天线所在网格当中。经过多个时间步迭代后,电磁波信号将覆盖到整个计算空间,得到整个离散巷道内电磁波信号的能量分布情况。
2 矿井测量试验
分别于2019年4月、2019年9月和2019年12月,在宁煤集团双马煤矿4-1煤辅助运输大巷(以下简称测量巷道),用580 MHz和740 MHz两个频段的无线通信设备,测量天线在巷道内不同位置处的电磁波传播特性,740 MHz的详细测量结果及分析见文献[2]。巷道断面为马蹄形结构,实际最大高度为4.00 m,宽度5.20 m,断面面积16.30 m2,测量范围内不存在分支和弯曲巷道。测量设备射频发射功率30 dBm,1 Mbps时通信速率接收灵敏度为-92 dBm,使用特性阻抗为50 Ω的1 dBi全向垂直极化偶极子天线。测量时收发天线的高度统一为1.70 m,根据等效面积原理[7],可以将测量巷道等效为高3.40 m,宽4.80 m的矩形巷道。实际测量环境和等效巷道如图4和图5所示。

图4 测量环境
Fig.4 Measurement environment
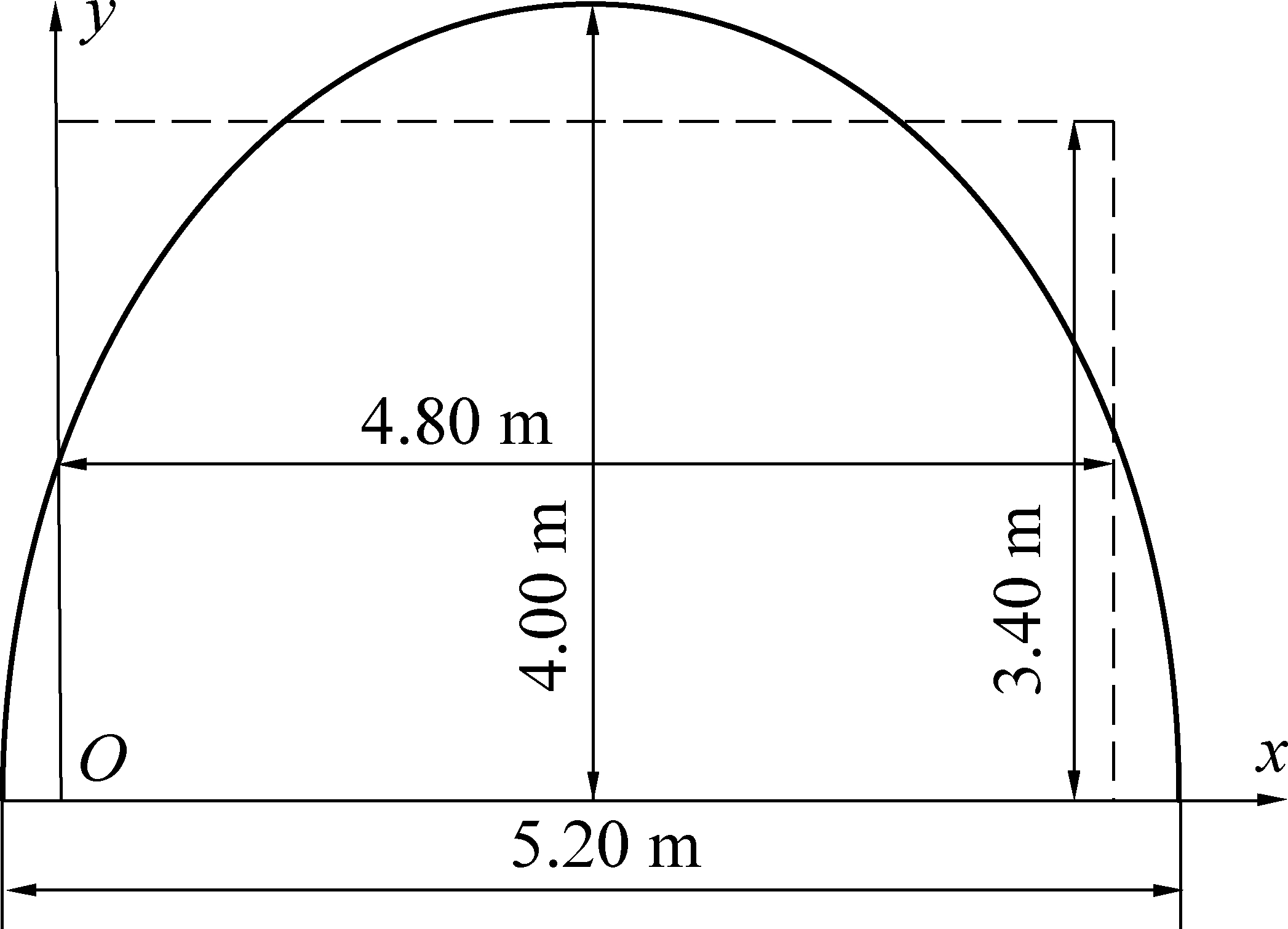
图5 实际巷道及等效矩形巷道断面尺寸
Fig.5 The section size of actual tunnel and equivalent rectangular tunnel
文献[24]研究了矩形巷道载波频率对近场区分阶段的影响。在转折点之前即收发天线相对距离较近时,电磁波信号衰减梯度较大,且信号强度波动幅值大,在转折点之后信号衰减梯度较小。文献[25]根据电磁波信号衰减梯度用临界距离建立巷道传播模型,给出邻近距离与巷道断面较大一个尺寸的平方成正比,与波长成反比,以740 MHz电磁波为参考可估算出在本文测量巷道内收发天线沿巷道z轴向相距56 m附近存在一个电磁波信号衰减梯度的转折点。笔者在该巷道内的多次测量结果表明,收发天线相距小于50 m时,电磁波信号强度波动、衰减幅值和衰减梯度均较大;相距大于50 m时,电磁波信号强度波动趋于平缓,衰减幅值和衰减梯度也逐渐减小。
为减小测量误差,收发天线沿巷道z轴向距离在50 m以内增加采样密度,大于50 m时采样点相对稀疏。沿巷道z轴向各采样点位置分别为1、2、4、8、16、30、50、80、120 m。天线靠近巷帮衰减大,因此,在巷道x水平方向上当收发天线在巷帮附近时也增加采样密度,沿巷道x水平方向上采样点位置分别为0、0.02、0.04、0.10、0.30(巷道宽的1/8)、0.60(巷道宽的1/6)、1.20(巷道宽的1/4)和2.40 m(巷道宽的1/2)。测量时发射天线和接收天线高度均为1.70 m(巷道高的1/2),在各x水平位置上发射天线作为参考点静止不动,接收天线依次移动到各z轴向采样点,等接收信号稳定后,每次采样取20次测量值的平均值作为该点的最终接收信号强度。
3 数值分析
3.1 激励源验证
巷道内无法推导激励源辐射场的解析解,但在自由空间,赫兹偶极子的辐射特性却可以准确计算出来,赫兹偶极子远场的辐射电场解析解[26]为
(17)
式中:j2=-1;I0为初始电流;l为赫兹偶极子长度;k为电磁波波数;θ为仰角;η为介质的波阻抗;r为接收点到赫兹偶极子中心的距离。
740 MHz正弦电磁波载波波长约为0.41 m,对应半波赫兹偶极子天线长度约为0.21 m。单个网格x、y、z方向空间步长分别为0.02、0.02和0.04 m,Rs为50 Ω,仿真天线在y方向占7个网格,其他方向占1个网格,激励源和接收点的水平位置等高。根据1.4节推导的可变内阻电流激励源FDTD迭代方程公式(16),用80×80×7 500个网格作为计算空间,四周再设置10层PML吸收边界防止电磁波反射,模拟电磁波在300 m自由空间内的传播特性。赫兹偶极子天线解析值也使用740 MHz电磁波,天线长0.21 m,仰角为90°等价于FDTD仿真时激励源和接收点具有相同的水平位置。在300 m自由空间内把正弦透明激励源、正弦硬激励源[22]和本文提出的可变内阻激励源耦合到FDTD计算空间,并和文献[26]中的赫兹偶极子解析方程进行对比,计算出740 MHz电磁波在300 m自由空间内的衰减特性如图6所示。可以看出,与正弦透明激励源和硬激励源相比,该可变内阻电流激励源仿真值和半波偶极子天线解析值在自由空间随距离变化的衰减趋势一致,表明该可变内阻激励源,适用于FDTD仿真全向偶极子天线的辐射特性。

图6 激励源仿真值和赫兹偶极子解析值
Fig.6 Simulation values of excitation source and analytical values of Hertz dipole
3.2 巷道模型验证
巷道壁为有耗介质,文献[6]中指出在煤矿巷道内,对于200~4 000 MHz频率范围内的电磁波巷道壁可以作为非磁性低损耗介质,相对介电常数在5~10,巷道壁相对介电常数取8。文献[8]中指出巷道壁电导率影响复介电常数虚部的大小,其对电磁波的影响可以被视为介电常数影响的一部分,根据其试验数据设定巷道壁和PML的电导率为0.01 S/m。从激励源辐射的电磁波经过空气介质传播到巷道壁,一部分电磁波被巷道壁反射,一部分电磁波经过透射进入到巷道壁内部并被四周的PML吸收。最外层采用坐标伸缩PML吸收边界条件[20]。
文献[3]在宽4.00~4.20 m、高3.00~3.50 m的拱形车辆巷道断面中心位置测量了900 MHz电磁波在100 m内的传播特性,根据巷道断面面积等效原理,该巷道可以近似等价为宽4.30 m、高3.40 m的矩形巷道。在宽4.80 m、高3.40 m的等效矩形巷道内测量580 MHz和740 MHz两种电磁波在120 m内的传播特性,2种巷道断面大小较为接近,在此以上述2种巷道的测量值作基准,验证所提仿真模型的准确性。单个网格x、y、z方向空间步长分别为0.02、0.02和0.04 m。仿真各区域的电磁参数见表2。
表2 各区域的电磁参数
Table 2 The electromagnetic parameters of each area
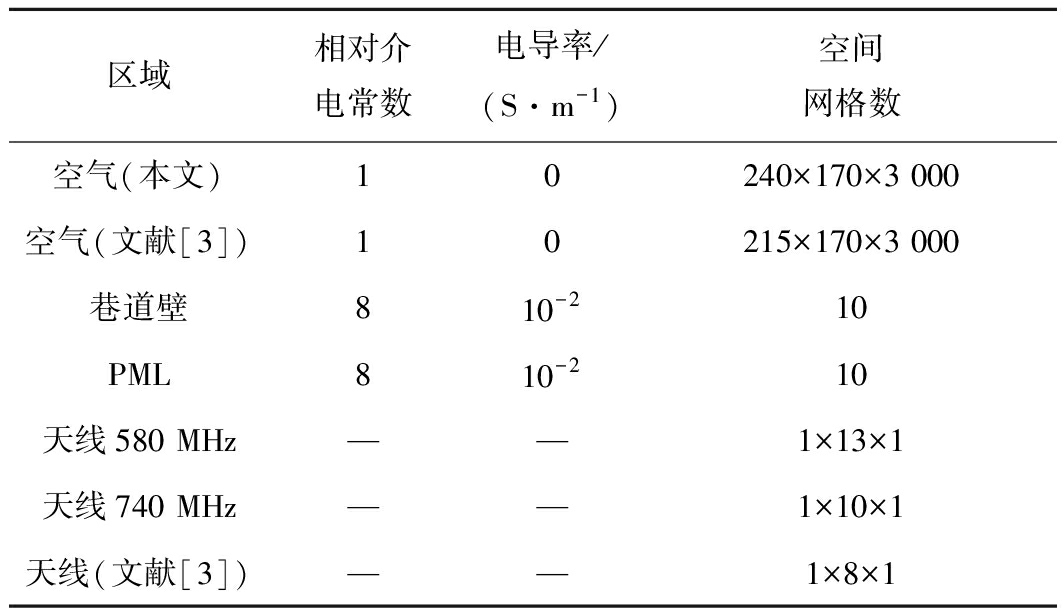
区域相对介电常数电导率/(S·m-1)空间网格数空气(本文)10240×170×3 000空气(文献[3])10215×170×3 000巷道壁810-210PML810-210天线580 MHz——1×13×1天线740 MHz——1×10×1天线(文献[3])——1×8×1
激励源位于巷道断面中心,用正弦波激励出垂直极化波,与测量时使用的垂直极化天线保持一致。在等效矩形巷道内迭代12 500次时间步计算出的580、740、900 MHz电磁波仿真信号强度和3组测量值(本文现场测量值、文献[3])的对比结果如图7所示。

图7 巷道断面中心FDTD仿真值和测量值对比
Fig.7 Comparison of the FDTD calculated value and measured value at the tunnel center
在发射天线附近,3种电磁波信号衰减梯度都比较大,电磁波信号波动周期小;随着发射天线距离的增大,电磁波信号波动周期变大并且衰减强度逐渐减小。3种频率的仿真结果与测量值相比,衰减规律基本一致,表明提出的FDTD矿井电磁波数值计算方法可以分析研究巷道内电磁波传播特性。
3.3 矿井电磁波传播特性
3.3.1 收发天线到巷帮等距
收发天线到同一侧巷帮距离相同的测量场景,与矿井无线通信基站之间和矿井无线通信基站与其他固定无线通信设备之间无线通信实际应用场景一致。仿真巷道宽4.8 m、高3.4 m、长500 m,收发天线的高度同为1.70 m,且均从同一侧巷帮逐渐移动到巷道x水平方向中心,同时到同一侧巷帮距离为0.02、0.04、0.10、0.60(巷道宽的1/8)、1.2(巷道宽的1/4)以及2.4 m(巷道宽的1/2)时,580、740、900 MHz 等3种频率电磁波沿巷道z轴方向的传播特性如图8所示。

图8 收发天线位置对电磁波衰减的影响
Fig.8 Effect of the position of the transceiver antenna on electromagnetic wave attenuation
由图8仿真结果可知无论收发天线到巷帮距离远近,3种电磁波频率在收发天线沿巷道z轴向方向相距50 m左右均存在一个电磁波信号衰减梯度转折点,在转折点之前信号波动强烈、电磁波信号衰减梯度大,转折点之后电磁波信号衰减梯度变小,与测量结果较为一致。
收发天线沿巷道z轴向方向相距500 m且同时距巷帮0.02 m时580、740、900 MHz等3种电磁波信号分别衰减了74、81和83 dB,同时距巷帮2.40 m即位于巷道中心时分别衰减了57、67和70 dB。3种频率电磁波收发天线同时距巷帮0.02 m时比在巷道断面中心时平均多衰减14.6 dB。
收发天线同时从一侧巷帮移动到巷道x水平方向中心位置,在上述各x方向采样点上求出沿巷道z轴向传播的电磁波信号强度的平均值,以便从整体上分析收发天线在x方向上变化时电磁波的衰减规律。收发天线在x水平方向不同位置电磁波沿巷道z轴向方向传播120 m内和500 m内的仿真值和测量值的平均信号强度如图9a和图9b所示。从图9b中可以看出580 MHz和740 MHz 2种电磁波收发天线同时到巷帮不同距离时的仿真值和测量值的变化规律一致。从图9a和图9b中都能看出,收发天线从巷道断面中心到距巷帮0.6 m(巷道宽的1/8)的范围内,3种频率电磁波信号衰减强度较为平缓,靠巷帮越近,衰减强度越大。收发天线沿巷道纵向相距120 m,与位于巷道断面中心相比,收发天线到同一侧巷帮距离为0.02 m时,580、740和900 MHz 等3种电磁波接收信号强度的仿真值分别多衰减了24、26和27 dB。

图9 收发天线沿z方向上的平均信号强度
Fig.9 Average signal strengths of transceiver antenna at z direction of the tunnel
为更清晰地表示收发天线同时距巷帮距离变化时电磁波信号强度的衰减规律,用巷道x水平方向信号衰减梯度来表示,即收发天线在巷道x水平方向从一个位置移动到另一个位置,电磁波信号强度的变化量与x水平方向的距离之比。根据500 m长巷道内的仿真结果,巷道x水平方向各区域的信号衰减梯度见表3。
表3 巷道x水平方向上的信号衰减梯度
Table 3 The signal attenuation gradient of the tunnel in x dircetion
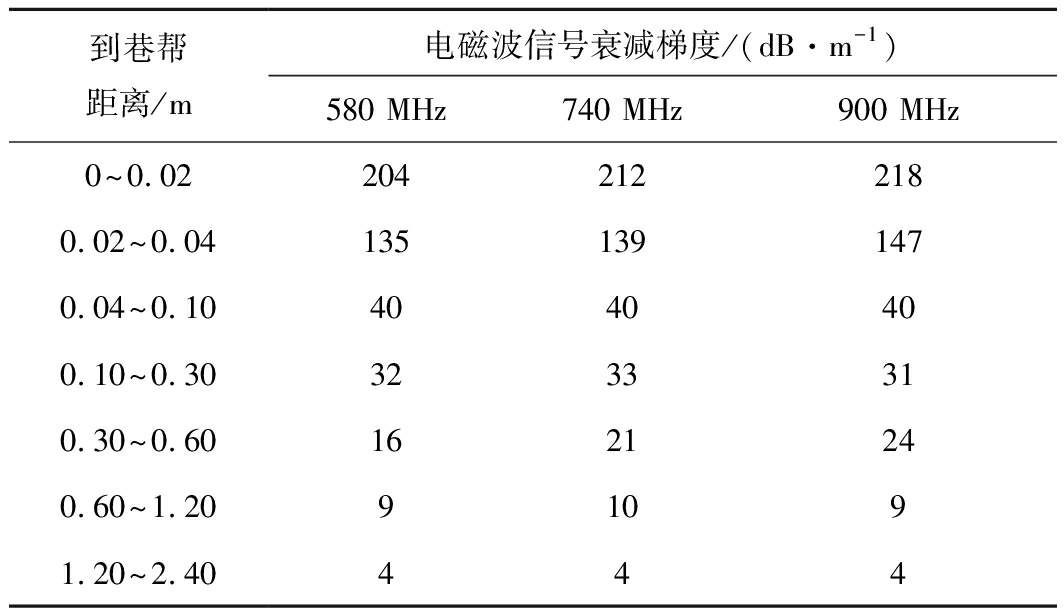
到巷帮距离/m电磁波信号衰减梯度/(dB·m-1)580 MHz740 MHz900 MHz0~0.022042122180.02~0.041351391470.04~0.104040400.10~0.303233310.30~0.601621240.60~1.2091091.20~2.40444
可以得出,收发天线同时距巷帮距离在0.30 ~2.40 m的范围内,3种频率电磁波信号沿巷道x水平方向的电磁波信号平均衰减梯度为11 dB/m;在0.04 ~0.30 m范围内的电磁波信号平均衰减梯度为35 dB/m;在0.02~0.04 m内的电磁波信号平均衰减梯度为140 dB/m;在0~0.02 m范围内为217 dB/m,是0.04~0.30 m范围内的6.2倍,是0.02~0.04 m内的1.6倍。3种频率电磁波在巷道x水平方向上的电磁波信号衰减梯度变化规律基本一致,收发天线同时到巷帮的距离越近,电磁波信号的衰减梯度越大,对巷道内电磁波信号传播特性影响就越大。因此,在不影响行人和行车的条件下,无线通信基站天线应尽量远离巷帮,天线到巷帮的距离最好大于0.02 m,在条件允许的情况下,天线到巷帮的距离宜大于0.04 m,以获得最佳通信效果和通信距离。
3.3.2 收发天线到巷帮不等距
在矿井内另一种常见的应用场景是无线通信基站与无线移动终端之间的无线通信。无线通信基站的天线固定在巷帮附近,无线移动终端在巷道内自由移动,此时收发天线到巷帮的距离不同。因此,需要研究收发天线到巷帮不等距时电磁波在巷道内的传播特性。发射天线到巷帮的距离分别为0、0.02、0.04、0.10、0.30、0.60、1.20、2.40 m,收发天线在巷道z轴向相距500 m时的平均信号强度如图10所示。
580 MHz电磁波收发天线到巷帮不同距离时平均接收信号强度的最大值为-36 dBm,最大值平均位置到发射天线所在巷帮的距离为2.58 m;740 MHz接收信号强度平均最大值为-51 dBm,最大值平均位置到发射天线所在巷帮的距离为2.56 m;900 MH 电磁波信号强度的平均最大值为-57 dBm,最大平均位置到发射天线所在巷帮的距离为2.50 m。
可知,无论发射天线到巷帮的距离有多远以及接收天线与发射天线在同侧或异侧,3种频率电磁波接收信号强度在靠近巷帮附近时较小,接收信号强度的最大值出现在巷道断面中心附近区域。以图10b和图10h中580 MHz电磁波为例,当发射天线距巷帮0.02 m时,信号强度最小值出现在与发射天线同侧的巷帮上,大小为-54 dBm,最大值出现在距发射天线所在巷帮2.6 m处,大小为-46 dBm;当发射天线距巷帮2.40 m时,信号强度最小值也出现在和发射天线同侧的巷帮上,大小为-36 dBm,最大值出现在距发射天线所在巷帮2.40 m处即巷道x水平方向中心位置,大小为-27 dBm。因此,使用无线移动通信终端时最好在巷道断面中心附近,以获得最佳的通信效果。
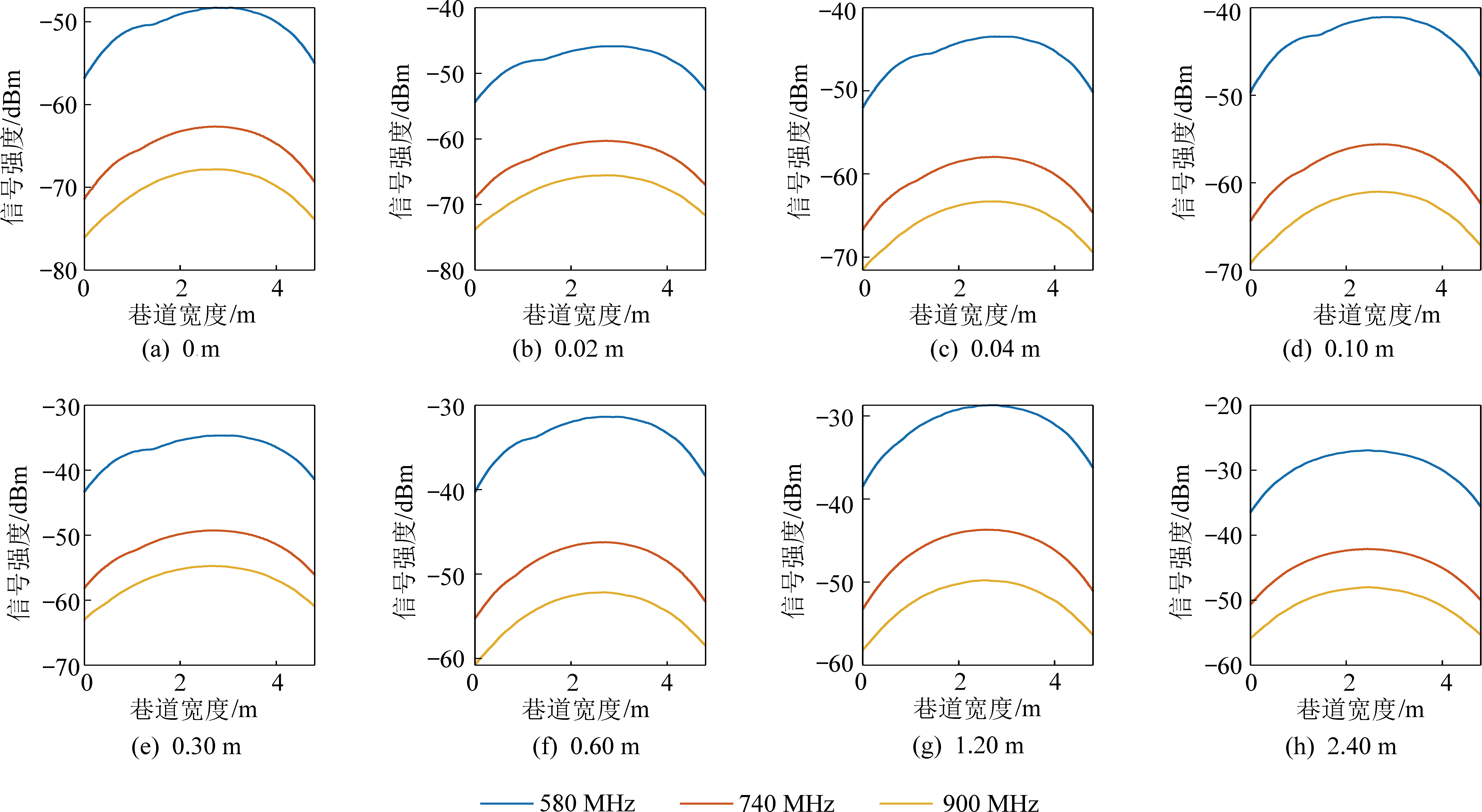
图10 收发天线相距500 m的接收信号强度平均值
Fig.10 The average value of received signal strength within 500 m between receiving and transmitting antennas
4 结 论
1)提出的可变内阻激励源FDTD方法的仿真结果与半波赫兹偶极子天线解析值随距离变化的衰减趋势一致,性能优于正弦透明激励源和硬激励源。
2)在煤矿井下辅运巷道内进行了580 MHz和740 MHz电磁波传输测量试验,并参考其他研究人员的900 MHz矿井电磁波传输测量数据,验证了建立的空气介质+巷道壁+完全匹配层三维巷道模型和可变内阻激励源巷道电磁波传播模型的正确性。
3)收发天线同时到巷帮距离在0.30~2.40、0.04~0.30、0.02~0.04和0~0.02 m范围内580、740和900 MHz电磁波信号沿巷道x水平方向的电磁波信号平均衰减梯度分别为11、35、140和217 dB/m。因此,为获得最佳通信效果和通信距离,无线通信基站天线到巷帮的距离最好大于0.02 m,在条件允许的情况下宜大于0.04 m。
4)收发天线沿巷道z轴向相距500 m时,580、740和900 MHz电磁波,发射天线到巷帮的距离为0~2.4 m内平均接收信号强度的最大值分别为-36、-51和-57 dBm,每种电磁波最大值平均位置到发射天线所在巷帮的距离分别为2.58、2.56和2.50 m。基站天线到巷帮距离已定的条件下,无线移动终端在巷道断面中心附近区域,可以获得最大接收信号强度,取得最佳通信效果。
[1] 孙继平. 煤矿安全生产监控与通信技术 [J]. 煤炭学报, 2010, 35(11): 1925-1929.
SUN Jiping. Technologies of monitoring and communication in the coal mine [J]. Journal of China Coal Society, 2010, 35(11): 1925-1929.
[2] 孙继平, 张高敏. 矿用5G频段选择及天线优化设置研究 [J]. 工矿自动化, 2020, 46(5): 1-7.
SUN Jiping, ZHANG Gaomin. Reaearch on 5G frequency band selection and antenna optimization setting in coal mine[J]. Industry and Mine Automation,2020,46(5): 1-7.
[3] 张跃平, 张文梅, 盛剑桓, 等. 900 MHz无线电波在地下长壁煤矿的传播 [J]. 煤炭学报, 2002, 27(1): 83-87.
ZHANG Yueping, ZHANG Wenmei,SHENG Jianhuan, et al. Radio propagation at 900 MHz in underground coal mines[J]. Journal of China Coal Society,2002,27(1): 83-87.
[4] RANJAN A, SAHU H, MISRA P. Modeling and measurements for wireless communication networks in underground mine environments [J]. Measurement, 2020, 149(1): 1-12.
[5] BRISO-RODRIGUEZ C, FRATILESCU P, XU Y. Path loss modeling for train-to-train communications in subway tunnels at 900/2400 MHz [J]. IEEE Antennas and Wireless Propagation Letters, 2019, 18(6): 1164-1168.
[6] EMSLIE A G, LAGACE R L, STRONG P F. Theory of the propagation of UHF radio waves in coal mine tunnels [J]. IEEE Transactions on Antennas and Propagation, 1975, 23(2): 192-205.
[7] GUAN K, ZHONG Z, AI B, et al. Modeling of the division point of different propagation mechanisms in the near-region within arched tunnels [J]. Wireless Personal Communications, 2013, 68(3): 489-505.
[8] ZHOU C, WAYNERT J, PLASS T, et al. Attenuation constants of radio waves in lossy-walled rectangular waveguides [J]. Progress in Electromagnetics Research, 2013, 142: 75-105.
[9] MAHMOUD S F, WAIT J R. Geometrical optical approach for electromagnetic wave propagation in rectangular mine tunnels [J]. Radio Science, 1974, 9(12): 1147-1158.
[10] 孙继平,张高敏. 基于混合射线追踪的矿井电磁波分析方法研究 [J]. 煤炭学报, 2022, 47(7): 2834-2843.
SUN Jiping, ZHANG Gaomin. Research on mine electromagnetic wave analysis method based on mixed ray tracing[J]. Journal of China Coal Society, 2022,47(7):2834-2843.
[11] ZHOU Chenming. Ray tracing and modal methods for modeling radio propagation in tunnels with rough walls [J]. IEEE Trans Antennas Propag,2017,65(5):2624-2634.
[12] FOROOSHANI A E, BASHIR S, MICHELSON D G, et al. A Survey of Wireless Communications and Propagation Modeling in Underground Mines [J]. IEEE Communications Surveys & Tutorials,2013,15(4):1524-1545.
[13] 张 帆. 矿井移动通信理论与技术 [M]. 哈尔滨: 哈尔滨工业大学出版社, 2021:28-31.
[14] TAGUCHI K, IMAI S, KASHIWA T, et al. FDTD analysis of radio wave propagation at intersection surrounded by concrete block walls in residential area for inter-vehicle communications using 720 MHz band [J]. IEICE Transactions on Electronics, 2012, E95(1):79-85.
[15] JIANG Z H, LIU S C, MALEKIAN R. Analysis of a whole-space transient electromagnetic field in 2.5-dimensional FDTD geoelectric modeling [J]. IEEE Access, 2017, 5: 18707-18714.
[16] AHDAB Z E, AKLEMAN F. An efficient 3-D FDTD-PE hybrid model for radio wave propagation with near-source obstacles [J]. IEEE Transactions on Antennas and Propagation, 2019, 67(1): 346-355.
[17] 张双狮, 雷朝军, 刘迎辉, 等. 瞬态电磁场三维时域有限差分模拟研究 [J]. 电子科技大学学报, 2019, 48(1): 13-21.
ZHANG Shuangshi, LEI Chaojun, LIU Yinghui, et al. On simulation of 3D-FDTD for transient electromagnetic field [J]. Journal of University of Electronic Science and Technology of China, 2019, 48(1): 13-21.
[18] KWEON J H, PARK M S, CHO J, et al. FDTD analysis of electromagnetic wave propagation in an inhomogeneous ionosphere under arbitrary-direction geomagnetic field [J]. Journal of Electromagnetic Engineering and Science, 2018, 18(3): 212-214.
[19] YEE K S. Numerical solution of initial boundary value problems involving maxwell’s equations in isotropic media [J]. IEEE Transactions on Antennas & Propagation, 1966, 14(5): 302-307.
[20] WENG C C, WEEDON W H. A 3D perfectly matched medium from modified maxwell’s equations with stretched coordinates [J]. Microwave and Optical Technology Letters, 1994, 7(13): 599-604.
[21] BEKMAMBETOVA F, TRIVERIO P. A dissipation theory for potentials-based FDTD for lossless inhomogeneous media [J]. IEEE Antennas and Wireless Propagation Letters 2021, 21(3): 486-490.
[22] COSTEN F, BERENGER J P, BROWN A K. Comparison of FDTD hard source with FDTD soft source and accuracy assessment in debye media [J]. IEEE Transactions on Antennas & Propagation, 2009, 57(7): 2014-2022.
[23] DEMIR V. Formulations for modeling voltage sources with RLC impedances in the FDTD method [J]. Applied Computational Electromagnetics Society Journal, 2016, 31(9): 1020-1027.
[24] 焦晓龙, 成凌飞, 张薇静, 等. 矩形巷道载波频率对近场区分界点的影响 [J]. 煤炭科学技术, 2021, 49(9): 124-128.
JIAO Xiaolong,CHENG Lingfei,ZHANG Weijing,et al.Influence of carrier frequency on demarcation points of near field in rectangular roadway[J]. Coal Science and Technology,2021,49(9):124-128.
[25] KLEMENSCHITS T, BONEK E. Radio coverage of road tunnels at 900 and 1800 MHz by discrete antennas [C]// 5th IEEE International Symposium on Personal. Hague: IEEE,1994:411-415.
[26] GURU B S, HIZIROGLU H R. Electromagnetic field theory fundamentals [M]. Cambridge:Cambridge University Press, 2004.
