
移动扫码阅读

移动扫码阅读
Study on vibration propagation law of frozen clay blasting in deep mine shaft
借鉴立井冻结基岩爆破的成功经验,深部立井冻结黏土爆破施工在矿井建设中逐步使用。 冻结黏土爆破主要面临2 个问题:①冻结黏土的密实坚硬程度不如岩石,导致土体爆破效率低。 ②冻土爆破装药量要合理的控制,防止造成冻结管和立井井壁的损伤。 关于冻土爆破的研究,早期主要研究青藏高寒区的冻土爆破,张俊兵等[1]依托青藏高原多年冻土区进行了冻土爆破漏斗试验,确定了高含冰量冻土的爆破参数。 随着人工冻结法的应用,宗琦等[2]最早提出一种宽孔距崩落技术,该技术主要控制炮眼密集系数来提高爆破掘进效率。 文献[3-4]根据理论研究与现场试验,总结了多年冻土和季节冻土的爆破方法。 李志敏等[5]探究了冻结砂土的爆破机理,将爆破作用区域划分为空腔、挤压区、破碎区、裂纹区和弹性振动区,细化了冻结砂土爆破破坏形式。 李涛等[6]利用TDW-200 冻土三轴试验机对饱和冻结灰砂岩进行了试验,获得了不同围岩条件下冻结灰砂岩弹性模量的演化规律。 张慧梅等[7]研究了冻融循环下岩石的物理力学性质,研究发现:随着冻融循环次数增多和围压增加,岩石破坏形式逐渐由脆性转化为延性。 李栋伟等[8]通过构建人工冻土BP 神经网络本构模型,较好地模拟了冻土中复杂应力路径变形特征。 但对冻土中爆破应力波的振动传播规律及能量特征,没有更深一步地进行研究。 因此开展冻结黏土爆破振动监测,研究冻结黏土中爆破应力波的传播规律和爆破能量分布,进行爆破方案的合理优化,对于立井冻结爆破施工具有重要意义。 随着小波(包)分析在工程中的应用,林大超等[9]研究发现小波分析不仅能给出爆破振动能量在不同频率范围内的相对分布规律,还可以给出不同频率带上振动分量的分布和实际衰减规律,在工程中的应用越发广泛。 针对不同的工程进行小波(包)能量分析,发现不同的爆破介质能量的衰减规律是不同的。 例如在露天采矿场边坡[10]、地 下 工 程 爆 破[11-12]、采 石 场[13] 等 进 行 小波(包)分析,得出的能量衰减规律呈现出差异性。而目前对冻结黏土单一介质的爆破能量分析还鲜见研究,大多是针对砂土、岩石等类型的研究。 其中仅有单仁亮[14]等结合立井模型试验,对冻结岩壁的能量衰减进行了预测,与冻结黏土爆破较为接近。
针对立井冻土单一介质爆破振动传播规律的研究较少,尤其是应力波在冻结黏土中的传播。 以赵固二矿西风井冻结爆破掘进为背景,在深690 m 处开展冻结黏土爆破试验,分析爆破振动在冻土中的传播规律,并结合小波(包)分析得到振动时能量分布特征,以期指导深井冻结黏土爆破的工程实践,保证周围冻结管和已浇筑井壁的安全。
根据爆破漏斗理论,在立井冻结黏土段设计单孔爆破漏斗试验。 该土层冻结温度-15 ℃,极限强度为8.16 MPa,黏聚力16.6~214.1 kPa。
试验炮孔孔径设计为50 mm,采用水胶炸药,药卷长度320 mm,每孔半卷炸药。 相邻炮孔设计间距不小于1.8 m,炮孔深度按0.05 m 逐渐增大,最浅炮孔深度为0.35 m,最深炮孔深度为0.50 m,共布置了4 个炮孔(Ⅰ、Ⅱ、Ⅲ、Ⅳ)、5 台振动传感器。 炮孔编号1~4,传感仪依次为A、B、C、D、E 具体布置如图1所示。
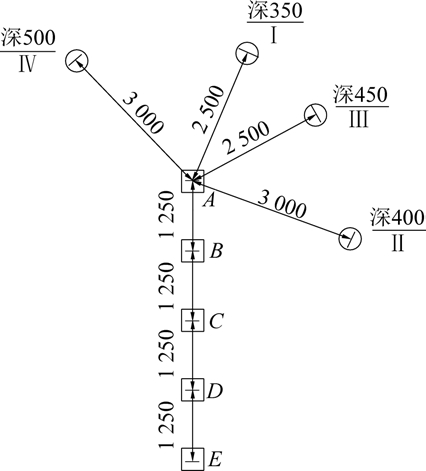
图1 炮孔及传感仪布置示意
Fig.1 Schematic of holes and sensor arrangement
根据炸药的爆破作用理论和大量的现场爆破表明,炸药爆破产生冲击波和地震波,二者引起的振动,是对周围岩土体产生破坏作用的重要因素。 而振动速度的大小与其破坏程度是成正相关的,常把爆破振动速度作为当前国内外爆破振动效应和爆破安全控制监测的标准。
结合目前国内爆破振动标准,本次试验将垂直、水平径向和水平切向3 个速度分量作为试验参量。
测试前,将爆破振动传感器安装在选定的测点位置,第1 个测点布置在距离爆破孔2.5 m 的位置,共布置了5 台测振仪,每个测点相距125 cm,最后一个测点距离井壁内缘1.8 m,仪器测点与爆点径直方向为x,切向方向为y,垂直方向为z,现场布置如图2 所示。

图2 传感器的布置
Fig.2 Arrangement of measuring sensors
冻结黏土的松动爆破效果如图3 所示。

图3 爆破效果
Fig.3 Blasting effect
4 个炮孔中,Ⅰ号炮孔爆破引起的振动速度最大,且振动具有规律性;Ⅱ号和Ⅳ号炮孔振动速度小,且振动速度无规律;Ⅲ号炮孔的垂直速度曲线跳跃较大,无规律性。 因此,把Ⅰ号炮孔作为典型爆源,对各测点的监测结果进行分析,其中测距R 利用余弦公式计算得出,三向振动速度取振动时程中的最大值,监测结果见表1。
表1 监测数据
Table 1 Monitoring data

测距/m 振动速度/(cm·s-1)径向 切向 垂向 矢量和3.000 6.67 5.52 14.18 14.79 3.983 4.45 10.36 14.72 14.97 5.085 3.43 0.63 5.26 5.28 6.243 4.38 2.76 4.13 6.17 7.430 1.62 5.21 2.51 5.24
从表1 中看,各向振动速度呈现出差异,垂向方向振动速度>径向方向振动速度>切向方向振动速度,说明了冻土爆破后应力波的传播主要是沿某个特定方向。 单仁亮[15]在对冻结岩壁的振速研究中,也得出岩体振动具有明显方向差异性,说明了冻土和岩石爆破的振速传播均具有方向的差异性。 对于爆破振动速度v,我国普遍使用萨道夫斯基经验公式[16]:
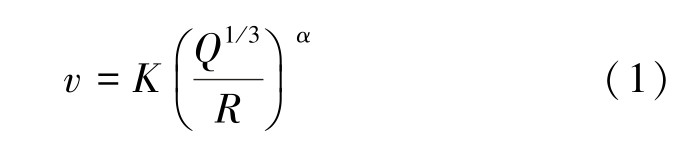
式中:K 为场地系数;α 为衰减系数;Q 为单段最大装药量,kg;R 为测点与爆破位置距离,m。
炸药量为0.15 kg,则:![]() 那么萨道夫斯基公式为:v =K(0.53/R)α 。 将数据载入到Origin,利用Origin 中的自定义拟合函数进行拟合,可以得到K 和α,见表2,拟合的曲线如图4所示。
那么萨道夫斯基公式为:v =K(0.53/R)α 。 将数据载入到Origin,利用Origin 中的自定义拟合函数进行拟合,可以得到K 和α,见表2,拟合的曲线如图4所示。
表2 K 和α 拟合结果
Table 2 Fitting results of K and α
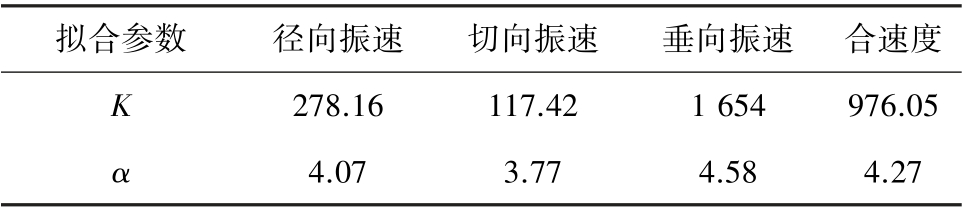
拟合参数 径向振速 切向振速 垂向振速 合速度K 278.16 117.42 1 654 976.05 α 4.07 3.77 4.58 4.27
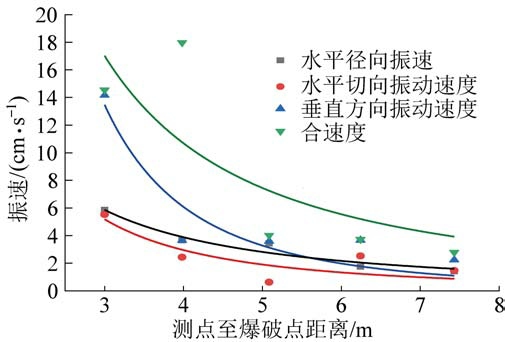
图4 各分量及合速度拟合曲线
Fig.4 Fitting curves of each component and resultant velocity
曲线拟合程度:径向方向、切向方向、垂向方向以及合速度方向的决定系数R2 分别为0.97、0.97、0.98 和0.98,相关性较好,其中径方向相关性最好。 将拟合得到的K、α 值代入萨道夫斯基公式,得到各分量及合速度的拟合公式如下:
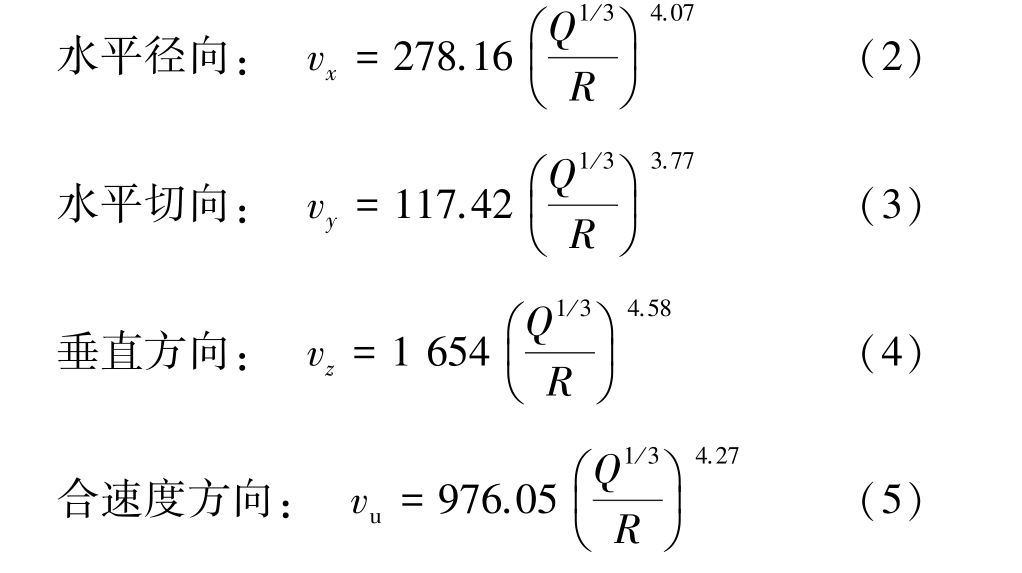
式中:vx 为水平径向的振动速度,cm/s;vy 为水平切向的振动速度,cm/s;vz 为垂直方向的振动速度,cm/s;vu 为合速度,cm/s。
由于传感仪距离爆破点较近,且传感仪是插入土体中的,爆破后垂直方向上受到的冲击大,振动信号的采集出现了失真,导致拟合后的K、α 过大。 但其他2 个方向上的拟合较为正常,可为冻土爆破振动传播的衰减规律提供一定的借鉴。 《爆破安全规程》中对爆破频率超过50 Hz 的巷道振动速度规定不能超过30 cm/s,将30 cm/s 作为振动速度控制值代入拟合公式,在一定药量下可以计算出安全距离R,根据R 的取值,合理布置冻结管和立井井壁的浇筑位置。
小波(包)分析是基于小波分析发展而来的,它能根据信号特性和分析要求自适应的选择相应频带与信号频谱相匹配,是比小波分解更为精细的一种分解方法[9]。 爆破振动信号进行小波(包)分解时,最优分解层数的确定依据信号分析的特征和振动记录仪的最小工作频率来确定[17]。 监测采用仪器为TC4850 爆破测振仪,其最小工作频率为5 Hz,由于爆破振动信号的频率一般集中在200 Hz 范围以内,根据采样定律[18],设置信号的采样频率为16 kHz,其奈奎斯特频率为8 kHz。 根据小波(包)分析的原理将信号分解到8 层,共有28个小波(包),则其对应于的最低频段为0~31.25 Hz。
小波基的选择在爆破振动信号分析中是至关重要的,不同的小波基会导致分析结果千差万别。Daubechies 小波系列具有良好的紧支撑性、光滑性以及对称性[19]。 根据算法进行matlab 编程,用db5~db10 的小波基对A 测点的振动信号进行8 层小波(包)分解与重构,得出重构误差见表3。
表3 小波重构误差
Table 3 Reconstruction errors of wavelet packet analysis
注:N 为小波的序号,N 取2,3,…,10。
dbN db5 db6 db7 db8 db9 db10误差/(10-18) 7.35 4.63 9.07 22.5-118.8-58.6
从表3 可以看出,db6 小波基对应的重构误差较小,因此选用db6 对振动信号进行小波(包)分解。
依据小波分析原理将振动信号分解至第8 层,设S8,j所对应的能量为E′8,j,则有:
式中:xj,k(j =0,1,2,…,2i-1;k =1,2,…,m) 为重构信号S8,j的离散幅值。 S8,j(t)为8 层第j 个频带上的重构信号;k 为离散点的个数;t 为时间变量。
设被分析振动信号的总能量为E′,则有:
各频带能量的百分比为:
其中:j=0,1,2,…,28-1。
通过计算爆破振动信号经小波分解后信号总能量和不同频带能量所占百分比,分析冻结黏土爆破振动信号在传播过程中的能量分布。 并通过小波(包)的分解,获得不同频带的能量及百分比。
3.4.1 冻结黏土爆破振动能量的衰减
根据试验得到的振动信号总能量,作出不同测点处的振动能量分布如图5 所示,从图5 中可以看出爆破作用下各点振动能量随测点距离的变化。
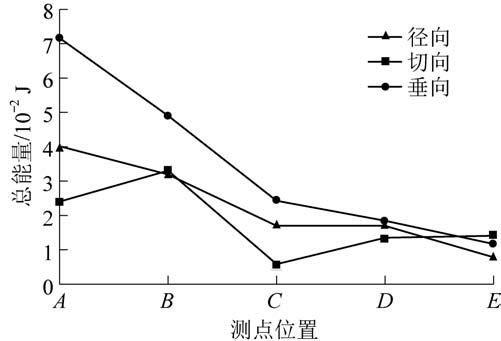
图5 爆破总能量随测点变化的曲线
Fig.5 Total energy of blasting vibration signal changing with measuring point
由图5 可得,立井冻结黏土爆破振动信号与测点环境、爆破距离有关。 由于测点距离爆点仅3.0 ~7.43 m,炸药爆破后能量首先沿冻土传递到A 测点,然后随着距离的增加,能量在冻土中逐渐耗散,传递到测点E 时,能量已经大幅降低。 总体曲线呈现出由A 测点向E 测点逐渐衰减的过程。 此外,从图5 中3个方向上的总能量变化曲线中可以看出,距离爆点0~6.243 m 以内,3 个分量上的总能量呈现出E′z>E′x >E′y 的规律,从另一个方面说明了立井冻结黏土爆破能量的传播是从内到外的径向传播。
3.4.2 不同频率的能量占比
为分析不同方向上的冻结黏土能量占比分布,了解冻结黏土能量的扩散规律,下面以A 测点为例,选取0~500 Hz 频率内的能量,具体分析冻结黏土爆破3 个方向上的能量占比分布规律(图6)。
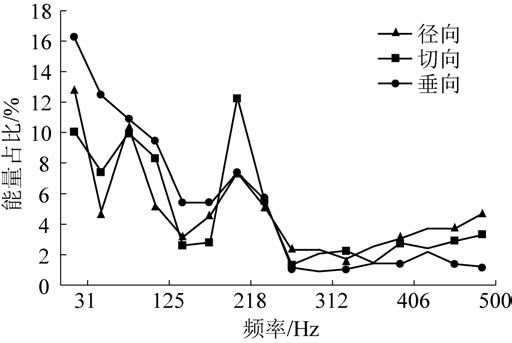
图6 测点A 的能量衰减趋势
Fig.6 Energy decay trend at point A
根据图6 可以看出,能量处于0 ~187 Hz 时,能量占比急剧下降,当能量在218 Hz 左右时,其占比又有所回升。 在218~250 Hz,冻土爆破振动能量发生了剧烈衰减,之后一直保持平稳的衰减状态。 可以得出:此次爆破振动信号能量的变化是在高频段衰减快,但是波动很大,低频段衰减慢,但是稳定。在高频段,能量先急剧下降,然后会频繁波动,会有所回升,达到峰值,之后能量一直衰减。 从能量占比来看,冻结黏土爆破振动能量主要集中在0 ~250 Hz。 在低频段切向分量能量占比较大,而在高频段径向分量能量占比较大。 张广辉等[20]对循环加载下冲击倾向性煤能量耗散进行了研究,从能量的角度发现:耗散能同样呈现先迅速降低,后缓慢增长的趋势。 依据式(8)将测点的能量占比进行求解,做出各点在不同频率的能量占比如图7 所示。

图7 各测点能量分布
Fig.7 Energy distribution of each measuring point
从图7 中可以得出,径向和切向的两个分量的能量占比主要集中在250 Hz 以内。 而各个测点的能量占比趋势也是符合先逐渐减小,然后在125 Hz左右增加,在218 Hz 处达到顶点,然后呈波动逐渐衰减,向低频段移动。 虽然个别测点存在能量波动较大的现象,与爆破现场不稳定有关。 值得关注的是轴向的能量变化趋势较于径向和切向更为明显,变化更大。 即下降比径向和切向更快,突增也比径向和切向更为明显,在高频段的频率占比也较大,易引起共振现象。
3.4.3 爆破振动能量的回归分析
爆破振动能量的衰减过程极其复杂,李洪涛等[21]将单段、多段爆破最大药量与总药量视为定值,推导出爆破振动能量衰减公式,该公式在应用研究中,取得了积极的成果。 但由于药量定值的限制,还存在一定误差。 单仁亮等[14]利用量纲分析法推导出的公式,较好弥补了这个缺点。 参考单仁亮等[14]研究,将岩石爆破振动参数转换为冻结黏土爆破参数进行研究。 该公式将能量E′与等效药量Q1、弹性模量E 、密度ρ 联系起来,函数关系如下:
式中:K1为与冻结黏土的密度、弹性模量有关的参数;φ 为相关系数。
结合萨道夫斯基公式,将爆破振动能量衰减公式简化为:
根据式(8)编写拟合函数,利用Origin 软件求解的总能量值,进行数据的拟合。 以径向为例,如图8 所示,拟合回归系数见表4。
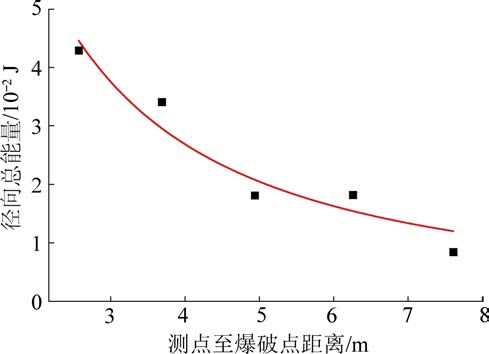
图8 冻土爆破能量衰减回归曲线
Fig.8 Regression of blasting energy attenuation in frozen soil
表4 中径向、垂直方向上的拟合决定系数达到0.8 以上,切向的相关性较差,冻结黏土爆破引起冻土各方向上的能量随距离的增加呈衰减趋势。 垂向的K 值较大,是因为垂向为炮孔自由面方向,爆破近区能量做功大,引起的振动也较大,由于能量快速释放,爆破远区急剧下降。
表4 能量衰减拟合系数
Table 4 Fitting coefficient of energy attenuation
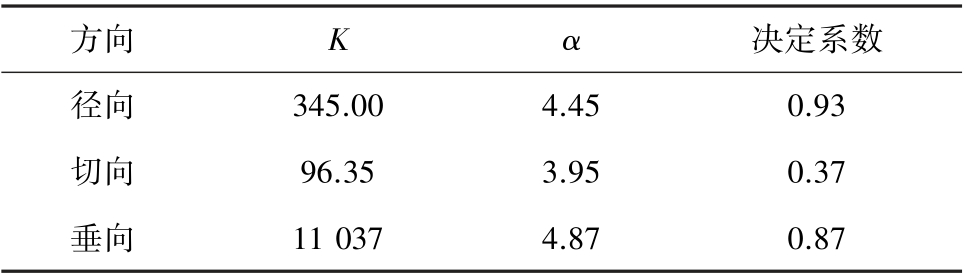
方向 K α 决定系数径向 345.00 4.45 0.93切向 96.35 3.95 0.37垂向 11 037 4.87 0.87
1)冻结黏土爆破各向振动速度存在一定差异,垂向振动速度>径向振动速度>切向振动速度,冻土爆破后应力波的传播主要是沿某个特定方向。
2)运用萨道夫斯基公式对单一冻结黏土介质爆破振动速度进行了拟合,获得了冻结黏土爆破的萨氏拟合公式。
3)深井冻结黏土爆破时,振动信号能量在高频段波动较大但衰减快,低频段相对平稳且衰减缓慢。在高频段,能量首先急剧下降,然后出现频繁波动,达到峰值后一直衰减。 垂向的能量变化趋势较于径向和切向更为明显,变化更大,下降速率径向和切向更快,突增也比径向和切向更为明显。
4)运用量纲分析法对冻结黏土爆破能量信号进行回归分析,得出了冻结黏土爆破各方向上的能量衰减规律。
[1] 张俊兵,潘卫东,傅洪贤.青藏铁路多年高含冰量冻土爆破漏斗的试验研究[J].岩石力学与工程学报,2005,24(6):1077-1081.ZHANG Junbing,PAN Weidong,FU Hongxian.Experimental study on the explosion crater of ice-rich frozen soil along Qinghai-Tibet railway[J].Chinese Journal of Rock Mechanics and Engineering,2005,24(6):1077-1081.
[2] 宗 琦,傅菊根,徐华生.立井冻土掘进爆破技术的研究与应用[J].岩土力学,2007,28(9):1992-1996.ZONG Qi,FU Jugeng,XU Huasheng.Study and application of frozen soil blasting technique in shaft [ J]. Rock and Soil Mechanics,2007,28(9):1992-1996.
[3] 马芹永.多年冻土和人工冻土的爆破试验与方法研究[J].土木工程学报,2004,37(9):75-78.MA Qinyong.A study on blasting tests and methods for permafrost and artificially frozen soils[J].China Civil Engineering Journal,2004,37(9):75-78.
[4] 谭忠盛,况成明,杨小林,等.风火山多年冻土隧道施工爆破技术研究[J].岩石力学与工程学报,2006,25(5):1056-1061.TAN Zhongsheng,KUANG Chengming,YANG Xiaolin,et al.Re⁃search on blasting technology for construction of Fenghuoshan Tun⁃nel in permafrost[J].Chinese Journal of Rock Mechanics and En⁃gineering,2006,25(5):1056-1061.
[5] 李志敏,汪旭光,汪 泉,等.冻结砂土爆破作用区域内损伤模型分析[J].工程爆破,2018,24(3):4-9,34.LI Zhimin,WANG Xuguang,WANG Quan,et al.Analysis of the damage model of frozen sandy soil in blasting area[J].Engineering Blasting,2018,24(3):4-9,34.
[6] 李 涛,马永君,刘 波,等.循环荷载作用下冻结灰砂岩强度特征与弹性模量演化规律[J].煤炭学报,2018,43(9):2438-2443.LI Tao,MA Yongjun,LIU Bo,et al.Strength characteristics and e⁃lastic modulus evolution of frozen gray sandstone under cyclic load⁃ing[J].Journal of China Coal Society,2018,43(9):2438-2443.
[7] 张慧梅,夏浩峻,杨更社,等.冻融循环和围压对岩石物理力学性质影响的试验研究[J].煤炭学报,2018,43(2):441-448.ZHANG Huimei,XIA Haojun,YANG Gengshe,et al.Experimental research of influences of freeze-thaw cycles and confining pressure on physical-mechanical characteristics of rocks[J].Journal of China Coal Society,2018,43(2):441-448.
[8] 李栋伟,陈军浩,周 艳.复杂应力路径人工冻土三轴剪切试验及本构模型[J].煤炭学报,2016,41(S2):407-411.LI Dongwei,CHEN Junhao,ZHOU Yan.Elastic-plastic constitutive model of artificial frozen soil based on cascade-correlation artificial neural network[J].Journal of China Coal Society,2016,41(S2):407-411.
[9] 林大超,施惠基,白春华,等.基于小波变换的爆破振动时频特征分析[J].岩石力学与工程学报,2004,23(1):101-106.LIN Dachao,SHI Huiji,BAI Chunhua,et al. Time-frequency charac-teristic analysis of blasting vibration based on wavelet transform [ J ]. Chinese Journal of Rock Mechanics and Engineering,2004,23(1):101-106.
[10] 宁瑞峰,张世平.小波(包)分析在爆破震动信号能量衰减规律中的应用[J].爆破,2014,31(1):1-4,37.NING Ruifeng,ZHANG Shiping.Application of wavelet packet a⁃nalysis in vibration signal energy attenuation blasting law[J].Blasting,2014,31(1):1-4,37.
[11] 蒋复量,周科平,邓红卫,等.基于小波理论的井下深孔爆破振动信号辨识与能量衰减规律分析[J].煤炭学报,2011,36(S2):396-400.JIANG Fuliang,ZHOU Keping,DENG Hongwei,et al.Theun der⁃ground mines deep-hole blasting vibration signals identification and energy attenuation law s analysis based on wavelet theory[J].Journal of China Coal Society,2011,36(S2):396-400.
[12] 凌同华,李夕兵.地下工程爆破振动信号能量分布特征的小波(包)分析[J].爆炸与冲击,2004,24(1):63-68.LING Tonghua,LI Xibing.The features of energy distribution for blast vibration signals in underground engineering by wavelet packet anal-ysis[J].Explosion and Shock Waves,2004,24(1):63-68.
[13] 晏俊伟,龙 源,方 向,等.基于小波(包)变换的爆破地震波时频特征提取及分析[J].振动与冲击,2007,26(4):25-29,167.YAN Junwei,LONG Yuan,FANG Xiang,et al.Time-frequency characteristics extracting and analysis of blasting seismic wave based on wavelet packet transformation[J].Journal of Vibration and Shock,2007,26(4):25-29.
[14] 单仁亮,白 瑶,宋永威,等.冻结立井模型爆破振动信号的小波(包)分析[J].煤炭学报,2016,41(8):1923-1932.SHAN Renliang,BAI Yao,SONG Yongwei,et al.Wavelet packer analusis of blasting signals of freezing blasting shaft model[J].Journal of China Coal Society,2016,41(8):1923-1932.
[15] 单仁亮,宋立伟,白瑶,等.爆破作用下冻结岩壁损伤评价的模型试验研究[J].岩石力学与工程学报,2014,33(10):1945-1952.SHAN Renliang,SONG Liwei,BAI Yao,et al.Model test studies of damage evaluation of frozen rock wall under blasting loads[J].Chinese Journal of Rock Mechanics and Engineering, 2014,33(10):1945-1952.
[16] 中华人民共和国国家标准编写组.GB6722—2014 爆破安全规程[S].北京:中国标准出版社,2014.
[17] 段军彪.基于损伤累积的爆破振动波能量传播与衰减规律研究[D].焦作:河南理工大学,2018.DUAN Junbiao.Propagation and attenuation of blasting vibration wave energy based on damage accumulation[D].Jiaozuo:Henan Polytechnic University,2018.
[18] 李朝阳,宋玉普,车 轶.混凝土的单轴抗压疲劳损伤累积性能研究[J].土木工程学报,2002,35(2):38-40.LI Chaoyang,SONG Yupu,CHE Yi.Study on cumulative damage behavior of concrete under uniaxial cyclic load[J].China Civil Engineering Journal,2002,35(2):38-40.
[19] I Daubechies.Orthonormal bases of compactly supported wavelets[J].Commun Pure and Appl Math,1988,41(7):909-996.
[20] 张广辉,欧阳振华,邓志刚,等.循环加载下冲击倾向性煤能量耗散与损伤演化研究[J].煤炭科学技术,2017,45(2):59-64.ZHANG Guanghui,OUYANG Zhenhua,DENG Zhigang,et al.Study on energy dissipation and damage evolution of bump prone⁃ness coal under multi cyclic loadings[J].Coal Science and Tech⁃nology,2017,45(2):59-64.
[21] 李洪涛,卢文波,舒大强,等.爆破地震波的能量衰减规律研究[J].岩石力学与工程学报,2010,29(S1):3364-3369.LI Hongtao,LU Wenbo,SHU Daqiang,et al.Study of energy at⁃tenuation law of blastinduced seismic wave[J]. Chinese Journal of Rock Mechanics and Engineering,2010,29(S1):3364-3369.