
移动扫码阅读

移动扫码阅读
Study on positioning strategy and technology at end of shearer based on ultra-wideband system
自实现机械化采矿后,进一步实现智能化以解放矿工成为世界采矿界共同追求的前沿技术[1-2]。采煤机是综采工作面的核心设备,要实现智能化开采必须实现采煤机智能化,监测采煤机在工作面的位置是实现智能化、无人化开采的关键。 基于惯性导航系统的采煤机定位技术作为实现综采工作面自动化的一项关键技术,但是纯惯性导航定位系统随着时间增加存在严重的漂移现象。 REID 等[3]利用零速校正技术对惯性导航系统的漂移误差进行抑制。 李昂等[4]提出了惯性导航与轴编码器组合的采煤机定位技术,结合航位推算算法获得采煤机的位置坐标,该方法能够减小惯性导航的误差累积。张博渊等[5]提出了基于两点法的惯性导航元件安装偏差与初始对准偏差校准算法,分析惯性导航系统确定性偏差对定位精度的影响,并提出了补偿方法。 鲁程等[6]提出了一种多套惯导系统之间冗余的定位算法, 利用扩展卡尔曼滤波对载体的位置进行估计。 但是惯性导航系统在长时间定位过程中依然存在严重的漂移现象,定位精度仍然很低。
UWB (Ultra-Wideband,超宽带无线通信技术)具有抗干扰能力强、测距精度高、抗多径及穿透性强等优点[7],已经被应用于采煤机定位,刘清和王雪松等[8-9]提出基于超宽带测距原理的采煤机定位系统,并在井下进行了测试。 FAN 等[10]提出了一种基于INS/UWB 的采煤机动态定位方法,将UWB 安装在液压支架上,用来消除惯性导航系统累积的误差以提高定位精度。 王世博等[11]提出将UWB 基站部署在巷道的煤壁上,利用UWB 定位系统对采煤机进行三维坐标校正。 刘万里等[12]提出一种基于UWB 采煤机绝对位置精确校准的方法,将UWB 传感器等间距固定在端头处的液压支架上及布置均匀布置在巷道中,由于非视距环境的影响,定位精度欠缺。 刘一鸣等[13]提出将UWB 基站安装在区段巷道的煤壁上,采用信息过滤算法、神经网络算法依次对定位数据进行处理的定位精度提升算法。 YANG等[14]建立了一种的采煤机SINS/UWB 集成定位系统,将UWB 基站安装在液压支架上,采用基于决策树容错模型的定位方法获得采煤机的位置坐标。 张子悦等[15]提出了多感知方式组合测量的采煤机位姿检测系统,在液压支架顶端和底端分别安装UWB基站,将UWB 定位终端、倾角传感器和寻北仪安装在采煤机机身上。 液压支架的频繁移动,使液压支架上的基站群坐标不断的改变,很难精确的获得移动后基站群的坐标,导致采煤机定位精度较低。 田野[16]提出将UWB 基站群部署在端头区段巷道中,将基站群分为迁移组和量测组,其中迁移组的测量模块需要根据工作面推进的距离人工移动所需的距离,量测组的测量模块对移动后的迁移组测量模块进行量测定位,需要对每个基站进行单独移动,然后在解算基站群的坐标,井下环境复杂多变,容易使基站群迁移后误差较大,进而影响UWB 系统的定位精度。
目前常用的定位方法主要有最小二乘算法[17]、Chan 算法[18]、Taylor 展开算法[19]等,然而常规算法在煤矿井下环境中很难获得满意的定位精度。 为提高定位精度,郭继坤等[20]提出UWB 技术和井下复合衰落信道模型,利用面积形心算法,将未知节点的空间位置约束在一个较小的区域内,然后利用Taylor 和Chan 氏算法进行定位,平均定位误差在0.5~1.5 m。 谢芝玉等[21]提出一种基于Taylor 级数展开的UWB 定位算法,定位误差为0.4 m 左右。 孙继平等[22]提出一种基于测距值二次重构的井下定位方法,利用卡尔曼滤波进一步优化定位精度,定位精度为0.891 m。 笔者[23]采用多维标定算法获得初始值,然后利用粒子群优化算法提高初始值的精度,进一步采用Taylor 展开算法获得较准确的定位结果。 李旭红等[24]采用最小二乘法获得初始坐标,然后无迹卡尔曼滤波进行平滑处理,提高了定位精度,虽然上述方法提高了UWB 的定位精度,但是定位误差较大,难以应用于采煤机定位。
为提高采煤机的定位精度,提出了基于UWB定位系统的端头校准方法,对采煤机在端头进行校准,结合基站群的迁移装置,每刀截割完成后,能够为下次定位做好准备;针对井下UWB 定位精度低的问题,提出基于最小均方误差准则(Minimum Mean Square Error Criterion, MMSEC)的收缩估计方法,并利用扩展卡尔曼滤波(Extended Kalman Filter,EKF)对定位结果进行平滑处理,提高位置估计精度,根据采煤机的截割工艺,利用移动平台模拟采煤机的运动,检验所提迁移策略及定位算法的有效性。
为实现对采煤机进行端头自动校准,提出了基于UWB 端头校准补偿惯性导航定位误差的方法。在综采工作面的两端头处分别设置UWB 定位系统,实现对采煤机上山和下山进行端头定位,为方便分析,只给出了一端的布局图,如图1 所示。 将定位终端模块安装在采煤机机身上,将UWB 基站群设置在综采工作面的端头位置,基站群安装在自制的支架上,通过设置步进电机的脉冲数使UWB 基站群沿着导轨进行整体迁移。 姿态传感器固定在UWB 支架上,能够获得基站群迁移后的姿态,利用蓝牙收发模块将姿态信息传送到上位机,根据每个基站的初始坐标、姿态信息及设定基站群迁移的距离,在上位机的解算系统中能够快速的获得基站群的坐标。 当采煤机上的定位终端模块运行到距离端头5~10 m 时,启动UWB 定位系统,根据双向飞行时间的测距原理,通过UWB 系统自组网的形式获得定位终端与UWB 基站群之间的距离,采用所提的算法求解采煤机的位置信息。 UWB 基站群在初始安装时,采用全站仪标定测量基站群的坐标,同时尽可能保证每个基站与定位终端形成视距环境,由于非视距环境对定位精度有很大影响。 当采煤机完成一刀截割之后,UWB 基站群在导轨上沿着进刀的方向迁移,UWB 基站群可以在采煤机割完两刀或者多刀之后进行迁移,但是容易导致基站群与定位终端处于非视距环境中,非视距换对UWB 信号的传播影响较大,将导致定位精度较差。 因此采用“一刀一迁移”的方式进行定位,迁移距离与进刀量尽可能相等,有利于保持定位终端与基站群初始的视距环境不变。 基站群进行多次迁移后,可以重新标定基站群的坐标。 无论采煤机在上山还是下山,均可采用“一刀一迁移”的方式获得采煤机的位置,为惯性导航系统提供校准的基准。

图1 采煤机端头定位系统示意
Fig.1 Schematic of shear end positioning system
在UWB 定位系统中,根据定位终端与4 个基站之间的测量距离,建立如下观测方程组:

式中:dk,1, dk,2, dk,3, dk,4分别为在k 时刻定位终端与4 个基站之间的距离;nk,1, nk,2, nk,3, nk,4分别为高斯白噪声;(x1, y1, z1), (x2, y2, z2), (x3, y3,z3), (x4, y4, z4)为4 个UWB 基站的坐标,(x, y,z)为定位终端的坐标。 忽略测量噪声,式(1)两边平方,整理得:
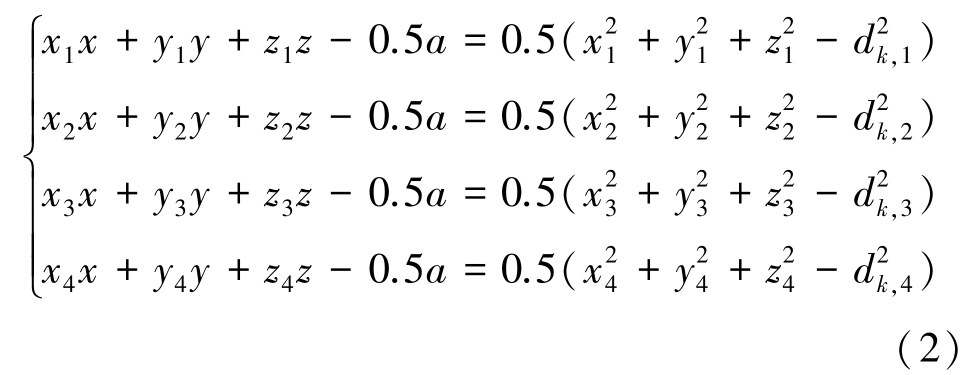
其中:a =x2 +y2 +z2。
将式(2)转换成矩阵形式:
其中,

式(3)的加权最小二乘解为
则有:
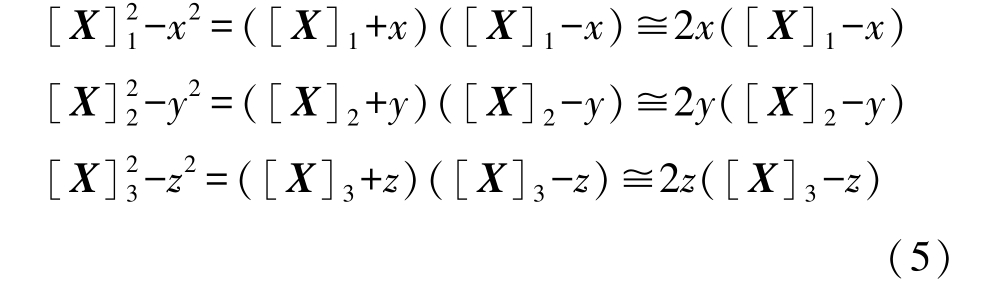
其中:[X]i为矩阵X 的第i 项,i=1, 2, 3。
将式(5)转换成矩阵形式:
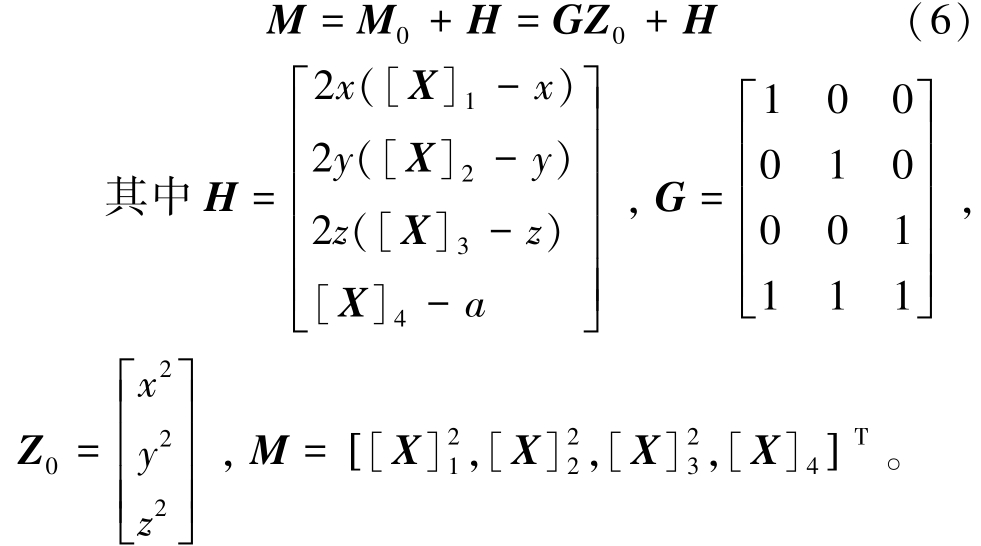
式(6)的最小二乘解为:
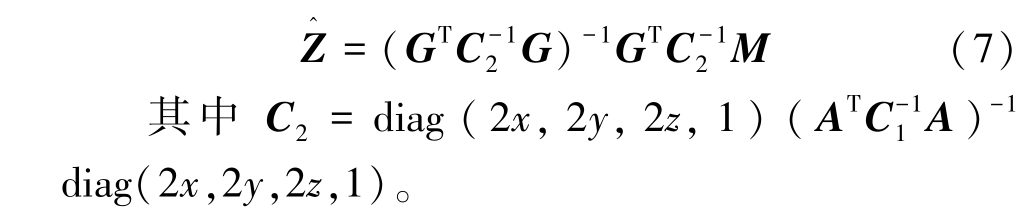
则定位终端的坐标为:

根据式(8)可求得定位终端的坐标,但是在井下复杂的环境中,测量噪声较大,将导致TOA 算法的定位精度较低。 为改善定位精度,采用基于最小均方误差准则的方法提高TOA 算法的估计精度,其均方误差表示为:

为使均方误差获得最小,对式(9)求导并令其求导后的因式等于零,整理可得:

根据式(6)和式(4)可进一步得到误差的估计值,即:

根据式(14),则有:
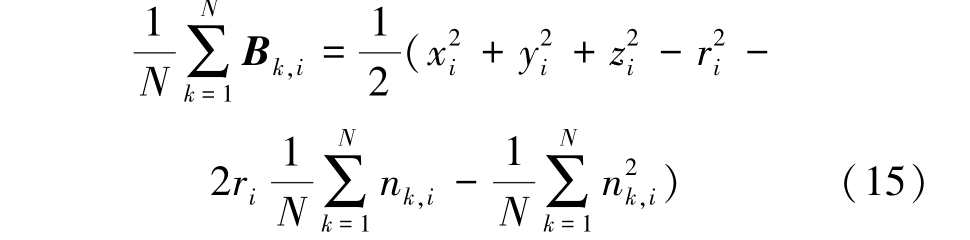
根据式(15),可计算期望为:
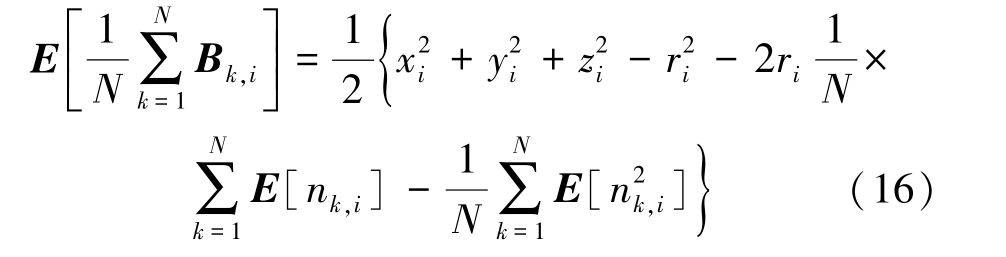
根据式(16),进一步可求得:
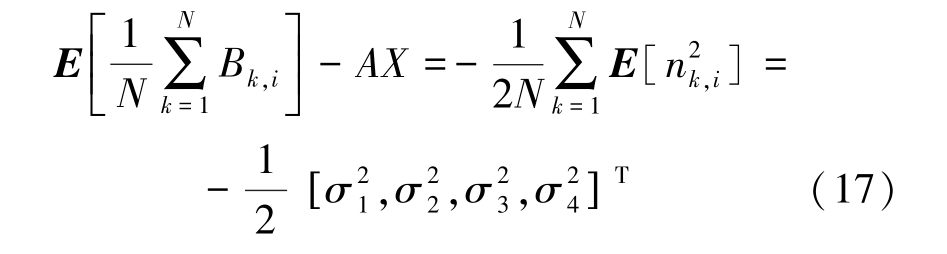
根据式(12)和式(17),可计算出误差的期望,如下:
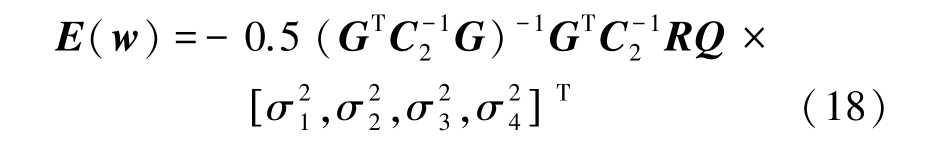
进一步可以计算误差的协方差为:
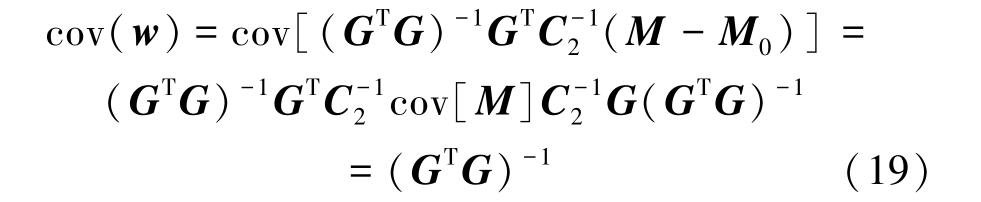
根据式(18)和式(19),可求得:
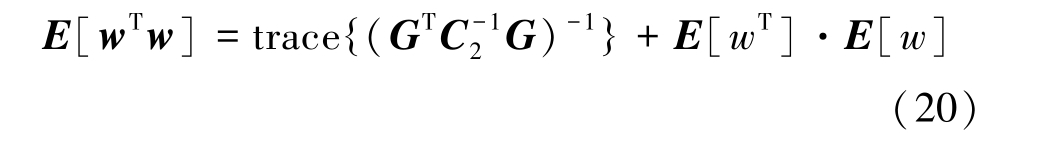
将式(18)和式(20)计算的值代入式(11),解算出收缩因子,则基于MMSEC 收缩估计的定位终端坐标表示为:
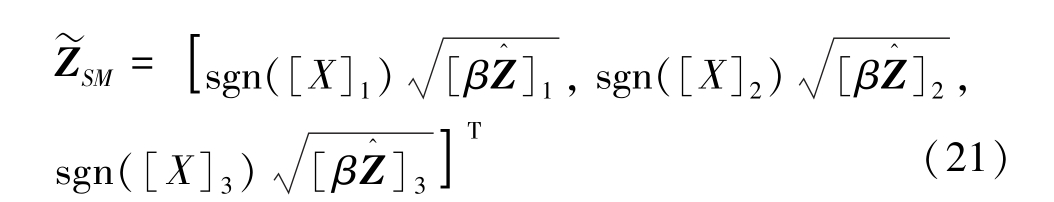
由于MMSEC 收缩估计并未消除测距误差对定位精度的影响,其定位结果依然具有较大的误差,需要对定位终端的坐标估计值进行进一步的优化。EKF 在定位系统中有着广泛的应用,因此采用EKF对定位结果进行滤波处理,提高定位精度。 定位终端在k+1 时刻的状态向量可表示为:

定位终端的状态方程构建为:
其中
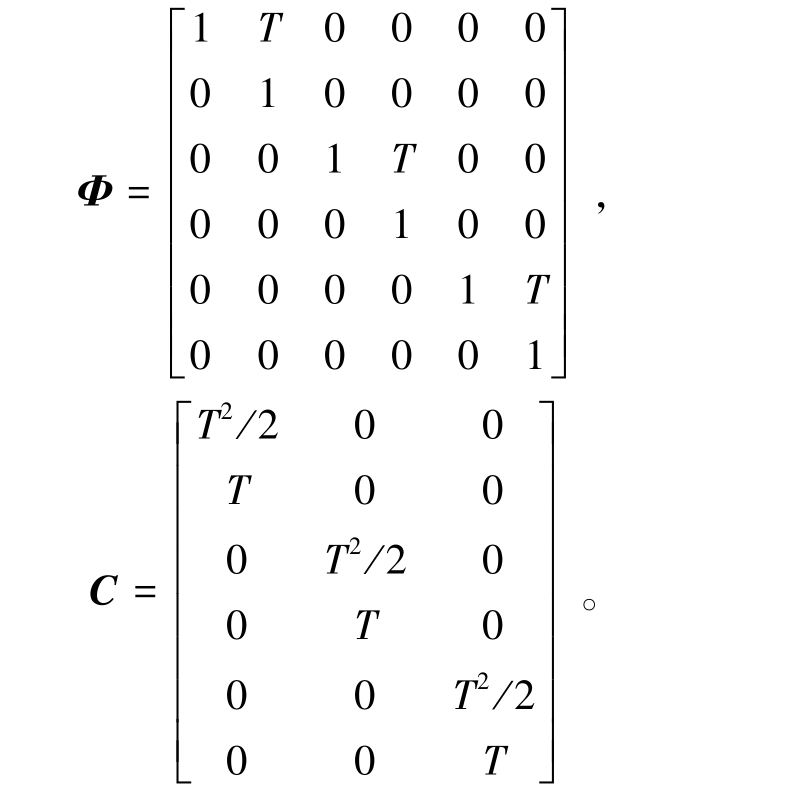
以定位终端与每个UWB 基站之间的距离建立观测方程,如下:
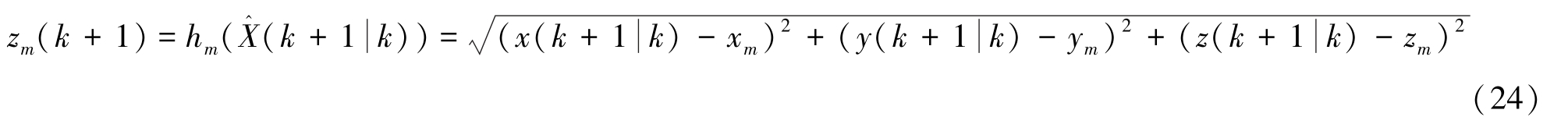
其中(xm,ym, zm)为第m 个基站的坐标,m=1,2,3,4,对观测方程进行一阶泰勒级数展开,忽略二次项以上余项,可得k+1 时刻的雅克比矩阵H,如下:
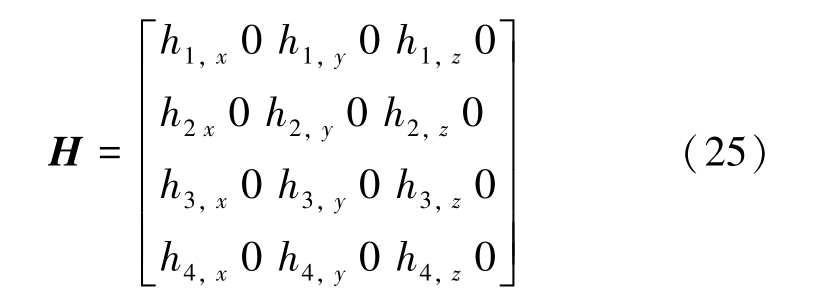
其中,

EKF 的主要步骤如下:
1) 预测:
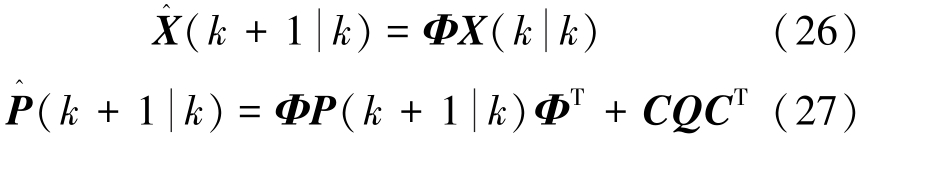
2) 更新:

利用上述EKF 对定位终端的位置实时预测更新,实现对基于最小均方误差准则的收缩估计的结果进行实时平滑,进一步消除距离残差对定位精度的影响,提高定位终端的位置估计精度。
姿态传感器输出的信息是基于载体坐标系的姿态,载体坐标系固定在基站群支架的质心上, 而解算移动后基站群的位置坐标是基于地理坐标系,地理坐标系指的是当地导航坐标系,三个坐标轴分别指向东向、北向和天向。 在整个试验中,解算的位置坐标都是在导航坐标系下进行的,将UWB 坐标系作为导航坐标系,以基站群的迁移方向为x 轴,定位终端的移动方向为y 轴,竖直向上的方向为z 轴。
根据上述“一刀一迁移”的策略,采煤机完成一刀截割后,UWB 基站群根据预先设置的距离在导轨上沿着进刀方向进行迁移,为下一刀的端头定位做好准备。 假设基站群在导轨上移动的距离为s, 姿态传感器在导轨上位移增量为ΔSb ,基站群在导航坐标系下的位移增量ΔSn ,其关系为:
式中,U 为姿态传感器输出的姿态矩阵,如下:

其中,
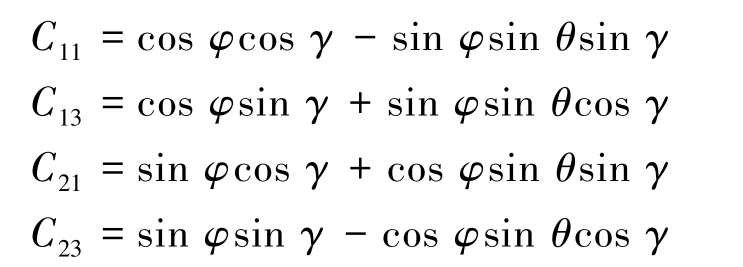
式中:φ 为航向角;θ 为俯仰角; γ 为横滚角。
将式(32)代入式(31),可得:
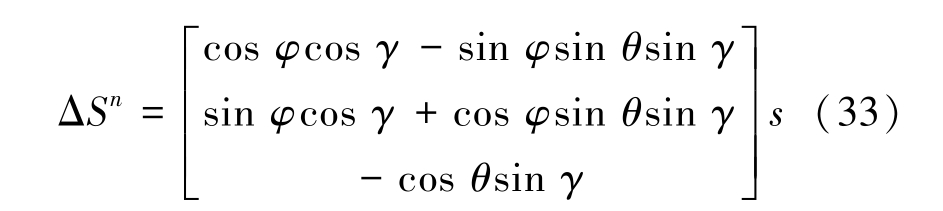
考虑到综采工作面端头路面不平整引起基站群移动前后姿态角发生变化,假设UWB 基站群的初始坐标为Pi(0) =(xi,yi,zi),迁移N 次之后,基站群的坐标为:
式中:Pi(N)为基站群迁移N 次后的坐标(i=1,2,3,4)。
为评价上述基站群迁移策略及所提算法的定位性能,采用均方根误差(RMSE)作为定位精度的评价指标,如下:
式中,(xr,yr,zr) 为定位终端在导航坐标系的真实坐标,(xt,yt,zt) 为上述算法解算出的导航坐标下的位置坐标;为了对比分析误差在3 个坐标轴上的变化情况,在导航坐标下x, y, z 轴上的误差为:

为验证所提方法的准确性和有效性,所有的基站及定位终端,均使用Time Domain 公司生产的UWB P440 模块。 将4 个UWB 基站安装在UWB 支架上,调整UWB 基站的相对位置,使4 个基站在水平面的投影为V 型,这种部署方式能够获得较好的定位精度[25]。 将蓝牙姿态传感器固定在UWB 支架上,获取基站群迁移后姿态角。 定位终端模块安装在移动平台上,模拟采煤机的运动,如图2 所示,设置定位终端的移动速度为0.1 m/s,假设采煤机每次的进刀量为0.8 m, UWB 基站群每次的迁移距离为0.8 m, 第1 刀截割时,4 个基站的坐标分别为AN1 (0.131,0.126 ,0.636), AN2 (1.283, 1.131,0.944), AN3 (- 0. 732, 1. 581, 1. 117), AN4(0.104, 0.226, 2.094),每刀截割完成后,根据基站群迁移的距离,分别解算每个UWB 基站的坐标。

图2 模拟采煤机运动的试验装置
Fig.2 Experimental device for simulating the shear movement
首先验证基于MMSEC 收缩估计的有效性,图3和图4 分别给出了定位误差变化曲线及三个坐标轴上的误差分布曲线。 从图3 可以看到,基于MMSEC收缩估计方法明显优于TOA 定位算法,使用MMSEC 收缩估计方法能够有效减小定位终端坐标的误差,提高UWB 系统的定位精度,尤其是当定位终端靠近基站群时,定位精度显著提升。 通过图4可知,MMSEC 收缩估计方法能显著减小x 轴和y 轴方向的误差,z 轴方向误差对MMSEC 收缩估计方法不敏感。

图3 TOA 算法和MMSEC 算法的定位误差变化
Fig.3 Variation of localization errors with respect to TOA and MMSEC method
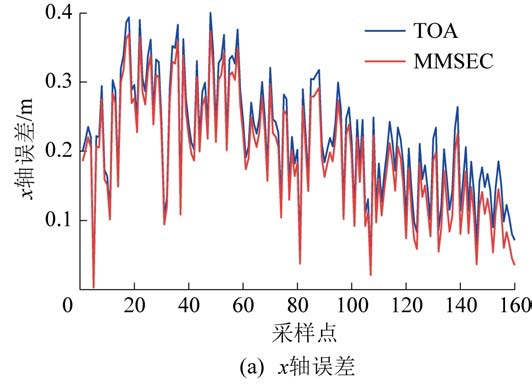

图4 TOA 算法和MMSEC 算法定位误差在3 个坐标轴的分布
Fig.4 Localization errors distribution on three axes regarding TOA and MMSEC method
为验证采煤机完成一次截割,部署在巷道中的UWB 基站群沿着导轨迁移一次的循环定位策略,根据第2 节所提的定位方法,计算UWB 基站迁移后每刀的独立误差。 图5 给出了截割5 刀的独立误差变化曲线,表1 给出了每刀截割过程中的最大误差、最小误差及平均误差。 通过对比可知,MMSEC 收缩估计方法能够改善每一刀运动轨迹的定位精度,尤其是第4 刀和第5 刀的定位精度提升比较明显。 第4 刀的平均定位误差由0.341 m 减小为0.296 m,定位精度提升了13.1%;第5 刀的平均定位误差由0.394 m减小为0.339 m,定位精度提高了13.9%。使用EKF 对MMSEC 的结果进行平滑处理,进一步消除了距离残差对定位精度的影响,使每一刀截割的平均定位误差进一步减小,第4 刀和第5 刀的平均定位精度再次提升13.5%和10.6%。 随着循环截割刀数的增加,定位误差逐渐增大,尽管UWB 定位系统不存在误差累积现象,但是在解算迁移后的UWB 基站坐标时,需要结合姿态传感器的姿态角,姿态传感器随时间存在漂移现象,对比第4 刀和第5 刀的误差,第5 刀最大误差明显增加,TOA 算法由0.37 m变为0.565 m, MMSEC 算法由0.325 m 变为0.544 m, MMSEC-EKF 算法由0.340 m 变为0.409 m。 因此在移动UWB 基站群时,应尽可能快速的完成迁移任务,缩短基站群的迁移时间,减小姿态传感器的漂移,提高UWB 基站群的位置估计精度。MMSEC-EKF 算法的前3 次循环截割的定位精度小于0.2 m, 能够为惯性导航定位系统提供相对准确校准基准,为此采煤机完成3 次循环截割后,重新测量每个基站的坐标,有利于获得更高的定位精度。
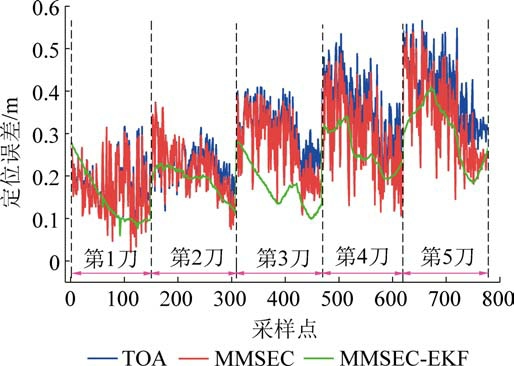
图5 不同算法的定位误差变化
Fig.5 Variation of localization error under different positioning algorithms
表1 循环截割定位误差对比
Table 1 Comparison positioning error of cyclic cutting

定位算法 刀数 最大误差/m最小误差/m平均误差/m TOA第1 刀 0.316 0.046 0.179第2 刀 0.372 0.126 0.231第3 刀 0.408 0.155 0.297第4 刀 0.370 0.222 0.341第5 刀 0.565 0.227 0.394 MMSEC第1 刀 0.312 0.021 0.169第2 刀 0.370 0.075 0.213第3 刀 0.391 0.108 0.265第4 刀 0.325 0.181 0.296第5 刀 0.544 0.145 0.339第1 刀 0.273 0.058 0.145 MMSEC-EKF第2 刀 0.229 0.11 0.189第3 刀 0.280 0.098 0.173第4 刀 0.340 0.192 0.256第5 刀 0.409 0.184 0.303
为进一步分析UWB 基站群迁移后,循环定位过程中3 个坐标轴独立误差的变化情况,图6 给出了误差在x,y,z 三个轴上的分布曲线,表2 给出了三个坐标轴的平均误差。 结果表明,在每刀截割过程中,y 轴误差小于x 轴误差和z 轴误差,说明采煤机沿着截割方向误差较小,精度相对较高;使用MMSEC 收缩估计算法后x 轴和y 轴方向误差明显减小,z 轴方向误差变化不明显;经过EFK 平滑后,x轴和z 轴方向的误差进一步减小,使得MMSECEKF 算法能够获得较高的定位精度。 对比发现,MMSEC-EKF 算法的前3 刀定位误差较小,3 个坐标轴的误差相对较小,能够满足井下定位的要求。值的注意的是第2 刀的y 轴误差略大于第3 刀y 轴误差,这是由于路面不平整,导致定位终端移动平台振动更加严重引起截割方向的误差增大。
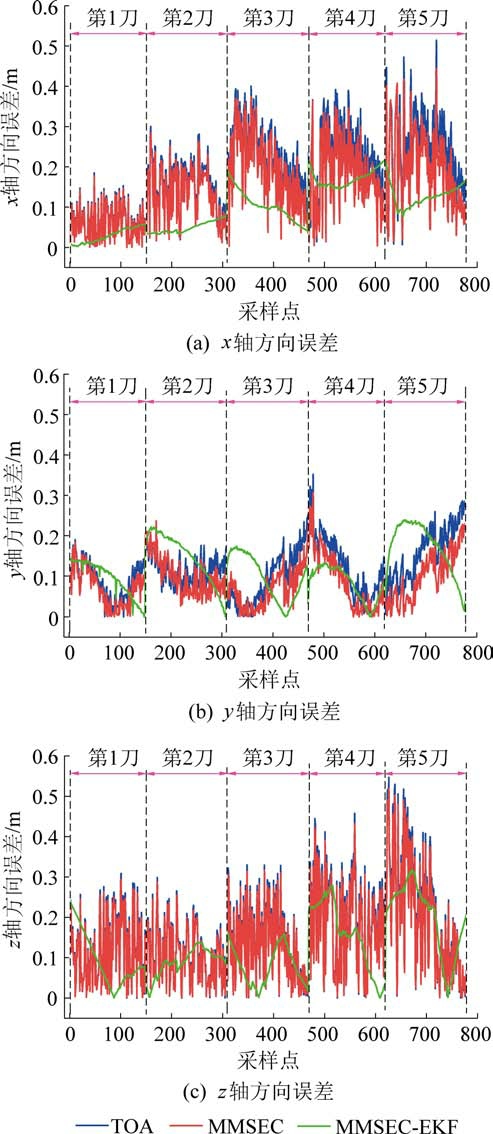
图6 循环截割误差在3 个坐标轴的分布
Fig.6 Errors distribution of cyclic cutting on three coordinate axes
由表2 可知,随着基站群迁移次数的增加,在循环截割过程中,3 种算法的x 轴和z 轴平均误差逐渐增加,y 轴平均误差基本保持在0.2 m 之内;x 轴和z轴方向的误差存在波动较大,这是由于UWB 基站群随迁移次数的增加,导致基站群的坐标误差增加所致,另一方面是由于定位终端在运行过程中存在着振动。 UWB 基站群迁移3 次时,误差相对较小,尽管有某个点的误差偏大,但总体来看,前3 刀的精度基本能够满足定位的要求。 在井下实际应用环境中,实施“一刀一迁移”的端头定位策略,UWB 系统的定位精度可能受到井下的水雾、粉尘及采煤机振动的影响,需要进一步深入研究。
表2 3 个坐标轴上的平均误差
Table 2 Average positioning errors on three axes

定位算法 刀数 平均误差/m x 轴 y 轴 z 轴第1 刀 0.061 0.088 0.120 TOA第2 刀 0.146 0.116 0.106第3 刀 0.218 0.092 0.134第4 刀 0.213 0.128 0.1944第5 刀 0.241 0159 0.206第1 刀 0.057 0.071 0.114 MMSEC第2 刀 0134 0.101 0.111第3 刀 0.195 0.066 0.127第4 刀 0.181 0.091 0.182第5 刀 0.196 0.101 0.195第1 刀 0.029 0.093 0.092 MMSEC-EKF第2 刀 0.049 0.146 0.089第3 刀 0.102 0.096 0.078第4 刀 0.171 0.082 0.156第5 刀 0.182 0.170 0.196
1)为精确获得采煤机在端头的位置坐标,提出了“一刀一迁移”的定位策略,可代替传统的人工校准,能够实现连续循环截割,节省了端头停机校准的时间,提高了生产率。
2)考虑到井下实际环境中测量噪声较大,提出了基于MMSEC 的TOA 收缩估计方法,进而采用EKF 对定位结果进行平滑处理,进一步消除距离残差对定位精度的影响。 试验结果表明,MMSEC 收缩估计方法能够提高运动轨迹的定位精度,第4 刀和第5 刀的定位精度提升比较明显,平均定位误差由0.341 m,0.394 m 减小为0.296 m,0.339 m,定位精度分别提升了13.1%和13.9%,经过EKF 平滑处理后,第4 刀和第5 刀的平均定位精度进一步提升13.5% 和10.6%,证明了所提的定位方法能有效地提高UWB 定位系统的精度。
3) 随基站群迁移次数的增加,平均定位误差逐渐增大,x 轴和z 轴平均误差逐渐增加,y 轴平均误差基本保持在0.2 m 之内,MMSEC-EKF 算法的前3刀的定位精度小于0.2 m, 因此采煤机完成3 次循环截割后,重新测量基站群的坐标,能够获得更好的定位效果;提出的端头“一刀一迁移”的定位策略及定位算法为井下定位技术提供理论参考,该方法有待井下环境的进一步试验验证。
[1] 葛世荣,郝尚清,张世洪,等.我国智能化采煤技术现状及待突破关键技术[J]. 煤炭科学技术, 2020, 48(7):28-46.GE Shirong,HAO Shangqing, ZHANG Shihong,et al.Status of in⁃telligent coal mining technology and potential key technologies in China [J]. Coal Science and Technology, 2020, 48 (7):28-46.
[2] 刘万里,张学亮,王世博. 采煤工作面煤层三维模型构建及动态修正技术[J]. 煤炭学报, 2020, 45(6):1973-1983.LIU Wanli,ZHANG Xueliang ,WANG Shibo. Modeling and dy⁃namic correction technology of 3D coal seam model for coalmining face [J]. Journal of China Coal Society, 2020, 45(6):1973-1983.
[3] REID D C,DUNN M T,REID P B,et al.A practical inertial navi⁃gation solution for continuous miner automation [ J]. Coal Operators ’ Conference, University of Wollongong & the Australasian Institute,2012,12:114-119.
[4] 李 昂,郝尚清,王世博,等.基于SINS/轴编码器组合的采煤机定位方法与试验研究[J].煤炭科学技术,2016,44(4):95-100.LI Ang,HAO Shangqing,WANG Shibo,et al.Experimental study on shearer positioning method based on SINS and Encoder [J].Coal Science and Technology,2016,44(4):95-100.
[5] 张博渊,王世博,葛世荣.惯性导航初始对准偏差与安装偏差对采煤机定位精度影响及其校准方法[J].煤炭学报,2017,42(3):789-795.ZHANG Boyuan,WANG Shibo,GE Shirong.Effects of initial align⁃ment error and installation noncoincidence on the shearer positioning accuracy and calibration method [J].Journal of China Coal Society,2017,42(3):789-795.
[6] 鲁 程, 王世博, 葛世荣, 等. 多惯导冗余的采煤机定位原理及其合理性分析[J]. 煤炭学报, 2019, 44(S2):746-753.LU Cheng,WANG Shibo,GE Shirong,et al.Redundant multi-INS positioning algorithm of shearer and analysis of its rationality [J].Journal of China Coal Society,2019,44(S2):746-753.
[7] CAO B, WANG S, GE S, et al. Improving Positioning Accuracy of UWB in Complicated Underground NLOS Scenario Using Cali⁃bration, VBUKF, and WCA [J]. IEEE Transactions on Instru⁃mentation and Measurement,2021, 70:1-13.
[8] 刘 清. 基于超宽带技术的采煤机定位系统设计[J]. 煤炭科学技术,2016,44(11):132-135.LIU Qing.Design on positioning system of shearer based on ultra wide band technology[J].Coal Science and Technology,2016,44(11):132-135.
[9] 王雪松. 基于UWB 技术的采煤机位置监测系统[J].山西焦煤科技,2016, 40(9):4-6.WANG Xuesong. Position monitoring system of shearer based on UWB technology [J]. Shanxi Coking Coal Science & Technology,2016, 40(9):4-6.
[10] FAN Q, SUN B, SUN Y, et al. Data fusion for indoor mobile ro⁃bot positioning based on tightly coupled INS/UWB[J]. Journal of navigation, 2017, 70(5):1079-1097.
[11] 王世博,葛世荣,葛照亮,等. 融合地质环境信息的采煤机绝对定位装置与方法[P]. 中国专利,201310353737.7,2013-08-15.
[12] 刘万里,刘一鸣. 一种基于UWB 采煤机绝对位置精确校准的方法和装置[P].中国专利,201410749250.5, 2014-12-09.
[13] 刘一鸣, 刘万里, 张博渊, 等. 基于UWB 的采煤机定位精度提升算法研究[J]. 工矿自动化,2016, 42 (12):25-30.LIU Yiming, LIU Wangli, ZHANG Boyuan, et al. Research of precision improving algorithm of shearer positionning based on UWB [J]. Industry and Mine Automation, 2016, 42(12):25-30.
[14] YANG H, LUO T, LI W, et al. A Stable SINS/UWB Integrated Positioning Method of Shearer Based on the Multi-Model Intelli⁃gent Switching Algorithm [J]. IEEE Access, 2019, 7:29128-29138.
[15] 张子悦, 符世琛, 刘 超, 等. 基于多感知方式组合测量的采煤机位姿检测系统[J].煤炭科学技术,2021,49(11):218-224.ZHANG Ziyue,FU Shichen,LIU Chao, et al. Position detection system of shearer based on combined measurement of multiple sensing modes [J].Coal Science and Technology,2021,49(11):218-224.
[16] 田 野. 综采工作面采煤机超宽带定位系统研究[D].徐州:中国矿业大学,2018.TIAN Ye. Research on UWB positioning system of shearer in longwall mining workface [D]. Xuzhou:China University of Min⁃ing and Technology,2018.
[17] HUANG Z,LU J. Total least squares and equilibration algorithm for range difference location [J]. Electronics Letters, 2004,40(5):173-174.
[18] CHAN Y, HO K. A simple and efficient estimator for hyperbolic location [J]. IEEE Transactions on Signal Processing, 1994,42(8):1905-1915.
[19] ALAVI B,PAHLAVAN K.Modeling of the TOA-based distance mea⁃surement error using UWB indoor radio measurements [J]. IEEE Communications Letters,2006,10(4):275-277.
[20] 郭继坤,丁 龙. 矿井非视距环境下UWB 人员定位算法[J].黑龙江科技学院学报, 2013, 23(2):181-184.GUO Jikun, DING Long. Study on NLOS positioning using UWB in mines [ J ]. Journal of Heilongjiang Institute of Science&Technology, 2013,23(2):181-184.
[21] 谢芝玉, 刘雄飞, 胡志坤. 基于Taylor 展开的UWB 井下定位算法研究与实现[J].计算机工程与应用, 2017, 53 (2):231-235.XIE Zhiyu, LIU Xiongfei, HU Zhikun. Research and design of underground coal mine positioning method based on Taylor algo⁃rithm [J]. Computer Engineering and Applications, 2017,53(2):231-235.
[22] 孙继平,蒋恩松.基于测距值二次重构的弯曲巷道目标定位方法[J]. 煤炭学报,2018,43(1):287-294.SUN Jiping,JIANG Ensong. Target positioning method of curved roadways based on two-reconstructing ranging value [J]. Journal of China Coal Society, 2018, 43(1):287-294.
[23] CAO B,WANG S,GE,S,et al. Study on the improvement of ul⁃tra-wideband localization accuracy in narrow and long space [J].Sensor Review, 2019, 40(1) 42-53.
[24] 李旭虹,张同丽,张育英. 矿井NLOS 环境下改进UKF 超宽带定位算法[J]. 西安科技大学学报,2018, 38(5):824-829.LI Xuhong, ZHANG Tongli, ZHANG Yuying, Reasearch on im⁃proved UKF UWB localization algorithm in mine NLOS environ⁃ment [ J]. Journal of Xi’ An University of Science and Technology. 2018, 38(5):824-829.
[25] 成 龙,符世琛,王鹏江,等. 基于Chan 算法的掘进机超宽带位姿检测基站布局分析[J]. 煤炭技术, 2018, 37(8):278-280.CHENG Long, FU Shichen, WANG Peng, et al. Base station layout analysis of UWB pose detection for roadheader based on chan algorithm [J]. Coal Technology, 2018, 37(8):278-280.