
移动扫码阅读

移动扫码阅读
近年来,加筋土挡墙的使用范围越来越广泛,究其原因,主要是其结构刚度小、柔性大,设计方便,外形美观,节省造价且较实用[1-2]。李鸿强[3-5]等通过现场试验及模型试验研究了加筋土挡墙的性状。当前规范中大多是关于顺直加筋土挡墙设计方法的研究,对于挡土墙拐角部位的研究相对较少,且相应规范也不健全[6-7]。但在实际应用中挡土墙拐角部位变形较直线部位更为严重:刘晓明[8]在对于挡土墙形态与结构的研究中发现加筋土挡墙拐角部位的鼓胀病害的重要原因是拐角部位比直线部位更易变形。KI等[9]通过模型实验分析研究了挡土墙拐角部位的水平变形情况。ZHANG[10-12]在极限平衡理论基础上,通过改变参变量及材料特性研究三维斜坡稳定性受拐角区域的影响程度,并基于变分原理分析了凸形拐角的三维稳定性中的作用,次年在此基础上开发了计算其所需强度和加固长度的分析程序。工程上常常由于缺乏对挡墙拐角部位形态和结构特殊性的分析,出现施工方案错误,导致挡墙稳定性不足,变形过大,甚至破坏的结果。
为了完善加筋土挡墙拐角部位的结构设计、确保其安全性,基于山西其亚铝业有限公司2 400 000 t/a氢氧化铝及600 000 t/a高精铝板带箔项目,利用软件FLAC3D对不规则加筋土挡墙在3种影响因素下的土工格栅拉应力变形特征进行数值分析研究,旨在减小土工格栅的破坏程度从而提高挡墙的稳定性。
项目位于暂时性线状水流侵蚀作用形成的沟谷内,属于典型的黄土高原上的地貌形态。边坡采用多级台阶式加筋土挡墙,单级墙高均为10 m,平台宽4 m,平台上设置浆砌片石排水沟,喷射砼护面。挡墙拐角部位墙面内夹角设置为90°~150°,面板仰角为90°,面板通过反包式墙面与钢筋混凝土整体浇筑平衡墙后土体压力。筋材采用GSZ型双线黏结焊接、双向钢塑土工格栅,填料采用砂性土,压实系数λc=0.94。为使地基更加稳固,对原土地基进行平整,利用锤击将钢管打入土中,使之侧向挤密成孔,将管拔出去后,在桩孔中分层回填2∶8灰土夯实而成;为避免不均匀沉降的发生,在施工的过程中,采用大范围碎石、砂掺水泥刚性基础。
相关研究表明面板对加筋土挡墙整体稳定性的影响较小[13-15],故本次研究采用简化的模型,不考虑面板单元的影响,不考虑填土的差异分析加筋土挡墙拐角部位土工格栅最大拉应力分布规律。几何模型为单级直立式加筋土挡墙,墙面内夹角为90°,长宽度30 m,高度10 m,地基有1 m的埋置深度。挡墙底部设置竖向约束,拐角部位设置水平约束,墙面为了模拟临空状态不设置约束。
FLAC3D软件中Geogrid单元表现为一种线弹性材料,具有抗拉而不能抗压的特性。使用Geogrid单元模拟土工格栅,其长度为7 m(0.7H,H为墙高),竖向间距为0.5 m,共铺设19层(图1)。

图1 土工格栅布设
Fig.1 Geogrid laying schematic
挡墙填土和地基均采用摩尔库伦本构模型,挡墙填土为砂性土,不考虑地基变形对挡墙的影响。根据工程材料技术参数及相关要求,表1、表2分别为挡墙填土与地基参数及土工格栅参数。
表1 挡墙填土与地基参数
Table 1 Parameters of retaining wall filling and foundation

分组容重γ/(kN·m-3)弹性模量E/MPa体积模量K/MPa剪切模量G/MPa黏聚力C/kPa内摩擦角φ/(°)泊松比填土195042195350.3地基251 00056042500400.2
表2 筋材参数
Table 2 Parameters of reinforcement

参数弹性模量/MPa泊松比土工格榻厚度/mm耦合弹簧黏聚力/kPa耦合弹簧摩擦角/(°)单位面积耦合弹簧的刚度/MPa取值24 0000.3322.53050
为分析土工格栅的受力情况,研究使用FLAC3D软件中的Geogrid单元分析土工格栅最大主应力,因模拟的土工格栅只有受拉的特性,故土工格栅最大主应力为最大拉应力。
图2为土工格栅拉应力分布(包括整体和顶层)。由整体土工格栅拉应力分布图2a可知:①土工格栅最大拉应力在A处最大,即墙高中下部的拐角部位数据较大;②由顶层土工格栅拉应力分布图2b可知:距离墙面较远处的拐角部位拉应力最大(即B处),格栅拉应力沿着墙面的拐角部位的连线呈对称分布,并呈现“X”形状。
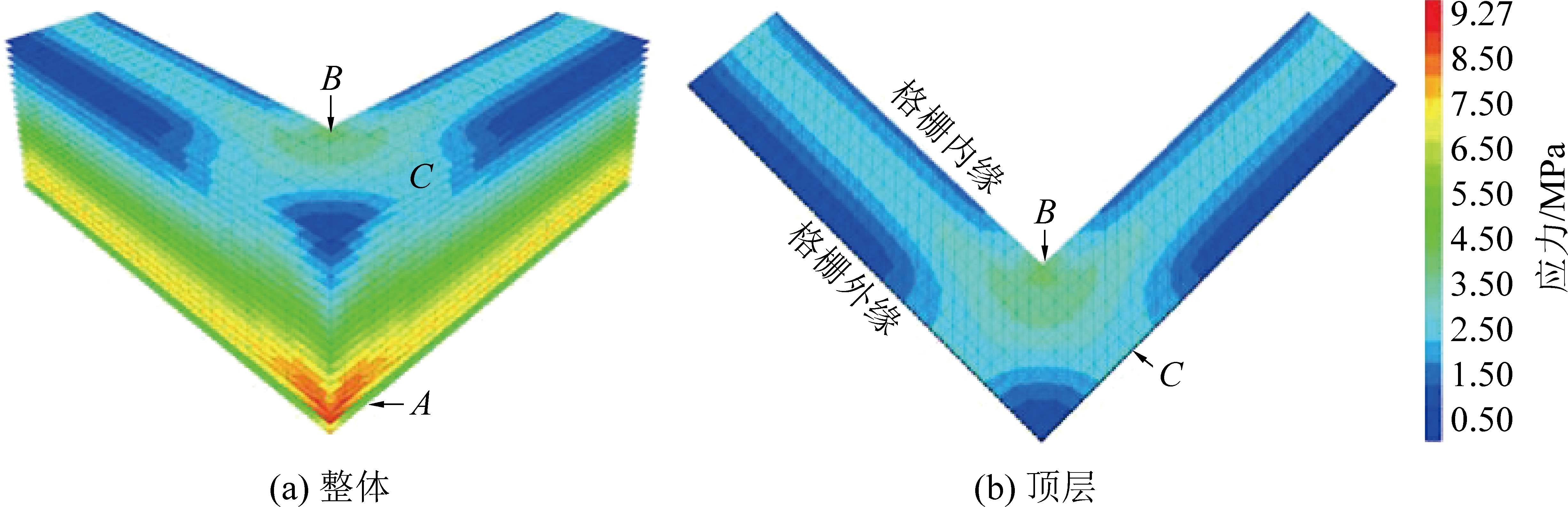
图2 整体和顶层土工格栅拉应力分布
Fig.2 Tensile stress distribution of overall and top geogrid
由顶层土工格栅外缘的最大拉应力分布规律(图3)可知:在C处(过渡区域)拉应力值最大,整体近似正态分布。
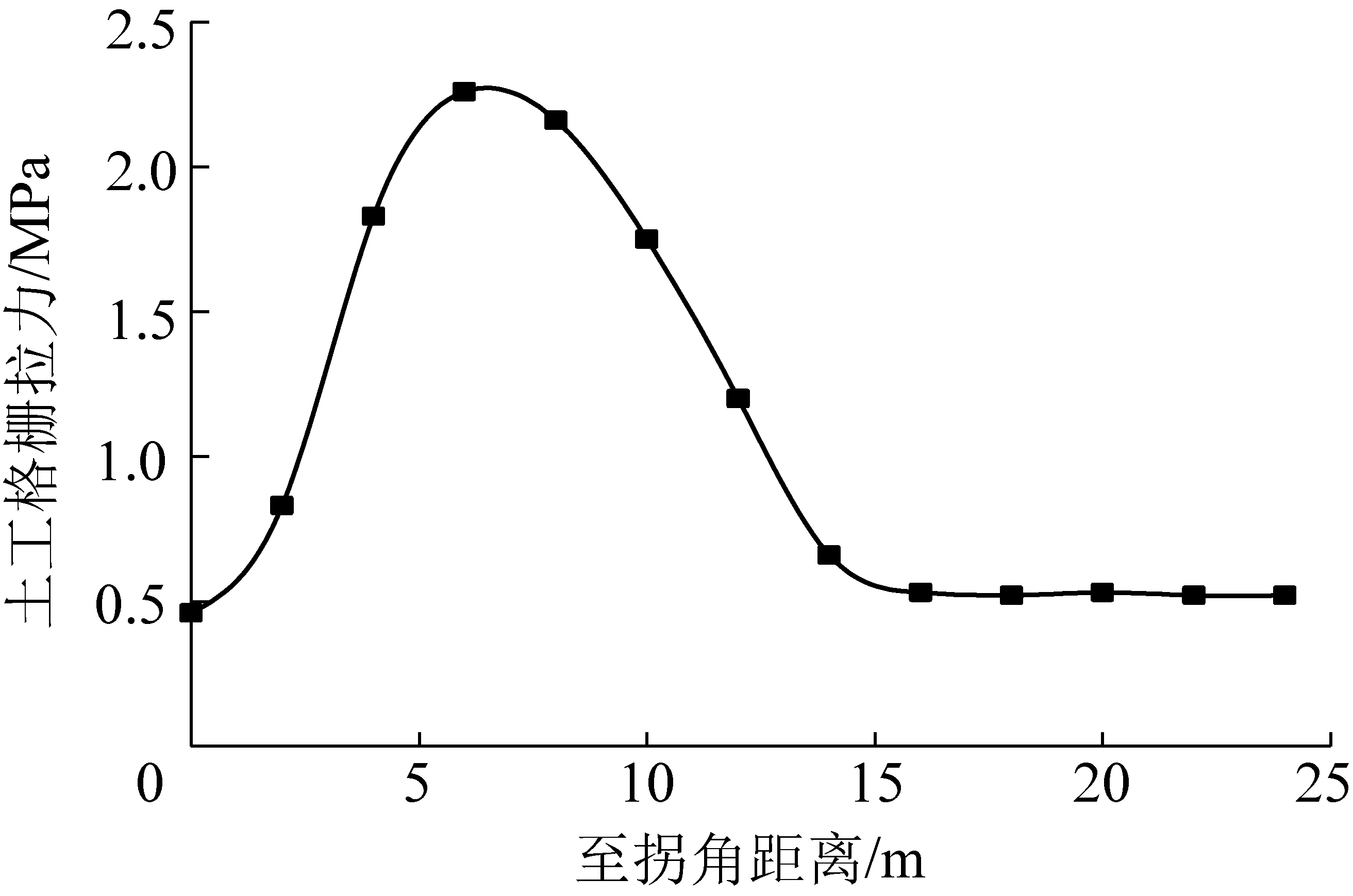
图3 土工格栅外缘拉应力分布曲线(顶层)
Fig.3 Outer edge tensile stress distribution curve (top geogrid)
图4为拐角和直线部位顶层土工格栅在剖面处的拉应力分布曲线,距墙面0~2 m时拐角部位和直线部位土工格栅拉应力变化规律一致,2 m后拐角部位呈现与直线部位明显的区别。
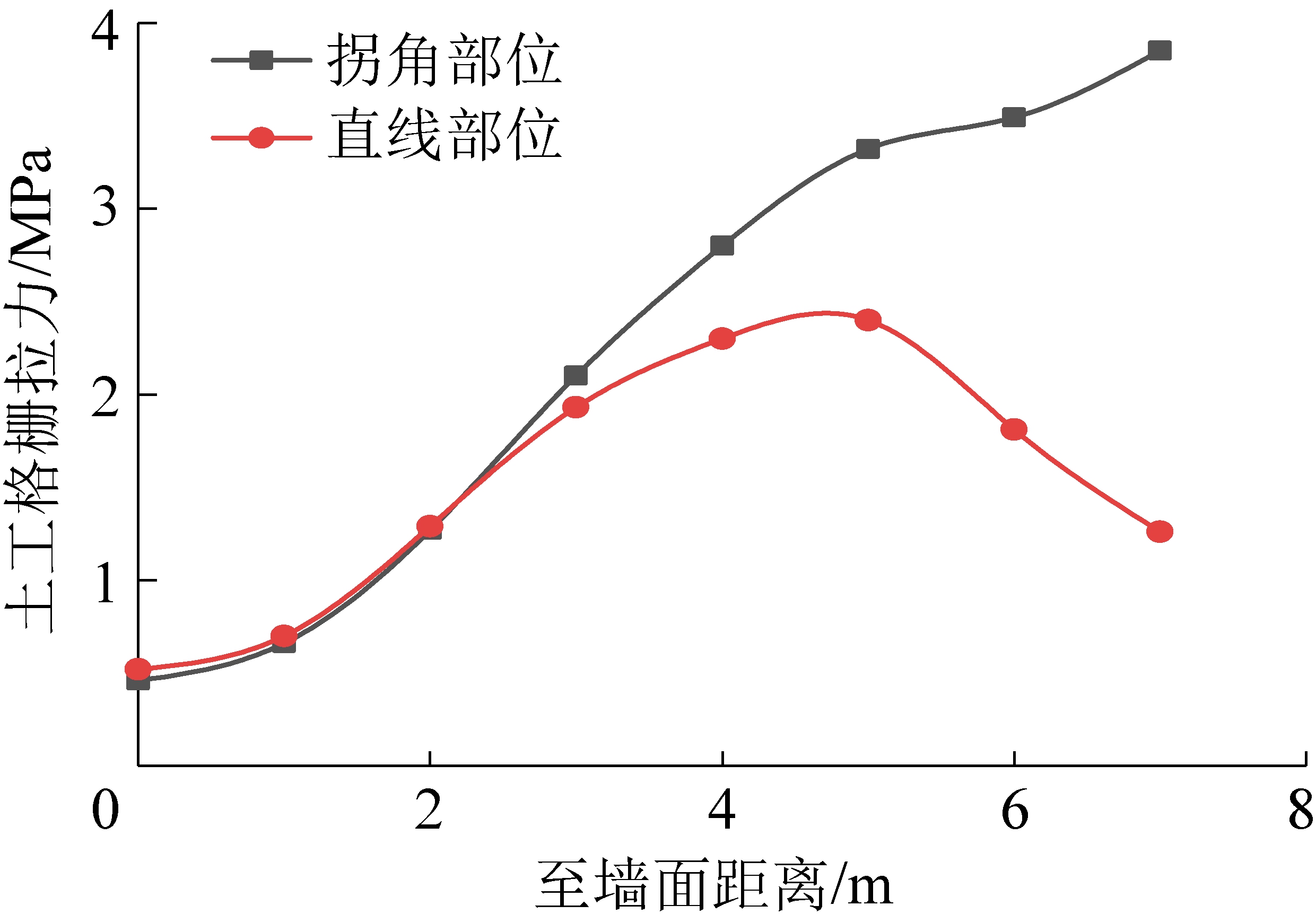
图4 拐角和直线部位顶层格栅拉应力分布曲线(剖面)
Fig.4 Top geogrid tension stress distribution curve (sections of corners and straight part)
通常认为筋材间距是加筋效果的一大重要指标,间距越小则加筋效果越好,但间距过小易造成“超筋土”,不仅造价昂贵、施工复杂而且加筋效果也不明显,因此合理控制筋材间距,不仅能使筋材充分发挥其作用起到控制变形的效果而且还能降低相应成本。研究认为加筋土挡墙筋材间距一般不大于800 mm[17]。
为研究筋材间距对加筋土挡墙顶层土工格栅拉应力的影响,在FLAC3D中建立筋材间距分别为0.1、0.3、0.5、0.7 m的加筋土挡墙拐角部位三维模型。土工格栅铺设长度7 m,土工格栅抗拉强度、填土和地基强度参数同上。
图5为土工格栅拉应力分布图和顶层土工格栅拉应力分布图(以筋材间距0.3 m为例)。拐角部位土工格栅拉应力分布规律与直线部位有明显区别。将各筋材间距大小的顶层土工格栅边线上的拉应力数据绘制如图6所示:边线上的土工格栅拉应力受加筋间距的影响较大,筋材间距与土工格栅拉应力存在正相关关系,即筋材间距越小,土工格栅拉应力越小,同等拉力下相应的破坏范围越小,这与栾茂田和外国学者LESHCHINSKY通过FLAC程序研究改变筋材间距是如何影响加筋土挡墙的稳定性的研究结果一致,即加筋土挡墙发生破坏的可能性与筋材间距成正比[18-19];间距小于0.3 m时实际的加筋效果并不比间距0.3 m时明显,不但经济上不合理,还增大施工难度,即筋材间距最小为0.3 m时最佳;随着距拐角距离(0~15 m)的增大土工格栅拉应力出现先增后减趋势,6 m处达到最大;15 m后变化较小,这与直线型加筋土挡墙规律相同[20-23]。

图5 加筋间距0.3 m土工格栅拉应力分布
Fig.5 Geogrid tensile stress distribution of tensile spacing 0.3 m
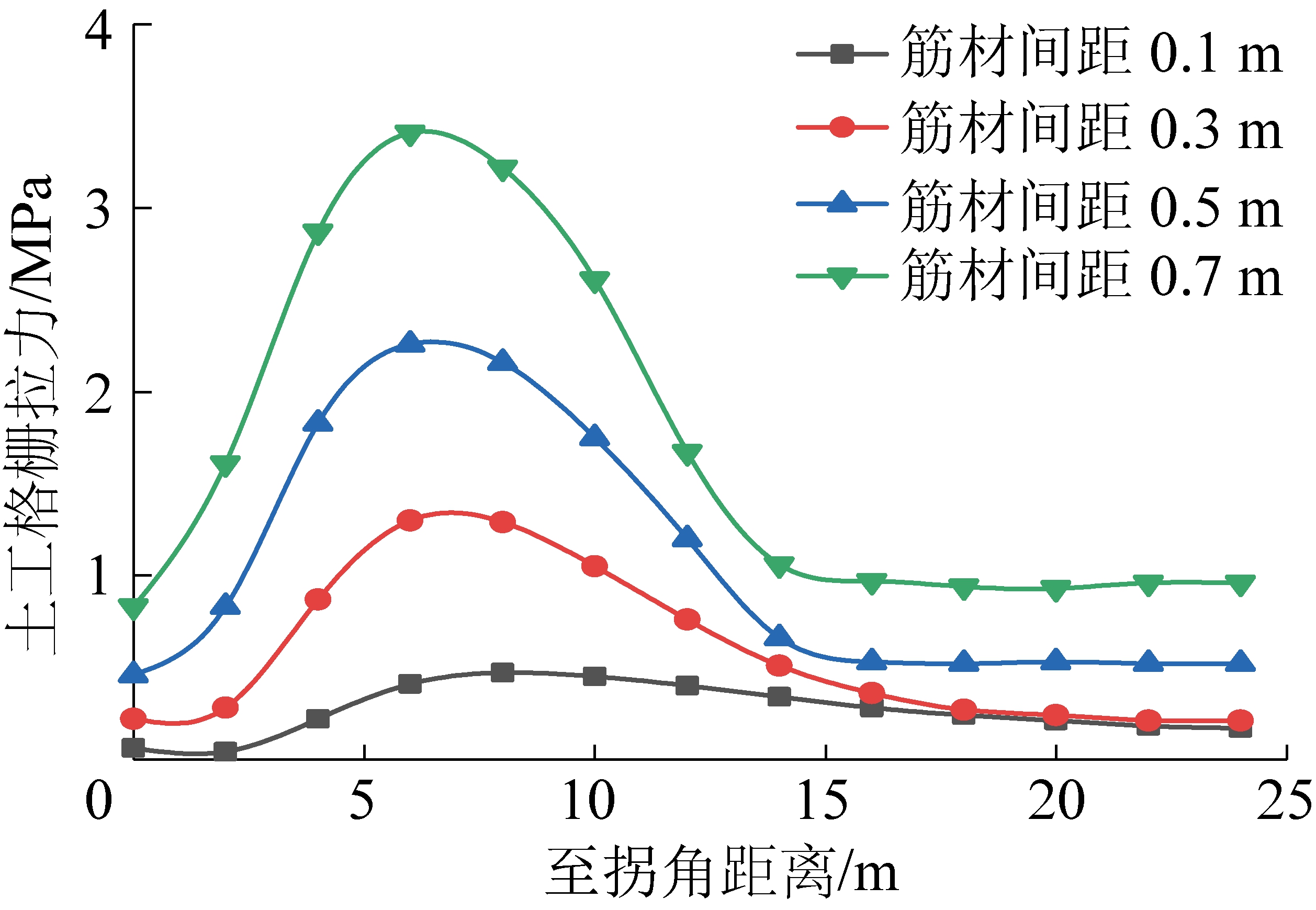
图6 土工格栅外缘拉应力分布曲线(加筋间距影响)
Fig.6 Outer edge tensile stress distribution curve (reinforcement spacing)
图7为拐角和直线部位在剖面处顶层格栅拉应力受筋材间距影响的分布曲线。筋材间距越大,土工格栅拉应力越大,拐角平分线上相应的破坏范围越大。当筋材间距等于0.3 m时,随着距墙面距离的增大,拐角部位与直线部位的土工格栅拉应力的差异减小,即拐角部位的变形程度减弱,挡墙的稳定性提高;小于0.3 m时加筋效果不明显,故为合理地控制挡墙变形可将筋材最小间距设置为0.3 m。格栅最大拉应力分布规律在拐角部位与直线部位明显不同,在拐角部位,格栅最大拉应力与距墙面的距离呈正比例关系;在直线部位随着距墙面距离的增大出现先增后减趋势,距墙面4~6 m的位置达到峰值。
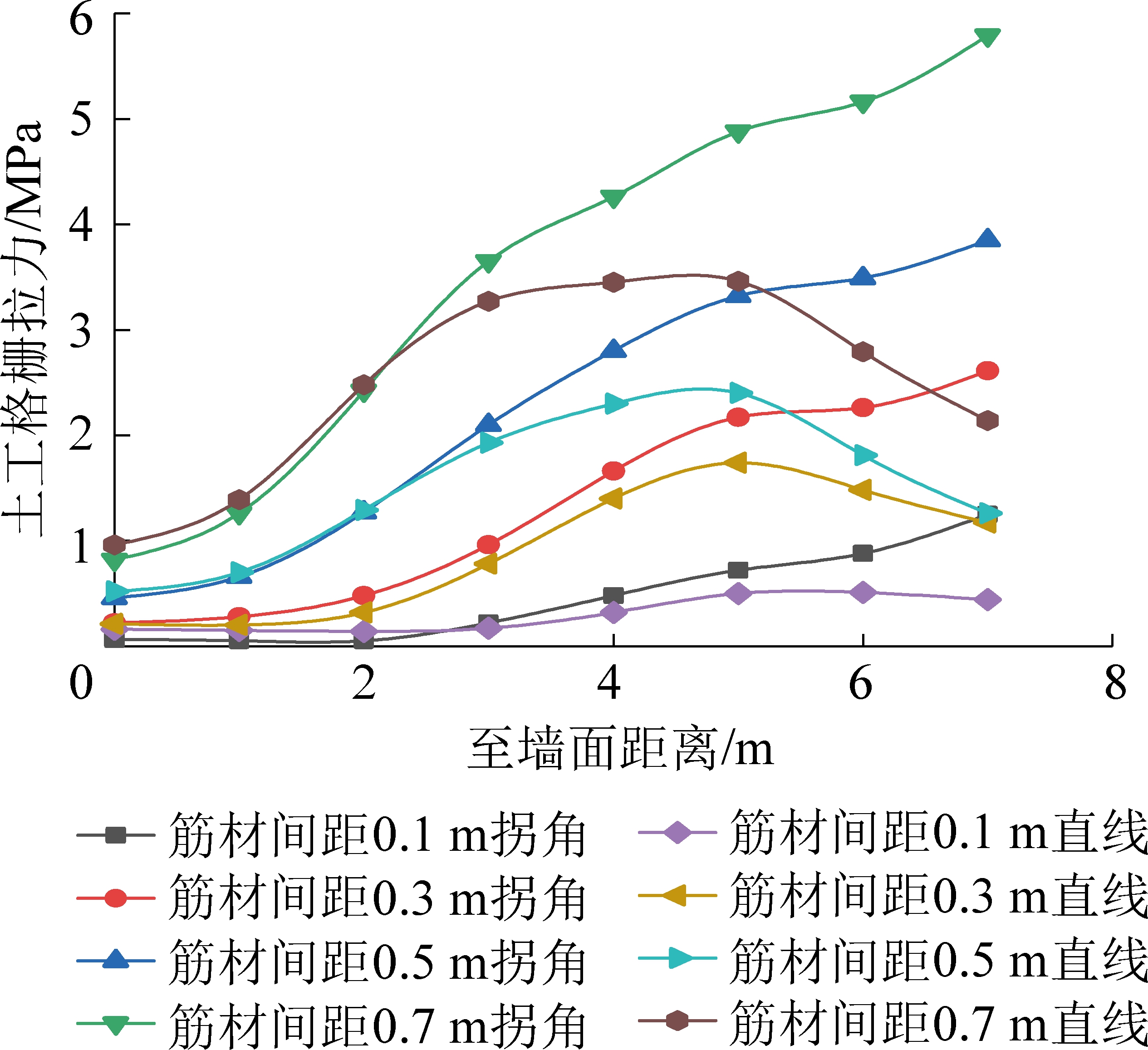
图7 拐角和直线部位顶层格栅拉应力分布曲线(剖面)
Fig.7 Top geogrid tension stress distribution curve (sections of corners and straight part)
公路桥梁设计规范(2007年):筋材最小长度≥0.7倍挡墙高度,且≥2.4 m。
根据规范要求选取筋材长度分别为7、8、9、10和11 m,使用FLAC3D软件建立相应的加筋土挡墙拐角部位三维模型,加筋层间距为0.5 m,其余参数不变,研究加筋长度对加筋土挡墙顶层土工格栅拉应力的影响。
通过各筋材长度下土工格栅拉应力分布图8a和顶层土工格栅拉应力分布图8b(以筋材长度9 m为例)可以看出,拐角部位土工格栅拉应力分布规律与直线部位有明显区别。将各筋材长度的顶层土工格栅边线上的拉应力数据绘制成如图9所示:边线上土工格栅拉应力分布规律及大小不受加筋长度的影响。

图8 加筋长度9 m土工格栅拉应力分布
Fig.8 Geogrid tensile stress distribution of reinforcement length 9 m
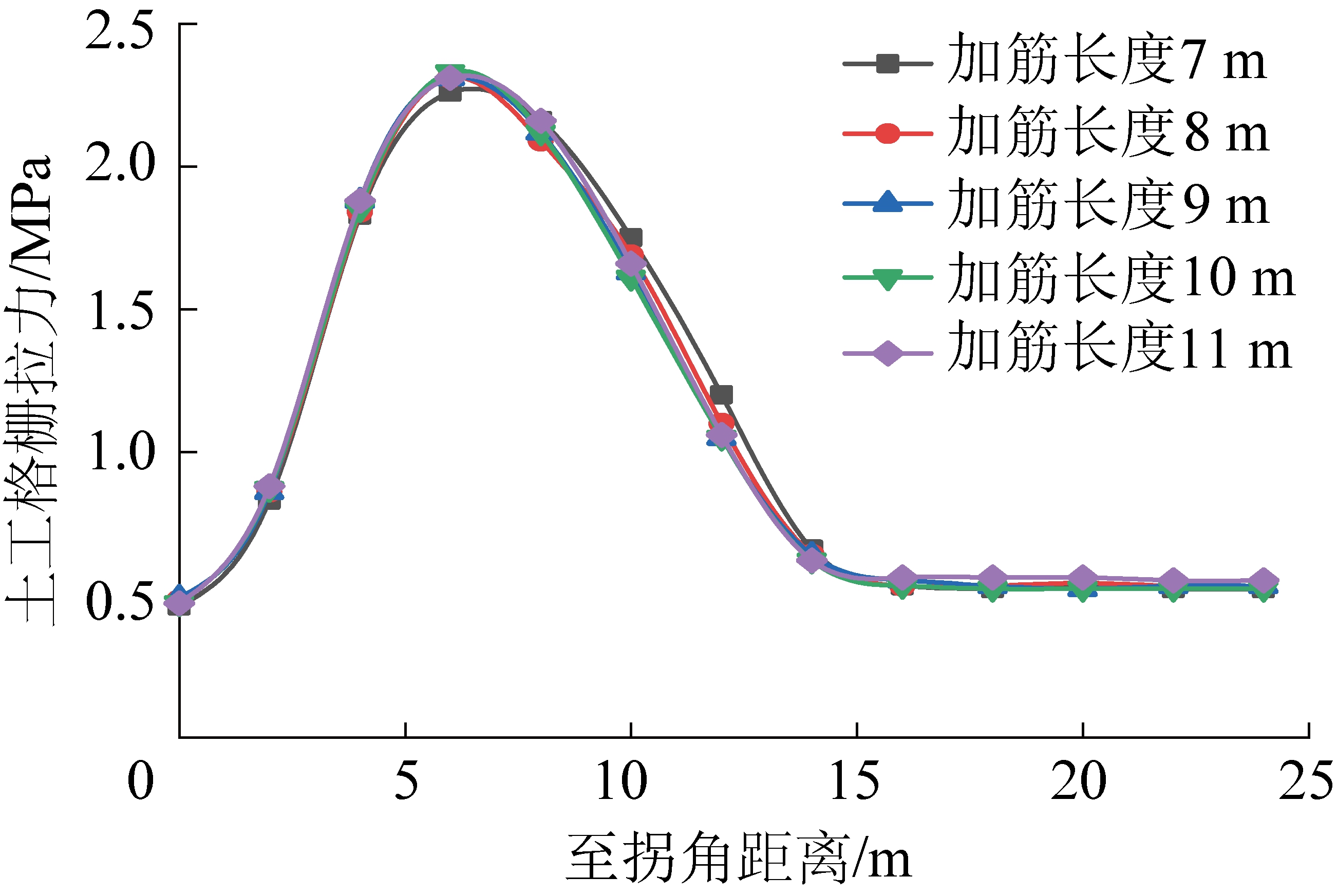
图9 土工格栅外缘拉应力分布(加筋长度)
Fig.9 Outer edge tensile stress distribution curve (reinforcement length)
图10为各加筋长度下拐角平分线顶层土工格栅的拉应力分布。距墙面7 m时土工格栅拉应力最大;距墙面7~9 m,随着加筋长度的增加,土工格栅拉应力先减小后增大,距墙面距离大于9 m时土工格栅拉力只减不增。
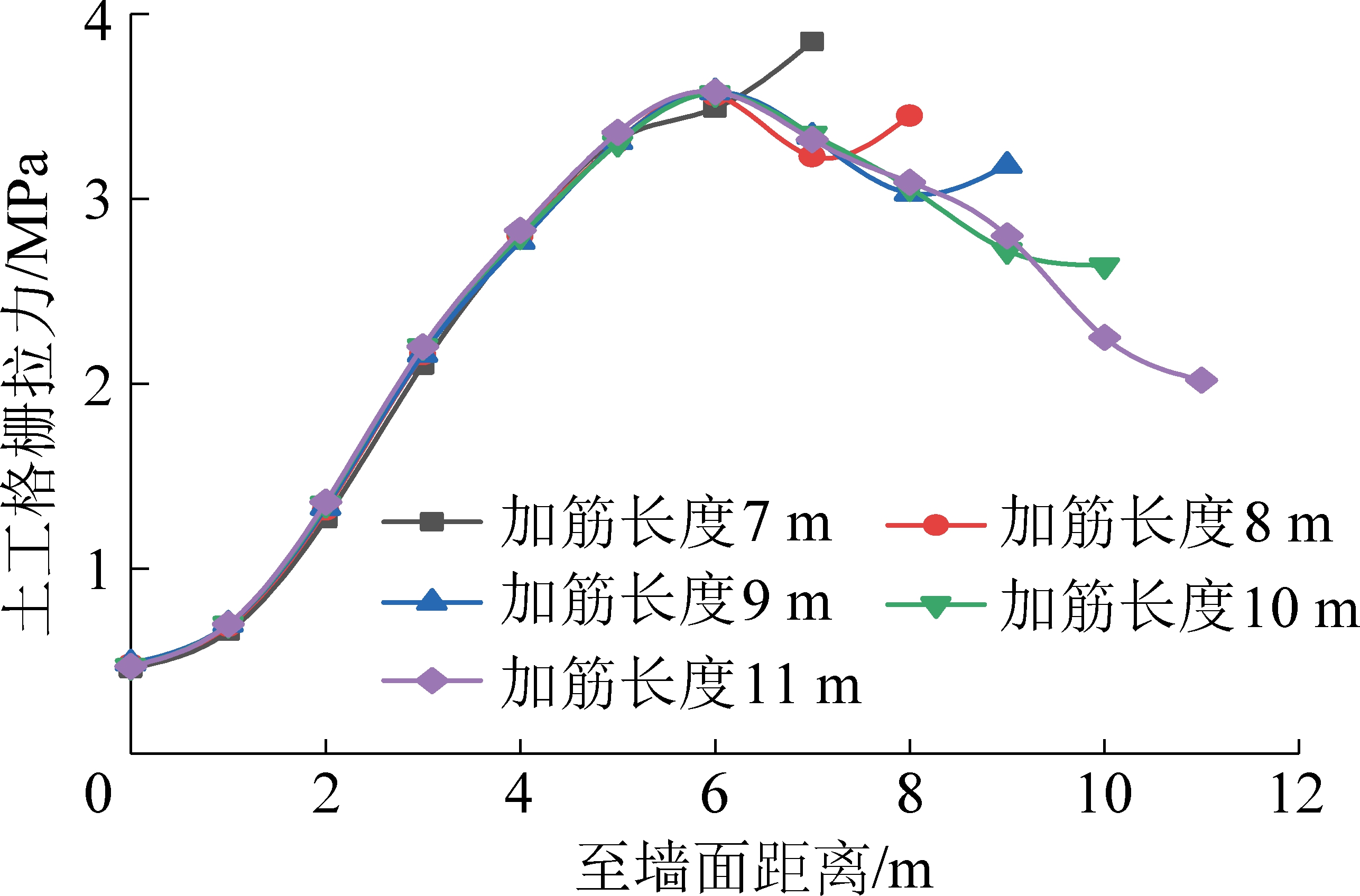
图10 拐角和直线部位顶层格栅拉应力分布曲线(剖面)
Fig.10 Top geogrid tension stress distribution curve (sections of corners and straight part)
综合边线上土工格栅拉应力的分布规律及拐角平分线上的土工格栅分布规律,考虑到经济的合理性及筋长的作用效果,筋材长度8~10 m最佳。
工程上在设计加筋土挡墙时,直接将两侧直线挡墙延伸到拐角部位衔接起来,常常把拐角部位的特殊结构忽略,导致设计不完善出现挡墙稳定性不足而发生病害。通过在拐角部位增设辅筋(加强筋)研究土工格栅拉应力变化特征来增强该部位稳定性。
研究采用3种辅筋布设方式如图11c所示,布设区域如图11a、11b所示:① 辅筋10 cm:与土工格栅间距10 cm处再布设一层筋材;② 辅筋20 cm:与土工格栅间距20 cm处再布设一层筋材;③ 一半辅筋:在挡墙上半部分或下半部分布设筋材,并且与土工格栅间距为20 cm,整个布设过程筋材参数保持不变。

图11 辅筋布设方式
Fig.11 Diagram of the way the auxiliary geogrids laying
图12和图13分别为整体辅筋(以辅筋间距20 cm为例)和一半辅筋(以墙高上半部分辅筋为例)的土工格栅拉应力分布图和顶层土工格栅拉应力分布图。整体辅筋时,墙高中下部拐角部位不再是土工格栅拉力最大处,拐角两侧沿墙面延伸大于拐角部位。将辅筋方式分别为无辅筋、辅筋长度10 cm、辅筋长度20 cm、一半辅筋的顶层土工格栅边线上的拉应力数据绘制成图14所示。边线上的土工格栅拉应力受辅筋方式的影响较大,相较于整体增设辅筋,一半辅筋对挡墙拐角处土工格栅变形的控制效果较弱,但可以起到很好的控制作用,也能节约材料,具体运用中根据实际情况拟定方案;在墙高上半部分增设辅筋对拐角部位的变形控制效果优于在墙高下半部分增设辅筋;辅筋与土工格栅之间的间距大小对土工格栅的拉应力影响较小,工程上可根据实际需求进行合理选择(相关技术规范:间距不宜小于5 cm[24])。随着距拐角距离(0~15 m)的增大土工格栅拉应力出现先增后减的变化规律,且在6 m处最大,15 m后变化较小,这与直线型加筋土挡墙规律相同。
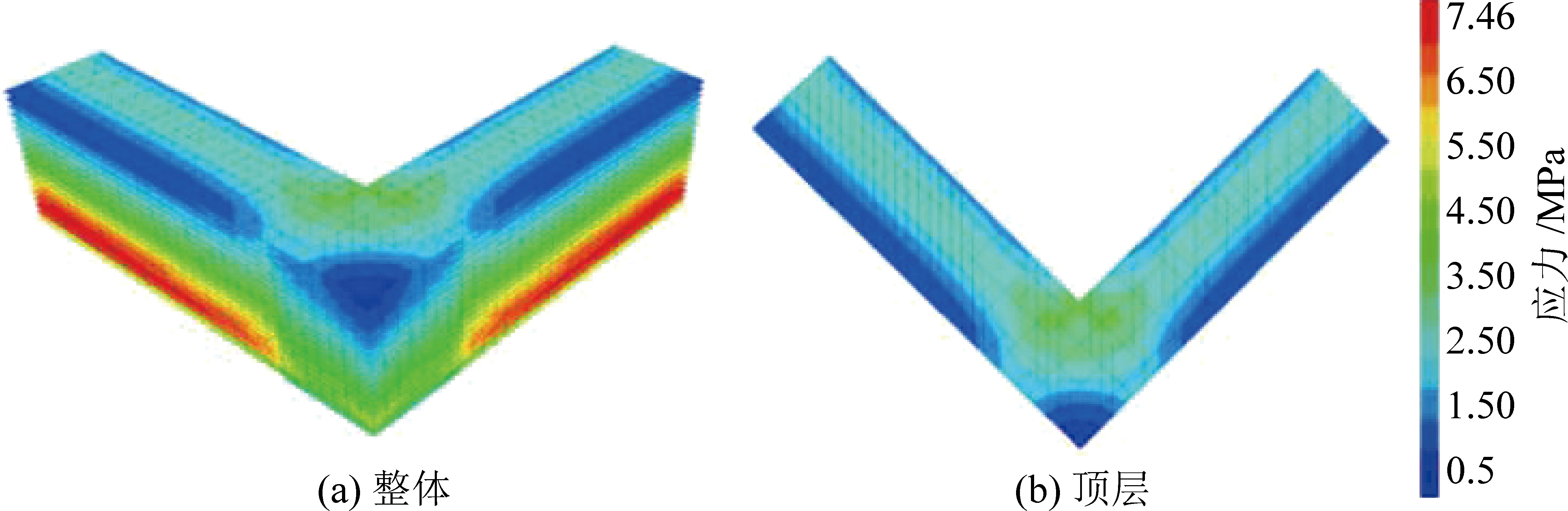
图12 土工格栅拉应力分布(辅筋20 cm)
Fig.12 Tensile stress distribution diagram of geogrid under 20 cm spacing of auxiliary reinforcement
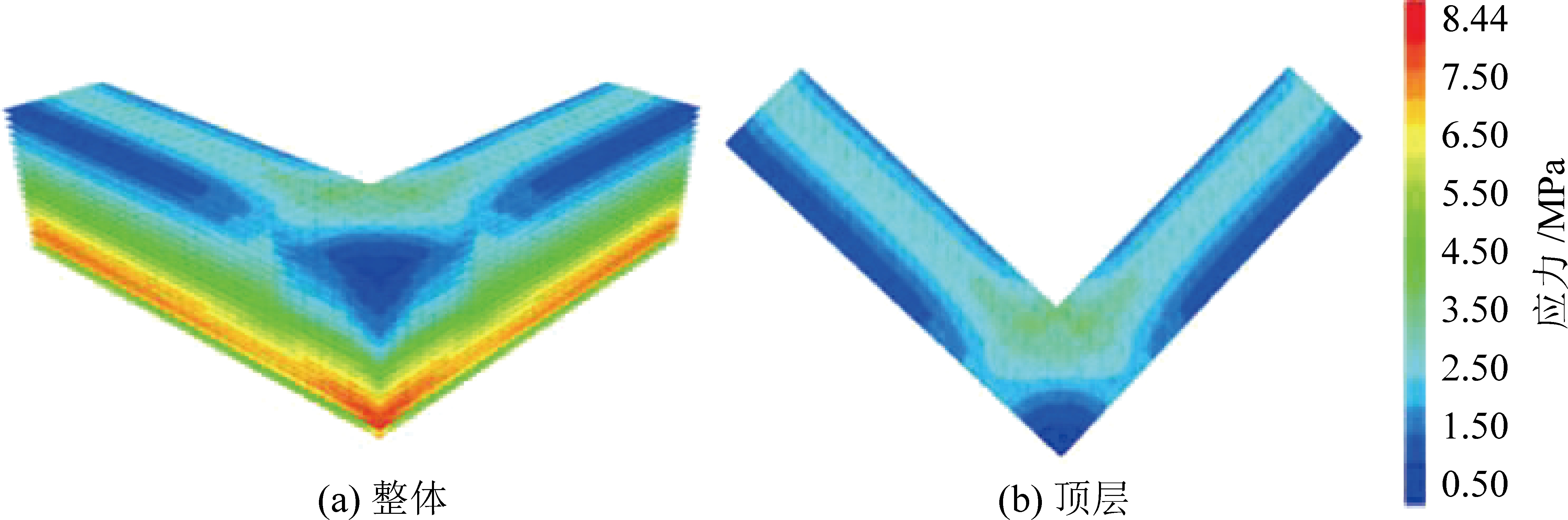
图13 土工格栅拉应力分布(墙高上半部分辅筋)
Fig.13 Tensile stress distribution diagram of geogrid for auxiliary reinforcement in the upper half of wall
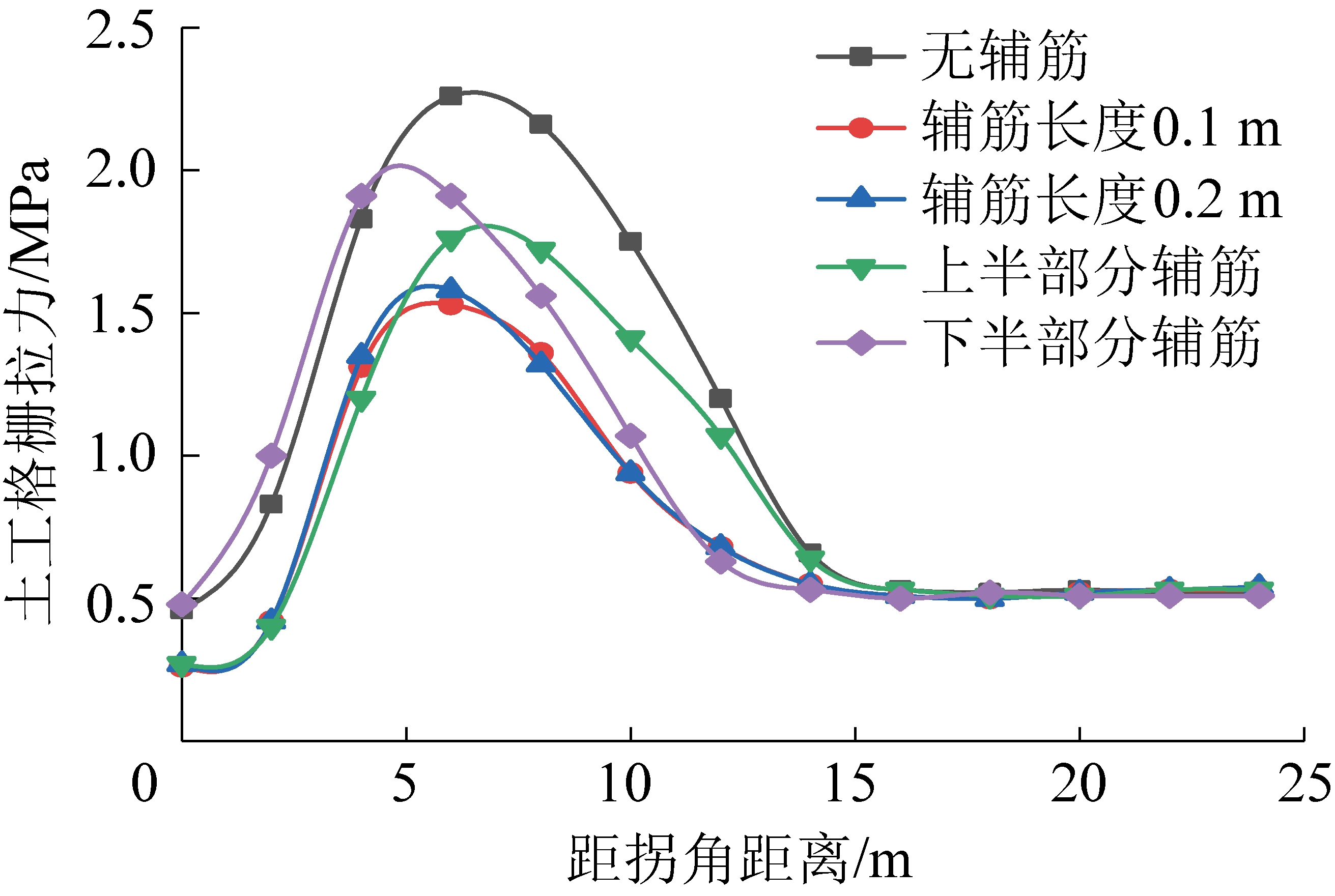
图14 土工格栅外缘拉应力分布(辅筋)
Fig.14 Outer edge tensile stress distribution curve(auxiliary reinforcement)
图15为辅筋布设方式分别为无辅筋、辅筋10 cm、辅筋20 cm和一半辅筋下顶层土工格栅在拐角平分线上的最大拉应力分布。可知:布设辅筋对拐角平分线上的土工格栅拉应力有明显影响;土工格栅拉应力基本不受辅筋间距大小的影响;随着距墙面距离的增大土工格栅最大拉应力呈线性增长趋势;距墙面1~6 m时整体布设辅筋土工格栅拉应力比墙高上半部分布设辅筋小,即相应的破坏范围较小,墙高下半部分布设辅筋比无辅筋时土工格栅拉应力都大,即考虑一半辅筋时可在墙高上半部分增设辅筋。
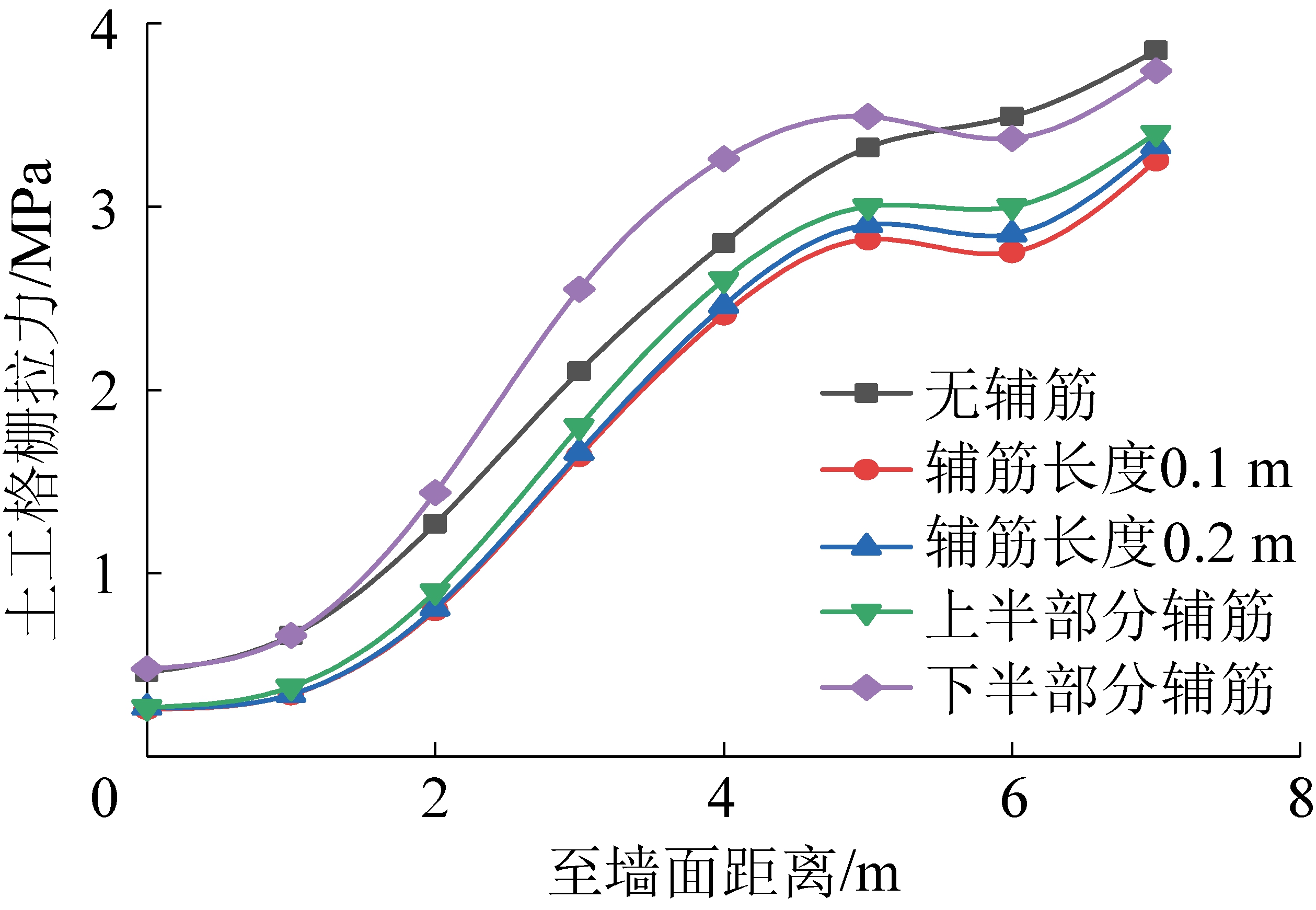
图15 拐角和直线部位顶层格栅拉应力分布(剖面)
Fig.15 Top geogrid tension stress distribution curve (sections of corners and straight part)
吴迪等[25]通过物理模型试验研究各层筋带拉力变化如图16所示,在相同间距下,各层筋带拉力值按距离面板的距离,呈先增大后减小趋势;在不同加筋间距下,土体未发生破坏前,各层筋带的拉力,随加筋间距增大而有所增大。将本次筋材间距影响下的直线部位数值模拟结果与已有的试验结果进行了比较。数值模拟与试验结果2种方法得到的筋带拉力变化规律高度吻合。进而说明本次数值模型的正确性及合理性,即通过本次数值模型研究拐角部位土工格栅拉应力具有合理性。
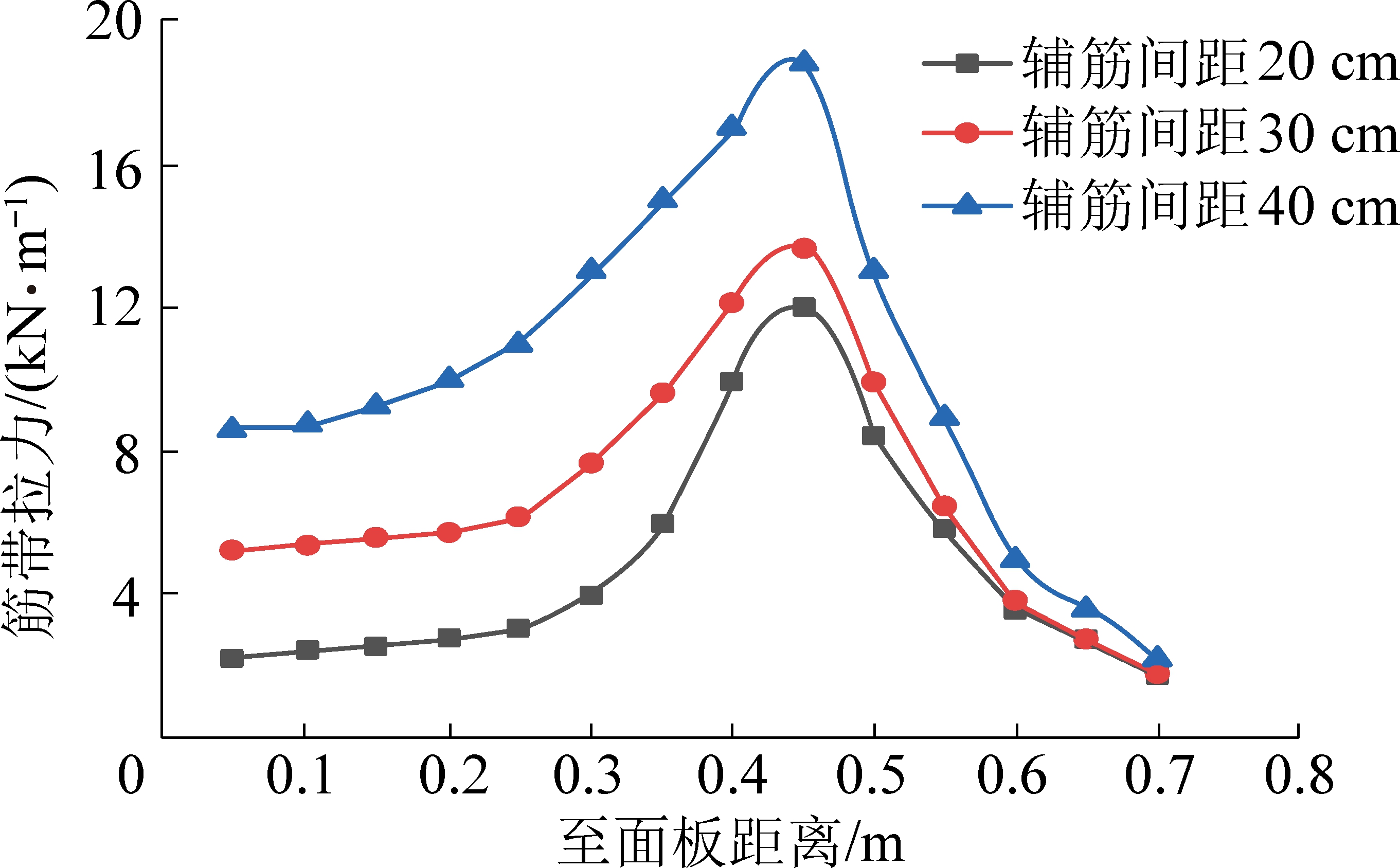
图16 不同加筋间距下筋带拉力对比
Fig.16 Comparison of tensile stress under different reinforcement spacing
分析研究了拐角部位顶层土工格栅拉应力变形规律在各因素下的影响,为使设计的加筋土挡墙更科学、更安全,将各个因素对拐角部位顶层土工格栅拉应力影响的变形规律进行对比。
图17是3种影响因素下土工格栅外缘拉应力分布曲线图。可知,加筋间距对土工格栅拉应力影响最大,辅筋方式次之,加筋长度基本没有影响,可忽略不计;相较于整体增设辅筋,一半辅筋对挡墙拐角处土工格栅变形的控制效果较弱,但可以起到很好的控制作用,具体运用中为节约材料,根据实际情况可以选择一半辅筋方式,即在墙高上半部分辅筋。
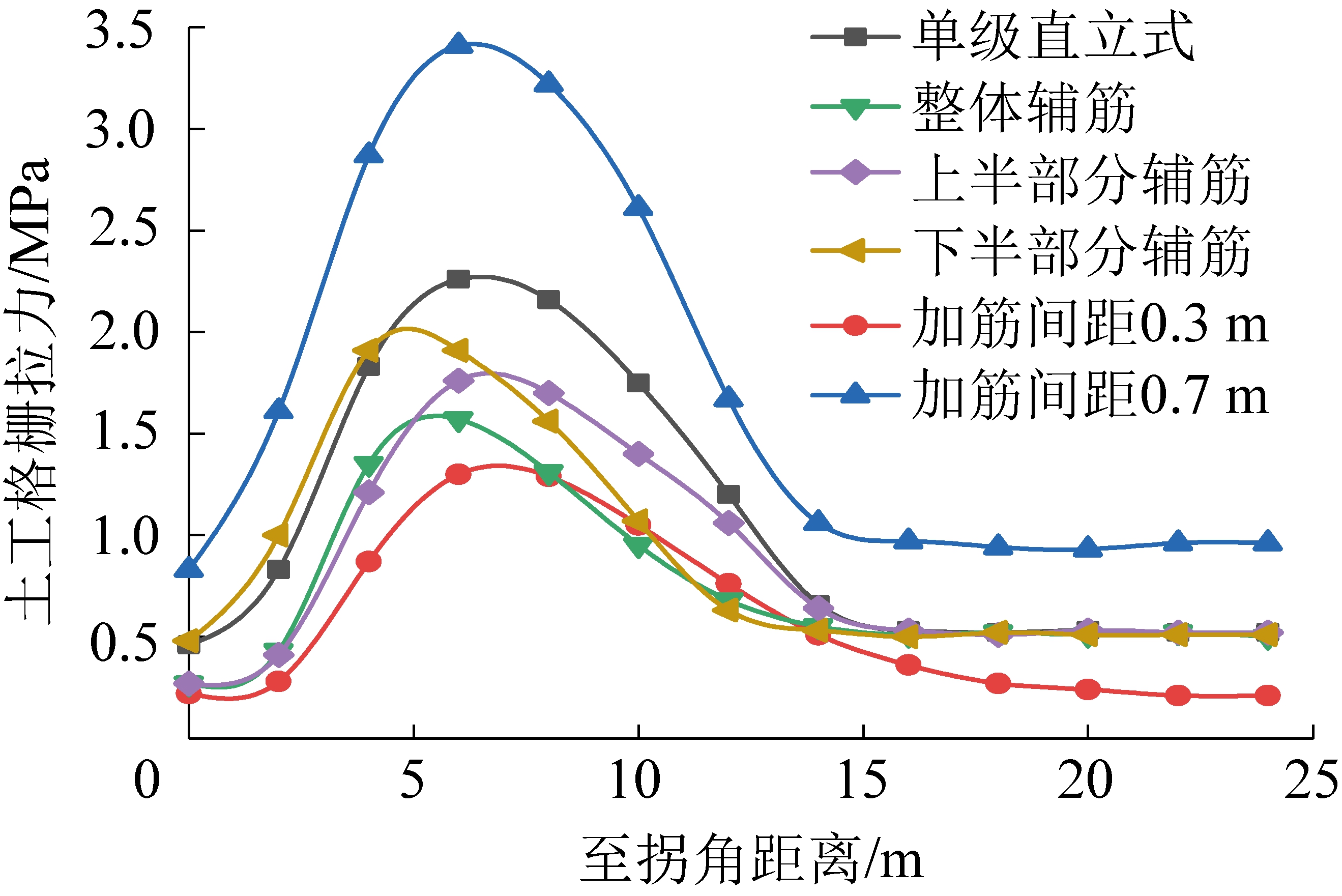
图17 3种影响因素下土工格栅外缘拉应力分布
Fig.17 Distribution curve of tensile stress at the outer edge of geogrid under three influencing factors
图18为3种影响因素下拐角平分线顶层格栅拉应力分布曲线图。筋材间距对土工格栅拐角平分线上拉应力影响较大,辅筋方式次之,加筋长度最小;为减小拐角平分线上土工格栅破坏程度,优先考虑改变筋材间距大小;在墙高下半部分辅筋没有起到加筋效果,故为减少资源浪费,可在墙高上半部分进行辅筋。综合比较各因素对拐角平分线上格栅拉力的影响程度及工程施工更加经济合理,可选择改变筋材间距大小及在墙高上半部分辅筋来减小拐角平分线上土工格栅破坏程度。
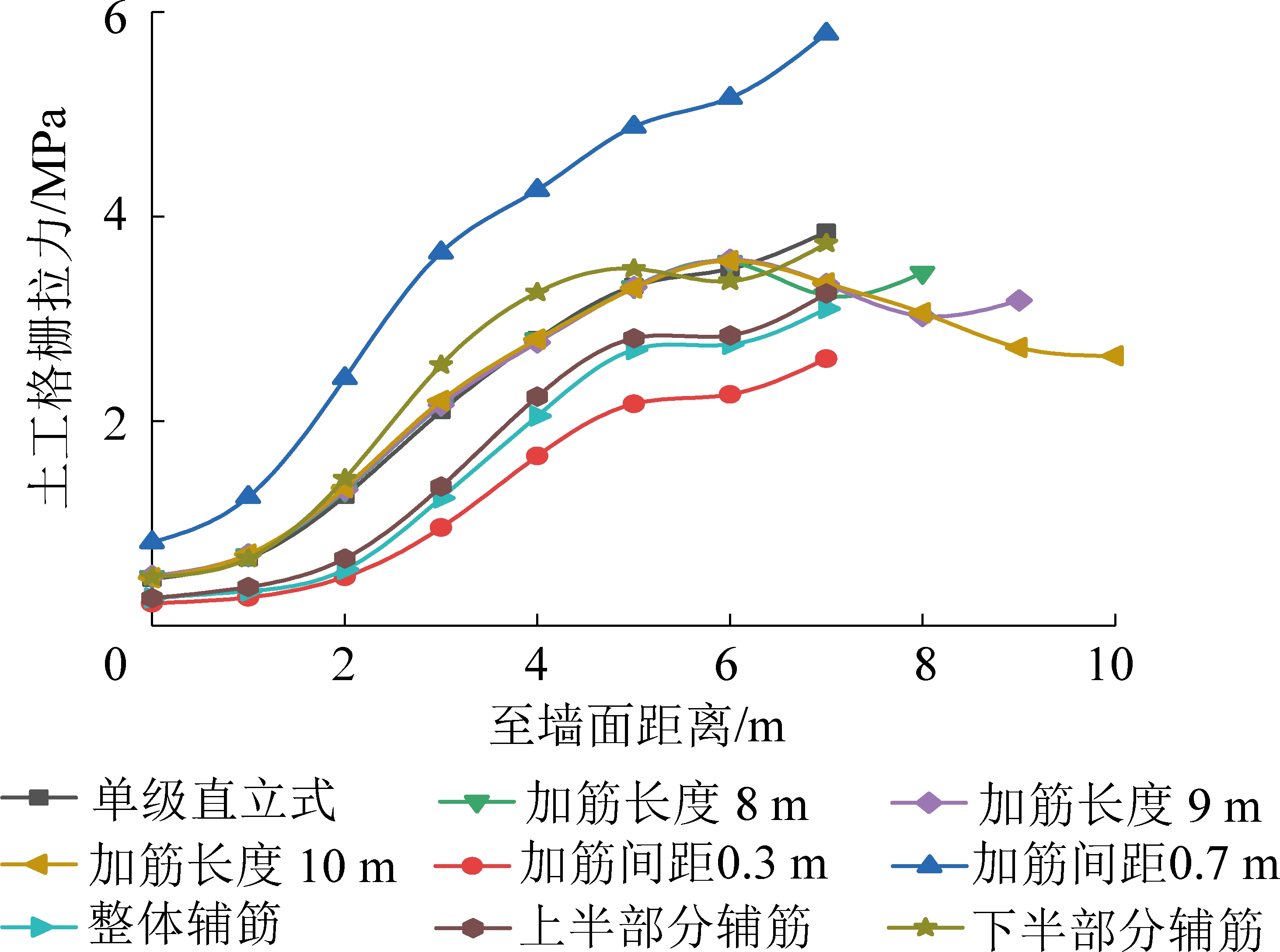
图18 3种影响因素下拐角平分线顶层格栅拉应力分布曲线
Fig.18 Distribution curve of tensile stress of top geogrid under three influencing factors(corner)
由3种因素对加筋土挡墙顶层土工格栅变形规律影响的对比分析,旨在设计更科学更安全的加筋土挡墙,提出如下建议:
1)改变筋材间距大小对减小不规则状挡墙土工格栅破坏程度效果最好,在经济条件允许的情况下,可选择筋材间距大小为0.3 m。
2)增设辅筋不如改变筋材间距大小效果好,但这种方法节约材料,可以选择整体辅筋及一半辅筋的方式,工程上为节省材料可选择一半辅筋方式,即在墙高上半部分辅筋。
3)筋材长度虽然影响不大,但在经济条件允许情况下,可选择筋材长度8~10 m效果最好。
1)由于特殊的墙体形态和受力状态,拐角部位呈现与直线部位明显的区别,并且变形量显著大于直线部位。
2)拐角部位和直线部位顶层土工格栅的拉应力分布规律有明显区别:拐角部位呈现“X”形,而直线部位与墙面平行分布。
3)筋材间距、辅筋方式都对加筋土挡墙拐角处土工格栅的变形有明显的影响,加筋长度基本没有影响。
4)土工格栅拉应力随着距拐角距离(0~15 m)的增大出现先增后减趋势,且在6 m处最大,15 m后变化较小,即实际工程中可在距拐角6 m左右提高挡土墙设计的稳定性。
5)对于减小顶层土工格栅的破坏程度,可通过改变筋材间距大小、增设辅筋的方式或这两种方法的结合来减小土工格栅的破坏程度;辅筋与主筋的间距大小对土工格栅的影响较小,但一般要求其间距不小于5 cm。
[1] WU J T H,LEE K Z.Pham Allowable bearing pressures of bridge sills on GRS abutments with flexible facing[J].Journal of Geotechnical and Geoenvironmental Engineering,2006,132(7):830-841.
[2] 张孟喜,黄 超.刚性条带式带齿加筋土的极限拉拔力模型[J].岩土工程学报,2009,31(9):1336-1345.
ZHANG Mengxi,HUANG Chao.Ultimate pullout resistance model for rigid denti-strip reinforced soil [J].Chinese Journal of Geotechnical Engineering,2009,31(9):1336-1345.
[3] 李鸿强,龙建辉,任俊姣,等.不同拐角形式的加筋土挡墙变形特征分析[J].煤炭科学技术,2021,49(11):118-124.
LI Hongqiang,LONG Jianhui,REN Junjiao,et al.Analysis of deformation characteristics of reinforced earth retaining walls with different corners[J].Coal Science and Technology,2021,49(11):118-124.
[4] YAZDANDOUST,MAJID.Laboratory evaluation of dynamic behavior of steel-strip mechanically stabilized earth walls[J].Soils and Foundations,2018,58(2):264-276.
[5] 田迎斌,李学良.采动区钢筋混凝土灌注桩受力特性分析及抗变形技术[J].煤炭科学技术,2020,48(10):173-178.
TIAN Yingbin,LI Xueliang.Analysis of mechanical characteristics and anti-deformation design of reinforced concrete cast-in-place pile in mining process[J].Coal Science and Technology,2020,48(10):173-178.
[6] 中华人民共和国交通部.公路加筋土工程设计规范:JTJ015-91[S].北京:人民交通出版社,1999.
[7] 中华人民共和国铁道部.铁路路基支挡结构设计规范:TB10025-2006[S].北京:中国铁道出版社,2006.
[8] 刘晓明,袁振宇,陈昌富,等.红砂岩地区某加筋土挡土墙凸形拐角鼓胀病害分析[J].土木工程学报,2011(S2):18-22.
LIU Xiaoming,YUAN Zhenyu,CHEN Changfu,et al.Analysis of convex swelling of a reinforced earth retaining wall in red sandstone area[J].China Civil Engineering Journal,2011(S2):18-22.
[9] KI,JUNG SU,REW,et al. A behavior of curve section of reinforced retaining wall by model test[J].Journal of The Korean Society of Civil Engineers,2012,32(6C):249-257.
[10] ZHANG F,LESHCHINSKY D,GAO Y F,et al.Three-dimensional slope stability analysis of convex turning corners [J].Geotech.Geoenviron.Eng.,2018,144(6):06018003-1-06018003-7.
[11] ZHANG F,GAO Y F,LESHCHINSKY D,et al.3D effects of turning corner on stability of geosynthetic-reinforced soil structures[J].Geotextiles and Geomembranes,2018,46(4):367-376.
[12] ZHANG F,LESHCHINSKY D,GAO Y F,et al.Corner reinforced slopes:Required strength and length of reinforcement based on internal stability[J].Geotextiles and Geomembranes,2019,47:408-416.
[13] KOERNER R M,SOONG T Y.Geosynthetic reinforced segmental retaining walls[J].Geotextiles &Geomembranes,2001,19(6):359-386.
[14] 刘华北,LING H I.土工格栅加筋土挡土墙设计参数的弹塑性有限元研究[J].岩土工程学报,2004,26(5):668-673.
LIU Huabei,LING H I.Elasto-plastic finite element study for parameters of geogrid-reinforced soil retaining wall[J].Journal of Geotechnical Engineering,2004,26(5):668-673.
[15] 叶观宝,张 振,邢皓枫,等.面板对路堤式加筋土挡墙力学特性的影响[J].岩土力学,2012,33(3):881-886.
YE Guanbao,ZHANG Zhen,XING Haofeng,et al.Influence of facing on mechanical behavior of reinforced retaining wall for embankment[J].Rock and Soil Mechanics,2012,33(3):881-886.
[16] 徐 鹏,蒋关鲁,王 宁,等.填土相对密实度对加筋土挡墙的影响研究[J].岩土力学,2018,39(11):102-108.
XU Peng,JIANG Guanlu,WANG Ning,et al.Centrifugal model test on influence of relative compactness on reinforced soil retaining walls[J].Rock and Soil Mechanics,2018,39(11):102-108.
[17] 杨广庆,徐 超,张孟喜.土工合成材料加筋土结构应用技术指南[M].北京:人民交通出版社,2016.
[18] 栾茂田,李敬峰,肖成志,等.土工格栅加筋挡土墙工作性能的非线性有限元数值分析[J].岩石力学与工程学报,2005,24(14):2428-2433.
LUAN Maotian,LI Jingfeng,XIAO Chengzhi,et al.Numerical analysis of performance of geogrids reinforced retaining walls by nonlinear FEM[J].Chinese Journal of Rock Mechanics and Engineering,2005,24(14):2428-2433.
[19] LESHCHINSKY D,VULOVA C.Numerical investigation of the effects of geosynthetic spacing on failure mechanism in MSE block walls [J].Geosynthetic International,2001,8(4):343-365.
[20] 杨广庆,周敏娟,张保俭.加筋土挡土墙水平位移研究[J].岩石力学与工程学报,2005,24(7):1248-1252.
YANG Guangqing,ZHOU Minjuan,ZHANG Baojian.Study on the horizontal deformation of reinforced retaining walls of soils[J].Journal of Rock Mechanics and Engineering,2005,24(7):1248-1252.
[21] 肖成志,栾茂田,杨 庆,等.加筋挡土墙长期工作性能的黏弹塑性有限元分析[J].岩石力学与工程学报,2006,25(10):1990-1996.
XIAO Chengzhi,LUAN Maotian,YANG Qing,et al.Numerical analysis of long-term performance of reinforced earth retaining walls by fem based on viscoelasto-plasticity [J].Journal of Rock Mechanics and Engineering,2006,25(10):1990-1996.
[22] 杨广庆,吕 鹏,张保俭,等.整体面板式土工格栅加筋土挡墙现场试验研究[J].岩石力学与工程学报,2007,26(10):2077-2083.
YANG Guangqing,LYU Peng,ZHANG Baojian,et al.Research on geogrids reinforced soil retaining wall with concrete rigid face by field test[J].Journal of Rock Mechanics and Engineering,2007,26(10):2077-2083.
[23] 龙建辉,焦 姗,王晓娅.考虑摩擦损耗的加筋挡土墙临界高度研究[J].土木工程学报,2018,51(1):124-128.
LONG Jianhui,JIAO Shan,WANG Xiaoya.Critical height research of reinforced retaining wall considering the friction loss[J].Journal of Civil Engineering,2018,51(1):124-128.
[24] 中华人民共和国铁道部.铁路路基土工合成材料应用技术规范:TB10118-2006[S].北京:中国铁道出版社,2006.
[25] 吴 迪,浦壮壮,李 丹,等.不同加筋间距对加筋土挡墙性能的影响研究[J].工程技术研究,2017(12):1-4.
WU Di,PU Zhuangzhuang,LI Dan,et al.Study on the influence of different reinforcement spacing on the performance of reinforced earth retaining wall[J].Engineering Technology Research,2017(12):1-4.