

锚杆钻机是现代化矿井巷道支护过程中高效、安全的自动化设备,极大地缓解了掘锚失调的问题。据统计我国国有重点煤矿掘进进尺5 000 km,锚杆支护比重占21%,相较发达国家,我国锚杆支护导致冒顶事故多,主要原因是现有支护作业中依然需要靠人工来完成拆、装钻杆/锚杆,紧固锚杆等工序动作,故存在很大的危险。国家煤矿安全监察局2019年发布的《煤矿机器人重点研发目录》[1-3]要求大力研发采煤、掘进、运输、安控、救援等应用煤矿机器人。《关于加快煤矿智能化发展的指导意见》明确指出研制钻锚支护机器人是解决巷道掘支速度慢、劳动强度大等的关键问题的有效途径。
在煤矿智能化核心技术[4-5]和巷道支护理论[6-9]的指导下,利用钻锚机械臂替代传统人工完成钻架的空间定位是井下自动支护作业[10-11]的关键。其中机械臂的控制效果直接影响着自动钻架的定位准确性和快速性。目前,机械臂通常采用电-液比例控制系统实现井下空间定位,不仅成本低且具有较好的控制效果。为进一步提高定位精度和速度,众多学者和相关科研人员开展了钻锚机械臂的独立关节控制方法及效果的研究。
比例积分微分控制PID的控制原理简单、鲁棒性和实用性强[12-14],在煤矿机械控制系统中得到了广泛应用,但随着现在的巷道的掘进速度和采煤量的提高,从而对钻锚机械臂的操作方式、工序时间及安全性均提出了新的要求,尤其是在环境恶劣、空间受限的工况下,机械臂末端在承受钻架自重和约20 000 N打钻力的影响下依旧能够在顶板准确找到直径为22 mm的孔位置,同时有效避开网格钢筋,保证钻锚工作时间不超过3 min。针对上述工况,机械臂末端钻架孔的实时位姿和定位精度就面临着非常大的控制技术挑战。应用传统PID控制效果并不理想,即使对PID参数重新设定依然达不到预期的控制目标,无法从本质上克服整数阶PID控制技术上的缺陷,很难实现机械臂精准的空间定位和轨迹规划。受限于传统参数整定方法依赖经验,很难在短时间内找到控制效果最好的一组参数,导致机械臂末端不能及时定位。
随着人工智能技术逐步发展和在工业领域的广泛应用,涌现出大量高效的优化算法,如遗传算法(GA)[15-17]、粒子群算法(PSO)[18-20]、搜索算法(GPS)[21]和鲸鱼算法(WOA)[22]等。将智能优化算法应用于PID控制器参数整定,可以大大改善PID的控制效果。鲸鱼算法属于元启发式优化算法,具有鲁棒性强、结构简单且控制参数少的特点,多数学者[23-25]应用鲸鱼算法在连续域问题优化领域取得了成功范例。
综上所述,相关专家对智能控制PID调参的方法进行了深入的研究并取得了大量成果,但是针对钻锚机械臂在井下完成自动支护作业的控制方法还需要进一步研究。主要由于钻锚机械臂在井下工作具有一些特殊性:①空间受限,环境复杂;②钻锚机械臂的末端主要与自动钻架连接,由于末端自重和打钻力约为20 000 N,会导致臂端振动较大,导致难以实现精准控制;③井下电气件都需要进行防止爆处理,尤其是传感器,相比较地面上的传感器很多性能指标难以达到,所以会影响钻锚机械臂在巷道空间中的精准定位。这严重制约了智能控制技术在井下煤矿机器人的应用。
从如何实现机械臂快速空间定位和轨迹跟踪的目标考虑,对钻锚机械臂的智能控制技术展开研究。根据旋量理论利用D-H法建立机械臂关节坐标系及坐标变换矩阵表达式,采用蒙特卡洛算法求解机械臂工作空间点云图。基于独立关节控制理论利用Matlab -Simulink软件,并结合分数阶FOPID控制技术,设计机械臂关节处液压马达/油缸单输入-单输出系统模型。分析基于遗传算法(GA)、粒子群算法(PSO)、鲸鱼算法(WOA),搜索算法(GPS)4种智能优化算法,从标准方差、超调量、稳定时间3个动态指标进行对比,分析液压马达/油缸的不同控制组合策略下阶跃影响的效果。通过仿真结果证明智能优化算法在改善控制精度方面具有明显效果,并进一步证实了组合控制策略在电液驱动控制系统中的有效性和实时性、准确性和快速性。为机械臂智能控制方法在井下应用奠定了理论基础。
钻锚机器人可以通过双目立体视觉实现机械臂孔位精确识别与定位,进而实现对煤矿巷道顶部、侧壁的全自动支护。机械臂是钻锚机器人的主要工作部件,一般由连杆、旋转减速器、联轴器、自动钻架等组成,机械臂的控制效果是保证钻锚机器人达到工作要求的重要因素之一。针对矿井巷道内环境恶劣、振动频繁、载荷多变的工况,为达到机械臂位移偏移量不得大于5 mm的具体要求,利用D-H法建立机械臂关节坐标系及坐标变换矩阵表达式,如图1所示。利用蒙特卡洛算法求解机械臂工作空间点云图,工作范围就要求钻锚机械臂的空间运动必须具有较高的控制精度,防止机械臂由于实时控制精度差或者控制不及时,导致机械臂与煤壁、机械臂与周围其他设备或者人员发生碰撞事故,影响人员安全和设备正常自动支护作业。

图1 D-H法机械臂各关节坐标系图
Fig.1 The coordinate system of each joint of the D-H method manipulator
分数阶控制作为控制领域的一个分支,具有参数调节灵活精密、系统稳定裕量大、系统鲁棒性强等诸多优点,现已广泛用于不同类型的控制器设计[26-28]。分数阶PIλDμ控制最早由Igor Podlubny提出,并通过响应分析论证了其相较于传统PID控制的优越性[29-32]。分数阶PIλDμ控制器的阶次参数λ、μ可以取任意实数,在P-I-D平面,可根据控制器参数的不同进行取值,FOPID控制系统结构如图2所示,其中r(t)为系统输入量,e(t)为偏差量,u(t)为输出量,y(t)为被控量。与传统PID控制相比,分数阶PIλDμ控制能更细微地体现比例控制到积分控制和微分控制的过渡过程,从而实现更精密、稳定性更好、抗干扰能力更强的控制效果[33-35]。
图2 FOPID控制系统结构
Fig.2 Structure of FOPID control system
FOPID控制器的数学表达式为:
(1)
式中:C(s)为R(s)作用下的传递函数;u(s)为控制器的输出;R(s)为控制器的误差输入;s为拉普拉斯算子;Kp为比例增益;Ki为积分增益;Kd为微分增益;λ,μ分别为分数阶微分、积分阶次。
基于分数阶PID控制算法的优势,提出基于WOA-FOPID算法的钻锚机械臂运动控制策略。其中关于FOPID的参数整定方法有很多种,根据算法本身的调节特点主要分为传统法整定和智能优化算法整定两类,而智能优化算法因为其自适应性被广泛使用[36-37]。将遗传算法、粒子群算法、搜索算法和鲸鱼算法4种智能优化算法分别与FOPID控制理论相结合,利用上述4种智能优化算法整定FOPID控制参数。智能控制算法FOPID控制系统结构如图3所示。

图3 智能控制算法FOPID控制系统结构
Fig.3 Structure of intelligent control algorithm FOPID control system
为充分探索遗传算法、粒子群算法、搜索算法和鲸鱼算法调参的优越性,将4种智能优化算法分别与PID、FOPID进行组合,通过不同的控制策略进一步分析机械臂的运动控制效果。智能优化算法整定FOPID参数的流程图如图4所示,根据控制系统特点和种群要求[38],参数设置如下:PSO参数设置为:Max_iter=200,N=20,C1=C2=1.49;GA参数设置为:N=50,Max_iter=200,变异参数为0.8,变异概率为0.75;WOA参数设置为:dim=5,Max_iter=50,SearchAgents_no=100;GPS参数设置为:dim=3,Max_iter=50,SearchAgents_no=100。
鲸鱼优化算法通过模拟座头鲸的捕食行为来搜索最优解[39-40],解决目标函数f(x)在D维的优化问题。参数整定及优化流程如图4所示。

图4 智能优化算法整定FOPID参数的流程
Fig.4 Flow of intelligent optimization algorithm for tuning FOPID parameters
Min f(x),s.t.1≤x≤u
(2)
1)初始化阶段。随机D维搜索空间中产生N个解,定义第i个解的位置xi(0)为:
xi(0)=[xi1(0),xi2(0),…,xiD(0)],i=1,…,N
(4)
由于最优设计在搜索速度中的位置不是先验已知的,因此假定当前最佳解是目标猎物或接近最优解。在定义了最佳搜索代理之后,其余搜索个体将依据最佳搜索代理更新位置。位置更新表达式为:
(5)
其中,D为搜索个体和最佳解之间的距离;x*(t)为当前最佳解的位置;A、C系数向量![]() 计算方式如下:
计算方式如下:
(6)
(7)
(8)
其中,在整个迭代过程中![]() 由2线性变化到
由2线性变化到![]() 和
和![]() 为[0,1]的随机数;tmax为最大迭代次数的设定值。
为[0,1]的随机数;tmax为最大迭代次数的设定值。
2)局部搜索阶段。通过收缩环绕和螺旋上升机制不断缩小包围圈并向上螺旋,模拟鲸鱼进行捕食,位置更新表达式为:
(9)
D′=|x*(t)-x(t)|
(10)
其中,![]() 为当前搜索个体与当前最优解向量;b为对数螺旋线形状的常数;l为随机数,范围是[-1,1];D′为当前搜索个体与当前最优解的距离;e为自然常数。
为当前搜索个体与当前最优解向量;b为对数螺旋线形状的常数;l为随机数,范围是[-1,1];D′为当前搜索个体与当前最优解的距离;e为自然常数。
当系数向量|A|<1时,意味着当前最新位置在收缩包围圈内游走,根据随机变量p来决定是否进行攻击还是包围目标,其数学模型为:
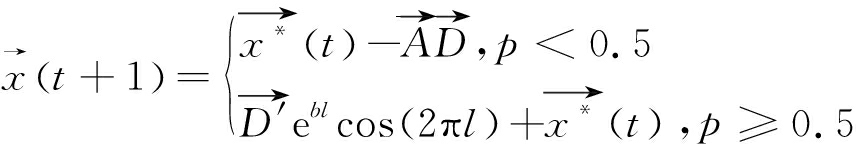
(11)
3)全局探索阶段。全局探索阶段是基于向量A的变化对猎物(探索)进行全局搜索。相对于局部搜索阶段,该阶段不再是依据当前最佳搜索个体为目标,而是根据随机选择的搜索个体来更新搜索个体在探索阶段的位置,其数学表达式为:
(12)
(13)
4)参数优化流程。运用WOA优化控制参数,优化变量表达为X=[x(1),x(2),x(3),x(4),x(5)],优化变量映射为鲸鱼的空间维度,dim=5,基于WOA优化FOPID控制参数优化流程如下:
Step1:算法初始化。设置控制参数目标函数的种群规模N、确定优化变量的空间维度dim、搜索的最大迭代次数Max-iter以及搜索目标数等相关参数。
Step2:分析比较每次搜索得到的优化变量所对应的目标函数值,进而确定最优个体的位置,定义为X*。
Step3:当p<0.5且|A|≥1时,根据式(12)来更新位置;当p<0.5且|A|<1时,根据式(5)来更新位置;当p>0.5且|A|<1时,根据式(9)来更新位置。
Step4:判断是否满足算法求解的误差精度以及终止条件,若满足,算法结束,输出最优变量及所对应目标函数值;否则,转到Step2,继续进行最优解的迭代。
1)WE9-62T-HR176-U液压马达数学建模及仿真测试。根据液压马达的相关参数,见表1。液压马达的整数阶数学模型[41-46]G(s)为
表1 液压马达的数学建模参数
Table 1 Mathematical modeling parameter of hydraulic motor

参数参数含义参数值Kα比例放大器的增益0.2 A/Vn阀芯的固有频率36m阀芯衔铁组件的质量0.5 kgξ阀芯的阻尼比16KS弹簧刚度5×103KI比例电磁铁的电压-力增益30 N/AKmi电压-电流增益5 V/AKxi阀芯电压-位移增益300Kc流量-压力系数2.8×10-12 m5/(N·s)Kq流量增益7.78×10-4 m2/sCtm液压马达总泄漏系数5.18×10-13 m5/(N·s)Kce比例阀总流量-压力系数3.32×10-12 m5/(N·s)Dm马达排量2.5×10-5 m3/radh马达固有频率11.7 rad/sξh马达阻尼比1.3βe有效体积弹性模量6.9×108 N/m2Vt液压马达和连通管道总容积3×10-4 m3Bm液压马达和负载的黏性阻尼系数4 500J液压马达和负载等效到马达轴上的总惯量42 kg·m2Cd电磁比例方向阀的流量系数0.6ρ液压油密度860 kg·m3

![]()
(14)
液压马达的分数阶数学模型[47-50]为

![]()
(15)
分数阶FOPID控制器表达式[51-53]:
Gc=0.487+5.404 2s-0.023+5.483 7s1.290 8
(16)
整数阶PID控制器表达式[53-55]:
Gc=30+1.695 2s-2+24.519 7s
(17)
在Matlab-Simulink软件中构建液压马达智能优化算法整定FOPID的控制系统的仿真模型,通过仿真分析可知,调节系统的各个组合策略动态响应曲线对比如图5—图8所示。图5为各智能算法与PID组合策略的阶跃响应,图6为各智能算法与FOPID组合策略的阶跃响应;图7为4种智能优化算法的PID和FOPID组合控制策略的对比,图8为WOA-FOPID和WOA-PID适应度函数数值迭代过程曲线。不同组合策略和控制指标对比见表2。
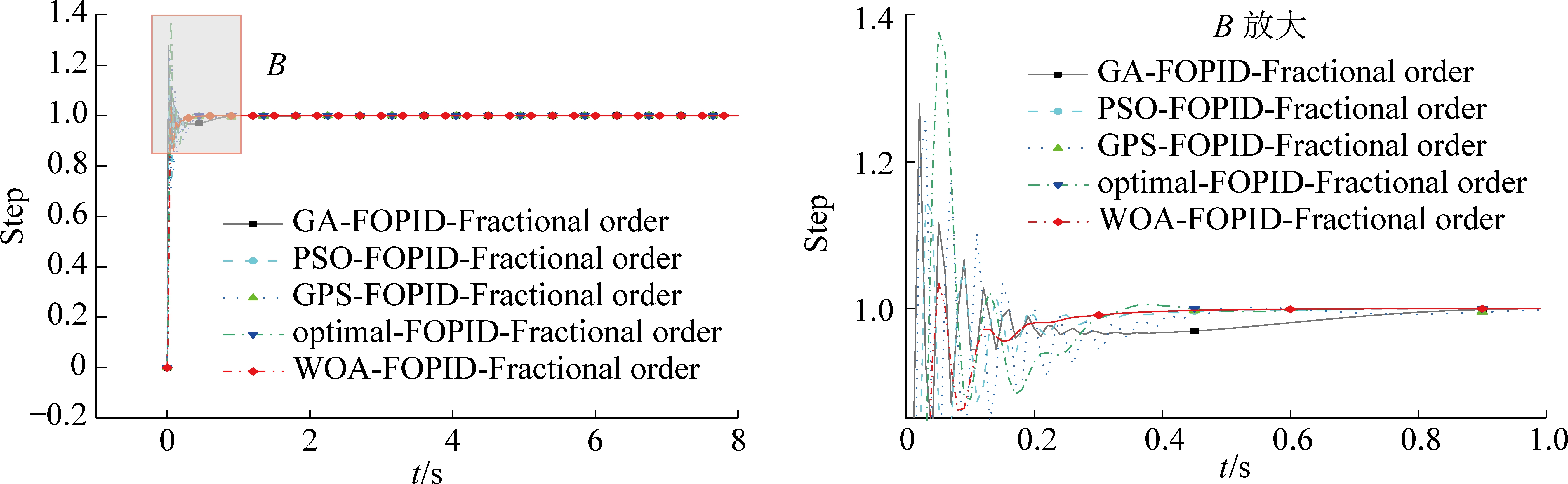
图6 各智能算法与FOPID组合策略的阶跃响应
Fig.6 Step response of each intelligent algorithm and FOPID combination strategy

图7 四种智能优化算法的PID和FOPID组合控制策略对比
Fig.7 Comparison of PID and FOPID combined control strategies of four intelligent optimization algorithms
仿真模型中分别采用4种智能控制算法对FOPID控制器-整数阶被控对象、FOPID控制器-分数阶被控对象、PID控制器-分整数阶被控对象及FOPID控制器-分整数阶被控对象进行参数整定。由图5—图8和表2可知,根据大量的仿真试验结果来看,在复杂系统中,相较于FOPID来说,PID控制并不占优势,超调量几乎都在30%左右,稳定时间在0.7 s左右浮动,数据结果显示,基于WOA算法进行参数整定的系统具有一定优势,稳定时间减少至0.3 s左右。
表2 不同组合控制策略和控制指标
Table 2 Different combination control strategies and control indicators

组合动态指标标准方差超调/%稳定时间/sGA-FOPID-Integer order0.058 6539.000.29PSO-FOPID-Integer order0.058 5338.720.28GPS-FOPID-Integer order0.044 4023.450.41Optimal-FOPID-Integer order0.058 6938.820.28WOA-FOPID-Integer order0.036 5315.180.09GA-FOPID-Fractional order0.039 4427.910.59PSO-FOPID-Fractional order0.047 5025.520.52GPS-FOPID-Fractional order0.045 4726.120.39Optimal-FOPID-Fractional order0.058 0337.670.28WOA-FOPID-FrActional order0.055 293.490.19GA-PID-Integer order0.044 2129.590.7PSO-PID-Integer order0.044 2129.600.7GPS-PID-Integer order0.044 2129.600.7Optimal-PID-Integer order0.070 3453.570.27WOA-PID-Integer order0.040 9227.030.34GA-PID-Fractional order0.044 8030.700.67PSO-PID-Fractional order0.044 8030.700.67GPS-PID-Fractional order0.044 8030.700.67Optimal-PID-Fractional order0.070 2753.300.27WOA-PID-Fractional order0.401 9026.270.31

图5 各智能算法与PID组合策略的阶跃响应(step)
Fig.5 Step response of each intelligent algorithm and PID combination strategy
整体来看,FOPID控制器对于分数阶被控对象有更好的控制效果,超调量有所降低。从数据结果来看,WOA算法的寻优能力明显,对于分数阶被控对象在0.19 s就可以达到稳定,且超调量为3.49%,说明被控系统具有更好的稳定性,充分体现了分数阶FOPID控制器的优越性。如图8所示,仿真结果表明分数阶WOA-FOPID控制器在响应速度、调节时间、稳态精度上,控制效果均优于分数阶GPS-FOPID控制器、整数阶GPS-PID控制器、分数阶GA-FOPID控制器、整数阶GA-PID控制器、分数阶PSO-FOPID控制器、整数阶PSO-PID控制器和整数阶WOA-FD控制器。

图8 WOA-FOPID和WOA-PID适应度函数数值迭代过程曲线
Fig.8 Curve of numerical iteration process of WOA-FOPID and WOA-PID fitness function
根据以上研究结论,直接将智能优化鲸鱼算法WOA直接应用到机械臂中油缸DOA090470-1(1)和DOA090260-1中系统控制器进行参数整定,并对不同组合的控制策略进行对比和分析。
2)DOA090470-1(1)液压油缸数学建模及仿真测试。根据液压马达的相关参数,见表3。DOA090470-1(1)液压缸的整数阶数学模型[57-58]:
表3 DOA090470-1(1) 液压油缸参数
Table 3 DOA090470-1(1) hydraulic cylinder parameter

序号符号参数含义参数值1Xp液压缸活塞位移—2h液压固有频率16.77 rad/s3M负载总质量—4ξh液压阻尼比0.615Bp负载的黏性阻尼系数—6kx电液比例阀的增益7.78×10-47Ki比例放大器的增益0.28Kq液压缸流量增益3009U电位信号—10Ap活塞有效面积9.6×10-4 m3

![]()
(18)
DOA090470-1(1)液压缸的分数阶数学模型[58]:

(19)
整数阶PID控制器表达式[51-53]:
Gc=18.402 2+30s-1
(20)
分数阶FOPID控制器表达式[54-56]:
Gc=3.066 9+29.980 5s-1.812+30s0.000 002
(21)
由图9和表4可知,PID控制器在复杂系统中不具有优势,结果显示不能微调,PID控制分数阶作用于被控对象时尤为明显,6.06 s时才逐渐趋于稳定;在复杂系统中FOPID控制器对于分数阶被控对象有更好的控制效果,超调量为8.672%,在0.02 s内就可以趋于稳定。
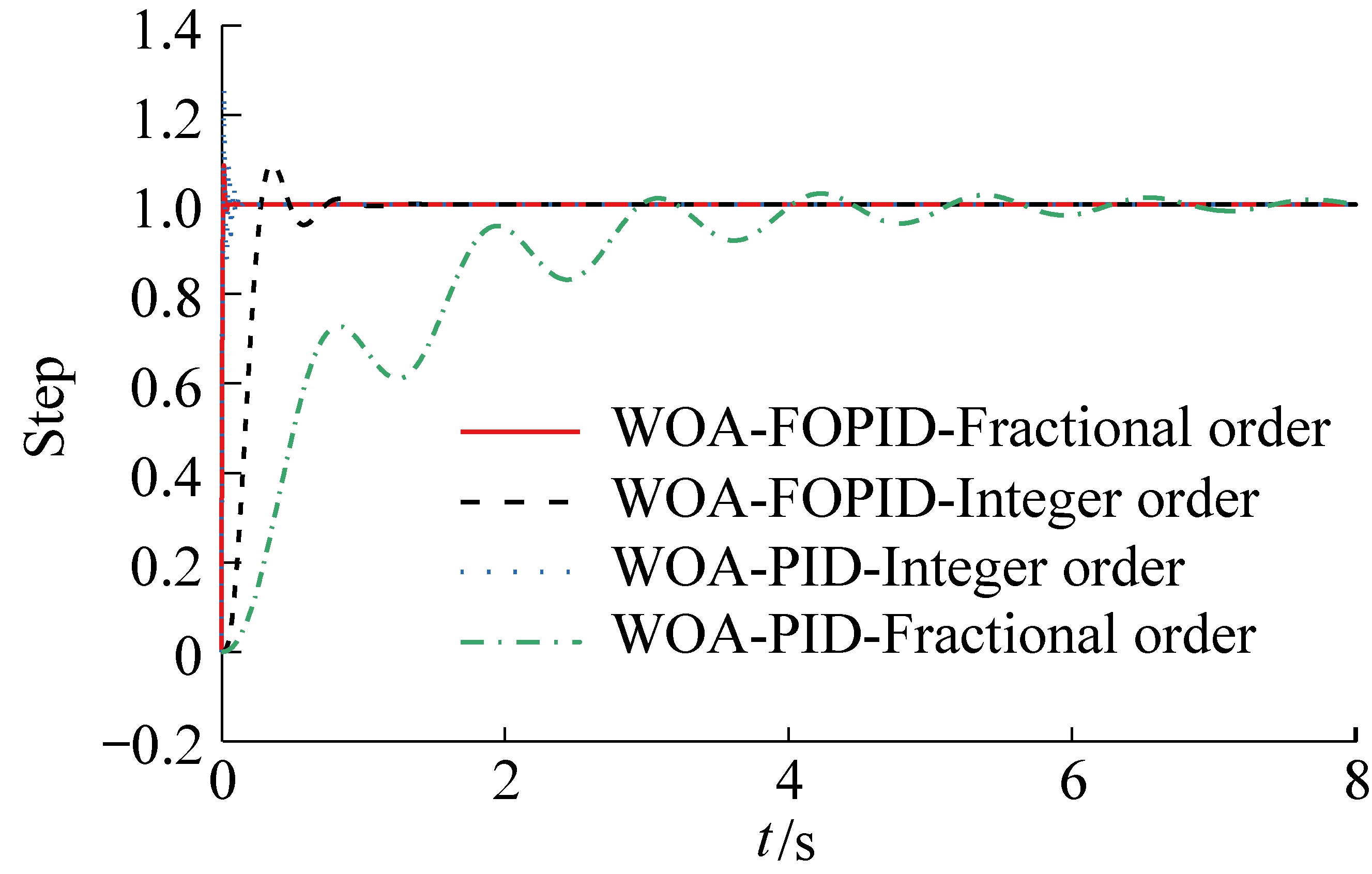
图9 DOA090470-1(1)液压缸不同组合策略控制效果阶跃响应
Fig.9 DOA090470-1(1) step response of control effect of different combination strategies of hydraulic cylinder
表4 DOA090470-1(1)液压缸不同组合策略和控制指标对比
Table 4 Comparison of different combination strategies and control indexes of DOA090470-1(1) hydraulic cylinder

组合动态指标标准方差超调/%稳定时间/sWOA-FOPID-Integer order0.130 709.500%0.68WOA-FOPID-Fractional order0.035 718.672%0.02WOA-PID-Integer order0.037 5325.780%0.09WOA-PID-Fractional order0.220 602.500%6.06
3)DOA090260-1液压缸的数学建模及仿真测试。根据液压油缸的相关参数见表5。DOA090260-1液压缸的整数阶数学模型[57-58]:
表5 DOA090260-1液压油缸参数
Table 5 DOA090260-1 hydraulic cylinder parameter
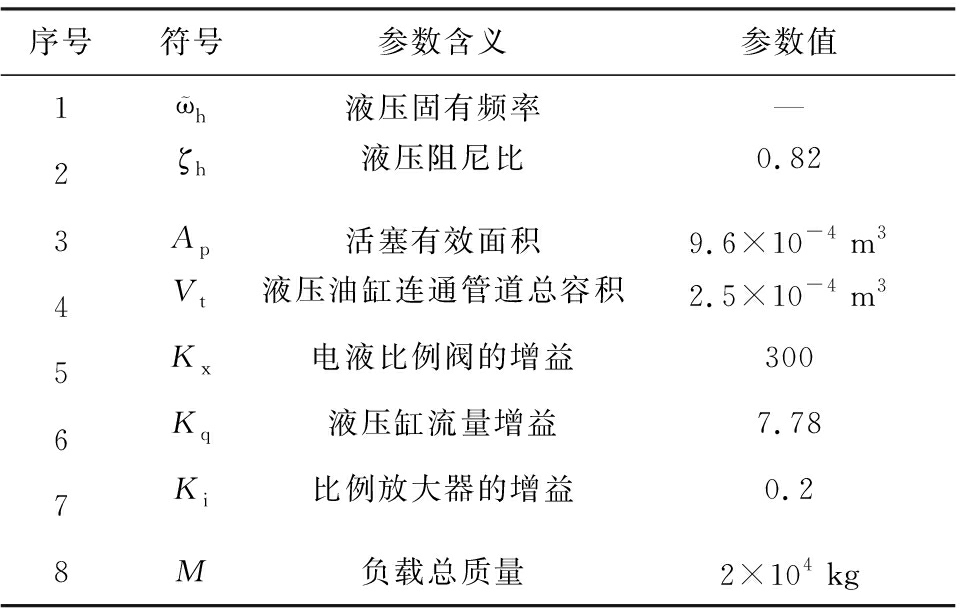
序号符号参数含义参数值1h液压固有频率—2ζh液压阻尼比0.823Ap活塞有效面积9.6×10-4 m34Vt液压油缸连通管道总容积2.5×10-4 m35Kx电液比例阀的增益3006Kq液压缸流量增益7.787Ki比例放大器的增益0.28M负载总质量2×104 kg

![]()
(22)
DOA090260-1液压缸的分数阶数学模型[59]:

(23)
整数阶PID控制器表达式[42-44]:
Gc=11.229 2+30 s-2+1.35×10-8 s
(24)
分数阶FOPID控制器表达式[45-47]:
Gc=0.475 8+27.228 3s-2.532 3+29.967 3s1.021 2
(25)
由图10和表6可知,在复杂系统中FOPID控制器对于分数阶被控对象有更好的控制效果,0.5 s就可以达到6.84%的超调量,从整体来看,FOPID控制器相较于PID控制器更具有稳定性,而PID的控制策略显示出的控制效果几乎一致,都在20%左右。

图10 WOA-FOPID-分数阶传递函数单位阶跃
Fig.10 WOA-FOPID-fractional transfer function unit step
表6 不同组合策略和控制指标对比
Table 6 Comparison of different combination strategies and control indicators
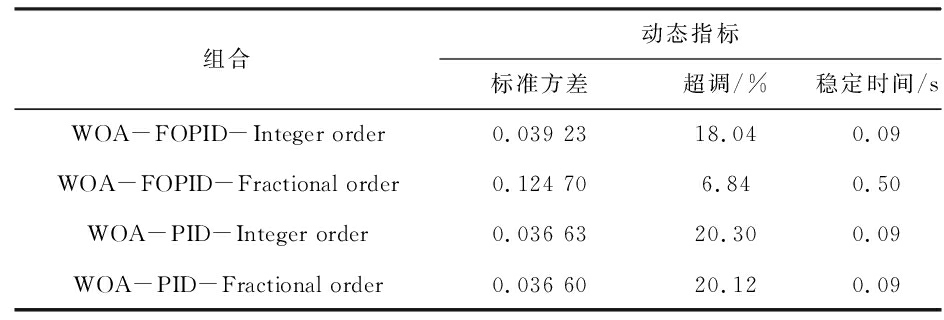
组合动态指标标准方差超调/%稳定时间/sWOA-FOPID-Integer order0.039 2318.040.09WOA-FOPID-Fractional order0.124 706.840.50WOA-PID-Integer order0.036 6320.300.09WOA-PID-Fractional order0.036 6020.120.09
1)针对钻锚机器人机械臂在复杂环境下能否实现孔位精准定位,利用FOPID控制微调特性应用于非线性控制对象,提出了一种基于鲸鱼算法整定FOPID控制参数的方法。基于独立关节控制理论,搭建了机械臂关节处液压马达/油缸单输入-单输出系统模型。
2)基于遗传算法、粒子群算法、鲸鱼算法,搜索算法4种智能优化算法,从标准方差、超调量、稳定时间3个动态指标进行对比,分析了液压马达/油缸的不同控制组合策略下阶跃影响下系统的控制效果。① 在WE9-62T-HR176-U液压马达数学建模及仿真测试中,FOPID控制器对于分数阶被控对象有更好的控制效果,超调量有所降低。从数据结果来看,WOA算法的寻优能力明显,对于分数阶被控对象在0.19 s就可以达到稳定,且超调量为3.49%,说明被控系统具有更好的稳定性,充分体现了分数阶FOPID控制器的优越性。② 在DOA090470-1(1)液压油缸数学建模及仿真测试中,PID控制分数阶作用于被控对象时尤为明显,6.06 s时才逐渐趋于稳定;在复杂系统中FOPID控制器对于分数阶被控对象有更好的控制效果,超调量为8.672%,在0.02 s内就可以趋于稳定。③ 在DOA090260-1液压缸的数学建模及仿真测试中,FOPID控制器对于分数阶被控对象有更好的控制效果,0.5 s就可以达到6.84%的超调量,从整体来看,FOPID控制器相较于PID控制器更具有稳定性,而PID的控制策略显示出的控制效果几乎一致,都在20%左右。验证了鲸鱼算法在整定参数中优异性能。
3)采用WOA-FOPID控制方法可以使钻锚机械臂末端空间定位控制精度更高。WOA-FOPID控制算法不仅可以提升控制系统的设计效率,而且还能提高控制系统的适应性能。
[1] 国家煤矿安全监察局.《煤矿机器人重点研发目录》[EB/OL].(2019-01-09)[2021-10-02].https://www.chinamine-safety.gov.cn/zfxxgk/fdzdgknr/tzgg/201901/t20190109_349156.shtml.
[2] 李芳玮,胡而已,张冬阳. 煤矿机器人研发应用现状及趋势[J]. 中国煤炭,2019,45(7):28-32.
LI Fangwei,HU Eryi,ZHANG Dongyang.Research and application status and trend of coal mine robots [J].China Coal,2019,45(7):28-32.
[3] 葛世荣,胡而已,裴文良. 煤矿机器人体系及关键技术 [J]. 煤炭学报,2020,45(1):455-463.
GE Shirong,HU Eryi,PEI Wenliang. Coal mine robot system and key technologies[J]. Journal of China Coal Society,2020,45(1):455-463.
[4] 刘 峰,曹文君,张建明,等.我国煤炭工业科技创新进展及“十四五”发展方向[J].煤炭学报,2021,46(1):1-15.
LIU Feng,CAO Wenjun,ZHANG Jianming,et al. The progress of scientific and technological innovation in China’s coal industry and the development direction of the 14th Five-Year Plan [J]. Journal of China Coal Society,2021,46(1):1-15.
[5] 王国法,刘 峰,庞义辉,等.煤矿智能化——煤炭工业高质量发展的核心技术支撑[J]. 煤炭学报,2019,44(2):349-357.
WANG Guofa,LIU Feng,PANG Yihui,et al. Coal mine intelligence-core technology support for high quality development of coal industry[J]. Journal of China Coal Society,2019,44(2):349-357.
[6] 王 虹,王建利,张小峰.掘锚一体化高效掘进理论与技术[J].煤炭学报,2020,45(6):2021-2030.
WANG Hong,WANG Jianli,ZHANG Xiaofeng. The theory and technology of integrated and efficient tunneling[J].Coal Journal,2020,45(6):2021-2030.
[7] 王国法,王 虹,任怀伟,等.智慧煤矿2025情景目标和发展路径[J].煤炭学报,2018,43(2):295-305.
WANG Guofa,WANG Hong,REN Huaiwei,et al. Smart coal mine 2025 scenario objectives and development path [J]. Journal of China Coal Society,2018,43(2):295-305.
[8] 吴 淼,李 瑞,王鹏江,等.基于数字孪生的综掘巷道并行工艺技术初步研究[J].煤炭学报,2020,45(S1):506-513.
WU Miao,LI Rui,WANG Pengjiang,et al. Preliminary study on parallel technology of fully mechanized excavation roadway based on digital twinning [J]. Journal of China Coal Society,2020,45(S1):506- 513.
[9] 康红普,王金华.巷锚杆支护理论与成套技术[M]. 北京:煤炭工业出版社,2007.
[10] 张 君,李玉贵. 含不确定性参数的锚杆钻机机械臂运动学误差分析[J]. 煤炭学报,2019,44(10):3223-3232.
ZHAGN Jun,LI Yugui.Kinematic error analysis of mechanical arm of anchor rig with uncertain parameters [J].Coal Journal,,2019,44(10):3223-3232.
[11] 张 君,张乾一,郭治富,等. 矿用锚杆钻机机械臂动力学不确定性分析[J]. 煤炭学报,2019,44(S1):351-360.
ZHANG Jun,ZHANG Qianyi,GUO Zhifu,et al. Dynamic uncertainty analysis of mechanical arm of mine anchor rig [J]. Journal of Coal,2019,44(S1):351-360.
[12] 金翠云,王建林,马江宁,等. 改进的PSO算法及其在PID控制器参数整定中的应用[J].电子测量与仪器学报,2010,24(2):141-141.
JIN Cuiyun,WANG Jianlin,MA Jiangning,et al. Improved PSO algorithm and its application in PID controller parameter tuning [J]. Journal of Electronic Measurement and Instruments,2010,24(2):141-141.
[13] FUKUDA Y,FENG M Q,NARTITA Y,et al. Vision-based displacement sensor for monitoring dynamic response using robust object search algorithm[J].IEEE Sensors Journal,2013,13(12):4725-4732.
[14] BRADLEY D A,SEWARD D W. The development,control and operation of an autonomous robotic excavator[J].Journal of Intelligent and Robotic System,1998,21(1):73-97.
[15] 孟 杰,杨海鹏,陈庆樟,等. 基于遗传算法优化的汽车半主动悬架PID控制仿真研究[J]. 现代制造工程,2013(6):92-96.
MENG Jie,YANG Haipeng,CHEN Qingzhang,et al,PID control simulation research of automobile semi-active suspension based on genetic algorithm optimization[J].Modern Manufacturing Engineering,2013(6):92-96.
[16] 李树江,赵 晨,苏锡辉,等. 基于遗传算法优化PID控制器参数的环境测试舱温湿度控制[J]. 南京理工大学学报,2017,41(4):511-518.
LI Shujiang,ZHAO Chen,SU Xihui,et al. Temperature and humidity control of environmental test cabin based on genetic algorithm to optimize PID controller parameters[J]. Journal of Nanjing University of Technology,2017,41(4):511-518.
[17] 叶 军,张苏敏,崔文华,等. 采用单值中智余弦相似度量和遗传算法的PID参数整定方法[P].中国:ZN109557811A,2019-01-22.
[18] 禹威威,申 远,徐小丽,等. 基于PSO的PID参数整定仿真与研究[J]. 重庆工商大学学报:自然科学版,2020,37(4):6.
YU Weiwei,SHEN Yuan,XU Xiaoli,et al. PID parameter tuning simulation and research based on PSO [J]. Journal of Chongqing University of Technology and Commerce:Natural Science Edition,2020,37(4):6.
[19] 张 天,张继荣,汤丽娜,等. 惯性权重余弦调整粒子群优化算法的PID参数整定方法[P].中国:ZL109696827A, 2019-04-30.
[20] 吴泽兵,王文娟,吕澜涛,等. 基于粒子群算法的自动送钻控制器仿真优化[J]. 石油矿场机械,2019,48(6):8.
WU Zebing,WANG Wenjuan,LYU Lantao,et al.The simulation optimization of automatic drilling controller based on particle swarm optimization algorithm[J].Oil Field Equipment,2019,48(6):8.
[21] 周蓓晨,张宏立. 基于拟混沌人群搜索算法PID参数优化研究[J]. 计算机仿真,2018,35(5):233-236.
ZHOU Beichen,ZHANG Hongli. Research on PID parameter optimization based on quasi-chaotic crowd search algorithm [J]. Computer Simulation,2018,35(5):233-236.
[22] MIRJALII S,LEWIES A.The whale optimization algorithm [J].Advances in Engineering Software,2016,95:51-67.
[23] 吴 坤,谭劭昌.基于改进鲸鱼优化算法的无人机航路规划[J].航空学报,2020,41(S2):107-114.
WU Kun,TAN Shaochang. UAV route planning based on improved whale optimization algorithm [J].Aerospace Journal,2020,41(S2):107-114.
[24] ZHAI Q,XIA X,FENG S,et al.Optimization design of lqr con-troller based on improved whale optimization algorithm[C] //2020 3rd International Conference on Information and Com puter Technologies(ICICT),2020:380-384
[25] VIJAYANAND R,DEVARAJ D.A Novel Feature Selection Method Using Whale Optimization Algorithm and Genetic Operators for Intrusion Detection System in Wireless Mesh Network[J]. IEEE Access,2020,8:56847-56854
[26] YIN C,CHEN Y Q,ZHONG S M. Fractional-order sliding mode based extremum seeking control of a class of nonlinear systems[J],Automatica,2014,50(12):3173-3181.
[27] U. AL-SAGGAF,R. MANSOURI,M. BETTAYEB,et al. Mun-awar. Robustness Improvement of the Fractional order LADRC scheme for Integer High order system[J]. IEEE Transactions on Industrial Electronics,2021,68(9):8572-8581.
[28] SHENG Y,BAI W,XIE Y. Fractional-order sliding mode control for hypersonic vehicles with neural network disturbance compensator[J]. Nonlinear Dynamics,2021,103:849-863.
[29] I. Podlubny. Fractional-order systems and fractionalord controller[J]. Mathematics in Science and Engineering,1999,198:243-260.
[30] XIANG W A,Sl A,Yin W B. Stability analysis of Riemann-Liouville fractional-order neural networks with reaction-diffusion terms and mixed time-varying delays[J]. Neurocomputing,2021(431):169-178.
[31] LABBADI M,BOUKAL Y,CHERKAOUI M. High order fractional controller based on PID-SMC for the QUAV under uncertainties and disturbance[M]. Advanced Robust Nonlinear Control Approaches for Quadrotor Unmanned Aerial Vehicle,2022.
[32] DAWEI,DING F,LIU N,et al. Stabilization of uncertain fraction-al memristor chaotic time-delay system based on fractional order sliding mode control[J]. Journal of Harbin Institute of Technology(New Series),2020,27(4):78-87.
[33] MOLTUMYRA H,RAGAZZON M,GRAVDAHL J T. Fractional-order co-ntrol:nyquist constrained optimization[J].IFAC-PapersOnLine,2020,53(2):8605-8612.
[34] PETERO J,SHAIKH A S,IBRAHIM M O,et al. Analysis and dyna-mics of fractional order mathematical model of covid-19 in nigeria using atangana-baleanu operator[J]. Computers,Materials and Continua,2021,66(2):1823-1848.
[35] MUSARRATM N,FEKIH A. A fractional order sliding mode cont-rol-based topology to improve the transient stability of wind energy systems[J]. International Journal of Electrical Power & Energy Systems,2021,133(107306):1-12.
[36] ORESANYA B O,SI G,GUO Z,et al. Mathematical analysis and emulation of the fractional-order cubic flux-controlled memristor[J]. Alexandria Engineering Journal,2021,60(5):4315-4324.
[37] 王 虹,尤秀松,李首滨,等.基于遗传算法与BP神经网络的支架跟机自动化研究[J].煤炭科学技术,2021,49(1):272-277.
WANG Hong,YOU Xiusong,LI Shoubin,et al.Research on automation of support based on genetic algorithm and BP neural network[J].Coal Science and Technology,2021,49(1):272-277.
[38] 马宏伟,姚 阳,薛旭升,等.基于多传感器组合的钻锚机器人机身定位方法研究[J].煤炭科学技术,2021,49(1):278-285.
MA Hongwei,YAO Yang,XUE Xusheng,et al.Research on body positioning method of drill-anchor robot based on multi-sensor combination[J].Coal Science and Technology,2021,49(1):278-285.
[39] 褚鼎立,陈 红,王旭光.基于自适应权重和模拟退火的鲸鱼优化算法[J].电子学报,2019,47(5):992-999.
CHU Dingli,CHEN Hong,WANG Xuguang. Whale optimization algorithm based on adaptive weight and simulated annealing[J]. Electronics,2019,47(5):992-999.
[40] BUTTI D,MANGIPUDI S K,RAYAPUDI S R. An improved wh-ale optimization algorithm for the design of multi-machine power system stabilizer[J]. International Transactions on Electrical Energy Systems,2020,30(5).1-29
[41] SEMMARI H,MAURAN S,STITOU D. Experimental validation of an analytical model of hydraulic motor operating under variable electrical loads and pressure heads[J]. Applied Energy,2017,206(15):1309-1320.
[42] DASGUPTA K,Mukherjee A,Maiti R. Modeling and dynamics of epitrochoid generated orbital rotary piston lsht hydraulic motor:a bondgraph approach[J]. Journal of Manufacturing Science & Engineering,1996,118(3):415-421.
[43] MAITI D,BISWAS S,KONAR A. Design of a fractional order pid controller using particle swarm optimization technique[J]. International Journal of Advanced Manufacturing Technology,2008,58(5-8):521-531.
[44] CAPONETTO R,JOSÉ TENREIRO MACHADO,MURGANO E,et al. Model order reduction:a comparison between integer and non-integer order systems approaches[J]. Entropy,2019,21(9):876.
[45] DO T C,TRAN D T,DINH T Q,et al. Tracking control for an electro-hydraulic rotary actuator using fractional order fuzzy pid controller[J]. Electronics,2020,9(6):926-942.
[46] 马方军. 基于分数阶的单相PWM整流器建模与控制研究[D].焦作:河南理工大学,2016.
MA Fangjun. Modeling and control of single-phase PWM rectifier based on fractional order [D].Jiaozuo:Henan University of Technology,2016.
[47] 刘 东. 电液位置伺服系统自适应控制方法研究[D]. 哈尔滨:哈尔滨工业大学,2008.
LIU DongResearch on adaptive control method of electro-hydraulic position servo system[D]Harbin:Harbin University of Technology,2008.
[48] BABA I A,NASIDI A. Fractional order epidemic model for the dynamics of novel COVID-19[J]. AEJ-Alexandria Engineering Journal,2021.60(1):537-548.
[49] DIMEAS I,IVO Petrá,PSYCHALINOS C.New analog implementation technique for fractional-order controller:A DC motor control[J]. AEU-International Journal of Electronics and Communications,2017,78:192-200.
[50] TOLBA M F,ABOALNAGA B.Said L A,et al. Fractional Order Integrator/Differentiator:FPGA implementation and FOPID Controller Application[J]. AEU-International Journal of Electronics and Communications,2018,98:220-229.
[51] Elkhazali R. Fractional-order PI λD controller design[M]. Pergamon Press,Inc.2013.
[52] MAAMAR B,RACHID M. IMC-PID-fractional-order-filter controll-ers design for integer order systems[J]. Isa Transactions,2014,53(5):1620-1628.
[53] REN H P,FAN J T,KAYNAK O. Optimal Designof a fractional order pid controller for a pneumatic position servo system[J]. IEEE Transactions on Industrial Electronics,2019,66(8):6220-6229.
[54] ZAMANI M,KARIMI-GHARTEMANI M,SADATI N,et al. De-sign of a fractional order PID controller for an AVR usingparticle swarm optimization[J]. Control Engineering Practice,2009,17(12):1380-1387.
[55] DING Y,XU J,CAO J,et al. Mathematical modeling about nonlinear delayed hydraulic cylinder system and its analysis on dynamical behaviors[J]. Discrete and Continuous Dynamical Systems-Series S,2017,10(5):943-958.
[56] 湛从昌,邓江洪,陈奎生. 低摩擦高频响变间隙密封液压缸研究[J]. 机械工程学报,2015,51(24):161-167.
ZHAN Congchang,DENG Jianghong,CHEN Kuisheng.Low friction high frequency response clearance seal hydraulic cylinder research [J].Mechanical Engineering,2015,51(24):161-167.
[57] 薛定宇.薛定宇教授大讲堂(卷Ⅳ):MATLAB最优化计算[M]. 北京:清华大学出版社,2020.