
安全科学与工程

煤矿动力灾害的防治工作一直以来都是矿山安全领域研究热点之一[1-2]。自发现煤岩破裂中磁信号异常现象后,专家学者开始研究利用煤体破裂所产生磁信号来开展矿山动力灾害的监测预警工作。文献[3-5]指出磁信号强度与裂纹扩展速度、试样强度、裂纹长度等因素密切相关,裂纹扩展速度越高、试样强度越大、裂纹长度越长所释放磁信号也就越强。我国学者何学秋[6-7]借助试验手段研究煤体破坏过程中磁信号时、频谱特征,提出了磁信号可能的产生机制,如压电效应、压磁效应、摩擦效应、电荷分离及变速运动、电偶极子震荡等。李成武等[8-10]研究了煤体静载破坏下磁场信号特征并借助RFPA2D数值模拟软件开展煤体静载破坏磁信号数值模拟研究,他指出煤体静载破坏磁信号存在四阶段特征,按信号变换趋势依次可划分为“零值-缓慢上升-跳跃增加-平稳变化”。王恩元等[11-12]试验研究了煤体破裂磁信号时域上阶段性变化特征,得到从时间序列来看煤矿灾害发生前磁信号存在明显的异常特征,可据此开展动力灾害的监测预警。文献[13-15]通过实验手段研究了瓦斯吸附作用对煤体结构的影响,此外,设计了含瓦斯煤体破裂试验并测试煤破裂中磁信号,分析得出瓦斯对于煤体破坏所产生的磁场信号具有弱化作用。经上分析可知国内外学者对于煤体破裂磁信号的产生机理、演变特征、影响因素研究较多,然研究结果尚未达成统一,有必要对其相关基础理论做进一步研究。
前人已证明,煤体破裂磁信号强度与煤体内裂纹扩展密切相关,然而由于试样裂纹扩展存在捕捉难、量化难等问题,很少有学者实现裂纹扩展与磁信号之间的量化研究。谢和平[16-19]指出试样损伤演化过程相当于材料裂纹演化过程,试样裂纹扩展是随机分布、无序的,且在不同尺度下具有一定自相似性,其具有分形特征,可利用分形理论对裂纹形态特征研究。一些学者借助分形理论实现了煤岩体破坏中裂纹的量化研究,据此完成了裂纹与其他参量的量化分析,例如加载速率愈快,裂纹扩展实测平均速度愈高,裂纹面积,形态随着载荷增加具有明显的阶段性 [20-23]。
基于此,笔者借助数值模拟软件模拟试样静载破坏后裂纹形态特征及磁信号特征,并结合分形理论量化分析了裂纹形态与磁信号之间关系,研究结果对于煤岩体破坏过程中磁信号产生机制的研究具有重要意义,对于推动矿山动力灾害监测预警技术的发展具有一定的现实意义。
文献[9]借助RFPA软件建立了力、能量与磁信号之间关系模型,该模型中包含了损伤与破坏单元格及磁脉冲之间函数关系式,具体如下:
(1)
(2)
式中:D为损伤量;∑Ni为加载至i步时单元格破坏累积数量,个;NZ为试样发生断裂破坏后破坏单元格总数,个;∑Mi为加载至i步时磁脉冲累积释放数,个;MZ为试样断裂破坏后总磁脉冲数,个。
整个试样所含弹性能可由式(3)计算
![]()
(σ1iσ2i+σ1iσ3i+σ2iσ3i)]
(3)
式中,WEi为第i步试样累积弹性能,J;σ1i、σ2i、σ3i为加载至第i步时第j个单元格3个方向应力,MPa;Ej为第j个单元格弹性模量,MPa;μj为j个单元格泊松比;NT为单元格总数量。
煤体破坏后所释放磁能由式(4)计算:
EMi=γ(Fixi-WEi)
(4)
式中,EMi为第i步时释放总磁能,J;γ为磁能占比;Fi为第i步时载荷,N;xi为第i步时轴向位移,m。
裂纹是一种微观与宏观具有一定相似性的无规则分形结构,而分形维数可表征裂纹弯曲复杂程度及裂纹疏密程度。盒维数为最常用图像分形维数计算方法,它的主旨思想为利用一系列边长不等的正方形小盒去覆盖整个含裂纹图像,之后统计非空盒子个数,根据非空盒子个数及盒子边长即可得到裂纹盒维数,其可由式(5)计算:
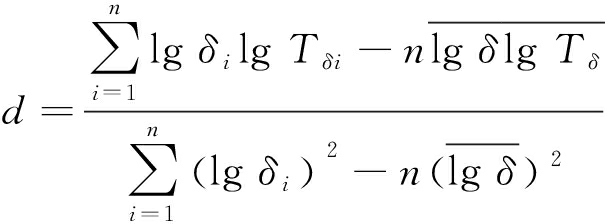
(5)
式中:d为裂纹盒维数;δ为正方形小盒边长,m;δi为选择第i种正方形小盒边长,m;Tδ为用边长为δ小正方形填充下非空盒子数量,个;Tδi为用边长为δi小正方形填充下非空盒子数量,个;n为n种边长不等的正方形小盒。
为保证盒维数计算准确性,首先需要对图像进行预处理以保证图像大小一致,然后选择合理灰度值作为阈值,自动识别裂纹与非裂纹部分,对裂纹非裂纹部分做二值化处理,其中裂纹部分设置为黑色,非裂纹部分设置为白色。用不同边长的盒子填充二值化处理后图片,并统计灰度值非零盒子的个数,记作非空盒子数,最后结合式(5)计算图像中裂纹盒维数。
利用Matlab编程实现裂纹自主识别及分形盒维数计算,具体流程如图1所示。
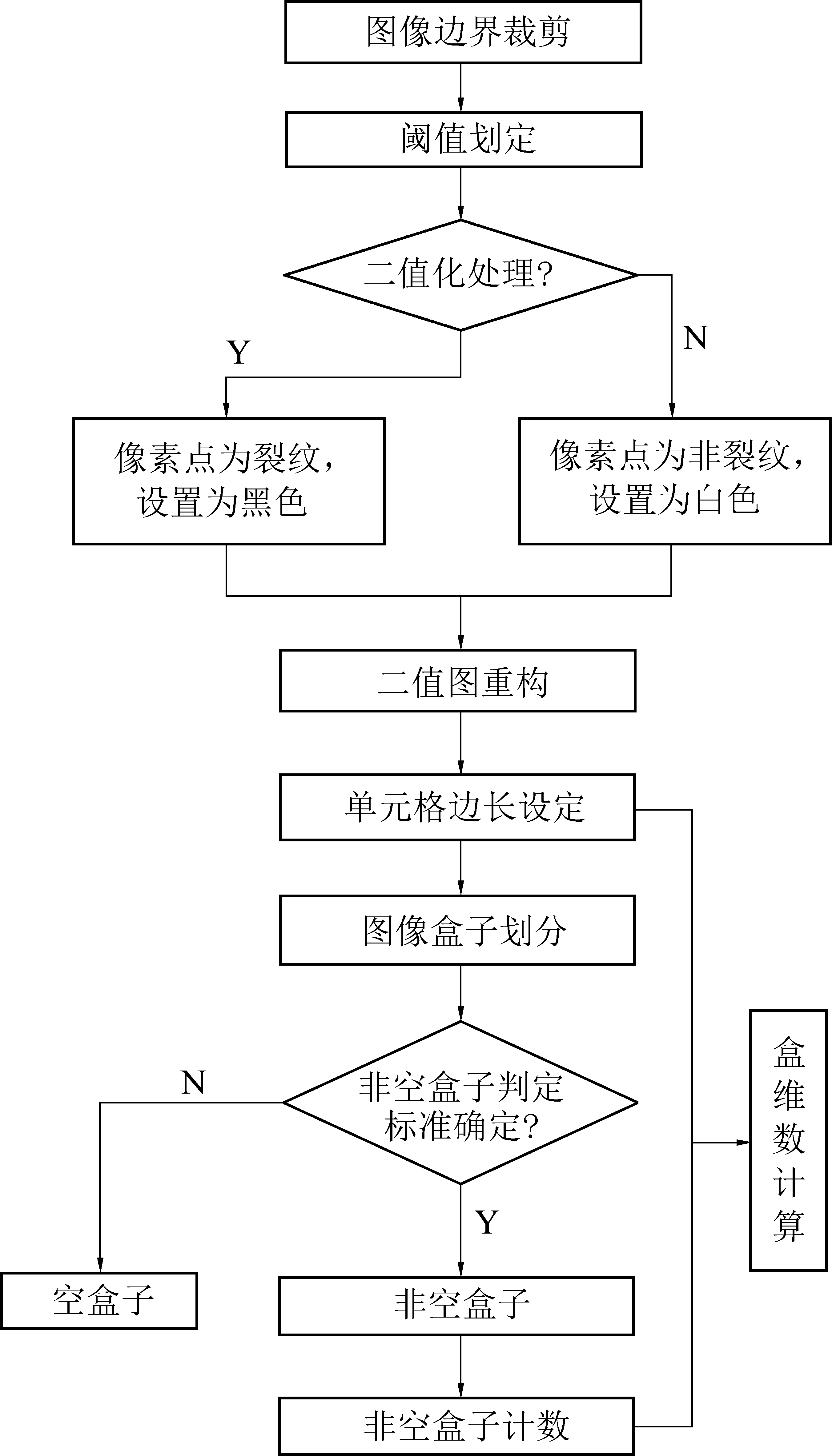
图1 盒维数计算流程
Fig.1 Calculation process of box dimension
文献[8]指出煤体静载破坏主要呈现弹-脆性破坏形式,失稳前以弹性变形为主,达极限强度时,瞬间发生脆性断裂破坏。因脆性断裂发生发展较快,无法准确记录其裂纹扩展规律及裂纹整体形态特征。因此,利用RFPA2D软件模拟试样静载破坏中裂纹扩展规律,并结合力-磁耦合模型,模拟试样破坏中磁信号变化特征。
共设置了7组模拟试验,依次为:不含层理模型、含(1、3、5条)垂直层理模型及含(1、3、5条)水平层理模型(图2)。模型依据相关标准设定,长度50 mm,高度100 mm,共包含20 000个单元格。

图2 模型建立
Fig.2 Design of models
层理与非层理部分力学性质差别较大,本文中2部分参数设置见表1。以位移方式加载,单步增量0.01 mm,总步数100步,总位移1 mm。
表1 力学参数设计
Table 1 Design of mechanical parameters
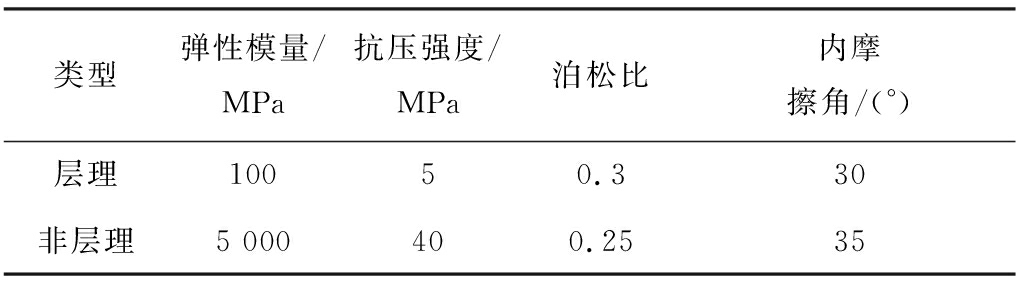
类型弹性模量/MPa抗压强度/MPa泊松比内摩擦角/(°)层理10050.330非层理5 000400.2535
2.3.1 破坏特征分析
分析发现所建7个模型均呈弹-脆性破坏形式,以不含层理试样为例分析如图3所示。

图3 试样破坏过程
Fig.3 Failure process of the sample
由图3可得,不含层理试样在加载至31步时,看到试样出现了显著的内部损伤,37步时出现了一些微裂纹,而加载至38步时,试样瞬间发生脆性破坏,其裂纹呈单斜面状,且在裂纹两侧出现一定范围塑性破坏区。其余6个含层理试样失稳破坏后结果如图4所示。

图4 含层理试样裂纹形态
Fig.4 Crack shape of sample with bedding
由图4可知,含垂直层理试样主要沿层理面呈劈裂状破坏,其裂纹沿层理面扩展,而含水平层理试样裂纹呈发散状,无明显规律性。对比文献[8]中试验所得结果(图5)可知本次数值模拟所得结果是可靠的。

图5 试验中煤体静载破坏形态[10]
Fig.5 Failure pattern of sample in laboratory experiment[10]
该试验中原煤型煤试样相关参数见表2。
表2 试验中煤体试样参数
Table 2 Parameters of coal samples in experiment
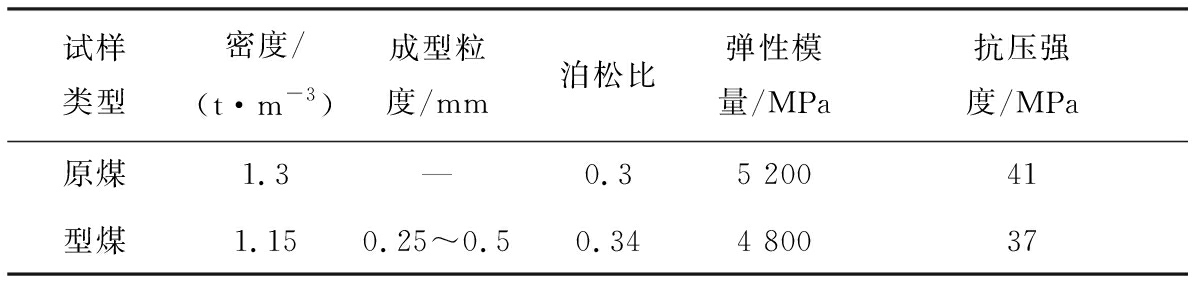
试样类型密度/(t·m-3)成型粒度/mm泊松比弹性模量/MPa抗压强度/MPa原煤1.3—0.35 20041型煤1.150.25~0.50.344 80037
2.3.2 磁信号特征分析
借助力磁耦合模型与RFPA软件模拟得到7个模型破坏后磁脉冲数量及释放总磁能量,对其进行统计见表3。
表3 试样磁脉冲及磁能
Table 3 Magnetic pulse and magnetic energy of samples
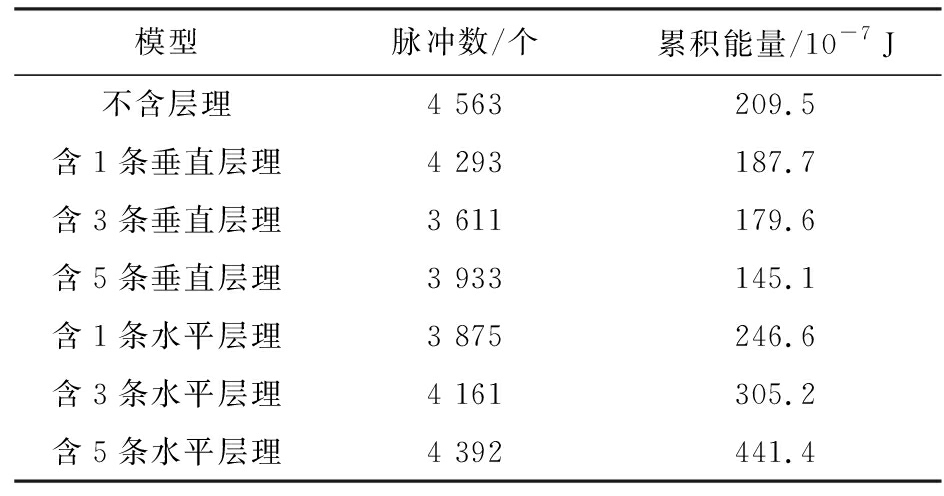
模型脉冲数/个累积能量/10-7 J不含层理4 563209.5含1条垂直层理4 293187.7含3条垂直层理3 611179.6含5条垂直层理3 933145.1含1条水平层理3 875246.6含3条水平层理4 161305.2含5条水平层理4 392441.4
由表3可得,对于含水平层理试样,层理数量与磁脉冲及磁能呈正相关关系,对于含垂直层理试样,层理数量与磁能呈负相关关系,与磁脉冲数关系不显著。
前文已证数值模拟所得结果与前人试验所得结果一致,从模拟所得试样破坏结果图出发,分析并计算试样破坏后裂纹盒维数特征,以此实现含不同层理性质试样裂纹的量化处理。
基于图3及图4中试样失稳破坏后裂纹图像,根据盒维数计算流程分别对7个模拟结果图进行处理,结果如图6所示,其中黑色部分代表裂纹发展区域。后计算各个试样裂纹分形盒维数,其结果如图7所示。提取图7中各个试样裂纹盒维数,结果见表4。由表4可得,不含层理试样裂纹盒维数最低,含层理试样裂纹盒维数相对较高。因含垂直层理与水平层理试样破坏特征差别较大,不能进行统一分析,分别单独分析两者盒维数与层理数量间关系,结果如图8所示。

图6 试样失稳破坏后裂纹图像二值化处理结果
Fig.6 Binarization processing of crack image of coal after coal failure
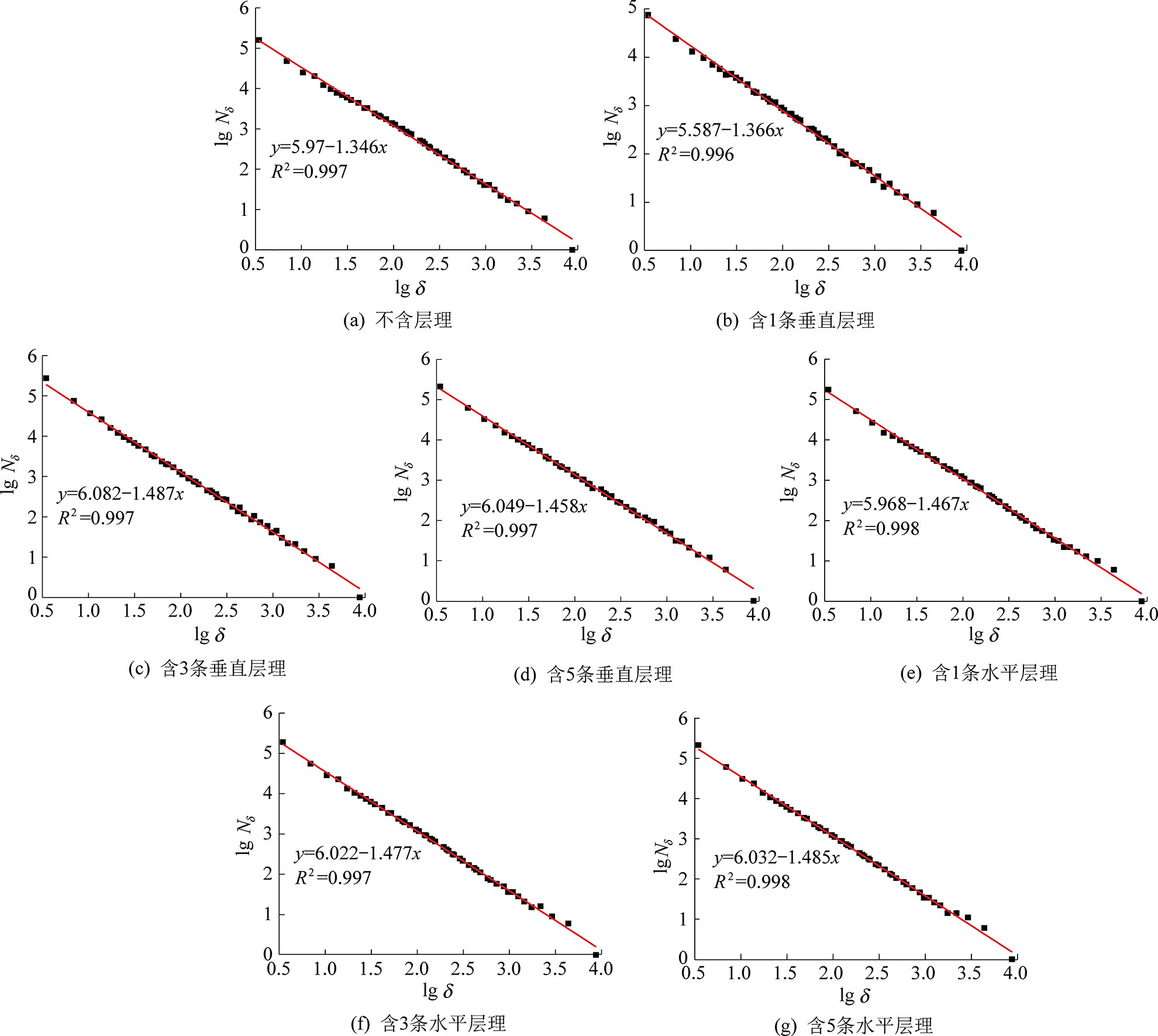
图7 盒维数拟合结果
Fig.7 Linear fitting of box dimension
表4 盒维数统计
Tab 4 Statistical results of box dimensions
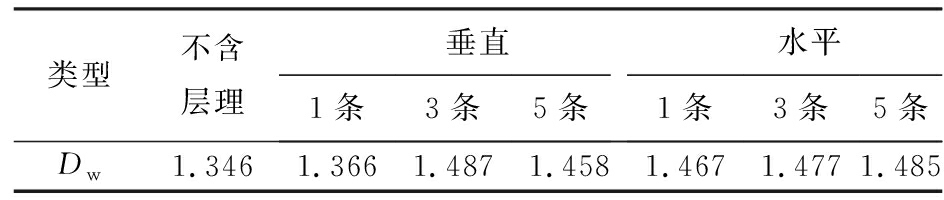
类型不含层理垂直水平1条3条5条1条3条5条Dw1.3461.3661.4871.4581.4671.4771.485
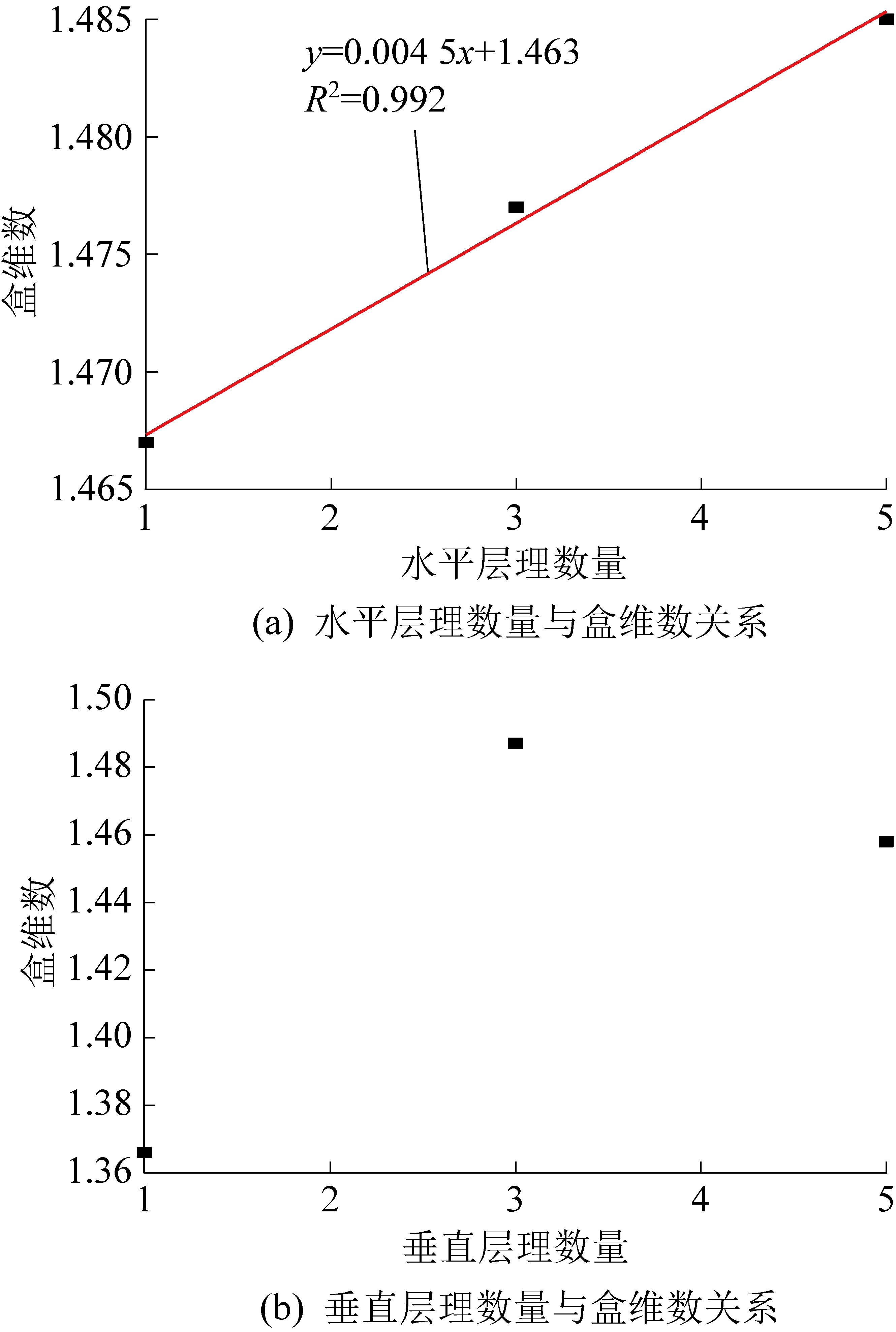
图8 层理与裂纹盒维数关系
Fig.8 Relation between bedding and box dimension
由图8可得,对于含水平层理试样,层理数量与裂纹盒维数之间呈现出很好线性正相关关系,随层理数增加,盒维数线性增加。而对于含垂直层理试样,层理数量与盒维数之间不存在显著的关联特性。分析其原因为:由图6e—图6g可知,含水平层理试样,层理数量越多,试样破坏后裂纹越复杂,破碎区面积越大,其规律性较明显。含垂直层理试样裂纹主要沿层理面发展,且随层理数增加,裂纹密集程度越高,但其弯曲度复杂程度越简单,且由图6b—图6d可得其非层理部分裂纹扩展无规律可寻,这样两者间规律性就不显著。
1)含水平层理试样。对于含水平层理试样,其裂纹盒维数与磁能及脉冲数之间关系,如图9所示。由图9可得,含水平层理试样裂纹盒维数与磁脉冲数、磁能之间均呈现出很好的正线性相关关系,随裂纹盒维数增加试样破坏所释放总脉冲数及总磁能线性增加。

图9 含水平层理试样盒维数与磁信号关系
Fig.9 Relation between magnetic signals and box dimension of samples with horizontal bedding
2)含垂直层理试样。对于含垂直层理试样,其裂纹盒维数与总磁脉冲数及总磁能之间关系,如图10所示。由图10可得,含垂直层理试样裂纹盒维数与磁脉冲数之间呈现出较好的负线性相关关系,随裂纹盒维数增加磁脉冲数呈线性减小,而其与磁能之间不存在显著相关关系。分析其原因为:裂纹盒维数为反映裂纹几何特征如复杂程度、疏密程度等的参数值,且垂直层理试样破坏时其裂纹主要沿层理面扩展,相对简单,层理数量越多规律性越明显,这样裂纹复杂程度也就越小其盒维数也就会越低。因含垂直层理试样破坏时其非层理部分裂纹扩展具有一定随机性,因此其能量规律就难以捕捉。
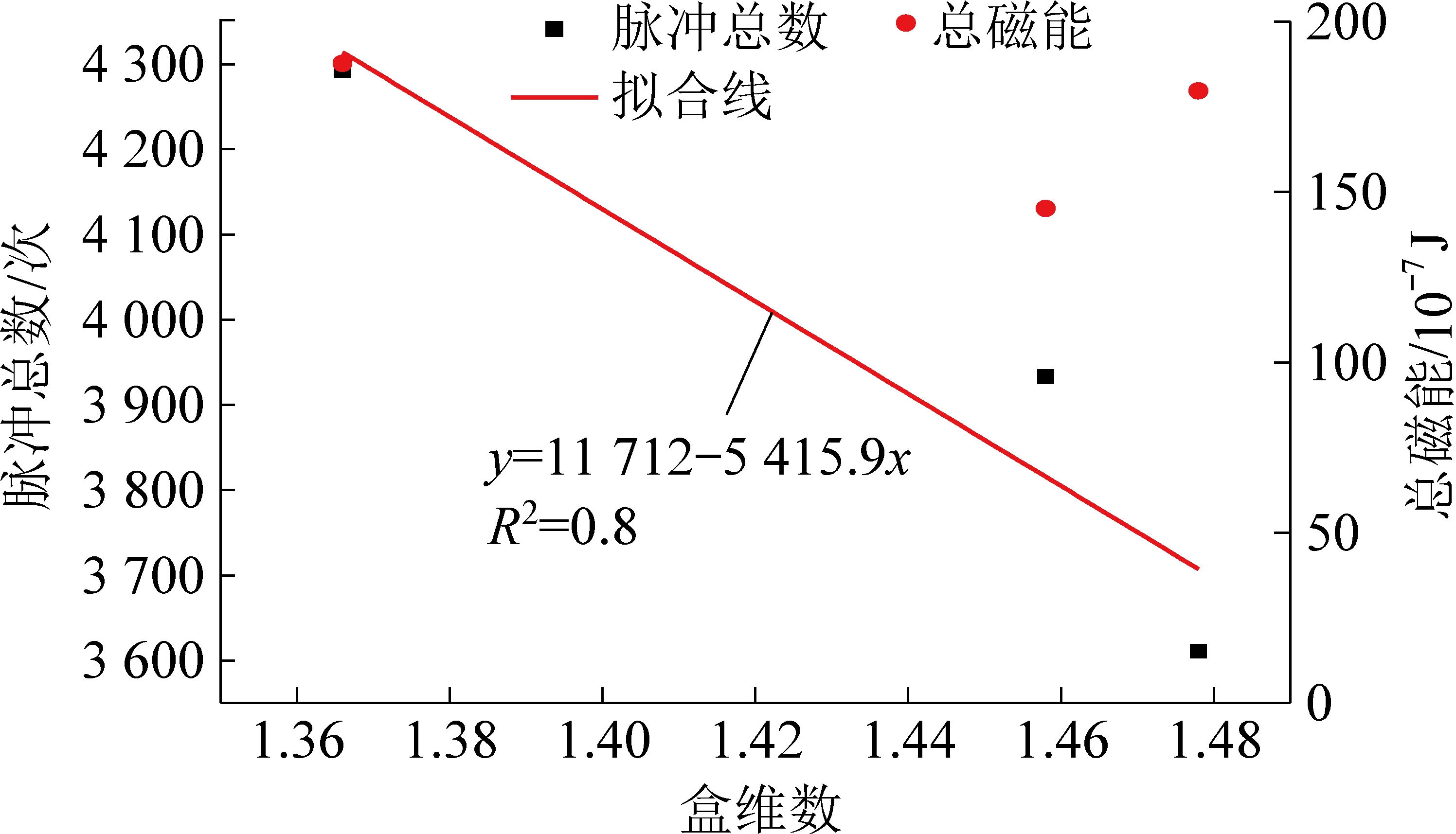
图10 含垂直层理试样盒维数与磁信号关系
Fig.10 Relation between magnetic signals and box dimension of samples with vertical bedding
1)不含层理试样失稳破坏后裂纹盒维数最低,含水平层理试样,裂纹盒维数与层理数量呈线性正相关关系,含垂直层理试样,裂纹盒维数与层理数量之间无显著相关关系。
2)含水平层理试样,层理数量与磁脉冲及磁能呈正相关关系,对于含垂直层理试样,层理数量与磁能呈负相关关系,与磁脉冲数关系不显著。
3)对于含水平层理试样,裂纹盒维数均与磁脉冲数、磁能呈现出很好的正线性相关关系;而含垂直层理试样,裂纹盒维数与磁脉冲数呈现较好的负线性相关关系,与磁能之间不存在相关关系。
[1] 李琰庆,杨 科,秦汝祥,等.煤与瓦斯突出煤层群安全高效开采技术体系与展望[J].煤炭科学技术,2020,48(3):167-173.
LI Yanqing. YANG Ke, QIN Ruxiang, et al. Technical system and prospect of safe and efficient mining of coal and gas outburst coal seams[J]. Coal Science and Technology, 2020,48(3):167-173.
[2] 马斌文,邓志刚,赵善坤,等.钻孔卸压防治冲击地压机理及影响因素分析[J].煤炭科学技术,2020,48(5):35-40.
MA Binwen. DENG Zhigang, ZHAO Shankun, et al. Analysis on the mechanism and influencing factors of drilling pressure relief to prevent rock burst[J]. Coal Science and Technology, 2020,48(5):35-40.
[3] FRID, V, RABINOVITCH, A, BAHAT, D. Fracture induced electromagnetic radiation[J]. Journal of Physics D Applied Physics, 2003, 36(13):1620-1628.
[4] FRID V, RABINOVITCH A, BAHAT D. Crack velocity measurement by induced electromagnetic radiation[J]. Physics LETTERS A, 2006, 356(2):160-163.
[5] RABINOVITCH A, FRID V, BAHAT D. Parametrization of electromagnetic radiation pulses obtained by triaxial fracture of granite samples[J]. Philosophical Magazine Letters, 1998, 77(5):289-293.
[6] 何学秋, 王恩元, 聂百胜,等. 煤岩流变电磁动力学[M]. 北京:科学出版社,2003.
[7] 何学秋, 聂百胜, 王恩元, 等. 矿井煤岩动力灾害电磁辐射预警技术[J]. 煤炭学报, 2007, 32(1):56-59.
HE Xueqiu. NIE Baisheng, WANG Enyuan, et al. Electromag-netic emission forecasting technology of coal or rock dynamic disasters in mine[J]. Journal of China Coal Society, 2007, 32(1):56-59.
[8] LI C W, FU S, GUAN C, et al. Characteristics and generation mechanism of ULF magnetic signals during coal deformation under uniaxial compression[J]. Journal of Geophysics and Engineering,2018,15(4):1137-1145.
[9] 李成武,付 帅,王菲茵,等. 层理对煤体破坏中磁信号特征影响的数值模拟研究[J]. 煤炭学报,2018,43(8):2225-2232.
LI Chengwu, FU Shuai, WANG Feiyin, et al. Numerical simulation of the influence of bedding on characteristics of magnetic signals emitted from coal failure[J]. Journal of China Coal Society, 2018,43(8):2225-2232.
[10] 李成武,付 帅,解北京,等.煤体静载破坏中低频磁场变化特征及产生机制研究[J].岩土力学,2019,40(2):481-488.
LI Chengwu, FU Shuai, XIE Beijing, et al. Characteristics and generation mechanism of low-frequency magnetic field generated during the damage of coal by static load. [J]. Rock and Soil Mechanics,2019,40(2):481-488.
[11] 刘晓斐, 王恩元, 何学秋. 孤岛煤柱冲击地压电磁辐射前兆时间序列分析[J]. 煤炭学报, 2010, 35(S1):15-18.
LIU Xiaofei, WANG Enyuan, HE Xueqiu. Time series analysis of electromagnetic radiation precursor of rockburst in gob-surrounded coal pillar[J]. Journal of China Coal Society, 2010, 35(S1):15-18.
[12] 胡少斌, 王恩元, 李忠辉,等. 受载煤体电磁辐射动态非线性特征[J]. 中国矿业大学学报, 2014, 43(3):380-387.
HU Shaobin, WANG Enyuan, LI Zhonghui, et al. Norlinear dynamic characteristics of electro- magenetic radiation during loading coal[J]. Journal of China University of Mining & Technology, 2014, 43(3):380-387.
[13] NIE B S, FAN P H, LI X C. Quantitative investigation of anisotropic characteristics of methane-induced strain in coal based on coal particle tracking method with X-ray computer tomography[J]. Fuel, 2018, 214:272-284.
[14] HE X Q, NIE B S, CHEN W X, et al. Coal macromolecular structural characteristic and its in uence on coalbed methane adsorption[J]. Fuel, 2018, 222:687-694.
uence on coalbed methane adsorption[J]. Fuel, 2018, 222:687-694.
[15] HE X Q, NIE B S, CHEN W X, et al. Research progress on electromagnetic radiation in gas-containing coal and rock fracture and its applications[J]. Safety Science, 2012, 50(4):728-735.
[16] 谢和平. 分形—岩石力学导论[M].北京:科学出版社,1996.
[17] 谢和平. 分形几何及其在岩土力学中的应用[J]. 岩土工程学报, 1992, 14(1):14-24.
XIE Heping. Fractal geometry and its application to rock and soil materials[J]. Chinese Journal of Geotechniccal Engineering, 1992, 14(1):14-24.
[18] 谢和平, 陈至达. 分形(fractal)几何与岩石断裂[J]. 力学学报, 1988,20(3):264-271.
XIE Heping, CHEN Zhida. Fractal geometry and fracture of rock[J]. Acta Mechanica Sinica, 1988,20(3):264-271.
[19] 李子文, 郝志勇, 庞 源,等. 煤的分形维数及其对瓦斯吸附的影响[J]. 煤炭学报, 2015, 40(4):863-869.
LI Ziwen, HAO Zhiyong, PANG Yuan, et al. Fractal dimensions of coal and their influence on mwthance adsorption[J]. Journal of China Coal Society, 2015, 40(4):863-869.
[20] 秦 楠,张作良,冯学志,等. 蠕变作用后裂隙类岩石单轴强度和裂纹扩展规律研究[J]. 煤炭科学技术, 2020,48(12):244-249.
QIN Nan,ZHANG Zuoliang,FENG Xuezhi,et al. Study on uniaxial strength and crack propagation law of cracked similar rock after creep[J]. Coal Science and Technology, 2020, 48(12): 244-249.
[21] 曹 富, 杨丽萍, 李 炼,等. 压缩单裂纹圆孔板(SCDC)岩石动态断裂全过程研究[J]. 岩土力学, 2017, 38(6):1573-1582.
CAO Fu, YANG Liping, LI Lian, et al. Research on whole dynamical fracture process of rock using single cleavage drilled compression(SCDC) specimen[J]. Rock and Soil Mechanics, 2017, 38(6):1573-1582.
[22] 王传洋, 杨春和, 衡 帅,等. 压缩荷载下泥岩裂缝演化规律的CT试验研究[J]. 岩土力学, 2015, 36(6):1591-1597.
WANG Chuanyang, YANG Chunhe, HENG Shuai, et al. CT test for evolution of mudstone fractures under compressive load[J]. Rock and Soil Mechanics, 2015, 36(6):1591-1597.
[23] 彭守建, 许 江, 张超林,等. 含瓦斯煤岩剪切破断过程中裂纹演化及其分形特征[J]. 煤炭学报, 2015, 40(4):801-808.
PENG Shoujian, XU Jiang, ZHANG Chaolin, et al. Fractal characteristics of crack evolution in gas-bearing coal under shear loading[J]. Journal of China Coal Society, 2015, 40(4):801-808.