0 引 言
冲击地压是地下采动过程中煤岩系统发生失稳导致的岩石动力灾害，冲击地压影响范围较广且危害程度高，因此研究冲击地压的产生机理是重中之重。对于冲击地压机理的研究有经典的刚度理论、强度理论、能量理论、变形系统失稳理论、突变理论和扰动响应失稳理论等[1]，但诸多理论对于冲击地压的分析大部分是从准静态的角度分析煤岩体的能量或应力场的变化；潘俊锋等[2]认为冲击地压是岩石系统的静态孕育在动载扰动下诱发的动力失稳现象；冲击地压是煤岩系统在准静态下积累能量，满足失稳判据达到临界状态后在动载扰动下产生动力失稳造成冲击，因此从准静态系统的角度分析冲击地压并不能较好体现冲击地压产生时系统的动力特性。
荣海等[3]认为冲击地压是时空的统一并提出了煤岩动力系统失稳的概念，揭示了该系统空间结构与冲击地压显现的关系，从能量角度解释了冲击地压的动力失稳，但并未充分体现时间变化下各子系统间的联系；王来贵等[4]指出准静态平衡力学系统是岩石力学系统的一个特例或分支，由此进一步提出了运动稳定性的概念，认为岩石系统是一个动力系统，但运动稳定性并未分析动力系统中的惯性部分变化对系统性质的影响。时变力学方面，曹志远等[5]给出了黏弹性时变体损伤力学的基本方程，并对时变效应进行了定量分析；王华宁等[6]在分析地下岩石动态施工过程中的应力及位移变化时，认为岩石的黏性时效和外界扰动耦合作用引起应力和位移变化。马占国等[7]通过RFPA模拟出基于单元弱化原理的开采推进过程中产生的覆岩失稳破坏;王斌[8]通过质点系动量定理推出岩石系统与外界质量交换时时变系统的稳定性判据，但仅仅考虑了质量这一单一控制变量对系统的影响，并未对煤岩系统进行具体辨识。
综上所述，传统研究的不足主要在于准静态分析不能体现冲击地压的动力特性，涉及动力系统的研究大都忽略了时空演化过程中煤岩系统的动态变化；涉及时变力学的研究大都仅考虑了某种特定的时变情形，并未全面地分析时变系统特性的变化。冲击地压是煤岩系统某一个或多个参数变化进而诱发系统失稳的较为复杂的时变问题，因此笔者从动力系统的角度出发，结合时变力学原理提出了煤岩时变动力系统的概念，通过分析试件-试验机系统、煤柱顶板系统、巷道围岩系统的动力特性由一维到多维建立了广义的时变动力方程，针对不同情况进行了参数辨识，建立了时变动力系统的状态方程，对煤岩系统的时变特性进行讨论分析，并进一步分析其系统稳定性，为冲击地压的研究提供了一种新思路。
1 时变系统参数辨识
时变系统是指系统的特性随时间发生变化，系统的输入扰动和输出响应与其影响系统的时间起点有关，时变系统的可按时变因素分为两类：①系统内部的时变，即内部参数是时变的；②系统外部的不确定扰动(时间或来源不同)是时变的，以下讨论不同时变类型下的煤岩时变系统。
1.1 煤岩试件-试验机系统辨识
岩石力学可分为岩石静力学部分和岩石动力学部分，两部分的界限是不明确的，通常将应变率在1×10-1～1×104的载荷范围视为研究岩石动力学的最佳范围[9]，煤岩试件-试验机系统是研究煤岩的力学系统之一，由煤岩试样和动载试验机2个子系统构成，具备一些基本的力学性质，其系统模型如图1a所示。
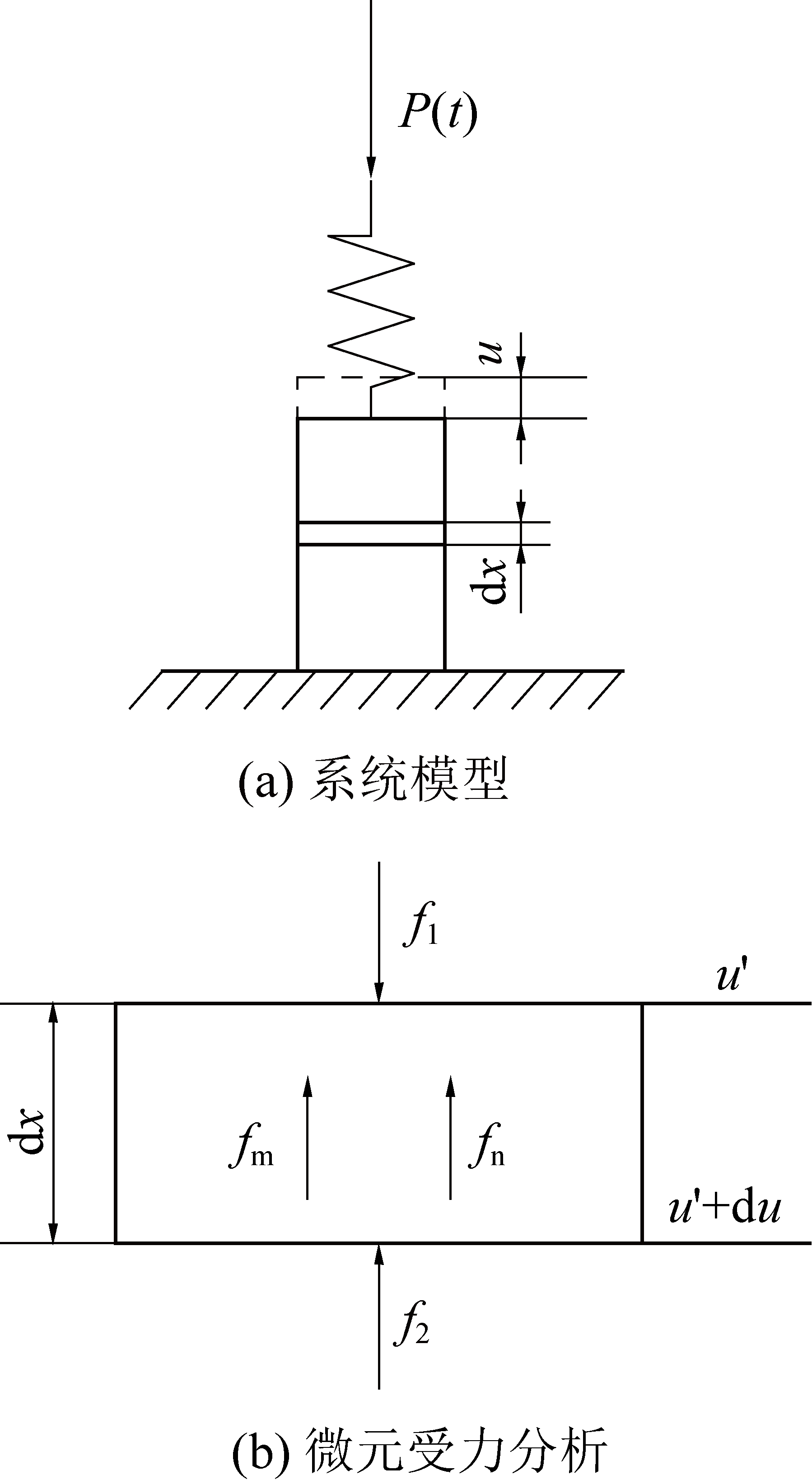
图1 煤岩试件-试验机系统
Fig.1 Coal rock specimen testing machine system
其中，煤岩试件变形为u=(s-a)，煤岩试件密度为ρ，试验机和煤岩试件总变形为s，试验机变形为a，试验机加载速度可控，荷载设定为与时间变量相关的线性函数P(t)。
图1b中，取厚度为dx、截面面积为As的微元进行分析，当试验机施加荷载较小时煤岩试件只发生弹性变形，试验机刚度表示为Ka，煤岩刚度表示为K，变形抵抗力fk、惯性力fm和阻尼力fn分别为
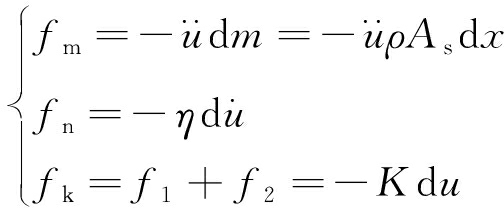
式中，
为试件阻尼系数；
为一阶导数，反映系统位移速度；
为二阶导数，反映系统加速度。
建立平衡方程，两端对x进行积分得：
(1)
对于煤岩试件试验机系统，扰动变量P(u,t)的时变会引起状态变量u以及控制变量ρ、η和K的时变，导致系统的特性发生改变，因此可视为时变系统，各变量如下：
系统状态变量由P(u,t)=Ka(s-u)两端对先后对t,x求导得：
煤岩具有应变软化的性质，因此在外载超过峰值载荷后刚度K会随着变形的时变而时变，对于阻尼项和惯性项如下式所示：
式中，h,m分别为煤岩试样的高度和质量。
综上所述，对于煤岩试件-试验机系统，系统由于外部扰动的时变而引起整个系统状态的变化，因此煤岩试件-实验机系统可视为一个外界扰动时变的能控时变系统。
1.2 顶板煤柱时变系统辨识
采矿工程中常采用在相邻采区或工作面之间预留煤柱的方法，顶板煤柱系统同样可视为一个一维系统，顶板煤柱系统受外界扰动影响较大，顶板传递的荷载往往受工程中复杂的施工情况影响，导致外界对系统的扰动P(t)也产生差异。如采空区顶板自由垮落引发的扰动由采空区长度决定，巷道扩修和充填开采对应的施工扰动形式亦不同，因此考虑此系统为一个扰动不可控的时变系统。在开采过程中，煤柱相邻采空区的顶板垮落会在煤柱中产生突然的应力集中，上覆岩层给予系统的外界扰动突然变化，此时可将煤柱视为一维动力系统，其简化模型如图2所示。
图2 顶板煤柱时变系统
Fig.2 Time varying system of roof pillar
其系统动力方程形式与式(1)相同，因此将顶板煤柱系统视为时变系统，令y=du/dt可得：
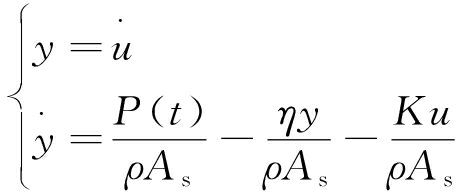
(2)
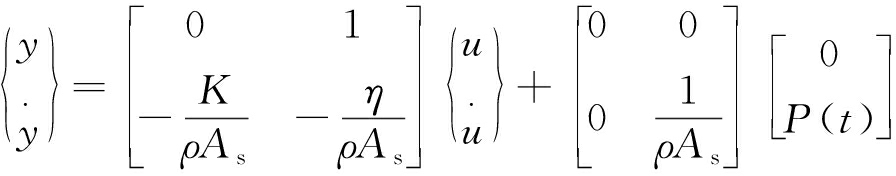
表示为系统状态方程的形式:
式中：A为系统状态矩阵;B为输入矩阵;X为状态矩阵;F为扰动矩阵。
外载时变下此系统状态空间方程矩阵皆为时变矩阵，可知顶板煤柱系统是一个扰动时变的不可控时变系统。
1.3 巷道围岩系统辨识
巷道开挖引起巷道围岩应力场的重分布，围岩应力由原来的三维应力平衡状态转变为二维平衡状态。在开挖过程中巷道围岩系统与外界存在质量交换，假定在巷道开挖时，碎石脱落的瞬间向水平方向运动，将巷道围岩问题简化为平面应变问题，可将巷道围岩系统简化为二维动力系统，如图3所示。
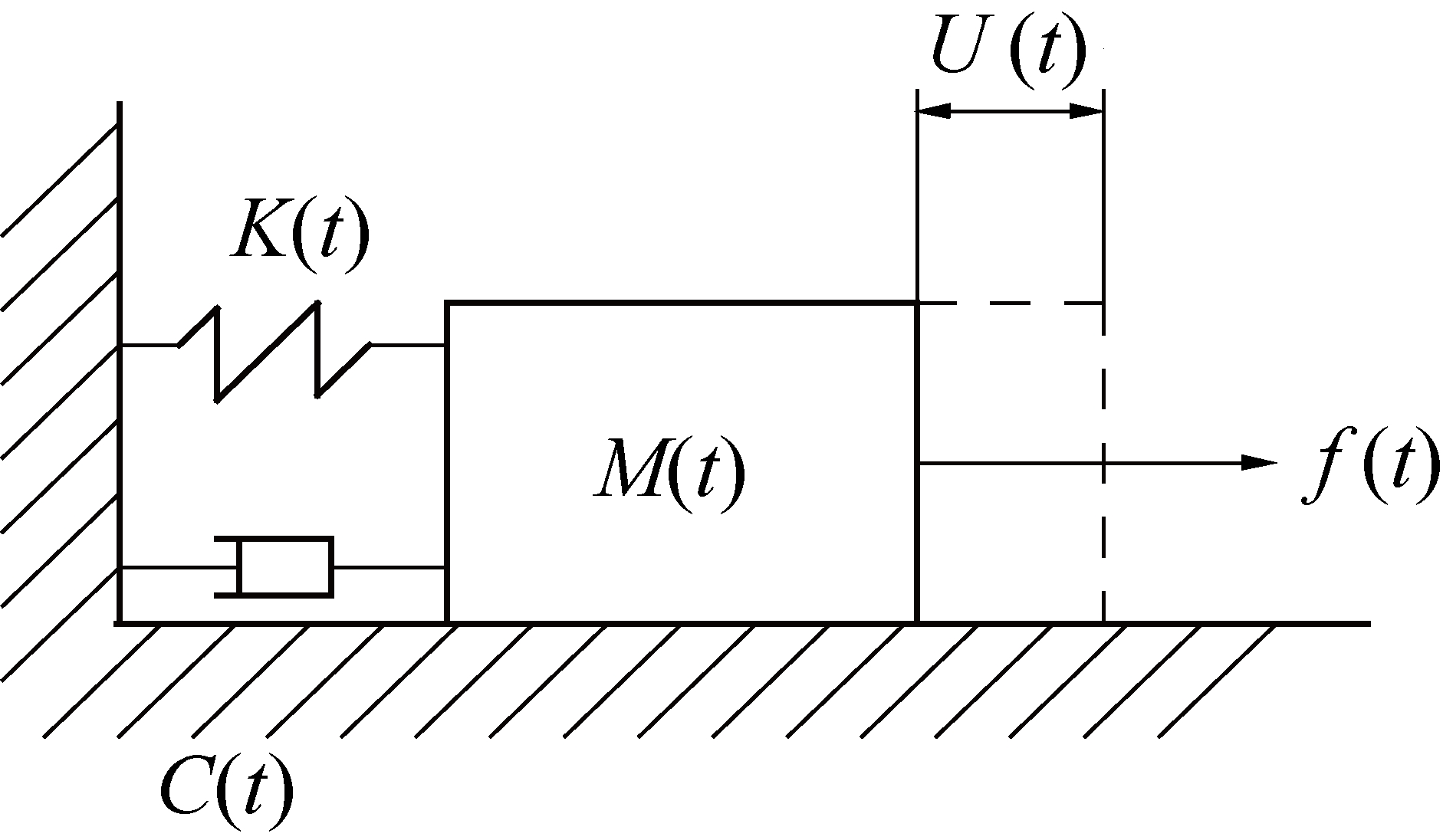
图3 巷道围岩时变系统
Fig.3 Time varying system of roadway surrounding rock
应力集中导致部分围岩体达到其峰值强度而产生塑性软化，在此过程中岩石内部裂缝发育扩展至产生宏观破裂，形成不连续面。进而可认为巷道围岩系统的质量为时变质量M(t)，刚度为时变刚度K(t)，系统阻尼为C(t)，围岩受到外部扰动f(t)时产生变形U(t)，根据图3可得巷道围岩系统的时变动力响应方程：
[K(t)]{U(t)}={f(t)}
(3)
将式(3)经过非奇异变换：
可将时变动力响应方程转换成时变系统状态空间方程[10]，如式(4)所示。
(4)
外部作用力往往通过对系统内部因素的作用对系统状态产生影响，因此时变系统输出方程的直接输出矩阵为零矩阵，其输出响应方程为
{Y(t)}=[D(t)]{X(t)}
(5)
式中，
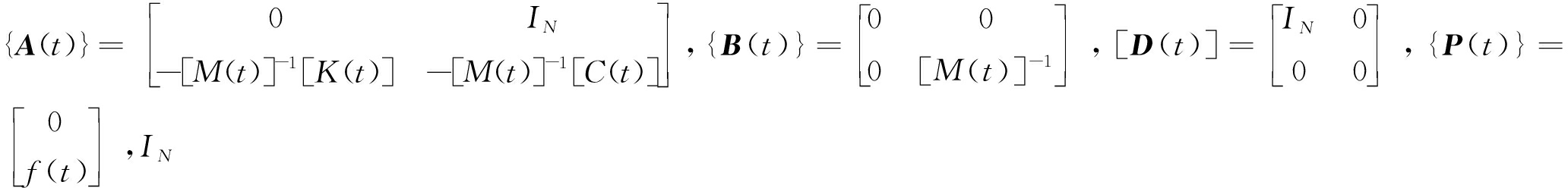为N阶方阵。
若考虑巷道围岩系统与外界的质量交换，即质量时变，令产生质量交换的微元质量为dM，质量为M(t)的巷道围岩系统在外部扰动f(t)作用下的速度响应为dU(t)/dt，由动量定理可得巷道围岩系统的时变动力方程[8]:
式中，r(t)为微元脱离系统的释放速度。
但微元脱离速度相对于系统整体运动速度可以忽略，上式可表示为
[K(t)]{U(t)}={f(t)}
(6)
当巷道开挖时巷道围岩系统质量减少，即dM(t)/dt 为负，随着巷道围岩的变形以及开挖引起质量时变，导致系统阻尼减小。式(6)中的阻尼部分反映系统的流变特性，说明质量时变的巷道围岩系统的流变特性会随着巷道施工而时变；当不考虑阻尼时，由于dM(t)/dt为负，巷道围岩系统等效于负阻尼系统，对系统的微小扰动将会一直放大，系统处于非稳定状态，此时巷道围岩系统在一定扰动下极易失稳破坏产生冲击地压。
2 煤岩时变系统特性分析
2.1 煤岩时变系统的线性分析
上文基于式(3)分别对扰动时变、质量时变和系统边界时变的顶板煤柱系统和巷道围岩系统进行了系统辨识和参数辨识，得到不同时变类型的时变系统参数的差异性，但无论对于哪种类型的时变系统，其时变系统的系统特性是一致的。对于巷道围岩系统来说，巷道围岩时变子系统的拆分为基于线性时变系统的叠加性得出的结论。线性系统的叠加性是指，系统在几个外界扰动的共同作用下产生的动力响应为几个扰动分别作用于系统所得响应的总和。假设两个外部扰动P1(t),P2(t)共同作用于式(4)描述的时变系统，其先运行系统后进行线性运算得：
相加得：
{X2(t)}]+[B(t)]{P1(t)+P2(t)}
先经线性运算后再运行系统：
[B(t)]-1[A(t)][{X1(t)}+{X2(t)}]
前后两式等价满足叠加性。若要证明煤岩系统为线性时变系统还必须满足均匀性，当外力f(t)作用于系统时产生响应Y(t),若令外力扰动增大N倍，先通过系统再线性运算则有：
N{Y(t)}=N[D(t)]{X(t)}
先经线性运算再经过系统得：
N{X(t)}=[D(t)]-1N{Y(t)}
显然满足均匀性，因此式(4)所表示的巷道围岩时变系统为线性时变系统，其系统状态方程的解[14]如式(7)。线性系统的一个重要性质是其系统的响应可分为非零初始状态X(t0)引起的振动响应和由于外力作用于系统产生的振动响应，对应于式(7)中的前后2项，分别反映地下岩石系统在初始时刻由于初始地应力作用产生的变化，以及在开采过程中由于外部扰动对岩石系统产生的影响，其中Φ(t,t0)为时变转移矩阵。
{X(t)}=Φ(t,t0){X(t0)}+
Φ(t,τ)[B(τ)]{P(τ)}dτ
(7)
2.2 煤岩时变系统的能控性与能观性分析
能控性和能观性是现代控制理论中系统的重要特性。能控性决定系统状态{X(t)}是否能在有限时间内，在外力{f(t)}的作用下达到任意的终状态则此系统能控。在地下开采过程中，能控性体现在选取合适的巷道布局和支撑方式改善围岩结构和赋存环境，进一步控制煤岩系统的变形和破坏，其本质为通过调整时变系统的控制变量如质量、阻尼和刚度来限制系统的状态变量变形、速度、加速度的变化，若能通过适当的方式将不能控的系统转变为能控的系统，也就实现了冲击地压的防治。
能观性反映了系统状态变化引起的系统响应变化，即在任意给定的外力{f(t)}影响下，在有限时间内通过对应的系统响应{Yi(t)}，确定惟一系统状态{Xi(t)}，现有的现场监测技术，其基本思想是在即时应力状态下，通过监测系统响应将其转换为信号来分析系统的状态。因此分析系统的能观性和能控性对于冲击地压防治和监测都具有重要意义。对于线性时变系统，其能控和能观的充要条件为对应的GRAM矩阵非奇异[15]：
WC(t0,t1)=
Φ(t,τ)[B(τ)]Φ(t,τ)T[B(τ)]Tdτ
(8)
WO(t0,t1)=Φ(t,τ)[D(τ)]Φ(t,τ)T[D(τ)]Tdτ
(9)
式(8)、式(9)分别为能控性和能观性的GRAM矩阵，计算该矩阵的奇异性需要对时变转移矩阵Φ(t,τ)进行计算，但式(4)所表示的系统矩阵A(t)与
不满足乘法可交换，同时采用级数近似法需要有解析解，因此常通过状态方程中的系统矩阵A(t)和输入矩阵B(t)判断系统能控性。
Qc(t)≡(B1(t),B2(t),…,Bn(t))
式中，Qc(t)为能控性判别矩阵。
若存在某一时刻tf，使得rankQc(tf)=n，则此系统能控，通过式(4)得到Qc(tf)为
对于一维的煤岩试件-试验机系统(n=2)，此系统是状态完全能控的，即系统能控。通过类似的方法得到能观性判别条件可知此时变动力系统也是状态完全能观的。
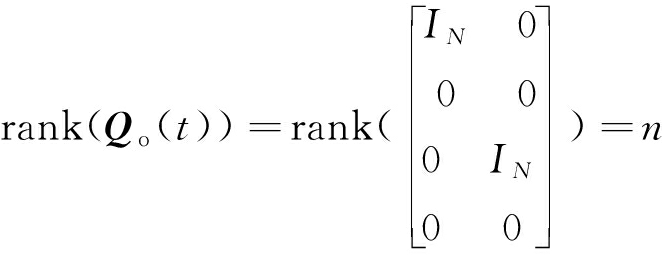
式中，Qo(t)为能观性判别矩阵。
综前所述，式(3)所示的煤岩时变动力系统是能控和能观的，因此能通过调整合理的采场布局选取系统控制变量M(t),C(t),K(t)，使得系统状态维持在一个稳定的程度，进而达到防治冲击地压的目的。
3 煤岩系统的时变动力响应分析
3.1 巷道围岩系统边界时变稳定性分析
在上述几种时变过程中，往往伴随系统边界的变化，称为边界时变问题。以巷道围岩系统为例，巷道掘进过程中部分块体脱落引起质量时变，由于围岩应力的变化，巷道围岩演化出新的弹性区、破裂区和塑性软化区，诸多学者基于弹塑性理论和破裂条件给定了静态巷道围岩系统塑性软化区和破裂区的范围[11-13]。
但在动态施工扰动下，不同分区范围亦是时变的，即不同子系统的边界是时变的，这类边界时变问题同时伴随着子系统间的质量、阻尼和刚度变化，以圆形巷道质量时变为例，如图4所示。塑性区和破裂区半径由于边界时变分别由R1,R2发展至R1+dR1,R2+dR2，进而得到弹性区和塑性区、塑性区和破裂区之间的质量变化dM(t)为
图4 围岩分区边界时变示意
Fig.4 Time varying of surrounding rock zoning boundary
将3个状态区域视为3个子系统，对于塑性软化系统若不考虑阻尼影响，由式(6)可得，当dM1(t)>dM2(t)时系统等效于负阻尼系统，当dM1(t)>dM2(t)时，随着不同子系统边界的时变，等效于阻尼增长的时变系统，系统的稳定程度增加。若考虑系统阻尼，可得塑性区系统的稳定程度变化规律为
1)当
时，系统稳定度增加，塑性区等效于阻力区的作用。
2)当
时，系统稳定度降低，塑性区半径随边界时变发展至一定程度时系统等效于负阻尼系统，此过程是巷道围岩系统由稳定结构转换为非稳定结构的过程。对于破裂区子系统上述方法同样适用。
3.2 煤岩时变系统一般稳定性理论
目前对于煤岩系统稳定性的分析大都基于运动稳定性理论[16]，但运动稳定性理论并不考虑质量和边界的变化问题；此外还存在输出稳定性，即外部产生有界的扰动引发发散的响应，潘一山[17]的扰动响应理论给出非稳定系统有界扰动引发无界响应的判别准则，尹祥础等[18]的非线性系统响应比理论也给出系统产生输出失稳的判定准则。目前时变系统的稳定性理论研究是基于李雅普诺夫稳定性理论开展的，由李雅普诺夫第1法可知线性时变系统稳定的充要条件为系统矩阵A(t)的所有特征值均有负实部，系统状态矩阵的质量阵M(t)正定，所以线性时变系统失稳的等价条件为存在负定的刚度阵K(t)或阻尼阵C(t)。
由李雅普诺夫第2法对系统稳定性进行判定，由系统状态方程式(4)选取连续对称正定矩阵Q(t)，此时必然存在一个连续对称正定矩阵P(t)，满足：
(10)
并可由此构造反映系统能量的函数：
V(X,t)={X(t)}T[P(t)]{X(t)}T
当P(t)满足方程(10)时正定，d[V(X,t)]/dt为负定的，此系统处于稳定平衡状态，若d[V(X,t)]/dt为半负定，可由李雅普诺夫辅助判据[19]得到系统稳定性条件，当d[V(X,t)]/dt正定时，煤岩时变系统为非稳定状态，煤岩变形能不断积累，累积到一定程度能量释放产生冲击地压。但由于李雅普诺夫方程很难得到解析解，只能通过离散化原理转换成离散时变系统或基于冻结系数法考虑时变系统的瞬时状态将其转换为时不变系统，并通过Matlab计算数值解。
3.3 案例分析
以某矿7121孤岛工作面的模型为例[20]，取g=9.81 m/s，煤体密度为1 400 kg/m3，厚度为3 m，体积模量和剪切模量分别为1.7 GPa和0.8 GPa，计算得泊松比μ=0.297，煤岩弹性模量K为2.1 GPa，上覆岩层及顶板传递荷载为16 MPa，顶板泥岩弹性模量Ka为3.79 GPa。为简化计算，系统阻尼按瑞利阻尼C=a*[M]+b*[K]计算，a,b为瑞利阻尼系统，考虑煤岩性质a=0.02,b=10-6，并给予系统简谐振动形式的开采扰动，分别应用李雅普诺夫第1法和李雅普诺夫第2法分析系统稳定性。
在开采扰动下，煤岩时变系统中的位移响应变化如图5a所示，煤岩时变系统中煤柱变形速度du/dt的变化情况如图5b所示，由图5可以看出施工扰动下系统变形和速度响应会在系统内随时间呈现衰减振动的趋势，即扰动响应比dp/dy不为0，此时系统时变引起的稳定度变化并未使系统失稳，此状态下反应系统能量的李雅普诺夫函数的一阶导数为负定，李雅普诺夫函数为半正定的，且系统状态矩阵的特征值具有负实部，以上均符合李雅普诺夫第1法和第2法对稳定系统的描述。
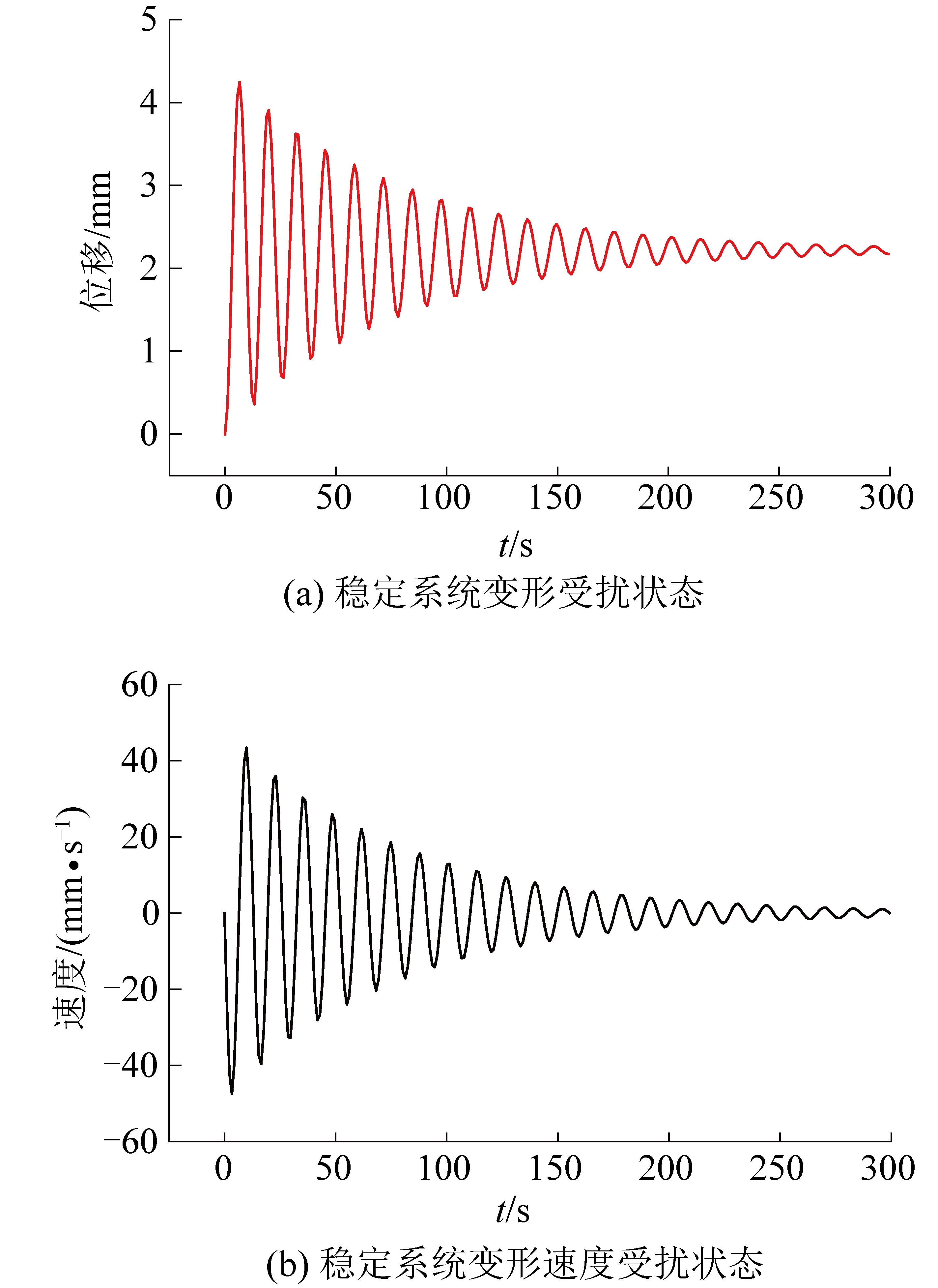
图5 稳定顶板煤柱时变系统受扰状态演化
Fig.5 Disturbed state evolution of stable
roof coal pillar time varying system
但对于一般的采矿工程过程中，随着开采的进行，煤岩系统状态继续发生改变，在特定条件下可由稳定系统发展至非稳定的强冲击倾向性系统，例如在巷道扩修至某一时刻，煤岩系统由于系统内外质量交换及煤岩应变软化使系统等效于负阻尼系统时，此时取瑞利负阻尼参数a=-0.02,b=-10-6，此时煤岩时变系统是不稳定的，此时若给予系统微小的开采扰动，系统就会产生负阻尼振动。
图6 非稳定顶板煤柱系统受扰状态演化
Fig.6 Disturbed state evolution of coal
pillar system with unstable roof
图6a、6b分别为煤岩时变系统变形和变形速度，可知煤岩时变系统在微小扰动作用下系统振动将不断放大至系统失稳，此时扰动响应比dp/dy=0，在一定扰动下煤柱顶板时变系统失稳诱发冲击地压，此时系统状态矩阵特征值均不具有负实部，不符合李雅普诺夫第1判据，能量函数及其导数都为半负(正)定，也不适用于李雅普诺夫判据。但此判据仅为稳定系统的充分条件，并不能因此判断此系统为非稳定系统，应当结合式(6)得到等效于负阻尼的非稳定系统的质量阻尼失稳判别准则，判断系统的稳定状态，此为系统失稳的必要条件。
此外李雅普诺夫稳定性理论讨论的是无穷时间区间上的系统稳定性，但在地下开采过程中，我们仅需保障煤岩系统使用期间的稳定，因此可根据此情况采用有限时间的时变系统稳定性分析。有限时间下系统稳定性分析可分为2种方法：一是构造V型函数,由此WEISS[21]给出了有限区间内一般非线性时变系统稳定的充要条件。二是基于系统所有轨线包线求得系统稳定的充要条件[22]。
综上可知，采用时变力学原理从时变系统的角度分析煤岩系统稳定性与传统的稳定性理论有共通之处，但考虑了系统的时变特性更能体现煤岩系统在工程中由于动态施工等因素的影响产生的变化。例如巷道开挖、扩修或工作面掘进的过程中系统存在质量时变，同时伴随着边界时变问题，巷道围岩系统在扩修过程中由于上述原因系统稳定程度不断下降，当达到特定条件时煤岩系统在扰动下失稳产生冲击地压。此外煤岩产生应变软化时，式(3)中的刚度矩阵为时变的，随着时变的演化系统稳定度降低，当刚度矩阵为负定时，系统亦会由稳定结构变为不稳定结构。
4 结 论
1)从动力系统的角度出发，分别论证了煤岩试件-试验机系统、顶板煤柱系统和巷道围岩系统的时变特性，得到了扰动和质量等不同时变类型影响下的系统变化规律，证明了冲击地压是一个煤岩系统时变问题，进一步得到弹性区、塑性区和破裂区3个子系统的稳定度演化规律，得到了煤岩系统失稳的简单判据，建立了统一的时变动力系统方程。
2)构建了煤岩时变动力系统的简化模型，从叠加性、均匀性、能控性和能观性分析了煤岩时变动力系统的特点，采用李雅普诺夫稳定性理论分析了此线性时变系统的稳定性，并初步讨论了冲击地压与煤岩时变系统的联系，验证了时变力学原理分析冲击地压的合理性。
3)应用李雅普诺夫第1和第2判据从系统状态及能量角度得到冲击地压发生的充分条件，并利用冻结系数法初步验证了该判据的可靠性。初步探究了控制变量和扰动变量时变对系统稳定程度的影响，为冲击地压的研究提供了一种新的思路，但对于地下岩土工程来说，线性时变系统只是煤岩非线性时变系统中的一个特例，需要后续研究更具有工程实际的非线性时变系统模型。
[1] 姜耀东, 潘一山, 姜福兴, 等. 我国煤炭开采中的冲击地压机理和防治[J]. 煤炭学报, 2014, 39(2):205-213.
JIANG Yaodong, PAN Yishan, JIANG Fuxing, et al. Mechanism and prevention of rock burst in coal mining in China [J].Journal of China Coal Society, 2014, 39(2): 205-213.
[2] 潘俊锋,宁 宇,毛德兵,等.煤矿开采冲击地压启动理论[J].岩石力学与工程学报,2012,31(3):586-596.
PAN Junfeng, NING Yu, MAO Debing, et al. Initiation theory of rock burst in coal mining [J].Chinese Journal of Mechanics and Engineering, 2012,31(3): 586-596.
[3] 荣 海,张宏伟,梁 冰,等.煤岩动力系统失稳机理[J].煤炭学报,2017,42(7):1663-1671.
RONG Hai, ZHANG Hongwei, LIANG Bing,et al. Instability mechanism of coal rock dynamic system [J]. Journal of China Coal Society, 2017,42(7): 1663-1671.
[4] 王来贵, 黄润秋. 岩石力学系统运动稳定性理论及其应用[M]. 武汉:地质出版社, 1998.
[5] 曹志远,王华宁.粘弹性时变体的损伤演化理论与分析[J].固体力学学报,2004(2):159-164.
CAO Zhiyuan, WANG Huaning. Damage evolution theoryand analysis of viscoelastic time variant [J]. Acta Mech Solid Sin, 2004(2): 159-164.
[6] 王华宁, 曹志远. 圆形洞室动态施工中围岩粘弹时变解析分析[J]. 同济大学学报(自然科学版), 2008, 36(1):17-21.
WANG Huaning, CAO Zhiyuan. Viscoelastic time-varying analysis of surrounding rock in dynamic construction of circular cavern [J]. Journal of Tongji University(Natural Science Edition), 2008, 36(1): 17-21.
[7] 马占国, 黄 伟, 郭广礼,等. 覆岩失稳破坏的时变边界力学分析[J]. 辽宁工程技术大学学报, 2006, 25(4):515-517.
MA Zhanguo, HUANG Wei, GUO Guangli, et al. Time dependent boundary mechanical analysis of overburden failure [J]. Journal Of Liaoning Technical University Natural Science, 2006, 25(4): 515-517.
[8] 王 斌. 冲击地压发生机制的时变动力学分析[J]. 矿业工程研究, 2009, 24(1):1-6.
WANG Bin. Time varying dynamic analysis of rockburst mechanism [J]. Mining Engineering Research, 2009, 24(1): 1-6.
[9] 黄理兴.岩石动力学研究成就与趋势[J].岩土力学,2011,32(10):2889-2900.
HUANG Lixing. Achievements and trends of rock dynamics [J]. Rock and Soil Mechanics, 2011,32(10): 2889-2900.
[10] 曹志远, 邹贵平, 唐寿高. 时变动力学的Legendre级数解[J]. 固体力学学报, 2000, 21(2):102-108.
CAO Zhiyuan, ZOU Guiping, TANG Shougao. Legendre series solution of time-varying dynamics [J].Acta Mech Solid Sin, 2000, 21(2): 102-108.
[11] 蒋斌松,张 强,贺永年,等.深部圆形巷道破裂围岩的弹塑性分析[J].岩石力学与工程学报,2007(5):982-986.
JIANG Binsong, ZHANG Qiang, HE Yongnian,et al. Elastopla-stic analysis of broken surrounding rock of deep circular roadway [J].Chinese Journal of Mechanics and Engineering, 2007(5): 982-986.
[12] 高 强. 深部巷道分区破裂动力分析及支护研究[D].济南:山东大学,2019.
[13] 陈 梁,茅献彪,李 明,等.基于Drucker-Prager准则的深部巷道破裂围岩弹塑性分析[J].煤炭学报,2017,42(2):484-491.
CHEN Liang, MAO Xianbiao, LI Ming,et al. Elastoplastic analysis of surrounding rock of deep roadway fracture based on Drucker Prager criterion [J].Journal of China Coal Society, 2017,42(2): 484-491.
[14] 刘 豹, 唐万生. 现代控制理论[M]. 北京:机械工业出版社, 2006.
[15] 郑大钟. 线性系统理论.第2版[M]. 北京:清华大学出版社, 2002.
[16] 王来贵,刘向峰,宁民霞,等.岩石力学系统演化过程研究现状[J].辽宁工程技术大学学报,2002(5):590-594.
WANG Laigui, LIU Xiangfeng, NING Minxia,et al. Research status of rock mechanical system evolution process [J].Journal of Liaoning Technical University Natural Science, 2002(5): 590-594.
[17] 潘一山.煤矿冲击地压扰动响应失稳理论及应用[J].煤炭学报,2018,43(8):2091-2098.
PAN Yishan. Instability theory and application of coal mine rockburst disturbance response [J].Journal of China Coal Society, 2018,43(8): 2091-2098.
[18] 尹祥础,尹 灿.非线性系统失稳的前兆与地震预报:响应比理论及其应用[J].中国科学(B辑化学生命科学地学),1991(5):512-518.
YIN Xiangchu, YIN Can. Precursors and earthquake prediction of nonlinear system instability: response ratio theory and its application [J]. Science of China(SERIES B, geology of chemical Life Sciences), 1991(5): 512-518.
[19] LYAPUNOV A M. The general problem of the stability of motion[J]. International Journal of Control, 1992, 55(3):531-534.
[20] 桑鹏程,王 彪.千米深井孤岛煤柱工作面沿空掘巷冲击地压控制技术研究[J].煤炭工程,2017,49(9):101-104，109.
SANG Pengcheng, WANG Biao. Study on rock burst controltechnology of driving along goaf in isolated island coal pillar working face of kilometer deep mine [J]. Coal Engineering, 2017, 49(9): 101-104，109.
[21] WEISSL. Converse theorems for finite time stability[J]. SIAM
Journal on Applied Mathematics, 1968, 16(6):1319-1324.
[22] GARCIA G, TARBOURIECH S, BERNUSSOU J. Finite-time stabilization of linear time-varying continuous systems[J]. IEEE Transactions on Automatic Control, 2009, 54(2):364-369.
