0 引 言
钻井井壁竖向稳定性是煤矿深立井建井中的技术难题，也是钻井法应用与推广中的瓶颈，深入研究井壁结构竖向稳定性对提升钻井法凿井技术的理论基础和工程应用具有重大意义。多年来相关学者从不同的角度对该问题进行了大量研究，其中最具代表性的理论有弹性力学、结构稳定理论及能量法。文献[1-2]最早提出该问题，并将井壁视为一个两端铰支的细长杆，假定井壁截面等刚度且井筒内注满配重水，建立了等断面满水钻井井壁竖向稳定临界深度计算公式，为后续研究奠定了良好的研究基础。文献[3]也将配重水视为自重，基于井壁断面连续变化的假定，建立了变断面钻井井壁结构在满水和非满水情况下的临界深度计算公式，其结论同采矿设计手册[4]。文献[5-6]将内侧配重水压力和外侧泥浆的压力视为侧向均布荷载，分别建立了等断面满水和非满水钻井井壁结构竖向稳定临界深度计算公式；文献[7-8]用外推法进一步建立了变断面钻井井壁竖向稳定临界深度计算公式，并首次采用ABAQUS数值模拟计算方法验证了理论解；文献[9-10]将井壁结构视为上端自由、下端固定的压杆，分别考虑井壁自重和泥浆浮力作用，建立了临界深度计算公式；文献[11-12]通过稳定系数判定钻井井壁稳定性的各项影响因素，并考虑了由于测量误差和井壁的收缩变形造成的初始缺陷对井壁竖向稳定性的影响。上述理论研究通过建立不同的力学模型由能量法确立了井壁临界深度，在一定程度上解释了井壁竖向失稳的力学机制。但研究方法较集中且单一，工程实际推广力度不够，解决工程实际问题还需要做一定的工作。因此，对于钻井井壁竖向失稳机理仍需开展深入的研究。
随着现代数学理论的发展，非线性理论和突变理论也被应用到岩体系统失稳领域，尤其是煤岩体系统的失稳分析。基于钻井井壁悬浮下沉至井底后失稳的突变性和不可逆性的特征，提出采用突变理论分析井壁竖向失稳的力学机理，尝试从突变模型失稳控制的角度对井壁结构稳定进行监控和有效防治，为钻井井壁结构竖向稳定性的理论研究提供一种新的定量分析方法。
1 突变理论及其应用
1972年法国数学家THOM运用分叉理论、奇异性、拓扑学等数学工具提出的突变理论，强调系统的非线性、不可逆性及突发性，解释了各种形态、结构的非连续性突变现象，研究了系统从一种稳定组态跃迁到另一种稳定组态的现象和规律[13-15]。基于此，穆成林等[16]基于巷道顶部围岩受力的非线性和突变特征，给出了巷道层状围岩的失稳机制及判据。文献[17-18]采用突变理论研究了露天矿边坡开挖稳定性问题。文献[19-22]利用尖点突变模型分析了采空区矿柱-护顶层支撑体系的破坏机制，给出了支撑体系的失稳准则。均取得了良好的研究效果。
钻井井壁在漂浮下沉过程中的竖向失稳破坏是一个由渐变到突变的演化过程，随着井壁结构的不断接长和井筒内注入的配重水不断增多，井壁结构开始积聚弹性能，且井壁结构系统积累的总势能保持的稳定平衡具有动态和不确定性。当系统弹性势能积聚到一定程度时，处于动态平衡状态的井壁结构在外界扰动的作用下就会诱发结构失稳，只要有微小的偏心或横向力都会使井壁突然倾斜、滑移，进而造成井壁结构竖向失稳，且具有明显的突发性，破坏后不可逆。因此，突变理论也可用于分析钻井井壁结构竖向稳定性问题。
突变理论通过给出系统在突变过程的势能函数，讨论相应的突变模型，特别是控制空间中突变集的几何形状，应用于不连续现象的定性和定量研究。托姆分类定理进一步指出，对于控制空间不超过四维、状态空间不超过二维的系统，只有7种基本灾变形式。其中只有2个控制变量和1个状态变量的尖点灾变形式最为常见。其势函数的标准形式是
(1)
其中：x为状态变量，m、n为控制变量。令势函数Π(x)一阶导数为0，即
Π′(x)=x3+mx+n=0
(2)
使势函数的导数值为0的点就是最简单的奇点，或称为临界点。所有的临界点所组成的曲面则为平衡曲面M。而临界点不一定是稳定点，临界点可能使系统稳定或不稳定。只有使势函数取惟一极值的点才是稳定点，因此要想使系统稳定，还需要同时满足方程
Π″(x)=3x2+m=0
(3)
联立式(2)和式(3)，得到分叉集方程式(4)。满足方程(4)的点组成了奇点集S。S在控制空间C中的投影B称为分歧点集B。
Δ=4m3+27n2=0
(4)
图1绘出了尖点突变模型的平衡曲面M及分歧点集B，其中平衡曲面M是一个由状态变量x，控制变量m、n组成的流行曲面。且临界点x可以看作m、n的单值或多值函数，记作x=f(m,n)。这是一个有光滑折痕的曲面，其上每一点代表所研究系统的一种平衡状态，且该平衡曲面被分成了上、中、下3叶。下叶是弹性势能增加失稳孕育的阶段，中叶为突变不稳定状态，上叶为失稳后的新稳定态[13]。
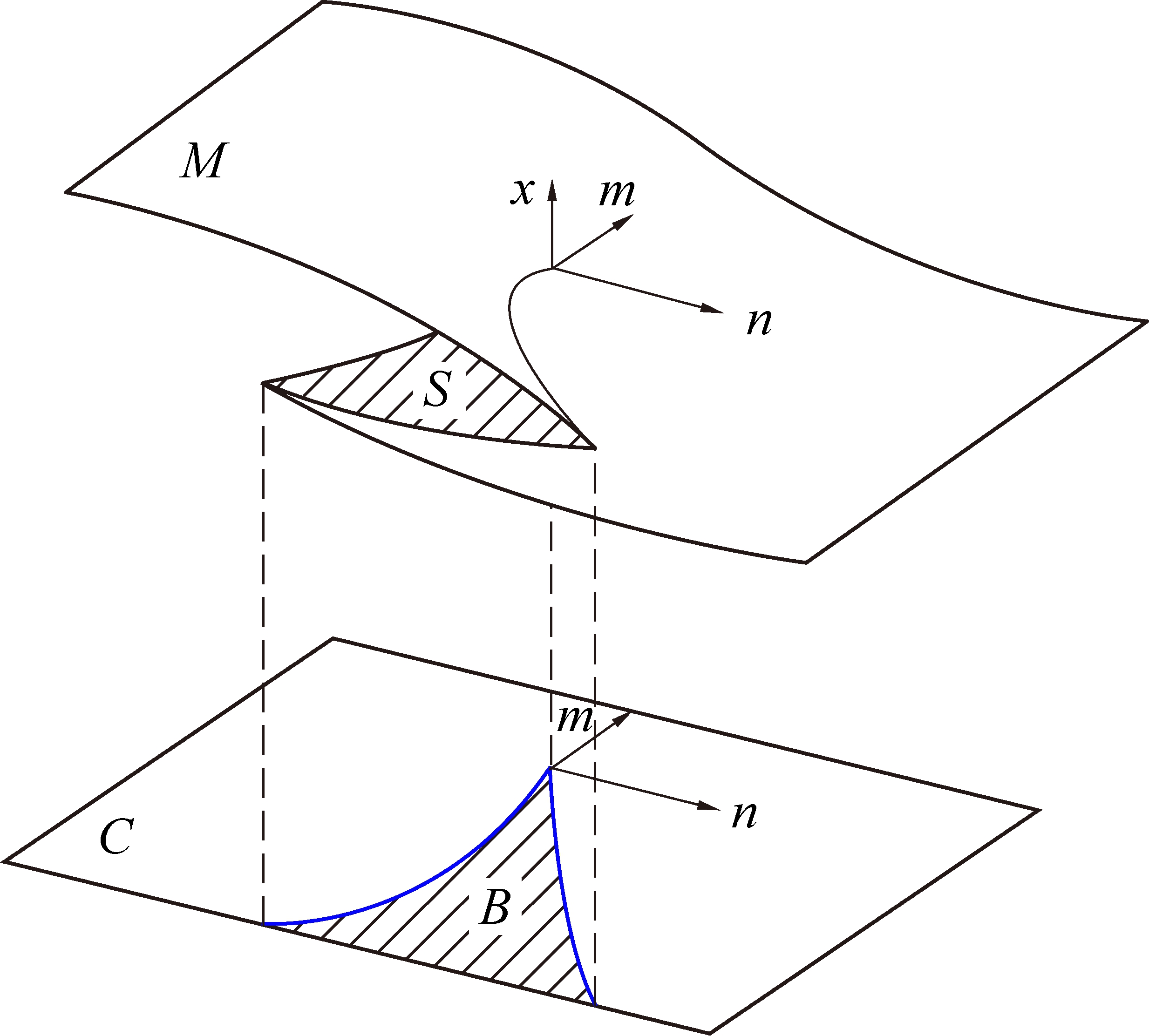
图1 尖点突变模型平衡曲面及分叉集示意
Fig.1 Diagram of equilibrium surface and bifurcation set
of cusp catastrophe model
2 钻井井壁竖向失稳突变模型
2.1 基本假定及力学模型
为方便，这里只讨论等断面钻井井壁的竖向稳定问题，并做如下基本假定：
1)井壁材料线弹性，且服从虎克定律。
2)井壁结构可视为两端铰支的细长杆，其挠曲线方程为
其中δ 为挠曲线中点最大位移，H为杆长。
3)井壁结构服从结构稳定小挠度理论，杆件无初始缺陷和初应力，屈曲时杆件只发生平面弯曲变形，且弯曲变形是微小的，满足
其中，EI为杆件截面刚度。
4)井壁与泥浆间无摩擦力和黏聚力。
在井壁悬浮下沉至井壁底但尚未进行壁后充填时井壁结构受力包括：井壁自重Pc、泥浆对井壁外表面作用的侧向压力Pm、配重水的重力Pw、井口支反力RB、井壁底反力RA，假设此时井筒内注满配重水，其受力分析情况如图2所示。单位长度泥浆对井壁外表面作用的侧向压力为pmsin α，其中
其受力方向沿着挠曲线的法线方向，α为挠曲线倾角；单位长度钢筋混凝土井壁自重为
单位长度配重水的自重为
其中，D为井筒外直径;d为井筒内直径;γc、γs,γm,γw分别为混凝土、钢筋、泥浆和配重水的容重；ρ为配筋率。由于支座A、B处未产生位移，故由RA、RB产生的外力势能为0。
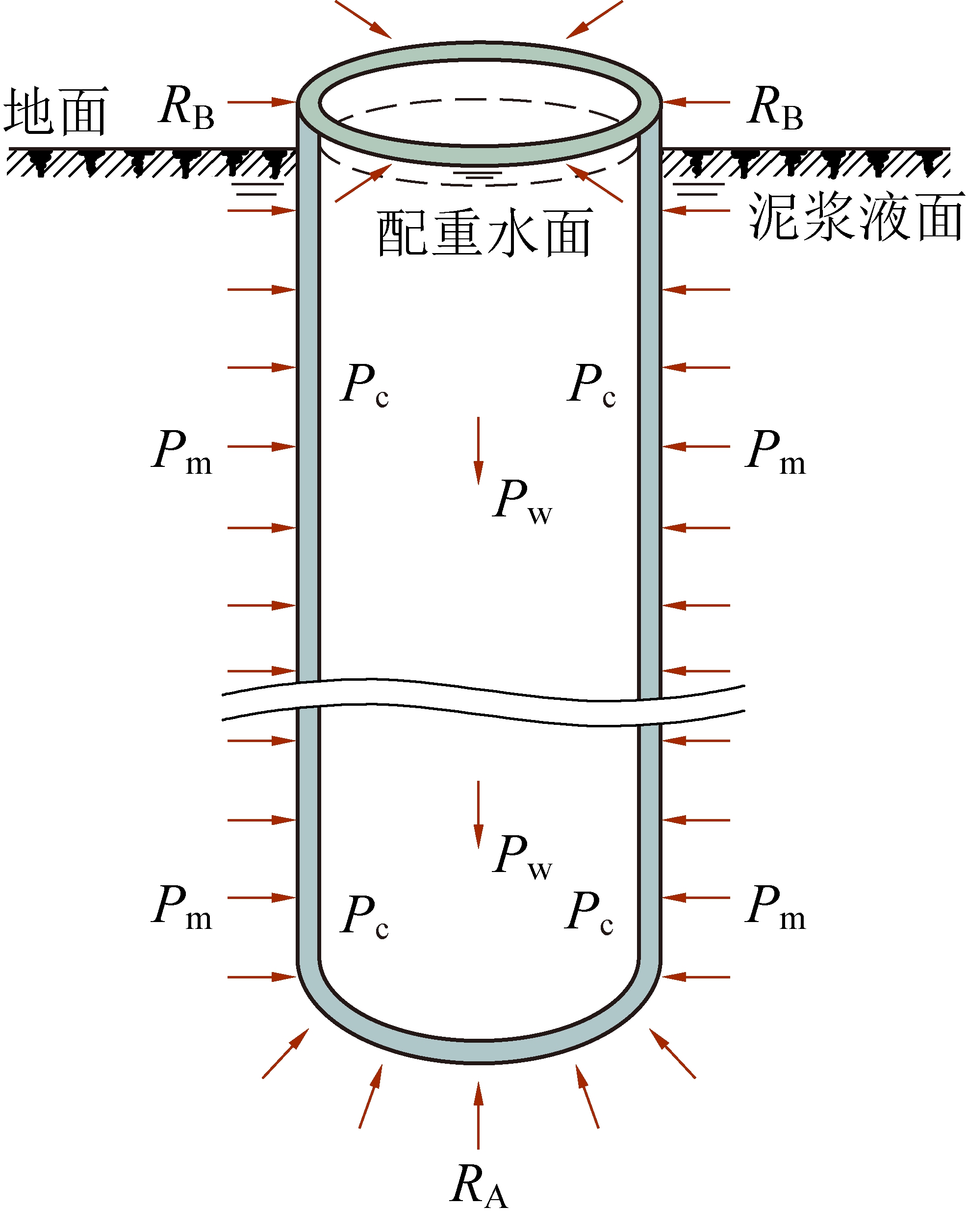
图2 悬浮下沉井壁受力分析
Fig.2 Mechanism analysis of shaft lining during sinking
由基本假定2及上述的受力分析，可得等断面钻井井壁变形挠度曲线及稳定性分析计算简图如图3所示。
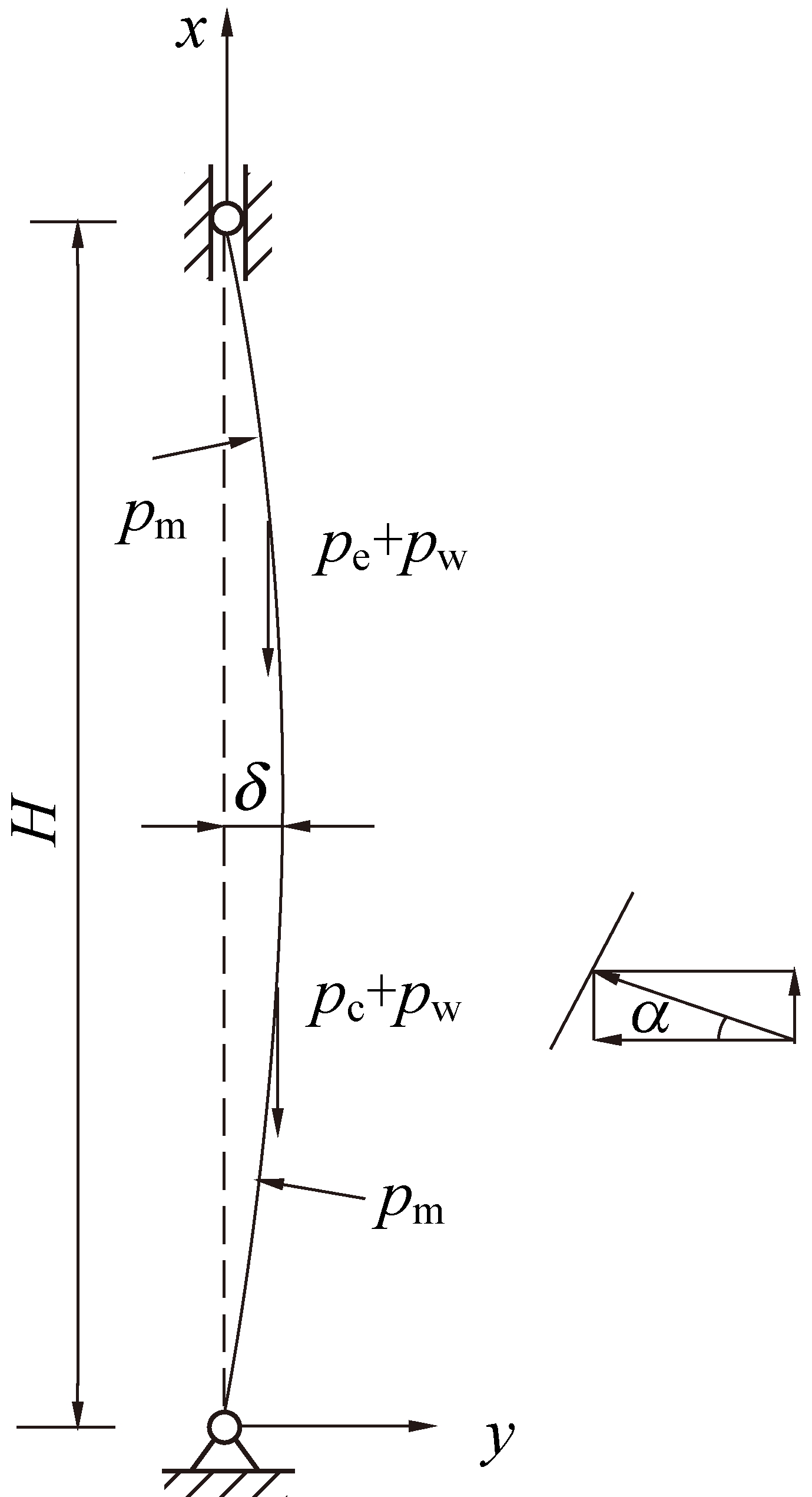
图3 井壁稳定性分析
Fig.3 Analysis of shaft lining stability
2.2 系统总势能函数
钻井井壁结构的总势能Π为结构竖向挠曲变形释放的应变能U与外力势能V之和，系统总势能函数可表示为
Π=U+V
(5)
由材料力学[23]及基本假定3可知，系统的应变能为
(6)
系统外力势能中由竖向力P引起的外力势能，可由Vy=-Pλ求得，其中λ为系统在竖向力作用下产生的微小形变，且形变量
而水平方向力引起的外力势能为水平方向力Q与位移δ的乘积，即Vx=Qδ，则系统的总外力势能为竖向力引起的外力势能与水平力引起的外力势能之和，因此，系统外力势能可进一步表示为
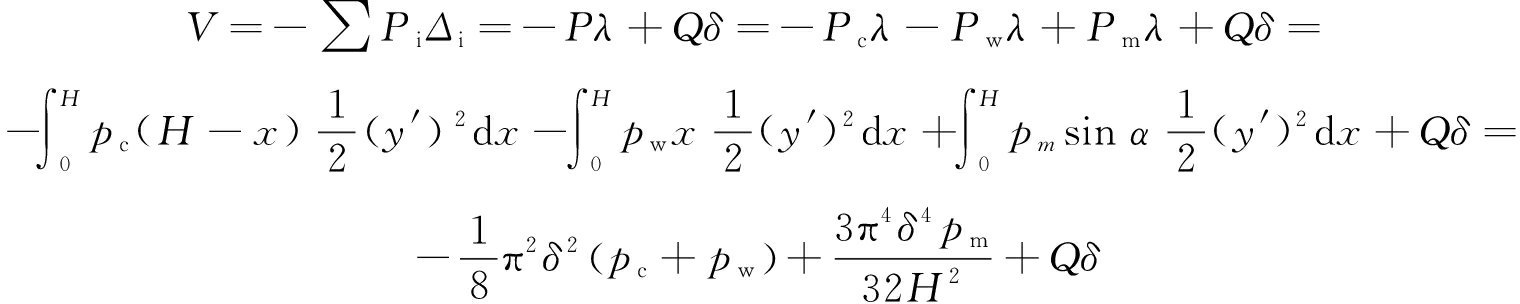
(7)
此时，系统的总势能为
(8)
2.3 井壁失稳突变模型
对式(8)做等量变换，令
(9)
(10)
A1=Q
(11)
同时，引入无量纲参数x，m，n，有
(12)
(13)
(14)
则系统总势能函数可表示为
(15)
该式有2个控制变量m、n，1个状态变量x，根据托姆分类定理等断面钻井井壁结构符合尖点突变数学模型。
3 井壁结构突变失稳机制分析及临界深度参数设计
3.1 突变失稳机制分析
在钻井井壁稳定性分析中，一般将建井过程划分为3个阶段，即悬浮下沉阶段、悬浮下沉至井底但尚未固井充填阶段、固井充填阶段。其中悬浮下沉阶段和固井充填阶段的井壁结构是稳定平衡的[2]，悬浮下沉至井底后至壁后充填前井壁结构处于随遇稳定平衡状态。因此，可以认为悬浮下沉阶段的钻井井壁位于图2中平衡曲面M的下叶；固井充填阶段的钻井井壁位于平衡曲面M的上叶，而悬浮下沉至孔底但尚未固井充填阶段的钻井井壁位于平衡曲面的中叶。
在突变理论中，控制变量m,n的取值直接决定系统的稳定状态。当且仅当系统的平衡点跨越分叉集时，系统才有发生竖向失稳的可能。而由控制变量组成的分叉集方程则是判定系统失稳的关键。当Δ>0时，控制变量(m,n)落在分歧点集B外部，系统位于平衡曲面的上叶和下叶，井壁结构处于稳定平衡状态。当Δ<0时，控制变量(m,n)落在分歧点集B内部，系统位于平衡曲面的中叶，井壁结构处于不稳定平衡状态。当Δ=0时，控制变量(m,n)落在分歧点集B的边界上，井壁结构处于临界稳定平衡状态。
这里
(16)
则
(17)
若Δ>0，井壁结构处于不稳定平衡状态；若Δ<0，井壁结构处于稳定平衡状态；当Δ=0时，井壁结构处于临界状态。
3.2 临界深度参数设计
当结构处于临界状态时，
则
则等断面满水状态下的钻井井壁竖向稳定临界深度为
(18)
此结论与《采矿设计手册》(中册)等断面井壁临界深度计算公式完全相同[4]。
在井壁施工中，配重水是控制井壁结构竖向稳定性的重要因素，在实际工程中有时并不需要加满配重水[24]，若在井筒内注入的配重水最大高度为Hw，则配重水做的外力功为
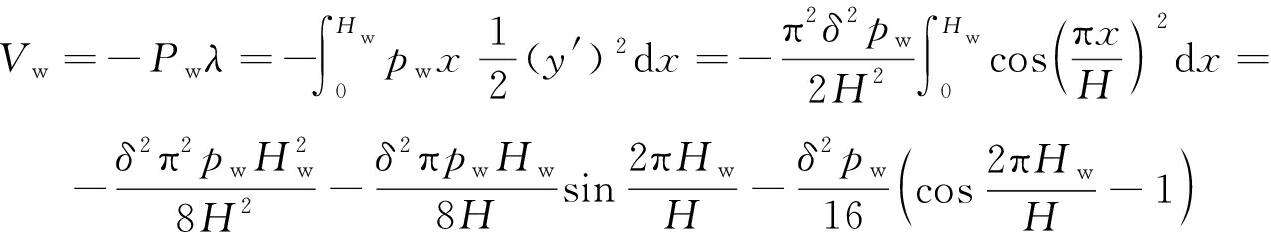
(19)
此时的势能函数为
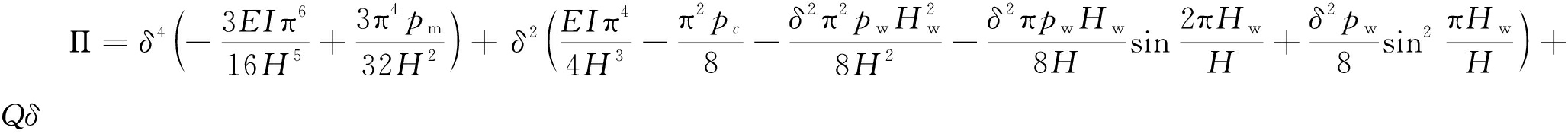
(20)
当井壁结构处于临界稳定状态时，由Δ=0判得非满水状态下井壁失稳临界深度为
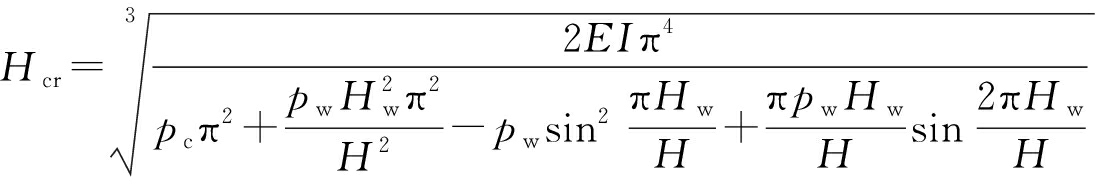
(21)
且在上式中，当H=Hw时，其结果同式(18),说明式(21)更具有一般性。
4 基于Python语言的突变失稳分析流程
利用突变理论得出的钻井井壁失稳机制及临界深度计算公式能有效指导钻井法施工，合理控制井壁结构的稳定性，防止或避免井壁倾斜、滑移，侧向位移突然增大，提供监测预报或提出有效的防治措施。既可以对已有的井壁结构和井型参数(如井壁深度、井壁厚度、配重水高度、截面刚度等)做稳定性判定，也可以对即将施工的井壁结构提供优化设计，对实际工程提出建设性意见，如调整配重水的注入量、控制井壁厚度、选择井壁材料等。
为更有效地组织现场施工，推广理论研究成果在实际工程中的应用，采用Python语言编写了计算流程，设定了判定循环逻辑。通过设置交互式对话框，输入基本计算参数(如钢筋、混凝土、泥浆、配重水的弹性模量和密度，井筒内外直径，当前井壁高度等)，计算当前最小配重水高度，井壁单位自重、配重水自重及井壁单位长度的浮力，截面刚度和临界深度，即可给出井壁结构稳定性的判定结论。部分源程序如下：
if Jg > a：
print(’井壁结构处于非稳定平衡状态’)
elif Jg == a:
print(’井壁结构处于稳定平衡临界状态’)
else:
print(’井壁结构处理稳定平衡状态’)
doc=open(’out.txt’,’a’,encoding=’utf-8’)
print(’##############’,file=doc)
print(’当前计算井深：{}m’.format(Jg),file=doc)
print(’按高度修正的井壁井弹性模量{}’.format(E1),file=doc)
print(’按高度修正的井壁井截面惯性矩{}’.format(I1),file=doc)
print(’最小配重水的高度：{}m’.format(Hw),file=doc)
print(’非满水状态下的钻井井壁竖向稳定临界深度：{}m’.format(a),file=doc)
print(’##############’,file=doc)
doc.close()
5 工程实例对比分析
5.1 工程背景
文献[1]中井筒深度H=300 m，外直径D=5.3 m，内直径d=4.6 m，井壁弹性模量E=3.3×109 kg/m2，截面惯性矩I=16.75 m4，单位长度井壁自重为pc=14.15×103kg/m，配重水自重pw=16.62×103kg/m，配重水最小高度Hw=222.4 m。
由式(18)求得满水状态下该井壁的临界深度为
由式(21)求得在非满水状态下井壁的临界深度为
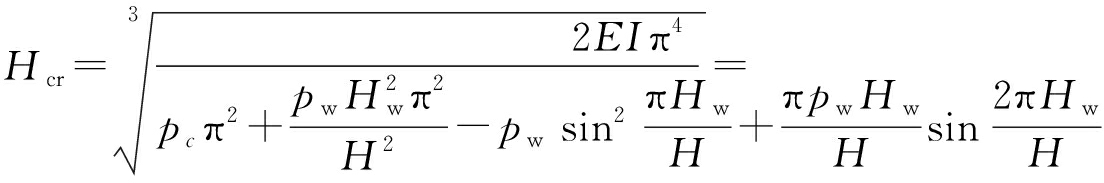
380.2 m
5.2 理论分析对比
将上述计算结果分别与文献[1，4]对比，得表1。从表1可以发现，该计算结果与文献[1](基于能量法的满水状态临界深度)计算结果相差0.396%，与文献[4](基于能量法的非满水状态临界深度)计算结果相差7.15%，吻合度较高。
表1 稳定性计算结果对比分析
Table 1 Comparative analysis of stability calculation results
来源公式表达式临界深度/m幅差/%式(18)Hcr=32π2EIpc+pw328.30文献[1]Hcr=3AEIq327.00.396式(21)Hcr=32EIπ4pcπ2+pwH2wπ2H2-pwsin2πHwH+πpwHwHsin2πHwH380.20文献[4]Hcr=3π2(EI1-EI2)π2α1-14sin 2πα1 +π2EI2 (q1-q2)π4α21+18π-18πcos 2πα1 +π4q211 000354.87.15
6 结 论
1)钻井井壁结构施工期竖向失稳是井壁结构平衡稳定状态由渐变到突变的变化过程，因此借助突变理论可以定量地分析井壁竖向失稳的机理，为钻井井壁稳定性研究提供一种新的理论分析方法。
2)基于等断面钻井井壁稳定性分析力学模型可求得井壁总势能函数，确立井壁失稳突变模型。以突变模型为依据，推导了满水和非满水状态下井壁竖向稳定临界深度计算公式，确立了井壁结构突变失稳判定准则。
3)为解决工程实际问题，更有效地指导现场施工，确立了井壁失稳计算的判定流程。借助大数据技术，由python语言编写了井壁稳定性计算流程。
4)通过工程实例计算及对比分析发现，基于突变理论的临界深度计算结果与能量法计算结果基本相同，从而验证了突变理论在钻井井壁稳定性理论研究中的可靠性。
[1] 洪伯潜.钻井法凿井深井井壁在泥浆中的轴向稳定[J].煤炭科学技术, 1980, 21 (9)：22-25.
HONG Boqian.Axial stability of deep drilling shaft lining in mud [J].Coal Science and Technology,1980,21(9):22-25.
[2] 洪伯潜.再论“钻井井壁在泥浆中的轴向稳定”[J].煤炭学报,2008,33(2):121-125.
HONG Boqian. Discussion vertical structural stability of a drilled shaft in mud further [J].Journal of China Coal Society,2008,33(2):121-125.
[3] 林鸿苞.钻井法凿井变断面井壁在泥浆中的竖向稳定[J].煤矿设计,1988(1):1-7.
LIN Hongbao.Vertical stability of variable cross-section drilling shaft lining in mud [J].Coal Engineering,1988(1):1-7.
[4] 张荣立,何国纬,李 铎.采矿工程设计手册[M].北京:煤炭工业出版社,1985.
[5] 牛学超,洪伯潜,杨仁树.充满配重水钻井井壁筒在泥浆中竖向结构稳定的理论研究[J].煤炭学报,2005,30(4):463-466.
NIU Xuechao,HONG Boqian,YANG Renshu. Theory study on axial structural stability of bored shafts filled with water[J].Journal of China Coal Society,2005,30(4):463-466.
[6] 牛学超,洪伯潜,杨仁树.非满配重水钻井井壁筒竖向结构稳定的理论研究[J].岩土力学,2006,27(11):1897-1901.
NIU Xuechao,HONG Boqian,YANG Renshu. Study on vertical structural stability of bored shafts filled part of water[J].Rock and Soil Mechanics,2006,27(11):1897-1901.
[7] 程 桦,刘吉敏,荣传新，等.变断面深厚表土钻井井壁竖向结构稳定性[J].煤炭学报,2008,33(12):1351-1357.
CHENG Hua,LIU Jimin,RONG Chuanxin,et al.Variable cross section shaft drilling lining’s vertical stability in thick alluvium[J].Journal of China Coal Society,2008,33(12):1351-1357.
[8] 荣传新,王 宇,刘吉敏，等.深厚表土层变断面钻井井壁竖向稳定临界深度的有限元计算[J].煤炭学报,2007,32(12):1277-1281.
RONG Chuanxin,WANG Yu,LIU Jimin,et al.Numerical simulation on vertical stability critical height of variable cross section drilling shaft in deep alluvium[J].Journal of China Coal Society,2007,32(12):1277-1281.
[9] 蒋万军.泥浆中超深钻井井壁竖向稳定研究[D].上海:同济大学,2008.
JIANG Wanjun.Study on vertical structural stability of super-deep bored shaft submerged in slurry[D].Shanghai:Tongji University,2008.
[10] 肖 立,张庆贺,蒋万军，等.泥浆中超深钻井井壁竖向稳定性分析[J].地下空间与工程学报,2009,5(S1):1325-1330.
XIAO Li,ZHANG Qinghe,JIANG Wanjun,et al.Study on vertical structural stability of a super-deep drilled shaft in slurry[J].Chinese Journal of Underground Space and Engineering,2009,5(S1):1325-1330.
[11] 王彦超,邓长根.钻井法施工阶段变刚度井壁结构整体稳定性分析[J].煤炭学报,2008,33(10):1152-1156.
WANG Yanchao,DENG Changgen.The effect of earth pressure on ground settlement after frozen soil thawing in connect aisle construction of metro engineering[J].Journal of China Coal Society,2008,33(10):1152-1156.
[12] 王彦超,邓长根.含初弯曲缺陷的变刚度井壁整体稳定性分析[J].东南大学学报(自然科学版),2009,39(1):68-72.
WANG Yanchao,DENG Changgen.Global stability analysis of bored shafts with initial bending imperfection and varying stiffness[J].Journal of Southeast University(Natural Science Edition)2009,39(1):68-72.
[13] 何 平,赵子都.突变理论及其应用[M].大连:大连理工大学出版社,1989.
HE Ping,ZHAO Zidu.Catastrophe theory and Its Application[M].Dalian:Dalian University of technology Press,1989.
[14] TIM Poston,IAN Stewart.Catastrophe theory and Its Application
(Dover Books on Mathematics)[M].USA:Dover Publications,2012.
[15] FASOULAKIS Z,AVRAAM T,RAFTOYIANNIS I.Dynamic buc-kling of partially-sway frames with varying stiffness using catastrophe theory[J].International Journal of Non-Linear Mechanics 2015,71,116-126.
[16] 穆成林,裴向军,路军富,等.基于尖点突变模型巷道层状围岩失稳机制及判据研究[J].煤炭学报,2017,42(6):1429-1435.
MU Chenglin,PEI Xiangjun, LU Junfu,et al.Study on the instability criterion of layered rock mass failure based on the cusp catastrophe theory[J].Journal of China Coal Society,2017,42(6):1429-1435.
[17] 周子涵,陈忠辉,包 敏,等.顺倾断续节理岩质边坡的稳定性突变研究[J].煤炭学报,2020,45(S1)：161-172.
ZHOU Zihan，CHEN Zhonghui，BAO Min,et al.Study on stability of rock slope with bedding intermittent joints based on catastrophe theory[J].Journal of China Coal Society,2020,45(S1)：161-172.
[18] 周子涵,陈忠辉,张凌凡,等.基于能量原理的露天矿边坡开挖稳定性突变研究[J].岩土力学,2019,40(12):4881-4889.
ZHOU Zihan,CHEN Zhonghui,ZHANG Lingfan,et al.Energy principle based catastrophe study of slope stability in open-pit excavation[J].Rock and Soil Mechanics,2019,40(12):4881-4889.
[19] 夏开宗,陈从新,刘秀敏,等.基于突变理论的石膏矿矿柱-护顶层支撑体系的破坏分析[J].岩石力学与工程学报,2016,35(S2):3837-3845.
XIA Kaizong,CHEN Congxin,LIU Xiumin,et al.Study of the failure of pillar-roof system in gypsum mines based on catastrophe theory[J].Chinese Journal of Rock Mechanics and Engineering,2016,35(S2):3837-3845.
[20] 夏开宗,陈从新,宋许根,等.相对湿度作用下的石膏矿护顶层突变破坏机制分析[J].岩土力学,2018,39(2):589-597.
XIA Kaizong,CHEN Congxin,SONG Xugen,et al.Analysis of catastrophic failure mechanism of roof bed in gypsum mines induced by relative humidity[J].Rock and Soil Mechanics,2018,39(2):589-597.
[21] 谢学斌,邓融宁,董宪久,等.基于突变和流变理论的采空区群系统稳定性[J].岩土力学,2018,39(6):1963-1972.
XIE Xuebin,DENG Rongning,DONG Xianjiu,et al.Analysis of catastrophic instability of plastic supporting system in old goaf of gypsum mine[J].Rock and Soil Mechanics,2018,39(6):1963-1972.
[22] 徐晓鼎,周跃进,庞 顺.石膏矿老采空区塑性支撑系统的突变失稳分析[J].岩石力学与工程学报,2018,37(11):2548-2555.
XU Xiaoding,ZHOU Yuejin,PANG Shun.Analysis of catastrophic instability of plastic supporting system in old goaf of gypsum mine[J].Chinese Journal of Rock Mechanics and Engineering, 2018,37(11):2548-2555.
[23] 刘鸿文.材料力学[M].北京:高等教育出版社,2011.
[24] 刘吉敏.配重水高度对钻井复合井壁竖向稳定性的影响[J].中国矿业,2012,21(S1):409-411.
LIU Jimin.The height of water’s influence on compound shaft drilling lining’s vertical stability[J].China Mining Magzine,2012,21(S1):409-411.
