Study on correlation of macro and microstructural parameters of hollowcylindrical grey sandstone based on PFC3D
-
摘要:
为从细观层面揭示主应力量值变化并为应力主轴旋转组合条件下围岩的破坏机理研究提供一种有效的数值模拟方法，基于空心圆柱灰砂岩单轴压缩和常规三轴压缩试验特性，分别采用单因素分析法、响应曲面分析法和回归分析法，研究了离散元软件PFC3D中平行黏结模型宏细观参数的敏感性特征。结果表明：依靠单因素分析法确定出的细观参数可靠性极低，基于响应曲面分析法和回归分析法获取的细观参数在低围压下与实验室结果表现出良好的拟合性；空心圆柱灰砂岩数值模型的抗压强度$ {\mathrm{\sigma }}_{\mathrm{c}} $与黏聚力$ \bar{c} $呈正相关；弹性模量$ E $分别与有效黏结模量$ {\bar{E}}_{{\mathrm{c}}} $、平行黏结刚度比的二次方（$ {\bar{k}}_{\mathrm{n}}/{\bar{k}}_{\mathrm{s}} $）2呈正相关，与$ {\bar{k}}_{\mathrm{n}}/{\bar{k}}_{\mathrm{s}} $呈负相关；泊松比v与平行黏结刚度比$ {\bar{k}}_{\mathrm{n}}/{\bar{k}}_{\mathrm{s}} $呈正相关；剪切裂纹比$ {\alpha } $与（$ {\bar{k}}_{\mathrm{n}}/{\bar{k}}_{\mathrm{s}} $）2呈线性相关。最后，采用迭代法对响应曲面分析法和回归分析法获取的细观参数进行了优化，优化后的数值模拟结果与实验室结果在不同围压下的试样峰值强度、变形参数和破坏形态方面吻合度较高。迭代法为PFC3D中平行黏结模型的细观参数标定提供了一种有效的方法，通过这一优化方法可以简化标定步骤，提升标定结果的适用性，提高模型的准确性和可靠性。
Abstract:In order to provide an effective numerical simulation method to reveal the damage mechanism study of surrounding rock under the combination of the change of principal stress value and the rotation of the stress principal axis from the fine-scale level, based on the uniaxial compression and conventional triaxial compression test characteristics of hollow cylindrical gray sandstone, the sensitivity of the macro fine-scale parameters of the parallel bonding model in the discrete element software PFC3D was studied by using the one-factor analysis method, the response surface analysis method, and the regression analysis method, respectively. characteristics of the parallel bonding model in the discrete element software PFC3D. The results show that: the reliability of the macroscopic parameters determined by the one-factor analysis method is extremely low, and the macroscopic parameters obtained based on the response surface analysis and regression analysis method show a good fit with the laboratory results at low perimeter pressure; the numerical model compressive strength $ {\sigma }_{\mathrm{c}} $ is positively correlated with cohesion $ \bar{c} $, and the elastic modulus E is positively correlated with the quadratic of the effective modulus of adhesion $ {\bar{E}}_{{\mathrm{c}}} $ and stiffness ratio $ {\bar{k}}_{\mathrm{n}}/{\bar{k}}_{\mathrm{s}} $, and positively correlated with stiffness ratio $ {\bar{k}}_{\mathrm{n}}/{\bar{k}}_{\mathrm{s}} $ positively correlated with the stiffness ratio $ {\bar{k}}_{\mathrm{n}}/{\bar{k}}_{\mathrm{s}} $ and negatively correlated with the quadratic of the stiffness ratio $ {\bar{k}}_{\mathrm{n}}/{\bar{k}}_{\mathrm{s}} $, Poisson's ratio v is positively correlated with the stiffness ratio $ {\bar{k}}_{\mathrm{n}}/{\bar{k}}_{\mathrm{s}} $, and the shear cracking ratio α is linearly correlated with the quadratic of the stiffness ratio $ {\bar{k}}_{\mathrm{n}}/{\bar{k}}_{\mathrm{s}} $. Finally, the fine-scale parameters obtained by response surface analysis and regression analysis were optimized using the iterative method, and the optimized numerical simulation results were in good agreement with the laboratory results in terms of the peak strength, deformation parameters and damage morphology of the specimens under different circumferential pressures. The iterative method provides an effective method for the calibration of the fine apparent parameters of the parallel bonding model in PFC3D, and this optimization can simplify the calibration steps, as well as enhance the applicability of the calibration results, and improve the accuracy and reliability of the model.
-
-
![]()
![]()
图 3 宏观力学参数与细观参数对应关系
Figure 3. Correspondence between macroscopic mechanical properties and fine parameters
![]()
图 4 基于单因素试验确定的细观参数数值模拟应力应变曲线与实验室结果对比
Figure 4. Comparison of numerically simulated stress-strain curves based on single-factor tests with laboratory results for fine-scale parameters
![]()
图 5 细观参数对宏观力学特性的响应曲面
Figure 5. Response surface of fine parameters to macroscopic mechanical properties
![]()
图 6 常规三轴压缩试验应力−应变曲线
Figure 6. Conventional triaxial compression test stress-strain curve
![]()
图 7 平行黏结摩擦角与宏观黏聚力和内摩擦角对应关系
Figure 7. Correspondence of parallel cohesive friction angle with macroscopic cohesion and internal friction angle
![]()
图 8 常规三轴压缩试验应力−应变曲线
Figure 8. Conventional triaxial compression test stress-strain curve
![]()
图 9 常规三轴压缩试验应力−应变曲线
Figure 9. Conventional triaxial compression test stress-strain curve
![]()
表 1 单因素试验分析法计算方案
Table 1 Calculation scheme of single-factor experimental analysis method
方案 $ {\bar{E}}_{\mathrm{c}} $/GPa $ {\bar{k}}_{\mathrm{n}}/{\bar{k}}_{\mathrm{s}} $ $ \bar{c} $/MPa k $ \bar{\varphi } $ 围压/MPa 1 8 2.9 10 0.7 12.5 0 2 10 2.9 10 0.7 12.5 0 3 12 2.9 10 0.7 12.5 0 4 14 2.9 10 0.7 12.5 0 5 10 1.0 20 0.7 12.5 0 6 10 2.5 20 0.7 12.5 0 7 10 2.0 20 0.7 12.5 0 8 10 3.0 20 0.7 12.5 0 9 10 2.9 20 0.7 12.5 0 10 10 2.9 30 0.7 12.5 0 11 10 2.9 40 0.7 12.5 0 12 10 2.9 50 0.7 12.5 0 13 10 2.9 20 0.7 10.0 0，5，10 14 10 2.9 20 0.7 20.0 0，5，10 15 10 2.9 20 0.7 30.0 0，5，10 16 10 2.9 20 0.7 40.0 0，5，10 
下载: 导出CSV
围压/MPa 抗压强度/MPa 弹性模量/GPa 泊松比 0 65.820 8.982 0.476 5 101.477 12.231 0.330 10 130.400 14.165 0.280 20 162.219 14.679 0.199
下载: 导出CSV
表 3 响应曲面试验设计
Table 3 Response surface experimental design
水平 −1 0 1 $ {\bar{E}}_{\mathrm{c}} $/GPa 9.00 10.50 12.00 $ \bar{{k}_{\mathrm{n}}}/\bar{{k}_{\mathrm{s}}} $ 2.00 2.50 4.00 $ \bar{c} $/MPa 35.00 40.00 45.00 $ \bar{{\varphi }} $/（°） 15.00 12.00 25.00
下载: 导出CSV
表 4 宏观参数及其主要影响因素
Table 4 Macro parameters and main influencing factors
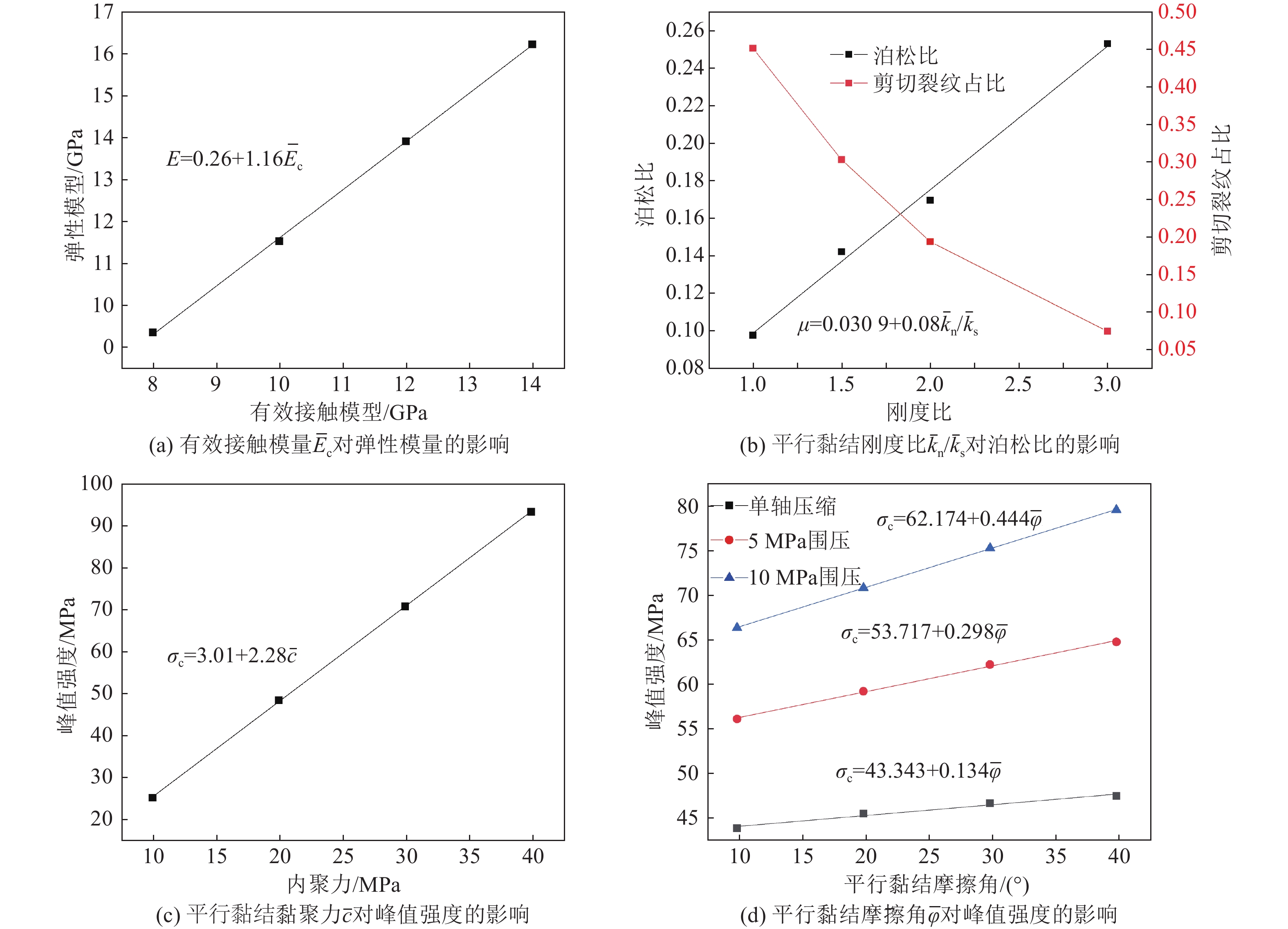
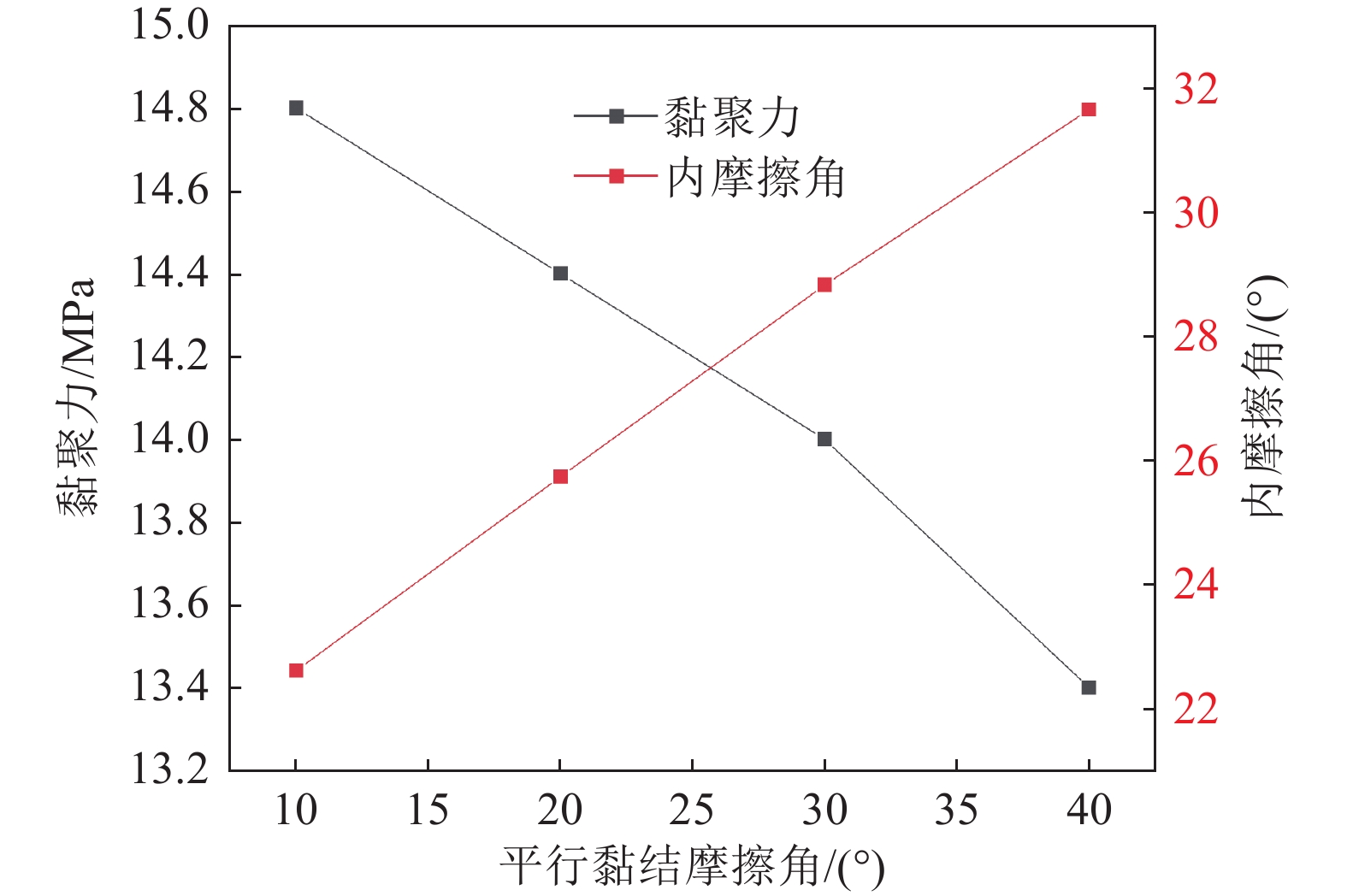
宏观参数 主要影响因素 抗压强度$ {\mathrm{\sigma }}_{\mathrm{c}} $ $ {\bar{k}}_{\mathrm{n}}/{\bar{k}}_{\mathrm{s}} $、$ \bar{c} $、$ {\bar{E}}_{c} $2、$ ({\bar{k}}_{\mathrm{n}}/{\bar{k}}_{\mathrm{s}}) $2、$ \bar{c} $2、$ \bar{\mathrm{\varphi }} $2 弹性模量E $ {\bar{E}}_{c} $、$ {\bar{k}}_{\mathrm{n}}/{\bar{k}}_{\mathrm{s}} $、$ {\bar{E}}_{c} $×$ {\bar{k}}_{\mathrm{n}}/{\bar{k}}_{\mathrm{s}} $、$( {\bar{k}}_{\mathrm{n}}/{\bar{k}}_{\mathrm{s}} )$2 泊松比$v $ $ \bar{{k}_{n}}/\bar{{k}_{s}} $ 剪切裂纹比$ \mathrm{\alpha } $ $ {\bar{k}}_{\mathrm{n}}/{\bar{k}}_{\mathrm{s}} $、$ \bar{c} $、$ \bar{\mathrm{\varphi }} $、$ {\bar{k}}_{\mathrm{n}}/{\bar{k}}_{\mathrm{s}} $×$ \bar{\mathrm{\varphi }} $、$ {\bar{E}}_{c} $2、$( {\bar{k}}_{\mathrm{n}}/{\bar{k}}_{\mathrm{s}}) $2、$ \bar{c} $2
下载: 导出CSV
表 5 灰砂岩宏细观参数之间回归关系式及拟合系数
Table 5 Table of regression equations and fitting coefficients between fine view parameters and macroscopic parameters of sandstone
编号 拟合公式 拟合系数 1 $ {\bar{E}}_{\mathrm{c}}=-3.443-0.013{\mathrm{\sigma }}_{\mathrm{c}}+0.876E+16.471v $ 0.987 2 $ {\bar{k}}_{\mathrm{n}}/{\bar{k}}_{\mathrm{s}}=0.788-0.008{\mathrm{\sigma }}_{\mathrm{c}}-0.004E+10.485v $ 0.994 3 $ \bar{c}=-6.267+0.408{\mathrm{\sigma }}_{\mathrm{c}}+28.719v $ 0.782 4 $ \bar{\varphi }=- $65.076$ + $3.312$ \varphi $ 0.999
下载: 导出CSV
表 6 试验1组细观参数更名及取值
Table 6 Name change and value of fine parameters of test group 1
细观参数 细观参数更名 细观参数取值 $ {\bar{E}}_{\mathrm{c}} $/GPa emodLast 11.579 $ {\bar{k}}_{\mathrm{n}}/{\bar{k}}_{\mathrm{s}} $ kratio 3.359 $ \bar{c} $/MPa cohLast 44.826 $ \bar{{\varphi }} $ faLast 23.460
下载: 导出CSV
表 7 实验室试验及试验1组试验结果
Table 7 Results of laboratory tests and test group 1 tests
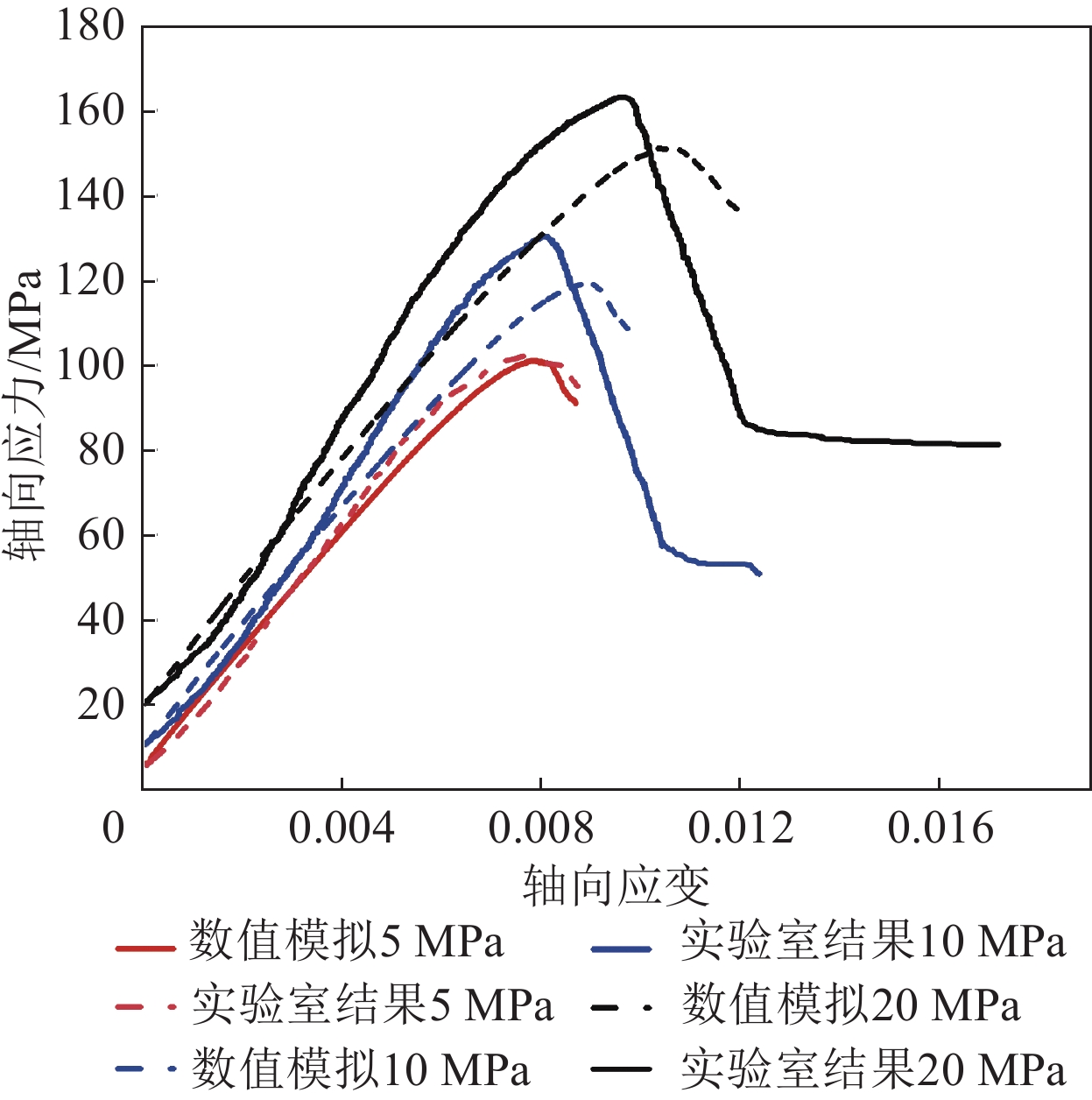
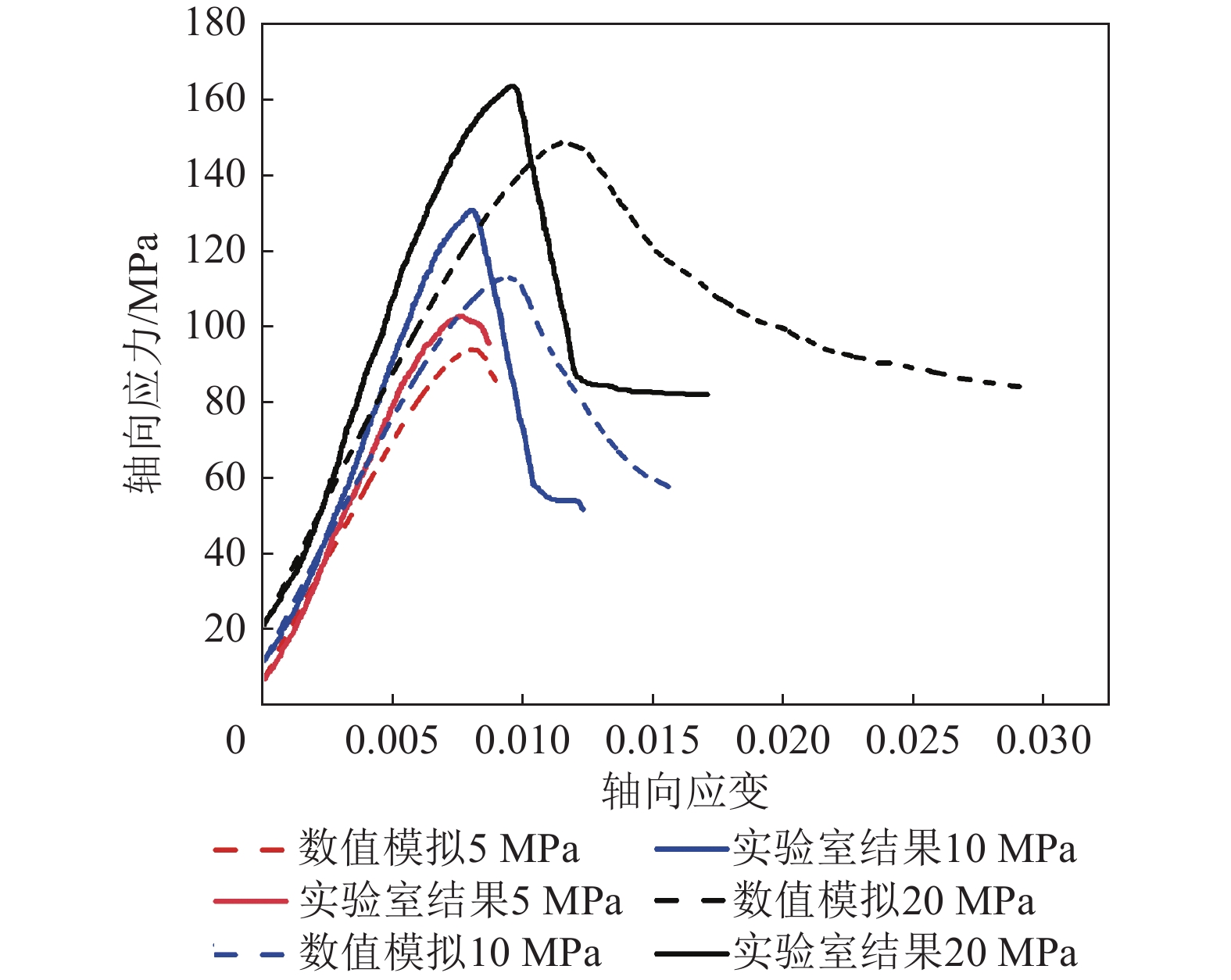
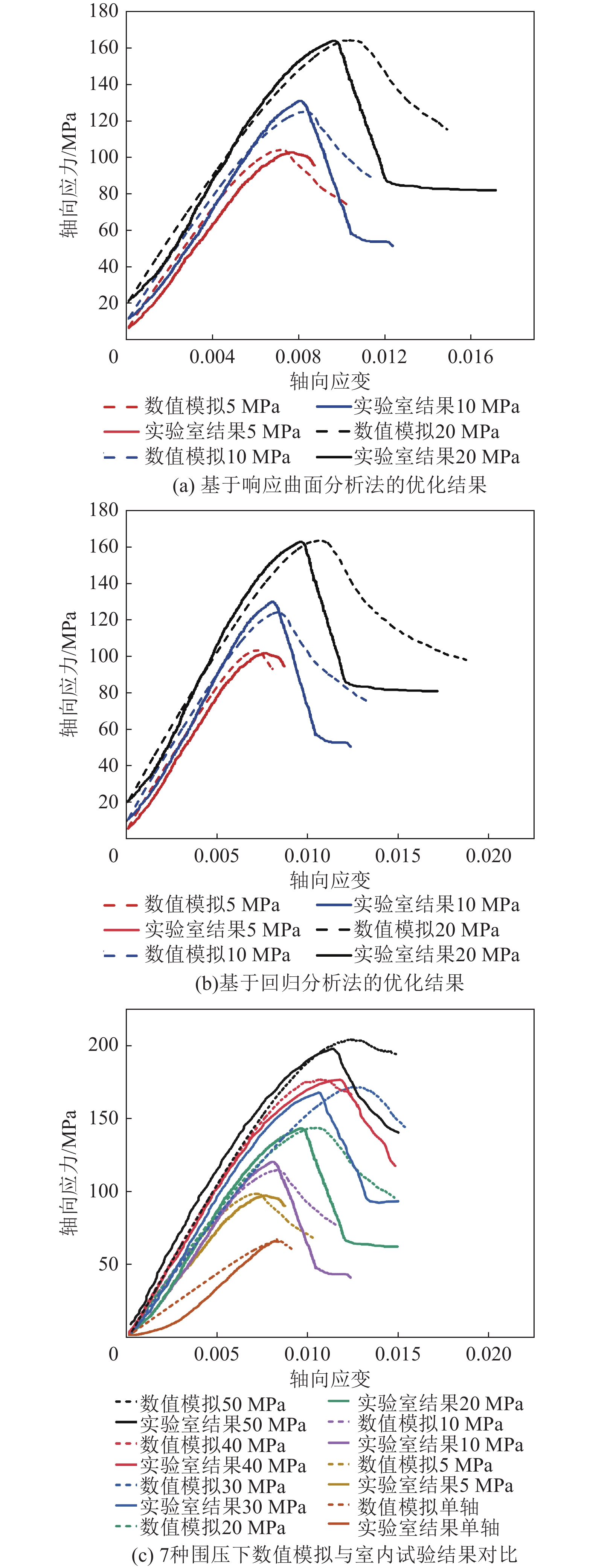
围压$ {P}_{i} $/MPa 抗压强度/MPa 轴向应变 室内试验结果$ {\sigma }_{i} $ 试验1组试验结果$ {\sigma }_{i}^{\prime} $ 室内试验结果$ {\varepsilon }_{i} $ 试验1组试验结果$ {\varepsilon }_{{i}}^{\prime}$ 5($ {P}_{1} $) 101.477($ {\sigma }_{1} $) 101.000($ {\sigma }_{1}^{\prime}$) 0.0078 ($ {\varepsilon }_{1} $)0.0082 ($ {\varepsilon }_{1}^{\prime} $)10($ {P}_{2} $) 130.400($ {\sigma }_{2} $) 119.140($ {\sigma }_{2}^{\prime} $) 0.0089 ($ {\varepsilon }_{2} $)0.0085 ($ {\varepsilon }_{2}^{\prime} $)20($ {P}_{3} $) 162.219($ {\sigma }_{3} $) 150.918($ {\sigma }_{3}^{\prime} $) 0.0103 ($ {\varepsilon }_{3} $)0.0097 ($ {\varepsilon }_{3}^{\prime} $)
下载: 导出CSV
-
[1] 周辉,黄磊,姜玥,等. 岩石空心圆柱扭剪仪研制的重点问题及研究进展[J]. 岩土力学,2018,39(12):4295−4304. ZHOU Hui,HUANG Lei,JIANG Yue,et al. Critical problems and research progress on the development of rock hollow cylinder torsional shear apparatus[J]. Rock and Soil Mechanics,2018,39(12):4295−4304.
[2] 伍永平,闫壮壮,罗生虎,等. 煤岩组合体应力传递与强度特征倾角效应[J]. 煤炭科学技术,2023,51(1):105−116. WU Yongping,YAN Zhuangzhuang,LUO Shenghu,et al. Dip effect of stress transfer and structural instability mechanism of coal-rock combination[J]. Coal Science and Technology,2023,51(1):105−116.
[3] LI Z,ZHOU H,JIANG Y,et al. Methodology for Establishing Comprehensive Stress Paths in Rocks During Hollow Cylinder Testing[J]. Rock Mechanics and Rock Engineering,2019,52(4):1055−1074.
[4] 张传庆,黄书岭,周 辉,等. 基于地应力水平评价的围岩潜在破坏模式研究[J]. 岩石力学与工程学报,2018,37(S1):3187−3195. ZHANG Chuanqing,HUANG Shuling,ZHOU Hui,et al. Study on potential failure modes of surrounding rock mass based on evaluation of geostress level[J]. Chinese Journal of Rock Mechanics and Engineering,2018,37(S1):3187−3195.
[5] 江权,史应恩,蔡美峰,等. 深部岩体大变形规律:金川二矿巷道变形与破坏现场综合观测研究[J]. 煤炭学报,2019,44(5):1337−1348. JIANG Quan,SHI Ying’en,CAI Meifeng,et al. In-situ observation on large deformation and failure of deep tunnel:Case study for the Jinchuan No. 2 Mine[J]. Journal of China Coal Society,2019,44(5):1337−1348.
[6] 姜玥,周辉,卢景景,等. 空心圆柱砂岩真三轴试验研究[J]. 岩土力学,2022,43(4):932−944. JIANG Yue,ZHOU Hui,LU Jingjing,et al. True triaxial test on hollow cylindrical sandstone[J]. Rock and Soil Mechanics,2022,43(4):932−944.
[7] JIANG Y,ZHOU H,LU J J,et al. Strength,deformation,and failure characteristics of hollow cylinder sandstone under axial–torsional tests[J]. Bulletin of Engineering Geology and the Environment,2023,82(8):296. doi: 10.1007/s10064-023-03295-0
[8] ZHOU H,JIANG Y,LU J J,et al. Development of a hollow cylinder torsional apparatus for rock[J]. Rock Mechanics and Rock Engineering,2018,51(12):3845−3852. doi: 10.1007/s00603-018-1563-5
[9] 刘超. 双应力主轴旋转条件下砂土扭剪试验研究[D]. 青岛:青岛理工大学,2022. LIU Chao. Experimental study on sand torsion shear under biaxial rotation of principal stress[D]. Qingdao:Qingdao Tehcnology University,2022.
[10] 滕越. 考虑主应力轴偏转效应的黏土卸荷力学特性研究[D]. 济南:济南大学,2022. TENG Yue. Study on unloading mechanical characteristics of clay considering the effect of principal stress deflection[D]. Jinan:University of Jinan,2022.
[11] 雷乐乐,王大雁,李栋伟,等. 考虑应力水平影响的冻结黏土变形特性[J]. 岩石力学与工程学报,2021,40(S1):2905-2912. LEI Lele,WANG Dayan,LI Dongwei,et al. Deformation characteristics of frozen clay with considering the influence of mean principal stress[J]. Chinese Journal of Rock Mechanics and Engineering,2021,40(S01):2905-2912.
[12] TALESNICK M L,RINGEL M. Completing the hollow cylinder methodology for testing of transversely isotropic rocks:torsion testing[J]. International Journal of Rock Mechanics and Mining Sciences,1999,36(5):627−639. doi: 10.1016/S0148-9062(99)00038-8
[13] LEE D H,JUANG C H,CHEN J W,et al. Stress paths and mechanical behavior of a sandstone in hollow cylinder tests[J]. International Journal of Rock Mechanics and Mining Sciences,1999,36(7):857−870. doi: 10.1016/S0148-9062(99)00063-7
[14] LEE D H,JUANG C H,LIN H M. Yield surface of mu-San sandstone by hollow cylinder tests[J]. Rock Mechanics and Rock Engineering,2002,35(3):205−216. doi: 10.1007/s00603-001-0023-8
[15] LEE D H,JUANG C H,LIN H M,et al. Mechanical behavior of Tien-Liao mudstone in hollow cylinder tests[J]. Canadian Geotechnical Journal,2002,39(3):744−756. doi: 10.1139/t02-014
[16] 周辉,姜玥,卢景景,等. 岩石空心圆柱扭剪仪试验能力[J]. 岩土力学,2018,39(5):1917−1922. ZHOU Hui,JIANG Yue,LU Jingjing,et al. Study of hollow cylinder torsional apparatus for rock[J]. Rock and Soil Mechanics,2018,39(5):1917−1922.
[17] 姜玥. 考虑应力主轴旋转的岩石力学特性试验研究[D]. 北京:中国科学院大学,2019 JIANG Yue. Experimental study on rock mechanical properties considering stress principal axis rotation[D]. Beijing:University of Chinese Academy of Sciences,2019.
[18] Itasca,C.G. PFC3D v5.0-user Manual. [EB/OL](2015-01-01)[2024-10-15]. https://xs.typicalgame.com/scholar?cluster=4170232382122427355&hl=en&as_sdt=2005&sciodt=0,5
[19] 朱焕春. PFC及其在矿山崩落开采研究中的应用[J]. 岩石力学与工程学报,2006,25(9):1927−1931. ZHU Huanchun. Pfc and application case of caving study[J]. Chinese Journal of Rock Mechanics and Engineering,2006,25(9):1927−1931.
[20] 杨艳,常晓林,周伟,等. 裂隙岩体水力劈裂的颗粒离散元数值模拟[J]. 四川大学学报(工程科学版),2012,44(5):78−85. YANG Yan,CHANG Xiaolin,ZHOU Wei,et al. Simulation of hydraulic fracturing of fractured rock mass by PFC2D[J]. Journal of Sichuan University (Engineering Science Edition),2012,44(5):78−85.
[21] 周文东,王笑然,陈力,等. 基于离散元模拟的受载裂隙岩体地震学声发射响应特征[J]. 煤炭科学技术,2024,52(10):54−62. ZHOU Wendong,WANG Xiaoran,CHEN Liran,et al. Seismological acoustic emission response characteristics of loaded fractured rock bodies based on discrete element simulation[J]. Coal Science and Technology,2024,52(10):54−62.
[22] 王海洋,李金浜,郑仕跃,等. 拉剪作用下椭圆孔洞砂岩力学及破坏特征模拟研究[J]. 煤炭科学技术,2023,51(8):86−96. WANG Haiyang,LI Jinbang,ZHENG Shiyue,et al. Simulation on mechanical and failure characteristics of sandstone with elliptical hole under tension-shear effect[J]. Coal Science and Technology,2023,51(8):86−96.
[23] 邓树新,郑永来,冯利坡,等. 试验设计法在硬岩PFC3D模型细观参数标定中的应用[J]. 岩土工程学报,2019,41(4):655−664. DENG Shuxin,ZHENG Yonglai,FENG Lipo,et al. Application of design of experiments in microscopic parameter calibration for hard rocks of PFC3D model[J]. Chinese Journal of Geotechnical Engineering,2019,41(4):655−664.
[24] 王晋伟,迟世春,邵晓泉,等. 正交–等值线法在堆石料细观参数标定中的应用[J]. 岩土工程学报,2020,42(10):1867−1875. WANG Jinwei,CHI Shichun,SHAO Xiaoquan,et al. Application of orthogonal-contour method in calibration of microscopic\r parameters of rockfill materials[J]. Chinese Journal of Geotechnical Engineering,2020,42(10):1867−1875.
[25] 郝保钦,张昌锁,王晨龙,等. 岩石PFC2D模型细观参数确定方法研究[J]. 煤炭科学技术,2022,50(4):132−141. HAO Baoqin,ZHANG Changsuo,WANG Chenlong,et al. Study on determination micro-parameters of rock PFC2D model[J]. Coal Science and Technology,2022,50(4):132−141.
[26] 郭鸿,王普,张科强,等. 离散元平行黏结模型的细观参数标定[J]. 中国科技论文,2019,14(6):610−613. GUO Hong,WANG Pu,ZHANG Keqiang,et al. Microscopic parameter calibration of parallel bonding model in DEM simulation[J]. China Sciencepaper,2019,14(6):610−613.
[27] 黄宜胜,夏晓丹. 砂岩颗粒流平行黏结模型细观参数标定方法研究[J]. 三峡大学学报(自然科学版),2021,43(4):7−12. HUANG Yisheng,XIA Xiaodan. Calibration method of mesoscopic parameters for parallel bonding model of sandstone particle flow[J]. Journal of China Three Gorges University (Natural Sciences),2021,43(4):7−12.
[28] 姜玥,周辉,卢景景,等. 不同应力路径下灰砂岩力学特性与强度参数研究[J]. 岩石力学与工程学报,2019,38(4):815−824. JIANG Yue,ZHOU Hui,LU Jingjing,et al. Study on mechanical properties and strength parameters of gray sandstone under different stress paths[J]. Chinese Journal of Rock Mechanics and Engineering,2019,38(4):815−824.
[29] 赵海军. 岩石单轴压缩试验离散元模拟分析[J]. 山西建筑,2018,44(11):72−73. ZHAO Haijun. Discrete element simulation analysis of rock uniaxial compression test[J]. Shanxi Architecture,2018,44(11):72−73.
[30] POTYONDY D O,CUNDALL P A. A bonded-particle model for rock[J]. International Journal of Rock Mechanics and Mining Sciences,2004,41(8):1329−1364. doi: 10.1016/j.ijrmms.2004.09.011
[31] 汪华安,焦春茂,陈晓. 基于颗粒流方法的滑坡机理数值分析[J]. 三峡大学学报(自然科学版),2020,42(1):47−51,112. WANG Hua’an,JIAO Chunmao,CHEN Xiao. Numerical analysis of landslide mechanism based on PFC2D[J]. Journal of China Three Gorges University (Natural Sciences),2020,42(1):47−51,112.
[32] 刘相如,杨圣奇. 基于正交试验的岩石细观力学参数数值研究[J]. 应用基础与工程科学学报,2018,26(4):918−928. LIU Xiangru,YANG Shengqi. Research on mesomechanical parameters of rock specimens based on orthogonal numerical tests[J]. Journal of Basic Science and Engineering,2018,26(4):918−928.
[33] 石崇,张强,王盛年. 颗粒流(PFC5.0)数值模拟技术及应用(第一版)[M]. 北京:中国建筑工业出版社,2021:262−278.
计量
- 文章访问数: 84
- HTML全文浏览量: 7
- PDF下载量: 61
